51nod 范德蒙矩阵

 

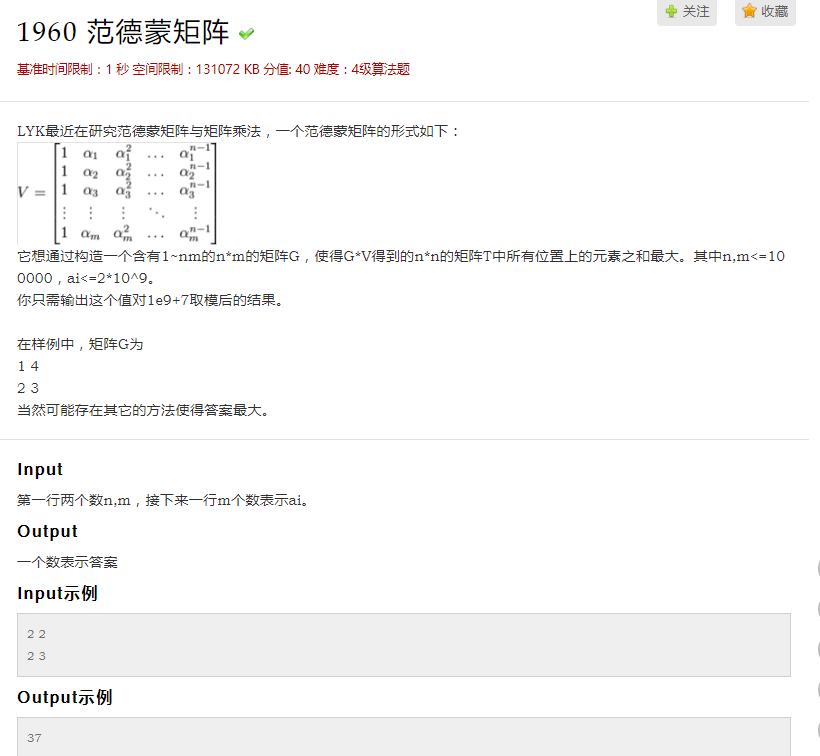
思路：　 根据矩阵乘法的定义，G中的第i行第j列的元素 ai,j ，对答案的贡献为 ai,j∗ T中第j行的所有元素之和。

　　　　因此我们可以将T中根据每行的和进行排序。第i行的和可以通过公式 (ai^n−1)/(ai−1)直接得出。
　　　　注意考虑 ai=1,ai=0 以及 ai>MOD 的特殊情况即可。还有就是对于除法取模需要用到逆元（费马小定理）

　　　　一开始没注意除法取模 狂WA 12遍也是心累。。。。。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>

using namespace std;
typedef long long LL;
const LL mod = 1e9 + 7;
const int maxn = 1e5 + 10;
LL b[maxn], ans, a[maxn];
LL n, m;
LL Pow(LL a, LL b)//快速幂
{
    LL ans = 1;
    while (b) {
        if (b & 1) {
            ans *= a;ans %= mod;
        }
        a *= a;a %= mod;
        b >>= 1;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    while (cin >> n >> m) {
        for (int i = 1; i <= m; i++) {
            cin >> a[i];
        }
        sort(a + 1, a + m + 1);
        for (int i = 1; i <= m; i++) {
            a[i] = (a[i] % mod + mod) % mod;
            if (a[i] == 0)b[i] = 1;
            else if (a[i] == 1)b[i] = n;
            else {                            //费马小定理对除法取模
                b[i] = (Pow(a[i], n) - 1 + mod) % mod;
                b[i] = b[i] * Pow(a[i] - 1, mod - 2) % mod;
            }
        }
        //以下是求解
        ans = 0;
        LL num = (n*(n + 1) / 2) % mod;
        for (int i = 1; i <= m; i++) {
            ans = (ans + (num*b[i]) % mod) % mod;
            num = (num + n * n) % mod;
        }
        cout << ans << endl;
    }
    return 0;
}