2024.6.6

所学时间：2.2小时

代码行数：62

博客园数：1篇

所学知识：今天学习了工程数学的Newton法程序设计。

掌握Hesse矩阵的计算方法和Newton法的基本思想及其迭代步骤；学会运用MATLAB编程实现常用优化算法；能够正确处理实验数据和分析实验结果及调试程序。

实验内容

（1）求解无约束优化问题：；

（2）终止准则取；

（3）完成Newton法（牛顿法）的MATLAB编程、调试；

（4）选取几个与实验二中相同的初始点，并给出相关实验结果的对比及分析（从最优解、最优值、收敛速度（迭代次数）等方面进行比较）；

（5）按照模板撰写实验报告，要求规范整洁。

算法步骤、代码、及结果

1. 算法步骤

(1).初始化变量 x 为初始猜测。

(2).设置迭代停止条件 epsilon，即迭代过程中的步长小于该值时停止迭代。

(3).进入迭代循环，直到满足停止条件为止。

(4).在每次迭代中，计算目标函数关于变量 x 的梯度和海森矩阵。

(5).根据梯度和海森矩阵计算更新步长 step，使用线性方程求解方法求解方程 ( H \Delta x = \nabla f )，其中 ( H ) 是海森矩阵，( \nabla f ) 是目标函数的梯度。

(6).更新变量 x，即 ( x = x - \Delta x )。

(7).计算目标函数的值 f_val。

(8).输出当前迭代次数、更新后的变量 x 和目标函数值 f_val。

(9).如果更新步长 step 的范数小于设定的停止条件 epsilon，则满足停止条件，跳出循环。

2. 代码

function newtons_method()

    % 初始猜测

    x = [1; 1; 1; 1];

    % 设定迭代停止条件

    epsilon = 1e-6;

    % 迭代

    iter = 0;

    while true

        % 计算梯度和海森矩阵

        grad = [2*(x(1)+10*x(2))+40*(x(1)-x(4))^3; 20*(x(1)+10*x(2))+4*(x(2)-2*x(3))^3; 10*(x(3)-x(4))-8*(x(2)-2*x(3))^3; -10*(x(3)-x(4))-40*(x(1)-x(4))^3];

        hessian = [2+120*(x(1)-x(4))^2, 20, 0, -120*(x(1)-x(4))^2; 20, 200+12*(x(2)-2*x(3))^2, -24*(x(2)-2*x(3))^2, 0; 0, -24*(x(2)-2*x(3))^2, 10+48*(x(2)-2*x(3))^2, -10; -120*(x(1)-x(4))^2, 0, -10, 10+120*(x(1)-x(4))^2];

        % 计算步长

        step = hessian\grad;

        % 更新解

        x = x - step;

        % 计算目标函数值

        f_val = (x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4;

        % 输出迭代信息

        disp(['迭代次数： ', num2str(iter), ': x = ', num2str(x'), ', f(x) = ', num2str(f_val)]);

        % 判断是否满足停止条件

        if norm(step) < epsilon

            disp(['最优解 x = ', num2str(x'), ', 最优值f(x) = ', num2str(f_val)]);

            break;

        end

        iter = iter + 1;

    end

    disp(['共迭代:',num2str(iter),'次']);

end

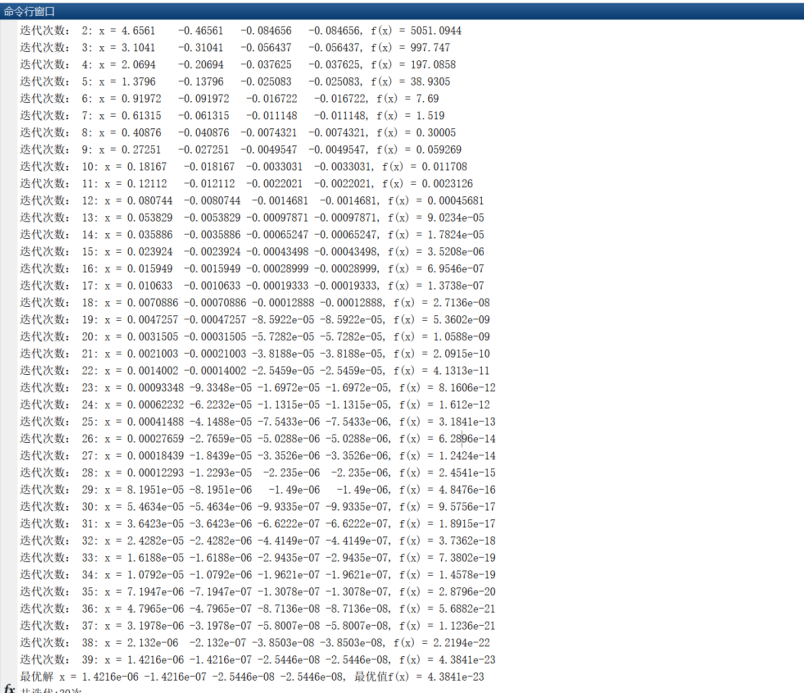
3. 结果