2024.5.29

所学时间：3.5小时

代码行数：162

博客园数：1篇

所学知识：今天学习了工程数学的黄金分割法实验

一、实验目的

通过一维寻优黄金分割法的程序设计，培养学生计算机的应用能力，并为今后无约束优化方法的学习和编程，奠定基础；掌握缩小寻优区间的黄金分割法。

二、实验内容

（1）请用0.618法求解优化问题：

 

的极小点和极小值（进退法确定初始区间），精度为10^-6；

（2）根据0.618法算法步骤编写Matlab的程序实现0.618搜索法；

（3）要求输出内容包括：极小点、极小值、每次迭代的a、b、a_l、a_k的值；

（4）按照模板撰写实验报告，要求规范整洁。

三、算法步骤、代码、及结果

1. 算法步骤

(1)初始化参数 t=(sqrt(5)-1)/2 和变量 h=b-a，计算 phia=phi(a) 和 phib=phi(b)。

(2)计算左试探点 p=a+(1-t)h 和右试探点 q=a+th，分别计算 phip=phi(p) 和 phiq=phi(q)。

(3)初始化迭代次数 k=1，将当前区间 [a,b] 和试探点 p、q 存入矩阵 G 中。

(4)进入循环，当区间长度 h 大于给定精度 delta 时执行以下步骤： a. 若 phip 小于 phiq，则更新区间右端点 b=q、phib=phiq、q=p，并重新计算试探点 p 和 phip。 b. 否则更新区间左端点 a=p、phia=phip、p=q，并重新计算试探点 q 和 phiq。 c. 更新区间长度 h=b-a。

(5)将更新后的区间 [a,b] 和试探点 p、q 存入矩阵 G 中，迭代次数 k 自增 1。

(6)当循环结束时，计算最终步长 ds=abs(b-a) 和最终函数值差值 dphi=abs(phib-phia)。

(7)比较 phip 和 phiq，选择较小的函数值作为最终的最优解 s 和对应的函数值 phis。

(8)返回最优解 s、最优函数值 phis、迭代过程的区间信息矩阵 G、最终步长和函数值差值组成的向量 E。

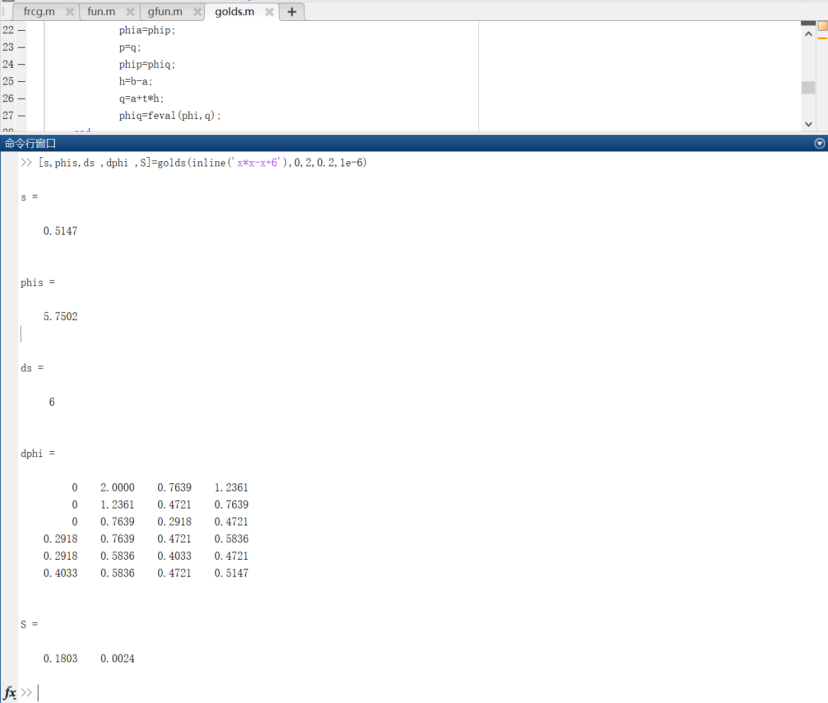
2. 代码

function [s,phis,k,G,E]=golds(phi,a,b,delta,epsilon)

t=(sqrt(5)-1)/2;

h=b-a;

phia=feval(phi,a);phib=feval(phi,b);

p=a+(1-t)*h;%左试探点

q=a+t*h;%右试探点

phip=feval(phi,p);

phiq=feval(phi,q);

k=1;

G(k,:)=[a,b,p,q];

while(h>delta)

    if(phip<phiq)

            b=q;

            phib=phiq;

            q=p;

            phiq=phip;

            h=b-a;

            p=a+(1-t)*h;

            phip=feval(phi,p);

    else

            a=p;

            phia=phip;

            p=q;

            phip=phiq;

            h=b-a;

            q=a+t*h;

            phiq=feval(phi,q);

    end

    k=k+1;

    G(k,:)=[a,b,p,q];

end

ds=abs(b-a);dphi=abs(phib-phia);

if(phip<=phiq)

    s=p;phis=phip;

else

    s=q;phis=phiq;

end

E=[ds,dphi];