无向连通图图求割点与割边

割点：

概念：

割点：在一个无相连通图中，如果删除某个顶点后，图不再连接（即任意两点之间不再相互到达），我们称这样的顶点为割点（或者称为割顶）。

思考：

很容易想到的方法是：以此删除每个顶点，然后用深度优先搜索或者广度优先搜索来检查图是否依然连通。如果删除某个顶点后，，导致图不再联通，那么刚才删除的顶点就是割点，但是这种方法复杂度太高，所以需要换一种方法；

首相我们从图中的任意顶点开始对图进行遍历，我们在遍历的时候一定会遇到割点（废话），关键是如何确认一个顶点是割点。

假如我们深度优先遍历事访问到了k点，此时图就会被k点分成两部分。一部分是已经被访问过的点，另一部分是没有被访问过的点。如果k点事割点，那么剩下的没有被访问过点中至少会有一个点在不经过k点的情况下，是无论如何再也回不到已访问过得点了，那么一个连通图就是被k点分割成了不连通的子图；

这个算法的关键在于：当深度优先遍历访问到顶点u时，假设图中还有顶点v是没有访问过的点，如何判断顶点v在不经过顶点u的情况下是否还能回到之前访问过的任意一个点？如果从生成树的角度来说，顶点u就是顶点v的父亲，顶点v就是顶点u的儿子，而之前已经被访问过的顶点就是祖先。换句话说，如何检测顶点v在经过父节点u的情况下还能否回到祖先。我们的放大是对顶点v再进行一次深度优先遍历，但是此次遍历时不允许经过顶点u，看看还能否回到祖先。如果不能回到祖先则说明顶点u是割点。

例如以下例子：

 

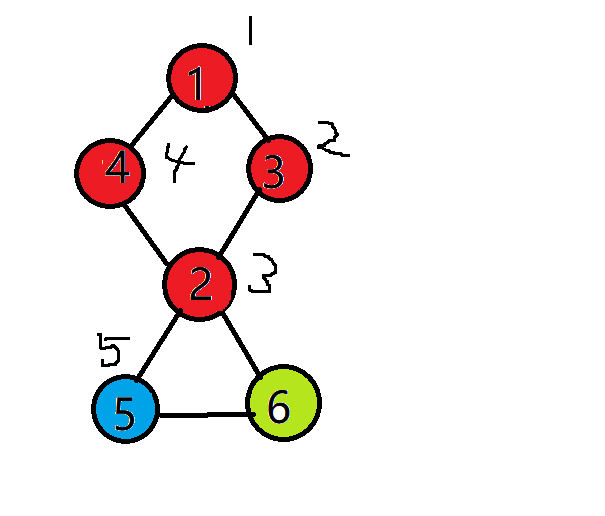
上图是深度优先遍历访问到5号顶点的时候，图中只剩下6号顶点还没有被访问过。现在6号顶点在不经过5号顶点的情况下，可以回到之前被访问过得顶点有1,3,2和4号顶点。我们这里只需要他能够回到最早顶点的“时间戳”（即tarjan算法中的low[ ]数组）。对于6号顶点来说就是记录1，因为6号顶点能够回到的最早顶点是1号顶点，而1号顶点的时间戳为1（圆圈右上方的数）。为了不重复计算，我们用low[ ]数组来记录每个顶点在不经过父顶点时，能够回到的最小的“时间戳”：

 

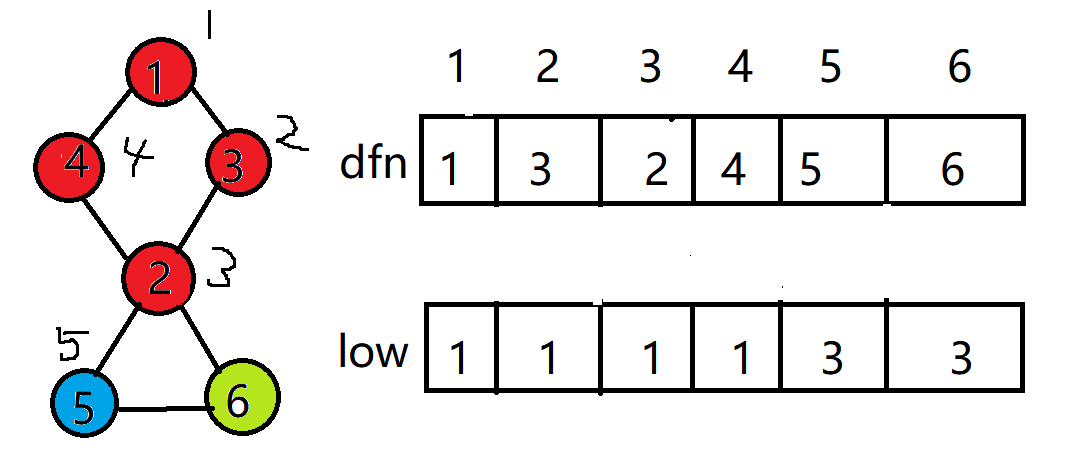
 对于某个顶点u，如果存在至少一个顶点v（即顶点u 的儿子），使得low[v]>=dfn[u]，即不能回到祖先，那么u点为割点。对于本例们

号顶点的儿子只有6号顶点，且low[6]的值为1，而5号顶点的时间戳dfn[5]为5，low[6]<dfn[5]，可以回到祖先，因此5号顶点不是割点。2号顶点是时间戳dfn[2]为3，他的儿子5号顶点的low[5]为3，low[5]==dfn[3],表示5号顶点不能绕过2号顶点从而访问到更早的祖先，因此2号顶点是割点；

代码实现：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
int n,m;
struct link
{
    int to;
    int next;
}edge[maxn];
int head[maxn],tot;
int dfn[maxn],low[maxn];
bool flag[maxn];
int root=1;
int cnt;
inline void add(int x,int y)
{
    edge[++tot].to =y;
    edge[tot].next = head[x];
    head[x] = tot;
} 
void tarjan(int u,int father)
{
    low[u] = dfn[u] = ++cnt;
    int child = 0;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v])
        {
            child++;
            tarjan(v,u);
            low[u] = min(low[u],low[v]);
            if(u!=root&&low[v]>=dfn[u])
            {
                flag[u] =true;
            }
            if(u==root&&child==2)
            {
                flag[u] =true;
            }
        }else if(v!=father)
        {
            low[u] = min(low[u],dfn[v]);
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
    }
    tarjan(1,root);
    for(int i=1;i<=n;i++)
    {
        if(flag[i]==true)
        {
            printf("%d ",i);
        }
    }
    return 0;
}

割边：

概念：

割边（也叫桥）：在一个无向图中，如果删除某条边后，图不再联通。

思考：

求割边，只需将求割点的算法修改一个符号。只需将low[v]>=dfn[u]改为low[v]>dfn[u]，取消一个等于号即可。low[v]>=dfn[u]带边的是点v是不可能在不经过父亲节点u而回到祖先（包括父亲），所以顶点u是割点。如果low[v]和dfn[u]相等则便是还可以回到父亲，而low[v]>dfn[u]则表示连父亲都回不到了。倘若顶点v不能回到祖先，也没有另外一条边能回到父亲，那么u-v这条边就是割边。

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
int n,m;
struct link
{
    int to;
    int next;
}edge[maxn];
int head[maxn],tot;
int dfn[maxn],low[maxn];
bool flag[maxn];
int root=1;
int cnt;
inline void add(int x,int y)
{
    edge[++tot].to =y;
    edge[tot].next = head[x];
    head[x] = tot;
} 
void tarjan(int u,int father)
{
    low[u] = dfn[u] = ++cnt;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u] = min(low[u],low[v]);
            if(low[v]>dfn[u])
            {
                printf("%d --- %d\n",u,v);
            }
        }else if(v!=father)
        {
            low[u] = min(low[u],dfn[v]);
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
    }
    tarjan(1,root);
    return 0;
}

 

注：以上思路取自：《啊哈算法》

以上；