[论文阅读笔记] Fast Network Embedding Enhancement via High Order Proximity Approximati
[论文阅读笔记] Fast Network Embedding Enhancement via High Order Proximity Approximation
本文结构
- 解决问题
- 主要贡献
- 主要内容
- 参考文献
(1) 解决问题
大多数先前的工作,要么是没有考虑到网络的高阶相似度(如谱聚类,DeepWalk,LINE,Node2Vec),要么是考虑了但却使得算法效率很低,不能拓展到大规模网络(如GraRep)。
(2) 主要贡献
Contribution 1. 将许多现有的NRL算法架构总结成一个统一的框架(相似度矩阵构造以及降维),并且得出一个结论,如果更高阶的相似度信息被考虑进相似度矩阵,那么NRL算法的表征效果会提高。
Contribution 2. 提出了NEU增强策略来提高现有的NRL算法的表征效果,经由NEU算法处理过的表征矩阵R在理论上融入了节点的更高阶相似度(近似)。最后,在多标签分类和链路预测实验上证明了算法不仅在时间上是有效的,而且在精度上也是有很大提升的。
(3) 主要内容
1. 预备知识
- K阶相似度: 一阶相似度可以表示为两节点的边权,二阶相似度可以表示为两节点的公共邻居数,那么推广到更高阶的相似度呢?首先考虑二阶相似度的另一种解释:节点vi走两步到达节点vj的概率。将一阶二阶相似度简单推广到k阶相似度,即节点vi走k步到达节点vj的概率。 假设A为归一化后的邻接矩阵(一阶相似度转移概率矩阵),那么k阶相似度转移概率矩阵为Ak(k阶相似度转移矩阵),Akij表示节点vi走k步到达节点vj的概率。
(个人理解: 高阶相似度为什么会起作用?由于现实中的网络往往都是稀疏的,这意味着边的规模和节点的规模往往是一样的。因此,真实网络的一阶相似度矩阵通常是非常稀疏的,仅凭一阶相似度已不足以反应节点间的关系。因此,需要结合更高阶的节点相似度)
2. 统一框架
论文提出了一个基于相似度矩阵的降维(矩阵分解)的统一框架,并将现有算法归结到该框架中。
基于相似度矩阵的降维(矩阵分解)统一框架包含两个步骤:
- Step 1:相似度矩阵M的构造。(如邻接矩阵,拉普拉斯矩阵,k阶相似度矩阵等)
- Step 2:相似度矩阵的降维,即矩阵分解,如特征值分解或SVD分解。
目标: 分解矩阵 M=RCT,即寻找矩阵R和矩阵C来似矩阵M,矩阵M和矩阵RCT的离可以用差的矩阵范数来表。其中,R为中心向量表征矩,C为上下文向量表征矩阵。
举例说明算法符合上述统一框架:
Example 1:Spectral Clustering(SC)
相似度矩阵M:归一化后的拉普拉斯矩阵(一阶相似度)
降维方法:特征值分解。
Example 2:Graph Factorization (GF)
相似度矩阵M:归一化后的邻接矩阵(一阶相似度)降维方法:SCD分解。
Example 3:DeepWalk
相似度矩阵M:
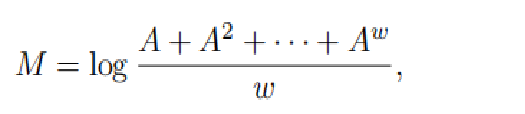
DeepWalk算法以基于随机游走生成的采样来近似高阶相似度,而没有实际上去精确计算k阶相似度矩阵。
降维方法:以目标函数优化的方式,SkipGram的目标优化(SGD),寻找矩阵R和矩阵C使得RCT近似M。
Example 4:GraRep
算法原理:
GraRep精确计算1,...k阶,k个相似度矩阵,并且为每个相似度矩阵计算一个特定的表 征(利用SVD分解),最后将这k个表征连接起来。
本质上也是基于相似度矩阵分解,属于提出的统一框架但是,GraRep不能有效适用于大规模网络,计算效率太低。
3. 算法原理
根据以上算法存在的问题:本论文研究如何从近似高阶相似度矩阵中有效的学习网络表征(使得算法既有效率又有效果)。
假设我们已经用上述NRL框架中的某个算法学习了相对比较低阶的相似度矩阵f(A)的近似RCT。在这个基础之上,我们的目标是去学习一个更好的R'和C',其R'C'T近似一个更高阶的矩阵g(A),其度比f(A)更高。
f(A)的定义(相似度矩阵):表示由A的1...k次幂组成的多项式。f(A)的度k表示多项式中考虑到的最大阶的相似度,即A的最大次幂,参考以上DeepWalk的相似度矩阵,f(A)=M。
注意到NEU算法主要是为了增强其他表示学习模型得到的嵌入结果,即在含有低阶信息的嵌入向量的基础上,融合更高阶的信息生成质量更好的嵌入向量。该算法原理很简单,即对其他算法得到的表示向量嵌入矩阵做一个后处理操作,其迭代更新公式如下:
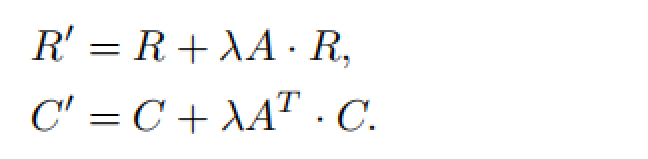
一个疑问:这个R和C的迭代更新是怎么考虑进了更高阶的相似度的?
Theorem:
给定网络表征矩阵R和向下文向量表征矩阵C(可由其他表征算法学习而得),假设RCT近似相似度矩阵M=f(A),近似误差限

且f(A)的度为K。经由上述迭代公式(3)更新而得的R’和C’的积R’C’T近似于矩阵

g(A)具有K+2的度,且近似误差限为

由以上定理可以得出结论: 即每迭代更新一次,分解的近似相似度矩阵的度提升2,但是相应的误差上限会提升2.25倍,因此必须权衡融入的高阶节点相似度信息以及相应的误差。
一个变种的迭代公式:
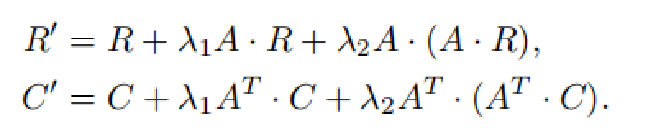
可以推得变种迭代更新公式在一次迭代中可以获得更高阶的相似度(第一个迭代公式一次迭代只是多了2阶)。(当然比变种迭代公式更复杂的在一次迭代中获得更高阶的相似度的迭代公式可以类似推广)
总结:说了那么多就是对其他表示学习算法得到的嵌入矩阵进行以上迭代更新,即可在嵌入向量中融入更高阶的信息。
(4) 参考文献
Yang C , Sun M , Liu Z , et al. Fast Network Embedding Enhancement via High Order Proximity Approximation[C]// International Joint Conference on Artificial Intelligence. AAAI Press, 2017.



