Pytorch_第七篇_深度学习 (DeepLearning) 基础 [3]---梯度下降
深度学习 (DeepLearning) 基础 [3]---梯度下降法
Introduce
在上一篇“深度学习 (DeepLearning) 基础 [2]---神经网络常用的损失函数”中我们介绍了神经网络常用的损失函数。本文将继续学习深度学习的基础知识,主要涉及基于梯度下降的一类优化算法。首先介绍梯度下降法的主要思想,其次介绍批量梯度下降、随机梯度下降以及小批量梯度下降(mini-batch)的主要区别。
以下均为个人学习笔记,若有错误望指出。
梯度下降法
主要思想:沿着梯度反方向更新相关参数,使得代价函数逐步逼近最小值。
思路历程:
假设给我们一个损失函数,我们怎么利用梯度下降法找到函数的最小值呢(换一种说法,即如何找到使得函数最小的参数x)?首先,我们应该先清楚函数的最小值一般位于哪里。按我的理解应该是在导数为0的极值点,然而极值点又不一定都是最小值点,可能是局部极小值点。那么,既然知道了最小值点在某个极值点(梯度为0),那么我们使得损失函数怎么逼近这个极值点呢?
现在我们反过来思考上述梯度下降法的主要思想。首先,要理解这个主要思想,我们需要理解梯度方向是什么。梯度方向指的是曲面当前点方向导数最大值的方向(指向函数值增大的方向)。假设我们现在处在函数上x=xt这个点(梯度不为0,不是极值点),因此现在我们需要确定增加x还是减少x能帮忙我们逼近函数的最小值。前面说过梯度方向指向函数值增大的方向,因此我们只要往梯度的反方向更新x,就能找到极小值点。(可能还是有点迷,下面结合例子具体看梯度下降的执行过程来理解其主要思想)
(note: 由于凸函没有局部极小值,因此梯度下降法可以有效找到全局最小值,对于非凸函数,梯度下降法可能陷入局部极小值。)
举个梨子:
假设有一个损失函数如下(当x=0的时候取得最小值,我们称x=0为最优解):
我们需要利用梯度下降法更新参数x的值使得损失函数y达到最小值。首先我们随机初始化参数x,假设我们初始化参数x的值为xt,如下图所示:
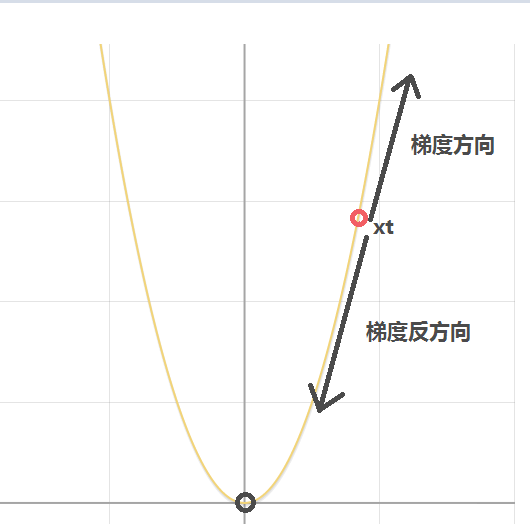
现在问题转化为我们怎么更新参数x的值(当前为xt)使得其越来越靠近使得函数达到最小值的最优参数x。直观上看我们需要减小x的值,才能使得其越来越靠近最优参数。
现在我们求取y对参数x的导(当有多个参数时,为偏导),如下:
由于xt>0,因此当我们代入xt到y',我们可以发现在点xt处导数(梯度)为正值,所指方向为图中所示的梯度方向。很明显,我们不能随着梯度指示的方向更新参数x,而应该往梯度方向的负方向更新。如上图所示,很明显,应该减小x的值才能慢慢靠近最优解。因此,不难给出参数x的更新公式(即梯度下降的参数一般更新公式)如下(α为学习率):
我们来验证上述更新公式。
- 当x=xt(xt>0)(位于y轴右边),则在x处的导数也大于0,由更新公式,下一时刻的x会减少(如上图所示x=xt减少会越来越靠近最优解x=0)。
- 当x=-xt(xt>0)(位于y轴左边),则在x处的导数也小于0,代入更新公式,我们发现下一时刻x会增加(如上图所示x=-xt增加会越来越靠近最优解x=0)。因此推导出的梯度下降参数更新公式符合我们的目标。
- 因此不断对参数x对上述更新,最终x的值会慢慢靠近最优解x=0.
上述便是梯度下降法的原理了,只不过举的例子比较简单,多参数(如神经网络中的参数w和b)的可以类似推理。
一个注意点:假设我们现在处在x=xt这个点,若学习率α设置过大,虽然收敛速度可能会加快(每次跨步大),但是xt也可能会过度更新,即(一次性减得太多)可能会越过最优解(跑到最优解的左边),再一次更新的话也可能会再次越过最优解(一次性加得太多,跑到最优解的右边),emmm,就这样反复横跳,始终达不到最优解。另外,学习率设置太小的话,x虽然更可能达到最优解,但是算法收敛太慢(x的每一个跨步太短)。对于学习率的选择,可以按0.001、0.01、0.1、1.0这样子来筛选。
现在依次介绍三种类型的梯度下降法,批量梯度下降、随机梯度下降以及小批量梯度下降。 以下介绍均以Logistic回归模型的损失函数(凸函数)为例,如下:
其中input = (x1,x2)为输入的训练样本。我们的目标是在训练样本集(假设有N个训练样本)上寻找最优参数w1、w2以及b使得损失函数在训练样本上达到最小的损失。(神经网络的训练过程过程就是输入训练样本,计算损失,损失函数反向对待更新参数求梯度,其次按照梯度下降法的参数更新公式朝着梯度反方向更新所有参数,如此往复,直到找到使得损失最小的最优参数或者达到最大迭代次数)(注意到损失函数上还有一个常量n我们没有解释,其实我觉得以下三个基于梯度下降的优化算法主要区别就是在n的取值上)
批量梯度下降(n=N的情况)
对于上述问题,批量梯度下降的做法是什么样的呢?其每次将整个训练样本集都输入神经网络模型,然后对每个训练样本都求得一个损失,对N个损失加权求和取平均,然后对待更新参数求导数,其次按照梯度下降法的参数更新公式朝着梯度反方向更新所有参数。通俗来讲就是每次更新参数都用到了所有训练样本(等价于上述损失公式中的n=N)。每一轮参数更新中,每个训练样本对参数更新都有贡献(每一个样本都给了参数更新一定的指导信息),因此理论上每一轮参数更新提供的信息是很丰富的,参数更新的幅度也是比较大的,使得参数更新能在少数几轮迭代中就达到收敛(对于凸优化问题能达到全局最优)。然而,对于大数据时代,训练样本可能有很多很多,每轮都是用那么多的样本进行参数更新的指导的话,更新一次(一次epoch)会非常非常久,这是这种方法的主要缺点。
随机梯度下降(n=1的情况)
对于上述优化问题,随机梯度下降(SGD)与批量梯度下降法的主要区别就是, SGD每一轮参数更新都只用一个训练样本来指导参数更新(n=1)。也就是说每次只计算出了某训练样本的损失,并进行反向传播指导参数更新。其优点是每一轮迭代的时间开销非常低(因为只用到了一个训练样本)。然而一个训练样本提供的信息可能比较局限,即其可能使得某次参数更新方向并不是朝着全局最优的方向(如噪声样本提供的信息可能就是错误的,导致其往偏离全局最优的方向更新),但是整体上是朝着全局最优的方向的。虽然随机梯度下降可能最终只能达到全局最优附近的某个值,但是相对于批量梯度下降来说最好的地方就是速度很快,因此基于精度和效率权衡,更常用的还是SGD。
小批量(mini-batch)梯度下降(n=num_batch)
小批量梯度下降是上述两种方法的一个折中,即既考虑精度也考虑了收敛速度。那么折中方法是怎么做的呢?首先小批量梯度需要设置一个批量的大小(假设是num_batch),然后每次选取一个批量的训练样本,计算得到num_batch个损失,求和取平均后反向传播来指导参数更新(n=num_batch)。通俗来说就是每一轮的参数更新我们既不是用上整个训练样本集(时间开销大),也不是只用一个训练样本(可能提供错误信息),我们是使用一个小批量的样本(1<n<N)来指导参数更新。虽然可能效果没有批量梯度下降法好,速度没有随机梯度下降法快,但是这种方法在精度和收敛速度上是一个很好的折中。因此,在深度学习中,用得比较多的一般还是小批量(mini-batch)梯度下降。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号