LINE学习
LINE
Abstract
LINE 是一种将大规模网络结点表征成低维向量的算法,可很方便用于网络可视化,结点分类,链路预测,推荐。
source code
Advantage
LINE相比于其他算法来说有如下几点优势:
- 适用于大规模网络。
- 有明确的目标函数(这一点DEEPWALK是没有的,DW没有提出一个明确的目标函数来告知什么网络属性被保留下来,直观上讲,DW更偏向于结点间有更高的二阶相似度的有相似的表征)该目标函数既反映了局部结构又反映了全局结构。LINE同时考虑了一阶相似度和二阶相似度
- 局部结构:顶点间的一阶相似性(由观察到的顶点间的链接强度表示,链接强度大的两结点有相似的向量表示,不足以反映图的全局结构,因此引入二阶相似度)
- 全局结构:顶点间的二阶相似性(由顶点间的共享邻域来决定,具有共享邻居的结点更可能是相似的)
用一张图来直观理解
关联图中6,7结点的是一条强边,因此结点6,7的向量表示应该相似(一阶相似度);而结点5,6因为共享了相似的邻居,因此5,6的向量表示也应该相似(二阶相似度)。
- 提出一种新颖的边采样的方法解决了随机梯度下降算法的局限性。(由于现实网络中边权的方差往往是非常大的,SGD可能导致梯度爆炸,损害性能)
ps:具体措施:以正比于边权大小的概率来采样边,将被采样的边作为二值边(0 无边,1有边)进行模型更新。
在这种采样过程中,目标函数保持不变,边的权重不再影响梯度。
- LINE可适用于任何类型的网络:有向无向,有权无权(DW只能适用于无权网络)
Definition
- 一阶相似度:两个结点u,v之间的边权代表u与v之间的一阶相似度。若u,v之间无边,则一阶相似度为0.

- 二阶相似度:两个结点u,v的二阶相似度由两个结点共同邻居的个数决定。

Model Description
LINE with First-order Proximity
首先,了解一下KL散度和一阶相似度的概念
KL散度Dkl(p,q):指用q分布来近似p分布的信息损失。
一阶相似度:对于两个有边链接的顶点,其边的强度越大,则该两顶点关系越密切,即越相似。
模型大体过程:
- 首先计算两个结点的联合概率密度

- 其次计算两结点经验分布概率
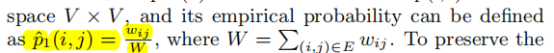
- 最小化下列目标函数
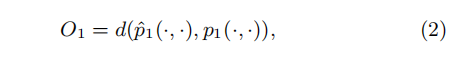
这里的d,两个分布的距离可以用KL散度来计算,最终目标函数如下:
即对图中每条边,计算相关联两顶点的kl散度,求各个结点向量表示ui,使得该目标函数达到最小。
(个人理解PS:但是为什么使得联合概率分布近似经验分布的信息损失最小就是保留一阶相似度?经验分布,边权除以边权总和一定程度上体现了边权的重要性,而边权的大小又是描绘一阶相似度的重要信息,因此可以将该经验分布理解成保留了一阶相似度的分布,而求各个结点的向量表示,使得两节点的联合分布近似于经验分布的信息损失最小,即该组向量表示就是体现一阶相似度的最优的向量表示)
上述一阶相似度只适用于无向图,而不适用于有向图。
LINE with Second-order Proximity
首先要理解二阶相似度的相关概念
- 二阶相似度既适用于有向图也适用于无向图。
- 二阶相似度即指,有相同上下文(邻居)的顶点越相似。
模型大体过程
- 首先,每个顶点由两个向量表示,ui表示该顶点i本身的向量表示,当顶点i被当做是其他顶点的上下文来考虑时,ui’为其向量表示。
- 其次计算在顶点i出现的条件下,下一个顶点是j的概率(条件概率)
 利用该公式,我们可以算出顶点i的条件分布,即
利用该公式,我们可以算出顶点i的条件分布,即 。
。
因此 根据二阶相似度的定义,我们不难推出,具有相似条件分布的顶点彼此相似。 - 因此,类似于一阶相似度,为了更好保留二阶相似度,我们需要使得每个结点i的条件分布近似于自身条件经验分布的信息损失最小。即最小化下述目标函数
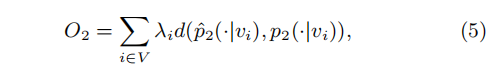 其中:
其中:
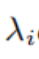
为每个结点在网络中的权重(考虑到每个结点在网络中的重要性可能不同)。该权重可以通过度来衡量,或者一些算法来计算,比如PageRank算法。- 条件经验分布如下计算

- 最后仍然使用kl散度来衡量两分布的距离。
最终目标函数如下:

通过学习每个结点i的两个向量表示ui,ui’来最小化上述目标函数,最终可以得到每个结点的向量表示。
Combining first-order and second-order proximities
那么如何同时结合一阶相似度和二阶相似度呢?这篇论文提出时涉及了两种方案:
- 分别训练基于一阶相似度的和基于二阶相似度的,得到每个结点的两种向量表示,
再连接该两种向量表示。 - 同时优化两个目标函数(3)和(6)来学习向量表示。留待未来研究。
Model Optimization
ps:个人对这部分理解不够成熟,可能有误。
优化上述目标函数(6)需要很大的计算开销(需要对每一条边进行采样来训练模型)。这里使用负采样来解决问题。
- Optimization via Edge Sampling
负采样:根据一定的策略选取部分更重要的边来进行训练,每次训练只对神经网络的部分权重进行更新,大大减少了SGD过程中的计算量。
(ps:正比于边的权重作为概率进行边的采样。一般来说,边权越大的应该被采样的概率要越高,在语言学领域:出现单词对频率越高的应该被采样的概率越大)
上述这种边采样策略提高了随机梯度下降的效率。
- 时间复杂度
LINE 时间复杂度是边的线性函数,与顶点个数V无关。如下:
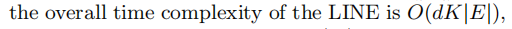
Discussion
1. 低度顶点的嵌入表示
由于低度顶点邻居数目极少,原网络中提供的信息有限,尤其在基于二阶相似度的LINE算法中是非常依赖于顶点的邻居数目的,那么如何确定低度顶点的向量表示呢?
一种直观的方法:添加更高阶的邻居(如邻居的邻居)来作为该低度结点的直接邻居。 与新添邻居边的权重如下:
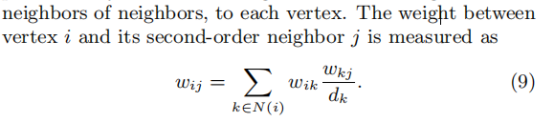
dk是结点k的出边的权重总和。(实际上,可以只添加与低度顶点i有边的,且边权最大的顶点j的邻居作为顶点i的二阶邻居)
2. 如何找到网络中新添加顶点的向量表示
如果已知新添加的顶点i与现有顶点的联系(即存在边),则可得到其经验分布
之后通过最小化目标函数(3)或(6)可得到新加顶点i的向量表示

如果未能观察到新添顶点与其他现有顶点的联系,我们只能求助其他信息,比如顶点的文本信息,留待以后研究。
6.Conclusion
LINE 适用于大规模网络;既保留了一阶相似度,又保留了二阶相似度;提出边采样算法,只采样部分且只更新神经网络部分权值,并且将采样的边处理成二进制边,解决了加权边梯度下降的局限性(即梯度爆炸----边权直接乘以梯度,且若边权方差过大 可能导致梯度爆炸),加快了效率。
未来的拓展:一阶二阶以外更高阶的相似度以及在异构网络中的应用。






