Fibnacci数列递归实现

Fibnacci数列递归实现

什么Fibnacci数列

通过查阅斐波那契数列，其中，它是这么说的：

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

总结而言，斐波那契数列从第三项开始，每一项的值都是前两项的和。

递归表达式

def fib(n):
 return 1 and n <= 2 or fib(n - 1) +fib(n - 2)
print('%d'%(fib(10)))

python实现结果

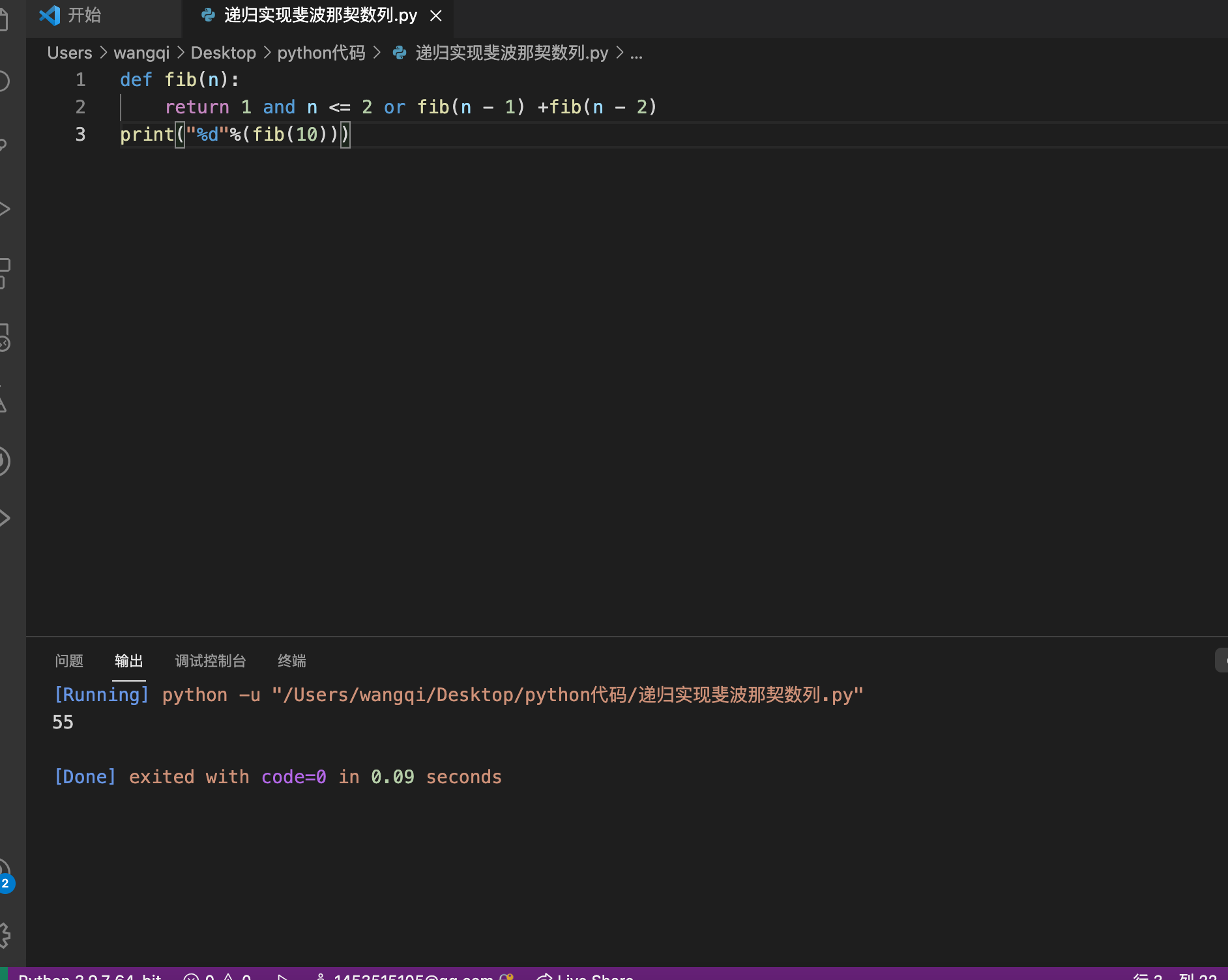
尝试fib(100)、fib(1000)、fib(10000)

在尝试fib(100)的时候，我就放弃了，因为运行了好一会儿都没有运行出结果。100尚且如此，何况后面的大数字，我害怕把我的电脑搞崩，就强制停止了程序运行，自然肯定没有一分钟以内运行出结果了。

解决问题

以上是通过递归算法实现的斐波那契数列的运算，还有种是用非递归的方法，参考了Fibonacci数列的递归与非递归实现以及python 入门之斐波那契数列递归表达式算法和非递归算法
其中，第二篇博客中指出：

总结为什么使用递归方式实现算法很长时间算不出来的原因：
(1) 递归算法时间复杂度为：O(2^N）----太耗时间
(2) 非递归算法时间和空间复杂度都为：O(N)

代码如下：

def fib(n):
    last = 1
    now = 1
    fibnext = 1
    for i in range(n):
        if i < 2:
            fibnext = 1
        else:
            fibnext = last + now
            last = now 
            now = fibnext
    return fibnext

print("%d"%(fib(10000)))    #或fib(100)或fib(1000)

运行结果如下：

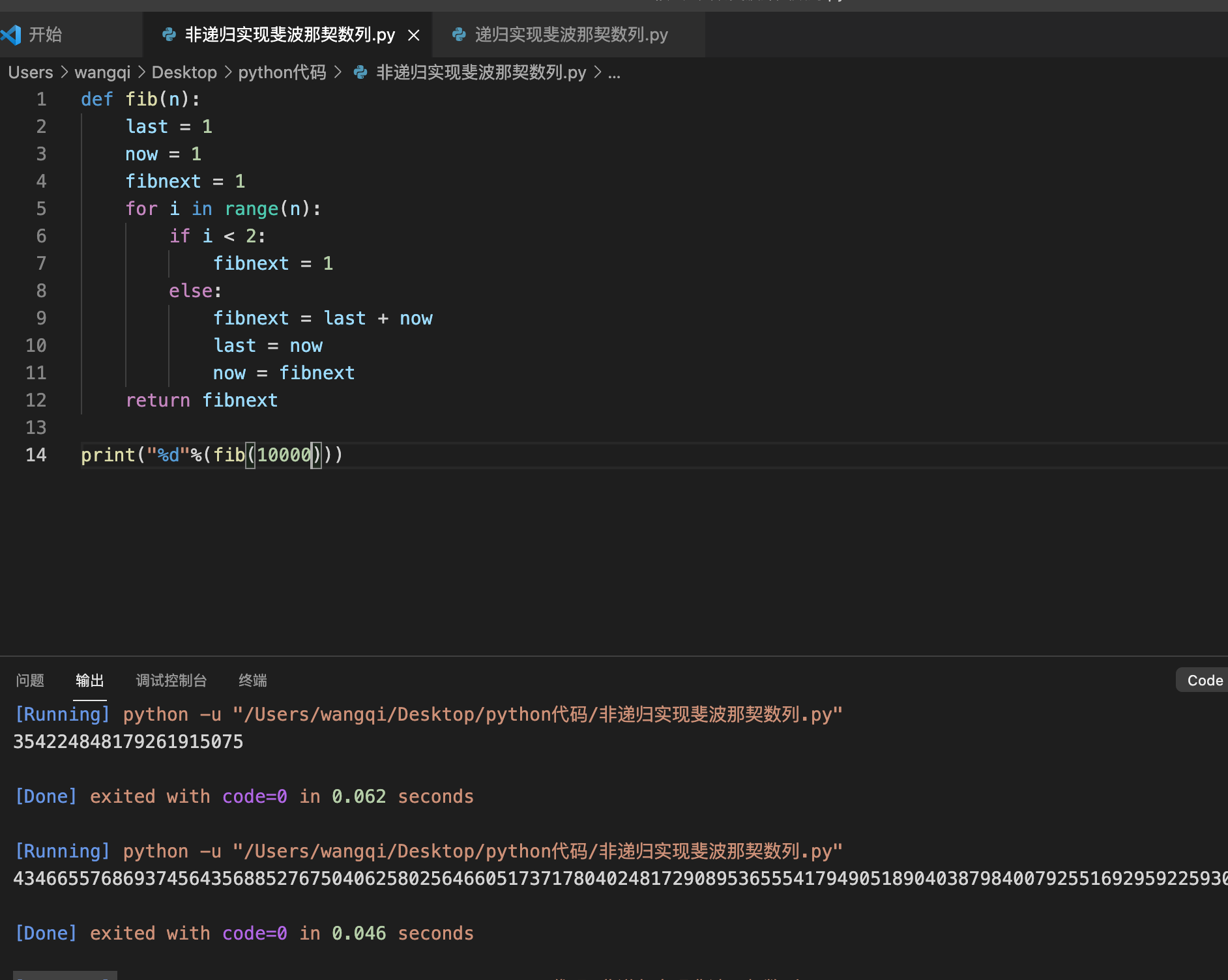
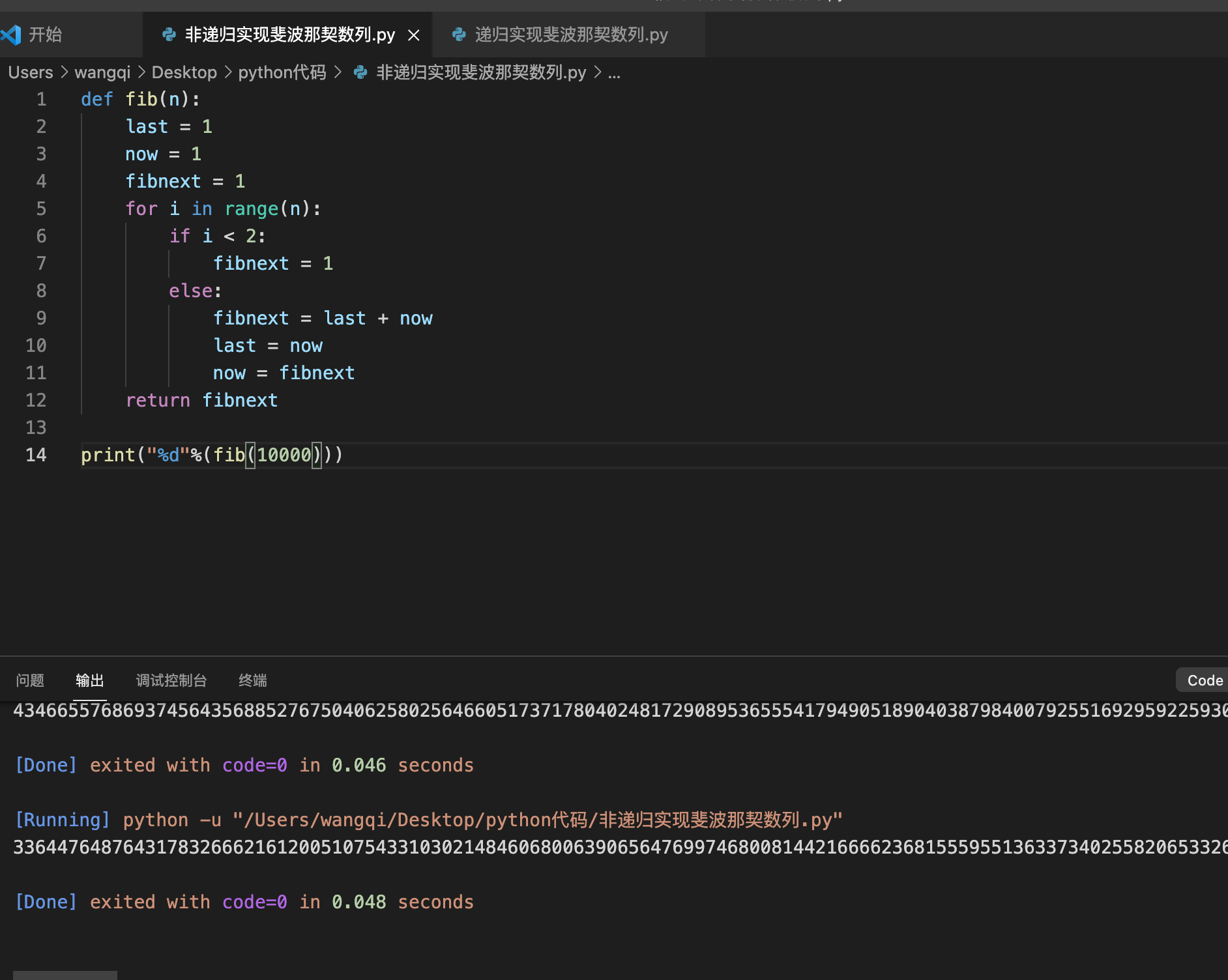
可以看到运行速度非常快，几乎是电光火石之间。