2021-2022-1 学号 20211408 《信息安全专业导论》第四周学习总结

2021-2022-1 学号 20211408 《信息安全专业导论》第四周学习总结

作业信息

2020-2021-1信息安全专业导论
2020-2021-1信息安全专业导论第四周作业
BASE64编码、IEEE754 浮点数、罗马数字转阿拉伯数字

教材学习内容总结

教材

感觉门和电路里的六种门的类型和python里的逻辑运算符还有位运算符有相通之处，这些逻辑运算感觉的符号的表示方式和数学的运算也有相通之处，我认为可以放在一起比较记忆，借助各自概念更好理解。布尔代数的性质也和数学代数运算还有集合的运算有相通处。教材的这一章节我阅读的速度也是比以往要慢，需要更多时间消化、理解。感觉收获很大，书上的逻辑框图走了一遍，留下了比较深的印象，也对芯片的一些原理有了些许了解，如集成电路容纳了许多门，需要很多引脚等。其中：

非门

将输入的电平以相反的方式输出，输入1，输出0；输入0，输出1
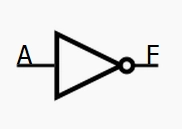X=A'
我感觉它与数学上的逆命题、python的逻辑非（not）类似，可以放在一起记忆

与门

针对两个信号，只有当输入信号都是1的时候输出才为1，否则为0
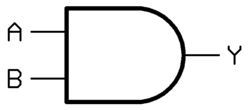X=A·B
我感觉它与数学上的乘法（比如0乘以任何一个数都为0）、python的逻辑与（and）类似，可以放在一起记忆

或门

同样针对两个信号，只有当输入信号都是0的时候才输出为0，否则为1
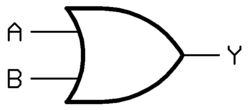X=A+B
我感觉它与数学上的加法（从真值表中可以看出，1+0=1，0+0=0等）、python的逻辑或（or）有些类似，可以放在一起记忆

异或门

针对两个信号，只有两个输入值相同时输出为0，否则为1
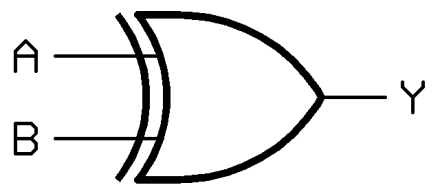X=A⊕B
定义比较好记忆，相比于或门，输出信号都是1的时候，或门输出是1，异或门输出为0，其中A⊕B=A·B'+A'·B

与非门

与门的输出值取逆
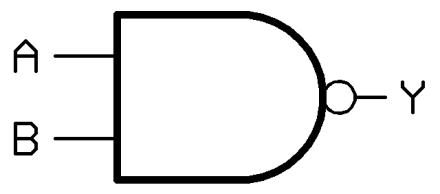X=(A·B)'
理解与门，与非门就好理解。

或非门

或门的输出取逆
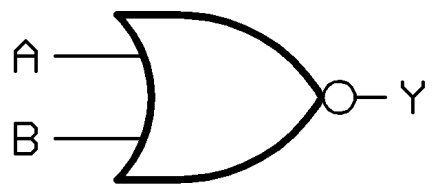X=(A+B)'
也是十分好理解。

可以有两个以上的输入的门，构成比较复杂的门，之后构成电路，完成一定任务。

门的构造

通过晶体管的连接来构造门，晶体管由半导体制成，通常用硅制作。

晶体管构造门

非门	与非门	或非门

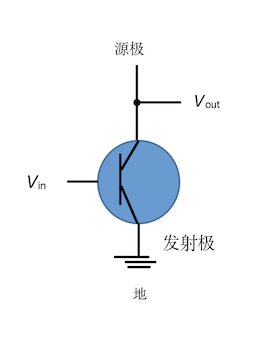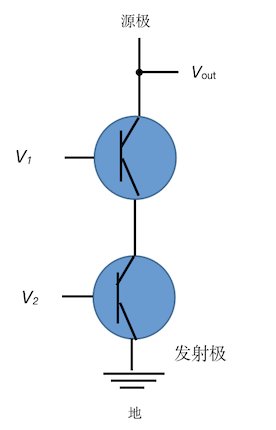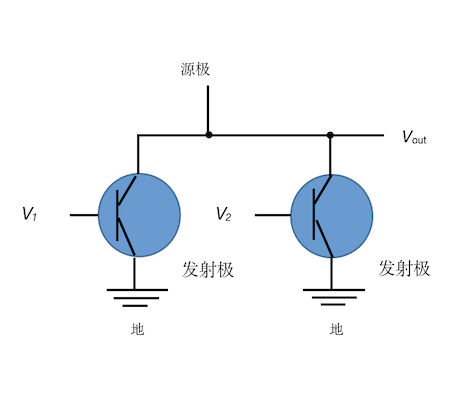如图，接地信号会转变为0伏，按非门所示，若输入信号为1，则因接地而变为0输出；若是0，则不接地输出为1。后两者与串联电路和并联电路有类似之处，我认为可以放一起比较记忆。与非门二者串联，有一个为1，输出即为1；两个都为0，不接地输出为1，两个都为1，接地输出为0。或非门并联，只要有一个为1，输出为0，二者都为0时输出才为1。

组和电路

一些性质：

性质	与	或
交换律	AB = BA	A + B = B + A
结合律	(AB)C = A(BC)	( A + B ) + C = A + ( B + C )
分配律	A(B+C) = (AB) + (AC)	A + (BC) = ( A + B )( A + C )
恒等	A1 = A	A + 0 = A
补	A(A') = 0	A + (A)' = 1
德·摩根定律	(AB)' = A' OR B'	( A + B )' = A'B'

其中，德·摩根定律我认为和集合运算有相通之处，可以放在一起比较记忆。

加法器

只能计算两个数位的和，不能计算多于两个位数的和，需要用到全加器，两个半加器可以构成一个全加器
和 = A⊕B（异或门）
进位 = AB（与门）

多路复用器的输出值为多个输入值之一，也就是只有一个输出值（n条线路中决定2^{n个输出值，决定其中一个输出）；而多路分配器相反，只有一个输入，n条控制线输出2}n个输出

存储器电路

存储信息的电路构成时序电路

S-R锁存器

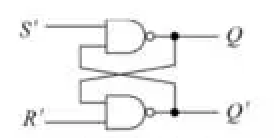
S和R是1的情况下可以进行保存数据，将S和R中任意一个暂时设置为0，X会根据运算逻辑变成你想存储的数据，也就是1或0，变成了以后迅速恢复S或R至1，也就完成了存储数据的操作，而那些大的数据就需要在此基础之上扩展这样的电路。

集成电路

集合了很多门电路，边缘有引脚。

CPU芯片

一种具有输入线和输出线的高级电路。

base64

学习了base64的编码，主要根据百度百科进行学习。
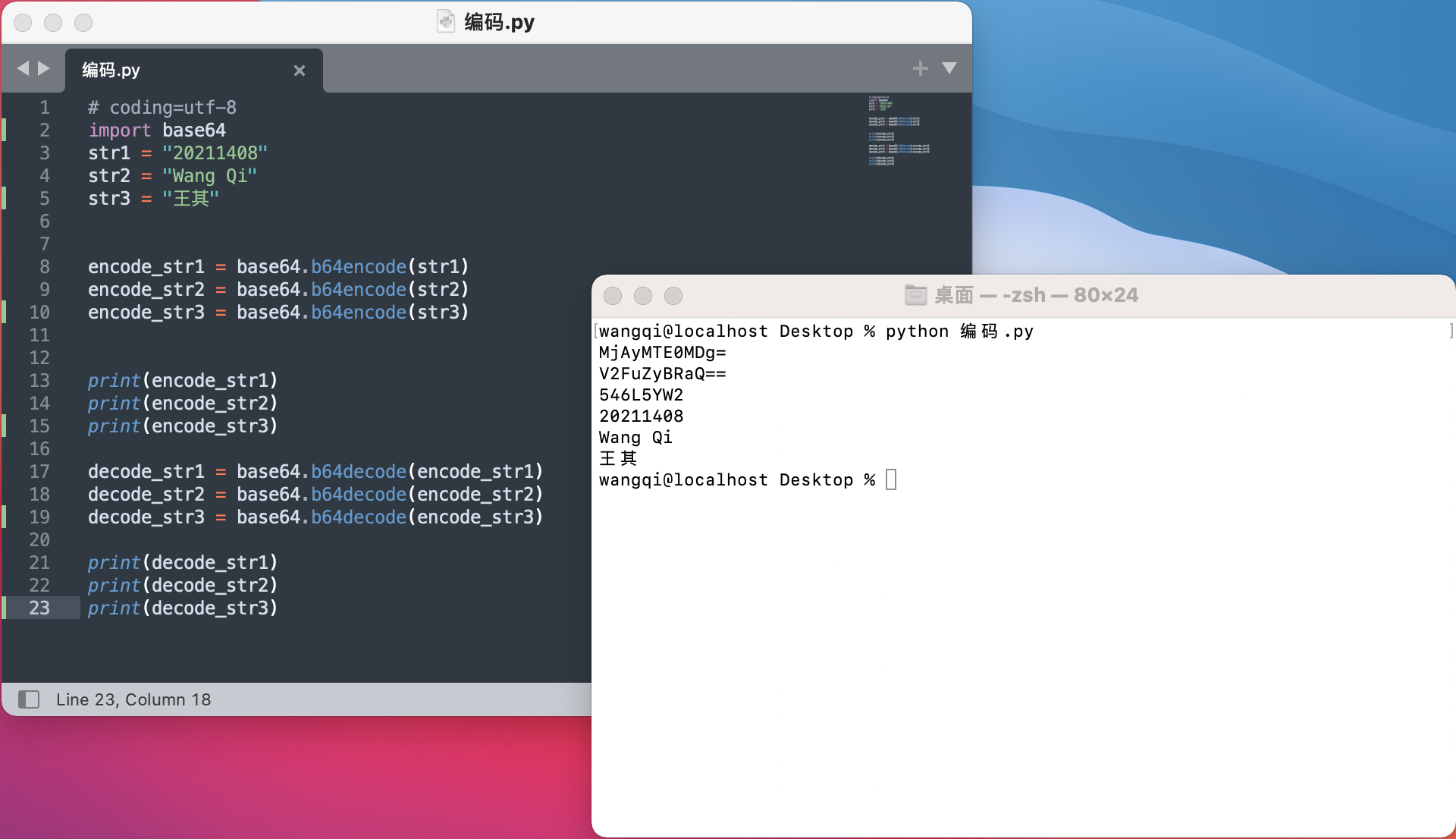
BASE64编码

IEEE754 浮点数

学习了如何将十进制的数转换为单精度浮点数，计算了三道题，在借鉴网络搜索到的代码的前提下添加了自己的内容。

也明白了编码和加密的区别，编码绝不是加密。编码和加密的区别，在于编码是通常希望别人解码的。而加密是不希望的。编码更多的是为了转换格式，加密是为了安全。解码，是编码的逆过程。解密，是加密的逆过程。
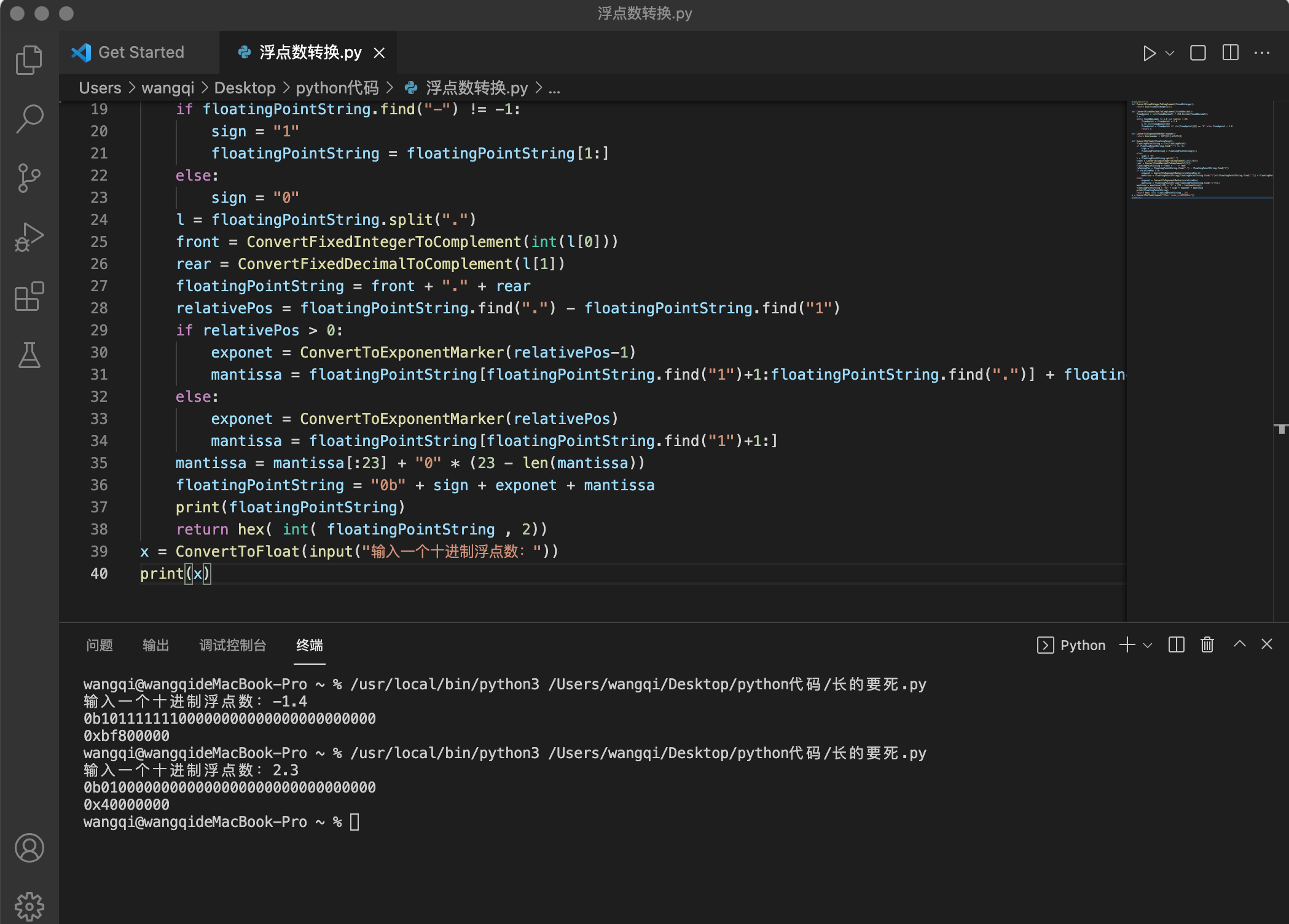
IEEE754 浮点数

罗马数字转阿拉伯数字

第一个任务很容易，第二个一开始我有点纳闷，因为老师给的链接罗马数字转换阿拉伯数字0~3999里数字的范围是从0～3999，可我的学号是八位数，远远超过这个范围，这个该如何转换？通过和同学的交流，想了一个办法，就是分段来，既然范围是0～3999，最大也不过是四位数，那么就把八位切成四位来完成。
罗马数字转阿拉伯数字

其中：我对代码原理尝试进行了理解，首先定义了函数，函数名称随意，意图在于通过函数实现罗马数字向阿拉伯数字的转换，接着定义了字典，根据罗马数字与阿拉伯数字的对应关系进行梳理，然后如果str是0这个字符，那么回到初始值即0；否则的话初始值定为0，进入for循环，当变量i从索引0到索引“str字符长度”的时候，如果i满足等于0或者i变量对应的函数值与i-1的函数值比大小，如果大于，则res叠加一个i的函数，否则i函数-2个i-1的函数，最后return所得res值，返回到输出值。接着就是人机互动的环节：输入罗马数字，根据输入进行上述操作，以阿拉伯数字输出。

教材学习中的问题和解决过程

• 问题1：对于加法器、半加器还有全加器的具体原理我一开始没有看的太明白
• 问题1解决方案：通过反复阅读，并通过上网查询，将几个逻辑框图都走了几遍，对加法的执行有了深入的了解，明白了半加器只能算两个数位的和，多个数位的二进制需要用到全加器，而全加器是在半加器基础之上
• 问题2：对于S-R锁存器，一开始我也没看的太明白，逻辑框图也没有走明白
• 问题2解决方案：反复阅读，反复理解，反复走图。最终明白了S和R是1的情况下可以进行保存数据，将S和R中任意一个暂时设置为0，X会根据运算逻辑变成你想存储的数据，也就是1或0，变成了以后迅速恢复S或R至1，也就完成了存储数据的操作，而那些大的数据就需要在此基础之上扩展这样的电路
• 问题3: 我的学号是八位，如何将范围0～3999的十进制转换为罗马数字
• 问题3解决方案：通过和同学的交流，想了一个办法，就是分段来，既然范围是0～3999，最大也不过是四位数，那么就把八位切成四位来完成。

代码调试中的问题和解决过程

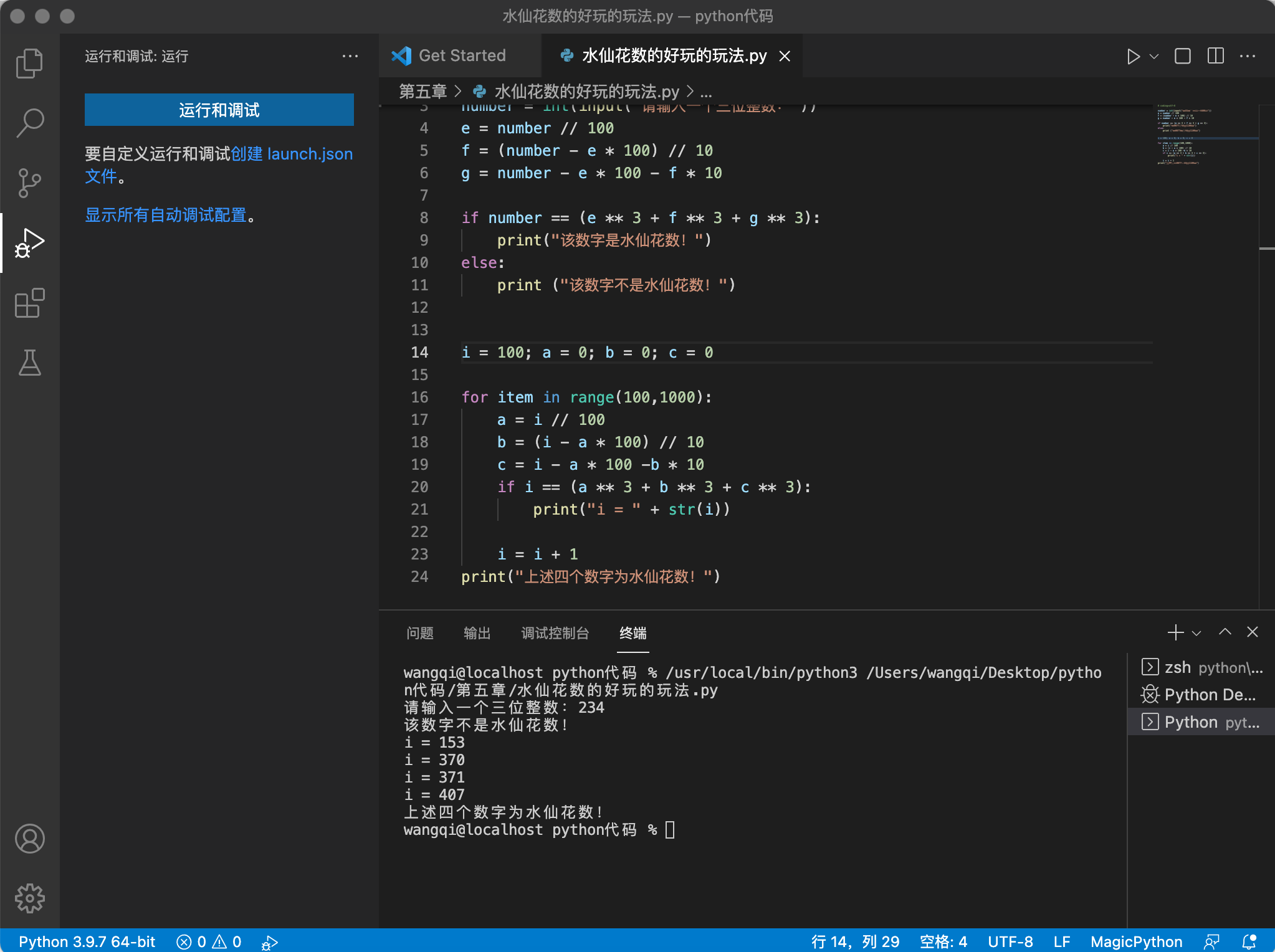
• 问题1：用for循环设计水仙花数的时候，将print（"上述四个数字为水仙花数")打在了for循环里，导致了程序运行的时候，循环之行了几次，那些字就被打印了几次，没有达到我预期的效果
• 问题1解决方案：将该代码移出for循环语句里
• 问题2：用base的时候没有运行成功
• 问题2解决方案：发现自己没有调用base64模块，补上去以后成功了。
• 问题3:在python运行IEEE754 浮点数转换的时候出现了很多不知所措的情况，比如面对原理毫无头绪等
• 问题3解决方案：网上搜索，对照着代码一点一点打到code上，然后试着运行了一下，目前用到的命令、函数等我还不知道，尝试根据注释去理解了编码原理，并上传至码云托管。其中我对最后一行的代码进行了修改，添加了人机互动，使得运行的时候先输入一个浮点数，再进行换算的步骤。

[代码托管]

托管
罗马数字转阿拉伯数字
罗马数字转阿拉伯数字（另）

上周考试错题总结

暂无

其他（感悟、思考等，可选）

感觉随着学习的深入，越来越觉得神奇

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	200/200	2/2	20/20
第二周	300/500	2/4	18/38
第三周	500/1000	3/5	22/60
第四周	300/1300	4/9	30/90

• 计划学习时间:30小时

• 实际学习时间:31小时

• 改进情况：阅读教材的时候思考时间有增加；针对代码的理解有进一步深入。

参考资料

• 《计算机科学概论》
• ...