java-排序
一,内部排序

有交换过程的都不稳定,
选择--待排序区选一个最值的出来-交换(不稳定)--不受初始序列顺序影响
①简单选择,②堆排序
交换--不停交换,使最值浮现。(不稳定)
③冒泡,④快排
插入--取一个待排序,在已排序序列不停比较,找到位置插入
⑥直接插入(稳定),⑦折半插入(稳定),⑧希尔排序(不稳定)
归并
⑨二路归并,两路插入,(稳定)
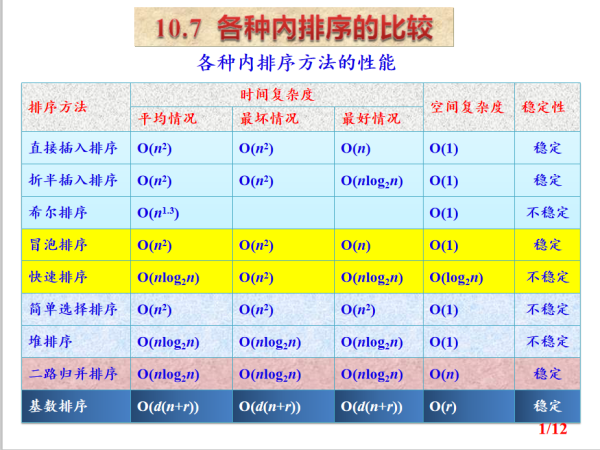
O(n^2):简单选择,插入(直接/折半),冒泡
O(n^1.3):希尔排序
O(nlogn):快排,堆排,二路归并
代码:

/** * 内部排序 * * 有交换过程的都不稳定, * * 选择--待排序区选一个最值的出来-交换(不稳定) * ①简单选择,②堆排序 * 交换--不停交换,使最值浮现。(不稳定) * ③冒泡,④快排 * 插入--取一个待排序,在已排序序列不停比较,找到位置插入 * ⑥直接插入(稳定),⑦折半插入(稳定),⑧希尔排序(不稳定) * ⑨归并 * 二路归并,两路插入,(稳定) * *⑩基数排序 (稳定) */ //升序 public class InnerSort { /** * 简单选择,无论有没有序,都要比较n(n-1)/2次,交换次数不确定。最少0次,最多3(n-1)次 *最好,最坏,平均时间复杂度都为O(n^2) */ public int[] easyChoose(int[] a){ for(int i=0;i<a.length;i++){ int index=i; for(int j=i+1;j<a.length;j++){ if(a[j]<a[index]){ a[index]=a[j]; index=j; } } if(index!=i) swap(i,index,a); } return a; } /** * 堆排序--小顶堆,每次堆顶与堆尾交换(不稳定),从新调整堆使顶最小。 *完全二叉树,-跟节点小于子节点a[i]<a[2i].a[i]<a[2i+1] * ①建堆 * ②筛选 * ③调整 * 建堆/调整堆--每次找子树的最小节点调到堆顶 * 新建/调整堆时,low=hign/2 * 堆排序数组[0]不能用,不满足双亲,2i,2i+1; * * */ private void sift(int[] a,int low,int high){ int i=low,j=2*i; int top=a[i]; while(j<=high){ //拿到i的两个孩子(2i和2i+1)中的较小的 if(j<high&&a[j]>a[j+1]) j++; if(a[i]>a[j]){//继续往子树遍历,直到找到子树中最小的小标i a[i]=a[j]; i=j; j=2*i; } else break; } a[i]=top; } public int[] heapSort(int[] array,int n){ int i,top; //初始堆 for(i=n/2;i>=1;i--){ sift(array,i,n); } //建完堆顶已经最小,直接交换,再排n-1次 for(i=n;i>=2;i--){ top=array[1]; array[1]=array[i]; array[i]=top; sift(array,1,i-1); } return array; } /** * 冒泡排序-改进版本,若已成序(无交换直接返回) * 最好O(n),最坏和平均:O(n^2) */ public int[] bubbleSort(int[] a){ int i,j; boolean exchange; for(i=0;i<a.length;i++){ exchange=false; for(j=a.length-1;j>i;j--){ if(a[j-1]>a[j]){ swap(j-1,j,a); exchange=true; } } if(!exchange)return a; } return a; } /** * 快排,选一个基准值,将小于基准值的放左边,大于基准值的放右边,在对左边和右边快排 * * 时间复杂度平均和最好O(nlogn),最坏O(n^2); * */ public int[] quickSort(int[] a,int low,int high){ int i=low,j=high,num = -1; if(low<high){ num=a[low]; while(i<j){ while(j>i&&a[j]>=num)j--; while (i<j&&a[i]<=num)i++; swap(i,j,a); } swap(i,low,a); quickSort(a,low,i-1); quickSort(a,i+1,high); } return a; } //直接插入排序,最好O(n),最坏O(n^2),平均O(n^2) public int[] easyInseart(int[] a){ for (int i=1;i<a.length;i++){ if(a[i]<a[i-1]){ int j=i-1; int num=a[i]; while(j>=0&&a[j]>num){ a[j+1]=a[j]; j--; } a[j+1]=num; } } return a; } //折半插-二分查找// --查找效率提高,总体交换次数没变,平均时间复杂度O(n^2) public int[] binInseart(int[] a){ for (int i=1;i<a.length;i++){ if(a[i]<a[i-1]){ int low=0,high=i-1; int num=a[i]; while(low<=high){ int mid=(low+high)/2; if(a[mid]<num) low=mid+1; else high=mid-1; } for(int j=i-1;j>=high+1;j--) a[j+1]=a[j]; a[high+1]=num; } } return a; } /** * 希尔排序 * d=n/2 * 将排序序列分为d个组,在各组内进行直接插入排序 * d=d/2,重复第二步,直到d=1;最后一步就是对所有数据进行直接插入排序 * * 平均时间复杂度O(n^1.3) */ public int[] shellSort(int[] a){ int i,j,d,num; d=a.length/2; while(d>0){ for(i=d;i<a.length;i++){ num=a[i]; j=i-d; while(j>=0&&num<a[j]){ a[j+d]=a[j]; j=j-d; } a[j+d]=num; } d=d/2; } return a; } //归并排序---O(nlogn) private void merge(int[] a,int low,int mid,int high){ int[] b = new int[high-low+1]; int i=low,j=mid+1,k=0; while(i<=mid&&j<=high) { if (a[i] <= a[j]) b[k++] = a[i++]; else b[k++] = a[j++]; } while(i<=mid) b[k++]=a[i++]; while(j<=high) b[k++]=a[j++]; for(k=0,i=low;i<=high;k++,i++) a[i]=b[k]; } public int[] mergeSort(int[] a,int low,int high){ if(low<high){ int mid=(low+high)/2; mergeSort(a,low,mid); mergeSort(a,mid+1,high); merge(a,low,mid,high); } return a; } /** * 基数排序 * 不用比较关键字大小, */ //交换函数 private void swap(int a,int b,int[] c){ int num=c[a]; c[a]=c[b]; c[b]=num; } //输出数组 private void printArray(int[] a){ System.out.print("数组:"); for(int i=0;i<a.length;i++){ System.out.print(a[i]+" "); } System.out.println(); } public static void main(String args[]) { InnerSort sort=new InnerSort(); int[] array={8,4,6,9,22,5,2,16,7,38,26}; sort.printArray(array); //array=sort.easyChoose(array); // array=sort.bubbleSort(array); // array=sort.quickSort(array,0,array.length-1); // array=sort.easyInseart(array); // array=sort.binInseart(array); // array=sort.shellSort(array); array=sort.mergeSort(array,0,array.length-1); sort.printArray(array); // int[] array1={0,8,4,6,9,22,5}; // sort.printArray(array1); // array1=sort.heapSort(array1,array.length); // sort.printArray(array1); } }
二,外部排序

①生成初始归并段:
1.1,普通方法,按内存大小,将文件分成若干子文件,长度基本相等,个数=N/w (记录数/工作区容量)
1.2,置换-选择算法,可以减少初始归并段数量,但各归并段长度较大,

②多路归并 败者树,--减少关键字比较次数
最佳多路归并:最短K叉哈夫曼树




 浙公网安备 33010602011771号
浙公网安备 33010602011771号