环形链表 II (Linked List Cycle II) 解题思路

原题目在https://leetcode-cn.com/problems/linked-list-cycle-ii/description/，这里粘一张图片：

 

这里为了满足不用额外空间的要求，一般采用链表操作的双指针技巧，也就是使用快慢指针的方式进行解题。

参考了很多博客和网页，大致有以下两种思路：

　　

　　1、快慢指针相遇时，让其中一个指针先走一圈数出环的节点个数，再让头指针先走环长度的步数，一个临时指针从原来头指针位置开始走，

             这样头指针比这个临时指针先走一个环的步数，它们每个阶段分别只走一步，相遇时侯自然是环的入口点

　　

　　2、快慢指针相遇时，让其中一个指针与头指针一起一步一步地走，相遇时侯就是环的入口点。

 

第一个思路清晰明了，第二个思路很巧，所以想证明第二个思路。严谨的数学证明想半天没出来，所以就画图说明吧：

如图，不妨先考虑环比较大的情况下，

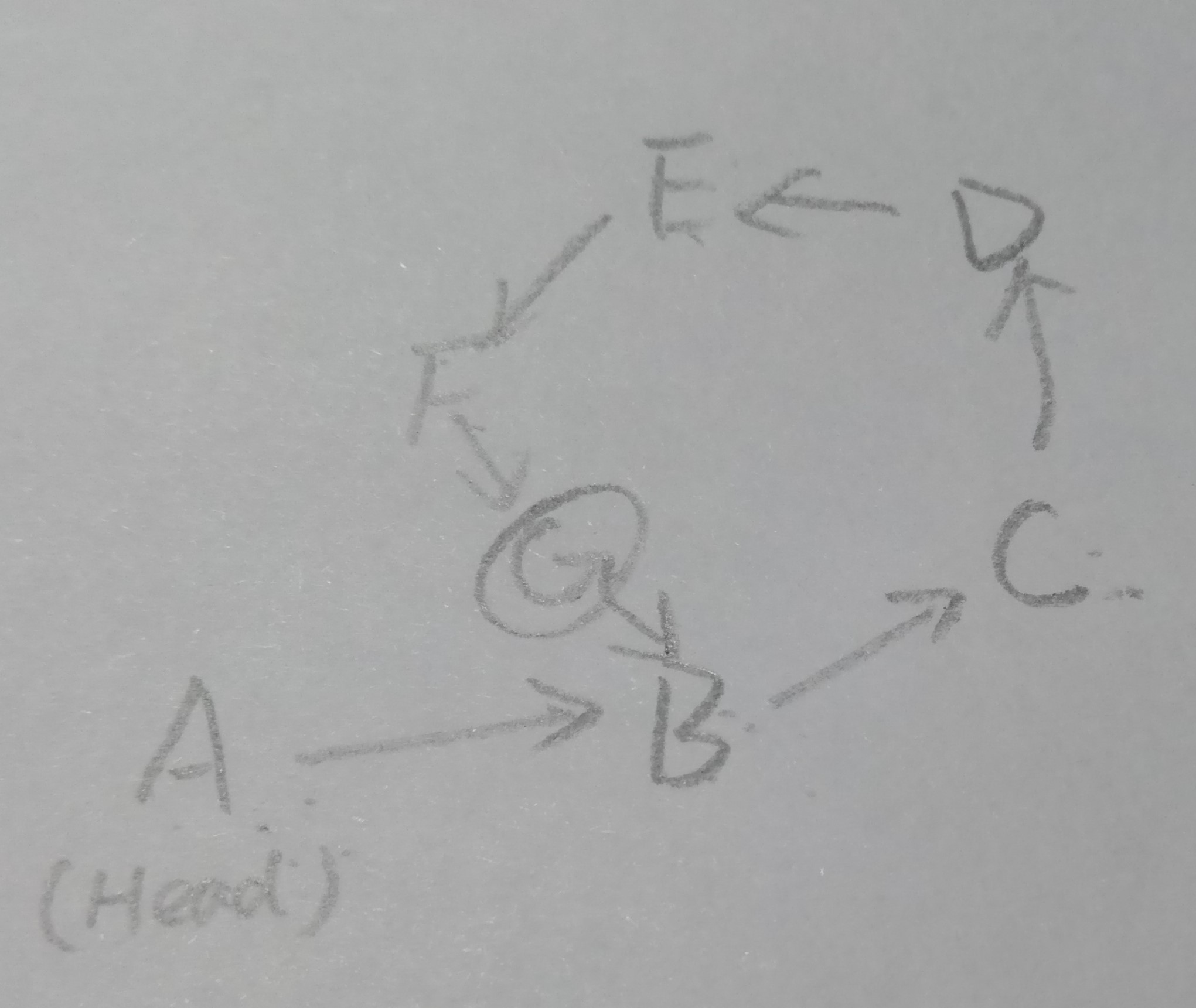
快慢指针在G处相遇，则可以认为快指针第二次到达G（环比较大，只绕了一圈），而慢指针第一次达到G点。

或者我们认为在慢指针达到G时快指针到达G后又整整绕了一圈（快指针速度是慢指针的两倍），也就是说慢指针走过的距离正好是环的长度的一倍（即相等）。

若将慢指针走过的节点重新组织成类似环的样子，如图所示：

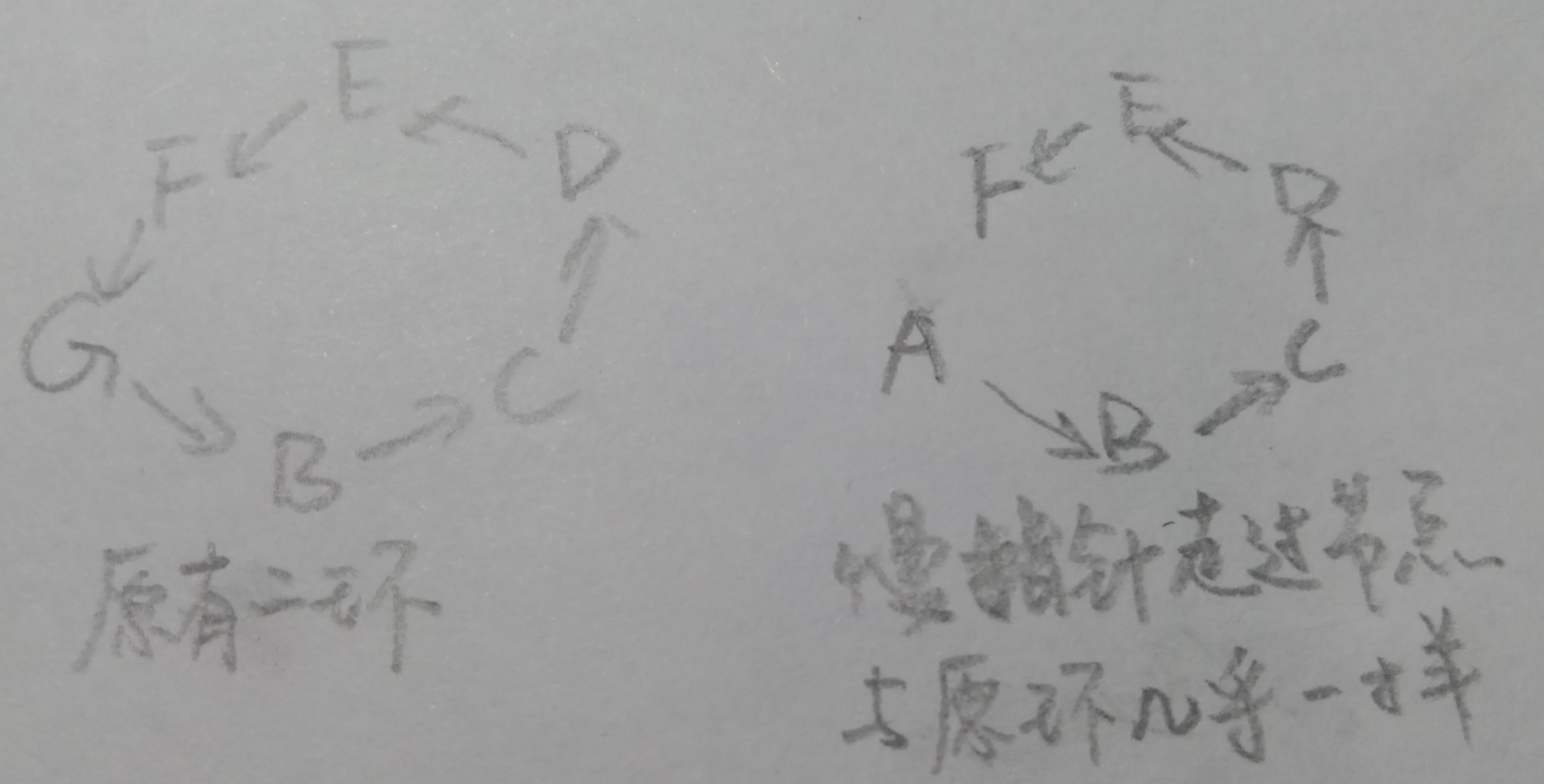
不严谨的说，除了末尾外这两个图是同构的。那么当两个节点分别从G和A出发时就会在第一个 两环同一位置都相同的节点 B处（入口处）相遇。

 

另外一个是考虑环比较小的情况，

此时快指针饶了很多圈到达G点与慢指针会合，不难想到有慢指针走过的距离是环的长度的n倍（也就是说慢指针走过的距离整除于环的长度），

仿照上面的证明方式，就不难得出结论了，无非一个是小环，一个是大环。或者你可以想象一个小环在大环中（大环不动）顺时针滚动的样子（方式GA-EB-FC-GD-EE-FF）

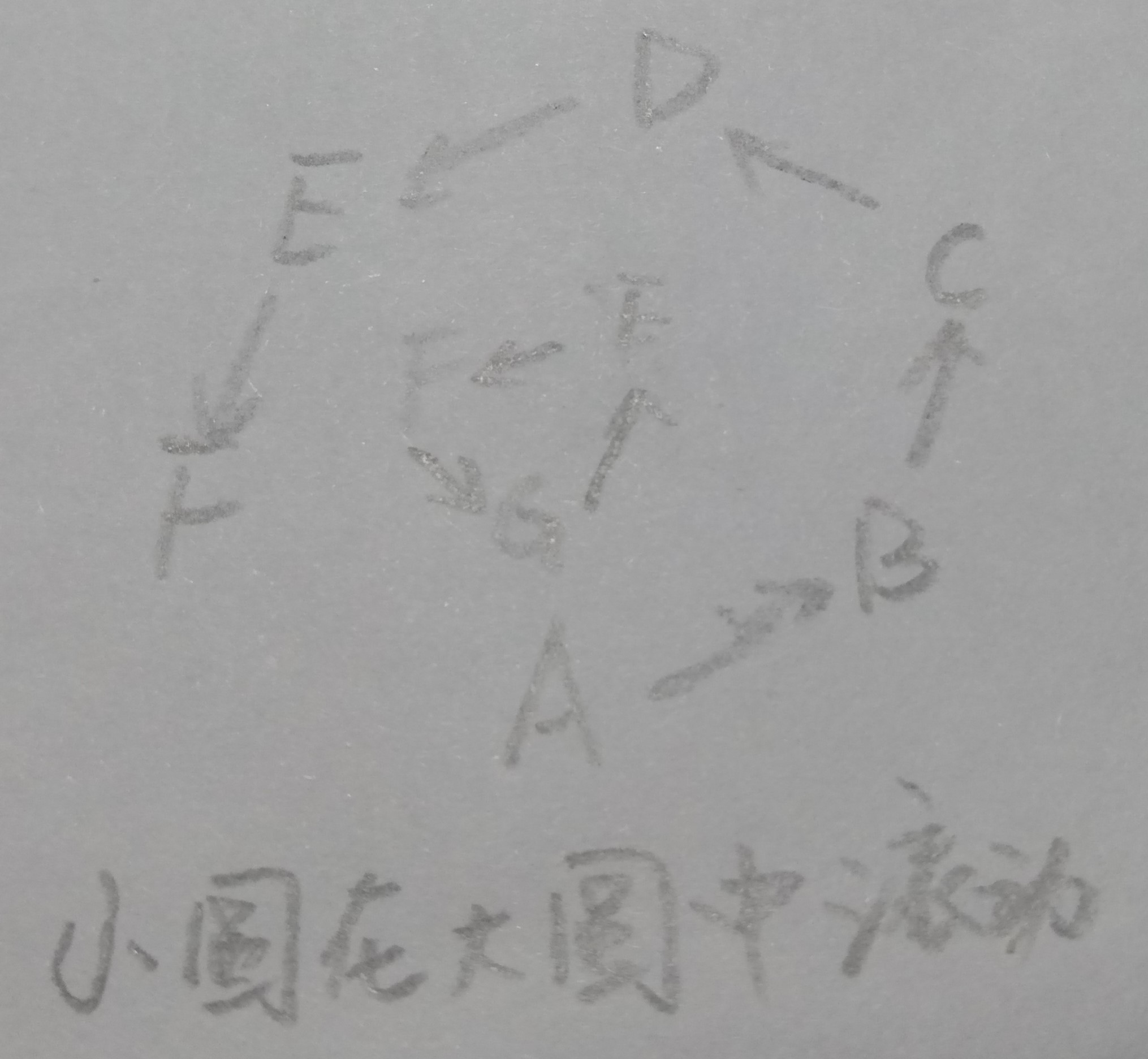
 滚动时第一个相同节点E就是入口处

下面贴出代码，注释部分是第一个思路需要的代码。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head==null || head.next==null)return null;
        ListNode q = head;
        ListNode s = head;
        while(q!=null && q.next != null){
            q = q.next;
            q = q.next;
            s = s.next;
            if (q==s)break;
        }
        if(q==null || q.next==null)return null;
//        int step = 1;
//        q = q.next;
//        while(q!=s){
//            step++;
//            q = q.next;
//        }
//        q = head;
//        while(step-->0)head=head.next;
        while(q!=head){
            q=q.next;
            head=head.next;
        }
        return q;
    }
}