x264 MB-tree实现细节
x264 MB-tree实现细节
MB-tree的直白定义:帧和帧之间有引用关系,那些被引用的帧应该有更高的精度。通过这样的调整,只需调整一帧的精度,就能有效改善一连串画面的质量。
所以接下来要解决两个问题:
- 怎么判断帧和帧之间的引用关系,这里称呼为propagate(遗传)关系。
- 一个往往被忽略,但其实比第1个问题更重要的事情:MB-tree工作的上下文。(MB-tree什么时候发生的,在哪发生,以及它本身对上下文的要求。)
首先聊一聊MB-tree的上下文
MB-tree的设计是放在lookahead阶段的,参考的数据并非原始帧,而是经过向下采样之后的lowres数据,它所在处理阶段如下:
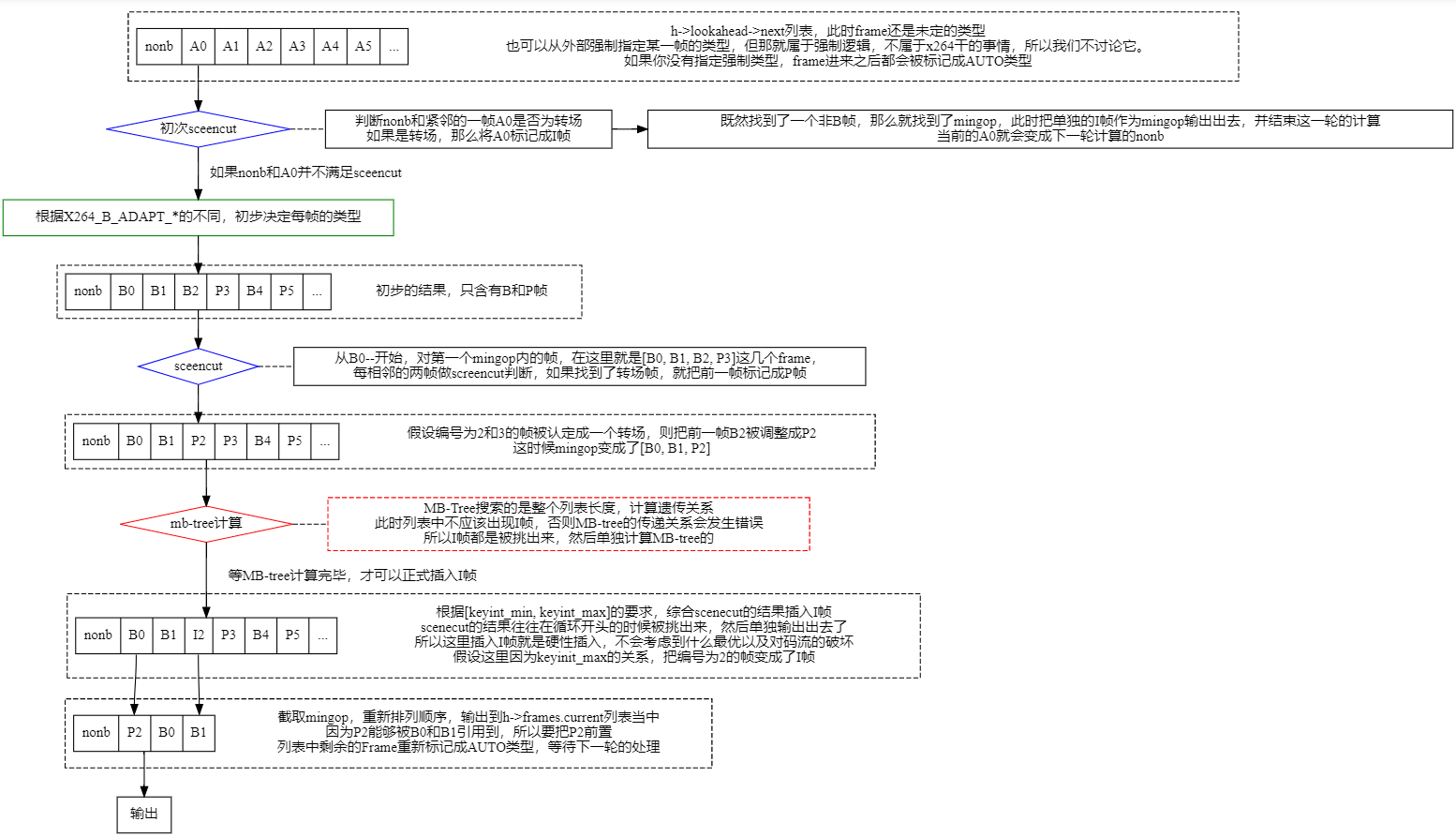
在lookahead阶段,一个帧序列被初步设定之后,它们之间的引用关系就是固定的,MB-tree所在的阶段只有P和B帧,它们之间的关系也是一种固定关系:
-
P只会引用紧邻的前一个P帧
-
B帧只会引用紧邻的两个非P帧
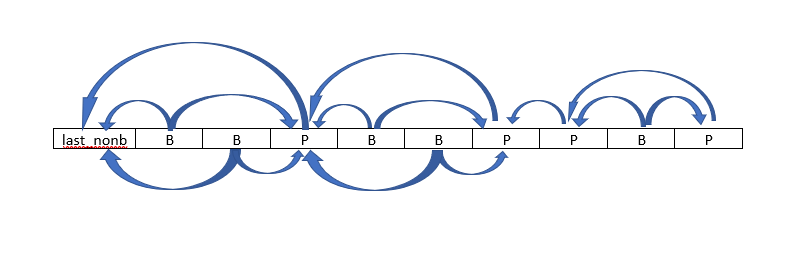
为什么这里不能有I帧?:
因为这里是lookahead阶段,为了简化计算,所以才把引用关系弄成了一种固定结构。但正式编码阶段,引用关系并非如此,B可以横跨数个P帧直到找到最优的引用,P帧也是如此。
如果在lookahead阶段就插入I帧,那么I帧因为不会引用别的帧,就会导致MB-tree的遗传链发生断裂。但在正式编码阶段,因为可以横跨数个引用帧,即便有I帧遗传关系也不会发生断裂。
故而在这里,x264的做法是先不要把I帧标记出来,让I帧先伪装成B或者P,等MB-tree计算完毕之后,再把I帧标记出来。
确定了引用关系,模型就定下来了,接下来才可以正式的计算遗传关系。
帧之间的继承、遗传关系:
对于所有帧来说,互相引用的关系都可以用如下模型表示:(P帧是b==p1的特殊情况)
在计算MB-tree模型的时候,是按照一对一对的来算,比如上面的b帧同时引用了p1和p0,那么就先计算P0传递给b多少信息,再计算p1传递给b多少信息。
首先,要调用slicetype_frame_cost,计算出b同时引用p0,p1得到的MB级别的inter_cost和intra_cost。inter_cost越小,就代表b从外部继承的信息越多。
因为数据是MB级别的,所以在x264中看到的数据结构是一串一串的列表,分别记录每个MB的数据。而我们将要谈到的计算模型,也都是以一个个MB为单位,对一帧内的所有MB都要计算一遍,最后得到MB级别的控制。
如何计算MB-tree的propagate信息
MB-tree采用的是简单的线性模型(b和p0的遗传关系):
显然这个模型是有一点问题的:
-
既然b同时从P0和P1都继承了信息,那么是不是该有一个比例问题?
没错,需要一个ratio来修正上面的公式,按照距离来设置:b到p0的 distance_ratio= (b - p0) / (p1-p0)
-
之前我们讨论了AQ的策略,AQ在不改变码流的情况下,将各个MB都进行了微调,那么那些被调整的更清晰的MB(QP减小)和变得更模糊的MB(QP变大),在这里是不是也该考虑一下影响?
也完全正确!变得模糊的MB携带的信息更少,理应再加一个修正因素。量化的过程就是把系数除以QStep,所以这里的修正因子也很简单:inv_qscale = 1.0/aq_offset_step
-
在VFR视屏下,也就是可变帧率Frame,这时候每一帧占据的播放时间都不一样,有些帧可能在屏幕上停顿更长的时间,是否代表这些帧更重要?
|完全正确!让我们再加一个修正因子:fps_factor = b帧停留的时间/平均一帧停留的时间
让我们先解决以上三个问题,修正公式如下:
但还差一些:
让我们再回顾一下MB-tree的目的,它想通过遗传计算,找出那些被引用的帧,然后给这些被引用帧增加码流(通过降低QP来增加码流),而引用本身就是一种传递机制。
假设:A引用了B,然后B又引用了C,在这种情况下C和B都被人引用了,但C的重要性显然比B更高,因为C才是一切的源头。如果C的清晰度不够,那么C会把它恶劣的画面传导给B,然后B又传导给了A。
故而MB-tree的遗传信息,应该是一层一层往上传递的。
让我们再做最后的一点修正,让数据累加起来,一层层的往上游传递,给每个Frame都增加一个propagate变量来记录它遗传了多少信息给别的帧(b遗传了propagate_b的信息给别的帧),然后在计算p0遗传信息的时候,自然要加上propagate_b:
propagate_b不应该乘以fps_factor,所以做了一些小的调整。
最后这个公式算出来的,就是p0所携带的propagate(遗传)信息,当然不止b这一帧会引用p0,其余的帧也会引用到p0,所以p0最后的propagate信息应该是所有信息之和。
在lookahead阶段,所有帧之间的引用是一种简单的固定关系,我们只要按照编码的反顺序依次遍历所有帧,就可以算出所有帧的遗传信息。
其中,B帧并不会引用别的帧,故而B帧是没有遗传信息的,但是要注意BREF是包含遗传信息的。
遍历所有MB,以MB为最小单元进行计算:
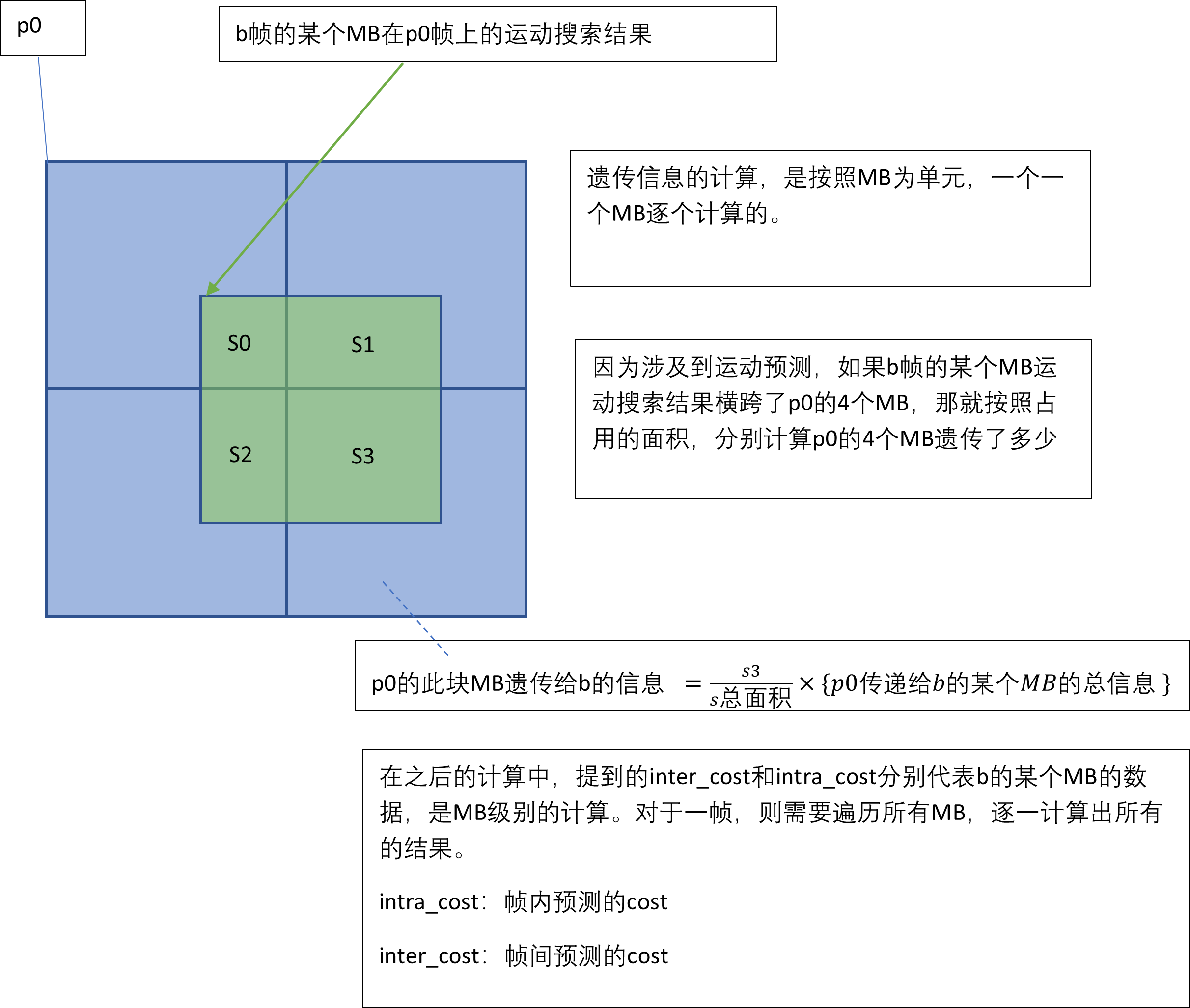
得到了P0的propagate,是时候调整P0的清晰度了
MB-tree采用的公式依旧很简单,是个线性转化过程,先让我们看一个大体的框架公式(后面还要一点点的修正它):
首先要明白一件事,在计算MB-tree的调整结果的时候,是以MB为单位的,每个MB有两个重要的参数propagate(遗传给后续帧的信息)和MB的intra_cost(MB自身包含的信息)。
故而,首先我们想到的MB-tree QP的方案如下(算出来的比例,需要通过log2函数转化成QP):
这里要考虑的第一个因素是intra_cost虽然是p0的自身信息,但没有考虑到p0在屏幕上停留的时间,p0停留的时间越长,代表intra_cost的比重应该越大,故而需要进行修正因素fps_factor = (p0在屏幕上停留的时间 ) / (平均一帧在屏幕上停留的时间),然后修正如下:
如此一来,这个公式就基本成型了,唯一麻烦的是x264在设计的时候,给使用者提供了外部的参数h->param.rc.f_qcompress:
f_qcompress被定义出来,就是为了动态调整QP变化的强度,所以MB-tree在利用QP调整精度的时候,也要参考这个变量。
在考虑到f_qcompress的影响之后,修正如下:
将固定系数设定成5(我也不知道为什么是5,为什么不是4,不是3……)
最后变成:
理论上这里已经很完善,考虑了各种因素,只是x264的lookahead设计上欠缺了一些:
PSY优化(此前的代码解释可能有误,经过仔细思索后修改如下):
之前一直认为这里是Weight-P的修正,但仔细揣摩了一遍代码,发现x264在计算frame cost的时候已经考虑到了Weight-P的影响。
在开启PSY的时候,lookahead阶段会对Weight-P的结果,根据i_subpel_refine的等级进一步优化,找出更合理的Weight-P的系数。所以如果开启了Weight-P,那么这个更合理更优秀的结果,本该可以作用于PSY特性。可如果你没有开启Weight-P这个功能,那么PSY是一定会损失精度的,所以PSY就报复似的在这里提高了MB-tree参考帧的精度,以求得更优秀的画面。
关于为什么要这么做,还没有思索清楚,只能给一个初步的猜测……如果有谁知道它背后的理论基础,也欢迎一起讨论下
所以猜测:如果你关闭了Weight-P,那么MB-tree就会提高参考帧的精度。提高的精度比例如下:
把上述修复因子带入正式的MB-tree结果。
考虑到PSY优化之后的结果:
MB-tree的整个流程就摆在这里了,计算完毕之后,要把MB-tree的结果存放在如下数据结构中:
f_qp_offset[mb_index] = f_qp_offset_aq[mb_index] - qp_offset;
//qp_offset: MB-tree的结果,因为qp越小代表的精度越高,所以这里是减去它
//f_qp_offset[mb_index] : 是保存MB-tree结果的地方,但是别忘了AQ的结果,这里要加上AQ的结果f_qp_offset_aq[mb_index]
所以最后f_qp_offset[mb_index]中保存的是MB-tree和AQ的综合结果。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号