算法与数据结构——树
树
树的定义
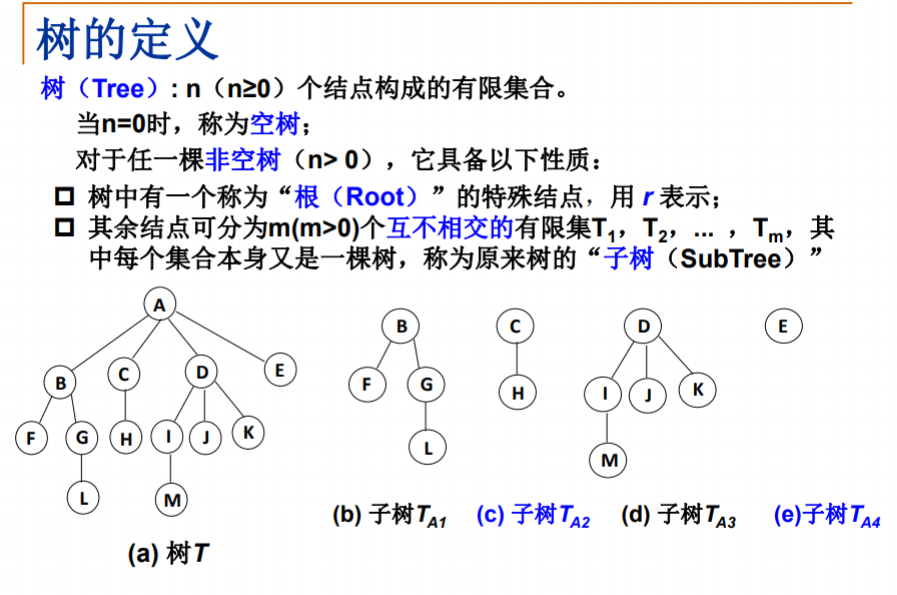
注意
-
子树是不相交的
-
除了根节点外,每个节点有且仅有一个父节点
-
一棵N个结点的树有N-1条边
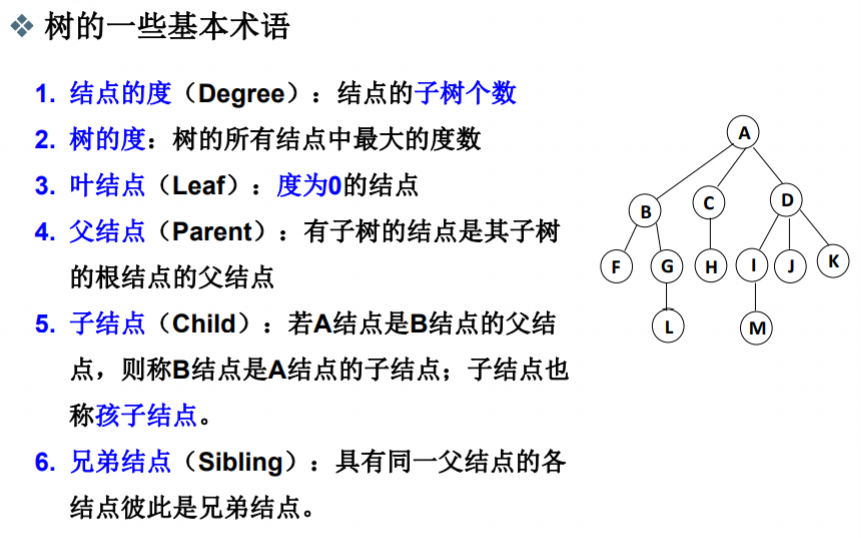
树的基本术语

树的实现
- 儿子兄弟表示法
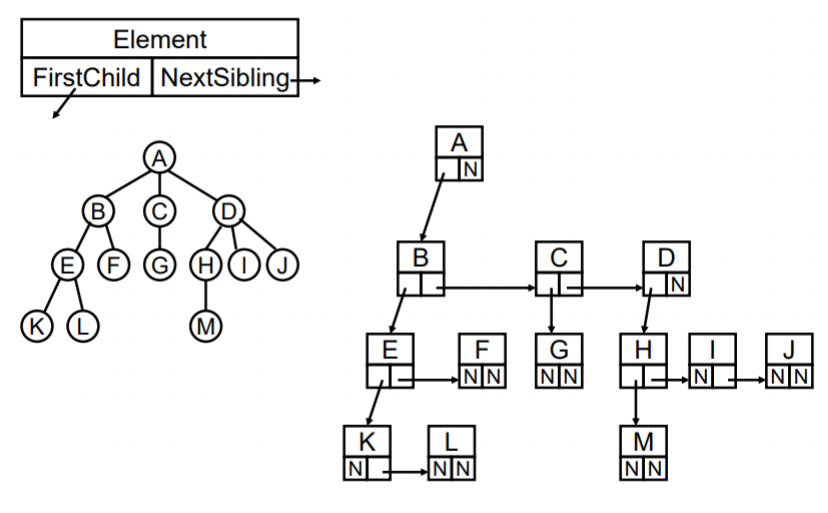
typedef struct TreeNode* PtrToNode;
//也可以理解为左儿子右兄弟表示法
struct TreeNode
{
ElementType Element;
PtrToNode FirstChild; //左儿子
PtrToNode NextSibling;//右兄弟
};
二叉树
-
二叉树的定义
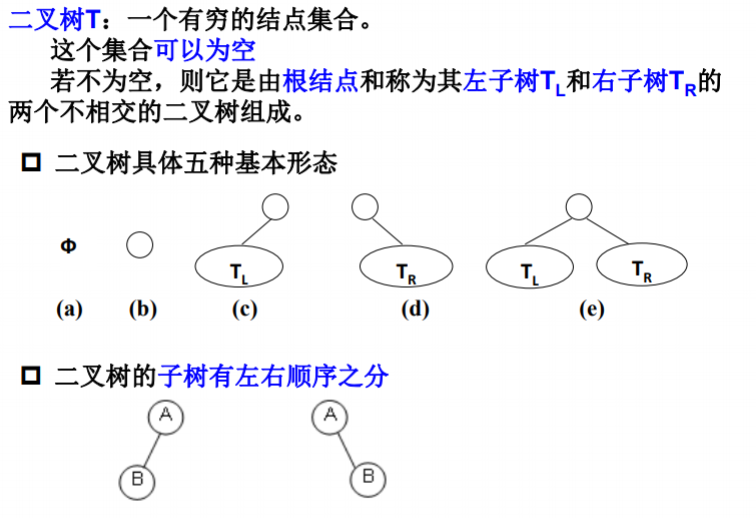
-
特殊二叉树
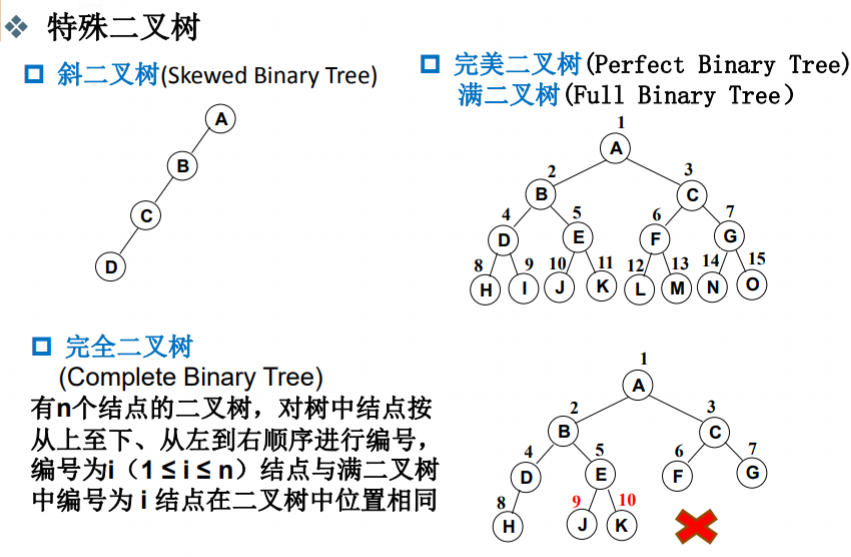
3.二叉树的几个性质
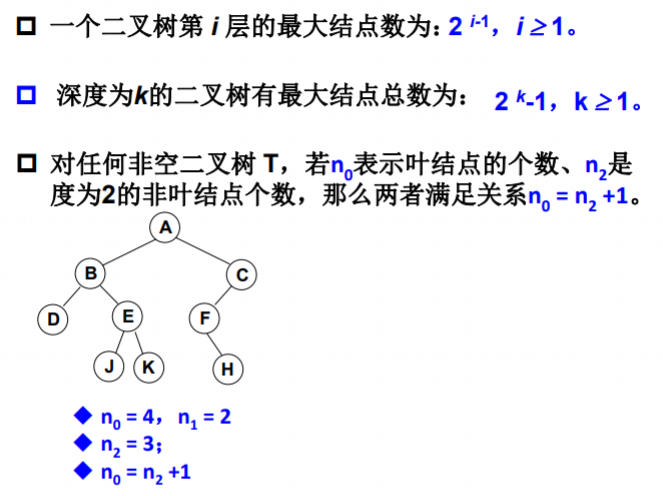
- 高度h≥0的二叉树至少有h+1个结点
- 含有n≥1个结点的二叉树的高度至多为n-1
- 二叉树的遍历
*先序遍历

*中序遍历
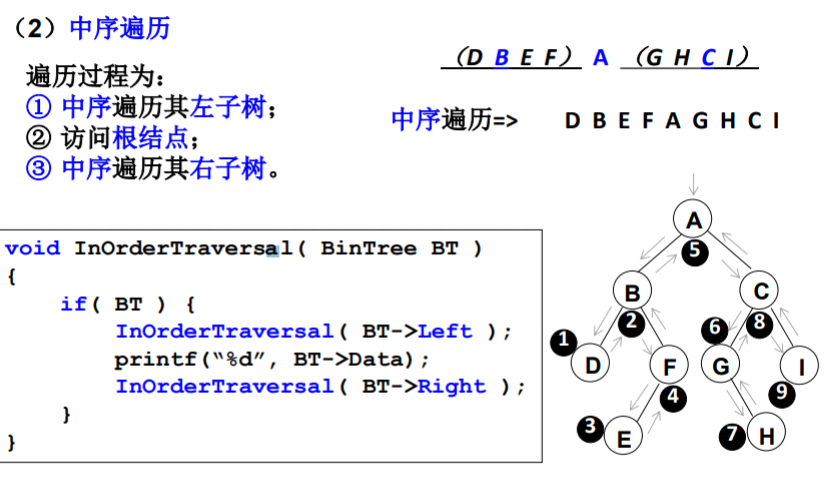
*后序遍历


- 先序、中序和后序遍历过程:遍历过程中经过结点的路线一
样,只是访问各结点的时机不同。
二叉树分类
完全二叉树,满二叉树,平衡二叉树,扩充二叉树等等
二叉树的应用
- 普通的二叉树,很难构成现实的应用场景,但因其简单,常用于学习研究,平衡二叉树则是实际应用比较多的。常见于快速匹配、搜索等方面。
- 常用的树有:AVL树、红黑树、B+树、Trie(字典)树。
1、AVL树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
2、红黑树: 平衡二叉树,广泛用在C++的STL中。如map和set都是用红黑树实现的。还有Linux文件管理。
3、B/B+树: 用在磁盘文件组织 数据索引和数据库索引。
4、Trie树(字典树): 用在统计和排序大量字符串,如自动机、M数据库索引。
二叉树实现
1.二叉搜索树
struct TreeNode
{
ElementType Element;
SearchTree left;
SearchTree right;
};
//建立一颗空树
SearchTree MakeEmpty(SearchTree T)
{
if (T != NULL)
{
MakeEmpty(T->left);
MakeEmpty(T->right);
free(T);
}
return NULL;
}
//查找操作
Position Find(ElementType X, SearchTree T)
{
if (T == NULL)
return NULL;
if (X < T->Element)
{
return Find(X, T->left);
}
else if (X > T->Element)
{
return Find(X, T->right);
}
else
{
return T;
}
}
//递归实现查找最小元素
Position FindMin(SearchTree T)
{
if (T == NULL)
{
return NULL;
}
else if (T->left == NULL)
{
return T;
}
else
{
return FindMin(T->left);
}
}
//非递归查找最大元素
Position FindMax(SearchTree T)
{
if (T != NULL)
{
while (T->right != NULL)
{
T = T->right;
}
}
return T;
}
//插入元素到二叉搜索树中
SearchTree Insert(ElementType X, SearchTree T)
{
if (T == NULL)
{
T = new TreeNode;
if (T == NULL)
{
cout << "out of space";
}
else
{
T->Element = X;
T->left = T->right = NULL;
}
}
else
{
if (X < T->Element)
{
T->left = Insert(X, T->left);
}
else if (X > T->Element)
{
T->right = Insert(X, T->right);
}
//Else X is in the tree already;we will do nothintg
return T;
}
}
//删除
SearchTree Delete(ElementType X, SearchTree T)
{
Position TmpCell;
if (T == NULL)
{
cout << "Element not found";
return;
}
else if (X < T->Element)
{
T->left = Delete(X, T->left);
}
else if (X > T->Element)
{
T->right = Delete(X, T->right);
}
//Find the element to delete
else if (T->left && T->right)
{
TmpCell = FindMin(T->right);
T->Element = TmpCell->Element;
T->right = Delete(T->Element, T->right);
}
else//handle Zero or One children
{
TmpCell = T;
if (T->left == NULL)
{
T = T->right;
}
else if (T->right == NULL)
{
T = T->left;
}
free(TmpCell);
}
}


