二维码的秘密
二维码的秘密
最近在做一个项目,需要做App扫码登录,前端利用websocket,监听后端扫码成功的响应来实现登录。我用了qrcodejs来生成二维码,二维码生成出来的时候,我有一些疑惑:
- 它的容量有多大?
- 二维码里面三个大方块是干什么的?
- 能存储视频/音频吗?
- 破损了为什么还能被识别?
- 生成原理是怎样的?
带着这些疑问,查阅相关资料,得到了我想要的答案
诞生和普及
上个世纪60年代,日本迎来高速增长期,卖食品、衣服等种类繁多的超市开始在城市中出现,当时超市使用的现金出纳机要靠手动输入商品价格,因此负责现金出纳的人常常会因手腕的麻木和“腱鞘炎”而苦恼。

技术是第一生产力,条形码的出现解决了这个问题,因此,条形码得以普及,条形码也叫一维码,缺点是,它的容量非常有限,最多能容纳20个英文字符和数字。怎么办?有个日本人,他叫原昌宏,投入了二维码的研发,一年半后,几经曲折,二维码诞生了。
二维码共有40个版本,每个版本有固定的码元数。码元是什么?就是位,1码元等于1bits。第一个版本(version 1)的码元数为21码元×21码元,version 2的码元数为25码元×25码元,每个版本横向和纵向各自以4码元为单位递增,以此类推
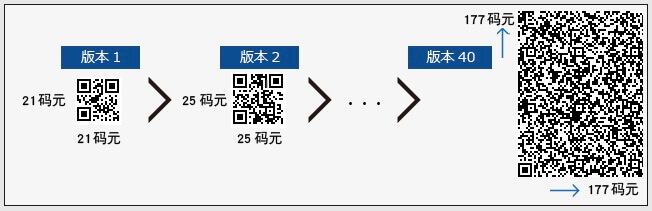
一维码和二维码
二维码翻译成英文为QR Code,全称为Quick Response Code,即快速响应码,二维码研发之初,有两个重点,一个是可以容纳大量信息,另一个就是可以快速读取。二维码跟一维码比起来,优点显而易见,以下是两者之间的差异
| 类型 | 差异 |
|---|---|
| 一维码 | 1、容量较小:30个字符左右 2、只能包含字母和数字 3、尺寸相对较大(空间利用率低) 4、遭到破坏后无法读取 |
| 二维码 | 1、数据容量大 2、超越了数字字母的限制 3、尺寸相对较小 4、被破坏依然可以被读取 |
二维码图形拆解
在继续深入了解二维码之前,先观察二维码图片,了解一些基本概念

二维码左上角、右上角以及左下角都有一个回形方块,右下方有一个小的回形方块,他们的作用是什么?剩下的都是一些类似于像素点的黑白方块,他们是怎么来的?
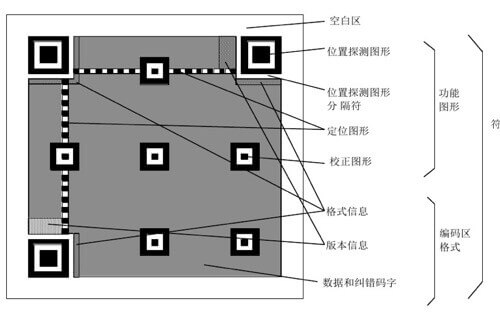
三个大方块,即位置探测图形,用来标记二维码的大小和方向
定位图形:二维码图形过大时,扫码容易畸形,定位图形就来防止畸形的产生
校正图形:版本2及以上才有
格式信息:包括纠错等级、掩码类别
版本信息:二维码的版本
数据和纠错码字:数据码和纠错码
出现了一些新概念,暂时不理解不要紧,往下看
二维码优点
1、存储大容量信息

一图胜千言,一个小小的二维码,可以存储成百上千个字符,具体容量跟二维码的版本有关,版本越大,容量越大
最小的版本1能存储41个数字 || 25个英文+数字 || 10个汉字
最大的版本40能存储7089个数字 || 4296个英文+数字 || 1817个汉字
2、在小空间内打印

相对而言,二维码占用的空间比一维码小得多
3、有效处理各种文字

二维码可以存储各种文字,因为最终都是转换成二进制
4、具备纠错能力
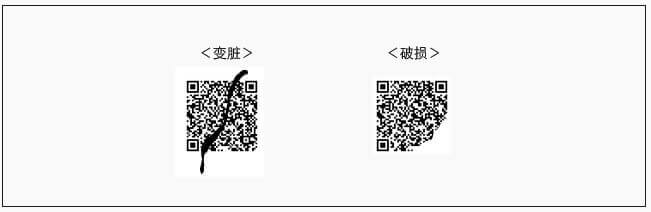
二维码小部分破损,仍然可以被读取,因为二维码有纠错能力,纠错能力还分为4个级别,分别是:
- L级,恢复率7%
- M级,恢复率15%
- Q级,恢复率25%
- H级,恢复率30%
级别越高,纠错能力越强,但由于数据量会随之增加,二维码尺寸也会变大。
纠错级别的恢复率,是指全部码字与可以纠错的码字的比例。例如,一共有100个码字(数据码),要对其中50个进行纠错,纠错级别为Q,则需要纠错码的个数等于50/0.25 - 100 = 100,也就是需要100个纠错码,加上数据码一共200个码字。
码字是什么概念?1个码字 = 8个码元,一个码元 = 1bits
5、360度方向读取
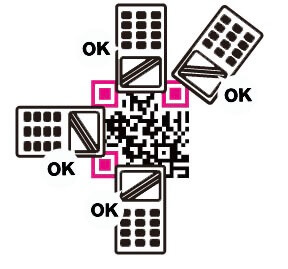
二维码可以从任何角度读取
6、支持数据合并
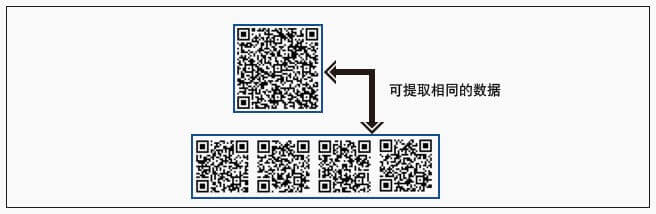
一个二维码可以拆分为多个,多个也可以合并为一个
安全性

2018年9月,出现了一些二维码,iPhone扫码后,立刻重启,这是因为二维码指向一个包含成千上万个div,设置了特定的样式,耗尽了iPhone的资源,而触发了iPhone的自我保护机制,重启了。这说明二维码带来便利的同时,也存在一些安全问题。
扫描二维码可以跳转到指定URL,是因为URL转换为二进制存储在二维码里面,因此所有基于URL的攻击,都有可能存在二维码中,什么网络钓鱼、传播恶意软件、SQL注入、XSS之类,甚至可能二维码本身就是恶意URL编码生成的,也可能是正常的二维码生成后被篡改,针对前者,要做的就是不去扫描来源不明的二维码,针对后者,解决方式无外乎两种:
第一种:非对称加密,二维码生产者用私钥加密,解码工具用生产者的公钥解密,类似于证书校验。
第二种:将二维码生成hash值,和URL一起编码到二维码内容里,解码工具将扫描到的二维码内容生成hash,与二维码内自带的hash比对一致,意味着二维码没有被篡改过。
二维码生成原理
生成原理,重点是数据码和纠错码的生成
数据码的生成
先上4个表
表1,模式编号指示器
| Mode | Indicator |
|---|---|
| 数字 | 0001 |
| 字母数字 | 0010 |
| 8位字节 | 0100 |
| 日文 | 1000 |
| 中文 | 1101 |
| …… | …… |
表2,字符计数指示器中的位数
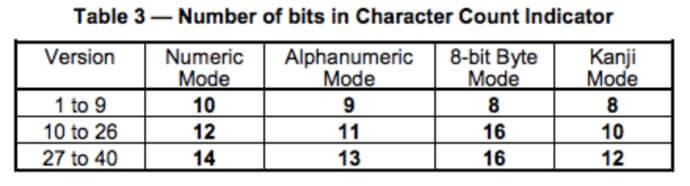
表3,字符映射表
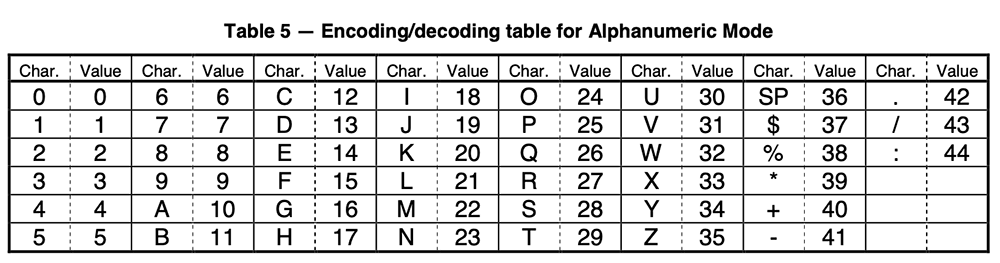
表4,二维码版本对应的码字数(第2列)和纠错码数(第4列)
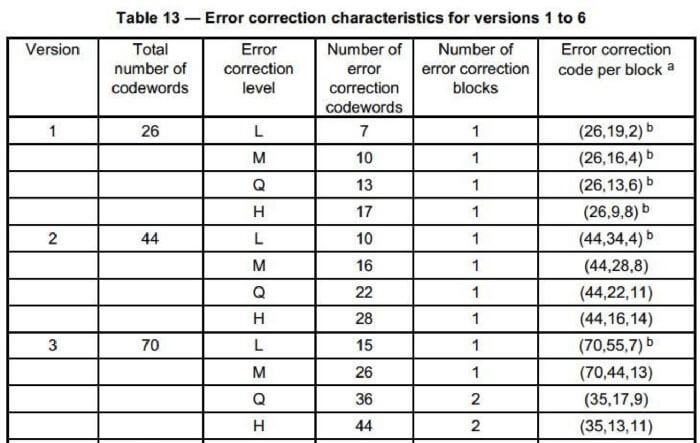
案例:将数字01234567编码,指定版本为1,纠错级别为Q
1、将数字3位为1组,分为3组:012,345,67
2、分别将3组数字转换成二进制,二进制长度为10(查表2,可知版本1-9,数字位数为10),012转成0000001100,345转成0101011001,67转成1000011,最后的67转换的长度为什么不是10位而是7位?分组后,不足3位的组,转换为4位或7位
3、把数字的个数转成二进制:01234567长度为8,8的二进制是0000001000,长度同样是10位
4、把数字编码的标志0001(查表1可得)和第3步的编码加到前面,得到如下编码
| 模式编号 | 字符数 | 数据编码 |
|---|---|---|
| 0001 | 0000001000 | 0000001100 0101011001 1000011 |
5、在末尾加上结束符,结束符固定为4个0,得到如下编码
| 模式编号 | 字符数 | 数据编码 | 结束符 |
|---|---|---|---|
| 0001 | 0000001000 | 0000001100 0101011001 1000011 | 0000 |
如果编码长度不是8的倍数,需要在后面继续补0,目前一共是83bits,需要补5个0,得到
| 模式编号 | 字符数 | 数据编码 | 结束符 | 不是8的倍数补0 |
|---|---|---|---|---|
| 0001 | 0000001000 | 0000001100 0101011001 1000011 | 0000 | 00000 |
6、未达到最大bits数限制(每个版本都有最大bits上限,查表4可得,版本1,纠错级别Q,总码字数26,纠错码占了13个码字,那么数据码为26 - 13 = 13个码字,最大bits数限制为13*8 = 104bits),末尾加补齐码,重复11101100 00010001直到达到最大限制,得到
| 模式编号 | 字符数 | 数据编码 | 结束符 | 不是8的倍数补0 | 补齐码 |
|---|---|---|---|---|---|
| 0001 | 0000001000 | 0000001100 0101011001 1000011 | 0000 | 00000 | 11101100 00010001 |
以上编码即为数字01234567的数据码,字符(英文+数字)的编码略有不同,相同的是编码都很繁琐
纠错码的生成
纠错码,使得有些二维码污损了也能扫码解析,主要是通过里德-所罗门纠错算法(Reed-Solomon Error Correction)实现的,这个算法,比较复杂,感兴趣的可以看看相关链接
二维码绘制
有了数据码和纠错码,就可以开始绘制二维码了,对照上文的二维码拆解图,绘制分为以下几步
1、 位置探测图形:不管二维码版本是多少,位置探测图形固定为7×7码元
2、 定位图形
3、 校正图形:不管二维码版本是多少,位置探测图形固定为5×5码元
4、 格式信息,包括纠错等级、掩码类别:格式信息固定为15bits,其中5bits数据位,10bits纠错位
- 5bits数据位中,2bits表示纠错等级,3bits表示掩码类别
纠错等级编码表
| 纠错等级 | 二进制编码 |
|---|---|
| L | 01 |
| M | 00 |
| Q | 11 |
| H | 10 |
掩码,是在填充完数据码和纠错码之后,和数据区(包括数据码和纠错码)进行异或运算,让二维码中黑色块和白色块分布得更均匀一些,便于解码
掩码类别共有8种,二进制编码分别是000、001、010、011、100、101、110、111,下面的图片印刷有误,最后两种编码写成一样,计算表达式也写成一样,实际最后一个编码为111,计算表达式为 ((ij)mod 3 + (i + j)mod 2) mod 2 = 0,很多文章都没有纠正这一点

5、版本信息:版本7及以上的二维码才需要加入版本信息
6、填充数据码和纠错码:数据码和纠错码都是一串长长的二进制数,每8bits为一块,即一个码字,填充顺序从右下角往上逐个填充,到顶后再从上往下填充,以此类推,如下图
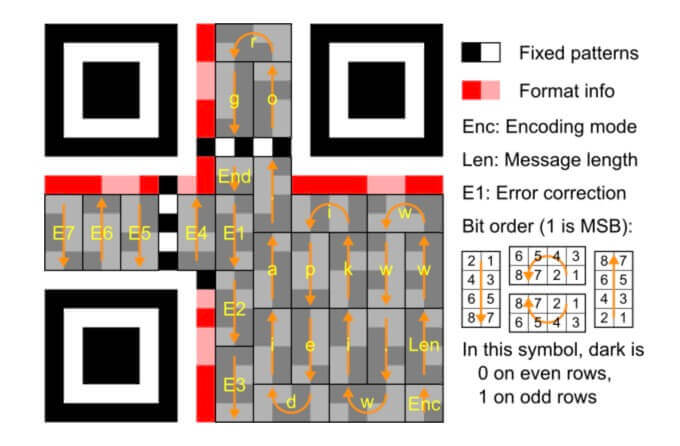
以下是一个版本2,纠错级别为M的二维码数据区示意图,先填充数据码,数据码填充完再填充纠错码,D开头的是数据码,E开头为纠错码
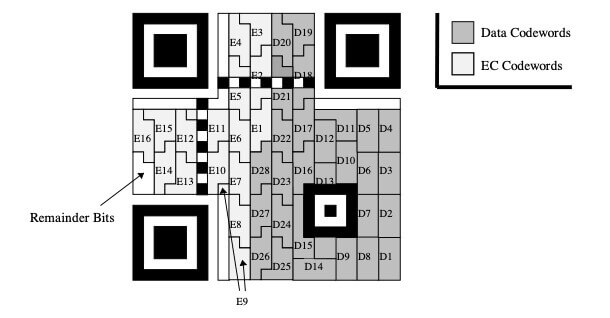
7、掩码:第4点讲到过,填充完数据区后,黑白点可能不均衡,会有大面积空白或黑色块,解码困难,掩码就是用来解决这个问题。将数据区的二进制数,和掩码的二进制数进行异或运算,最终得到的图形,才是我们看到的二维码。
结语
回到本文开头,还有一个问题:二维码能存储视频/音频吗?答案当然是可以的,因为最终都是转换成二进制,但是,二维码容量实际只有1KB,要存储视频/音频,只能说理论上可以。
觉得不错,点个star吧Github


