「杂题乱刷」洛谷 P2398
典题。
发现问题可以变为枚举 \(i\)，求出两两数 \(gcd\) 为 \(i\) 的个数，但是这样还是 \(O(n^2)\) 的。
然后可以将两边同时除以 \(i\)，原式变为
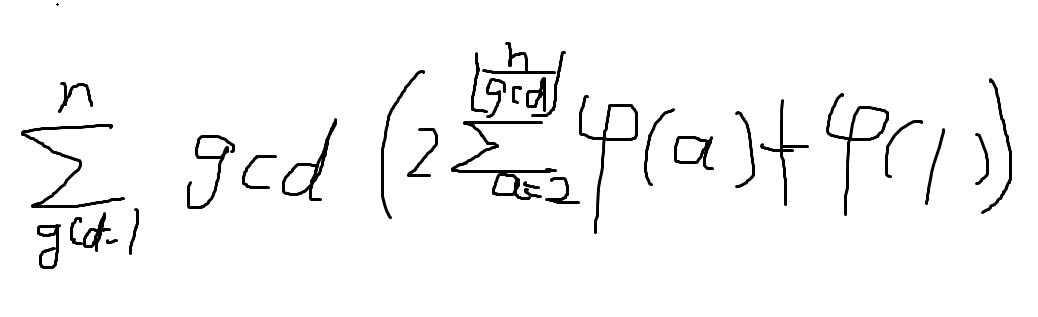
暴力筛复杂度是 \(O(n\log_2(n))\) 的，加个前缀和时间复杂度为 \(O(n)\)。
点击查看代码
/*
Tips:
你数组开小了吗？
你MLE了吗？
你觉得是贪心，是不是该想想dp？
一个小时没调出来，是不是该考虑换题？
*/
#include<bits/stdc++.h>
using namespace std;
#define map unordered_map
#define forl(i,a,b) for(register long long i=a;i<=b;i++)
#define forr(i,a,b) for(register long long i=a;i>=b;i--)
#define forll(i,a,b,c) for(register long long i=a;i<=b;i+=c)
#define forrr(i,a,b,c) for(register long long i=a;i>=b;i-=c)
#define lc(x) x<<1
#define rc(x) x<<1|1
#define mid ((l+r)>>1)
#define cin(x) scanf("%lld",&x)
#define cout(x) printf("%lld",x)
#define lowbit(x) x&-x
#define pb push_back
#define pf push_front
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
#define QwQ return 0;
#define ll long long
#define ull unsigned long long
#define lcm(x,y) x/__gcd(x,y)*y
#define Sum(x,y) 1ll*(x+y)*(y-x+1)/2
ll t;
ll sum[100010],n,Sum,ans,pd[100010];
ll a[100010],k;
void INIT(ll n)
{
forl(i,2,n)
{
if(!pd[i])
a[++k]=i;
for(ll j=1;j<=k&&i*a[j]<=n;j++)
{
pd[i*a[j]]=1;
if(i%a[j]==0)
break;
}
}
}
void init()
{
sum[1]=1;
forl(i,2,100000)
{
if(!sum[i])
a[++k]=i,sum[i]=i-1;
for(ll j=1;j<=k && i*a[j]<=100000;j++)
{
if(i%a[j]==0)
{
sum[i*a[j]]=sum[i]*a[j];
break;
}
else
sum[i*a[j]]=sum[i]*sum[a[j]];
}
}
/* forl(i,1,n)
sum[i]=i;*/
/* forl(i,2,n)
{
sum[i]--;
llSum=0;
if(!pd[i])
{
pd[i]=1;
forll(j,i,n,i)
sum[j]-=++Sum-pd[j],pd[j]=1;
}
}*/
// forl(i,1,n)
// cout<<sum[i]<<endl;
}
void solve()
{
cin>>n;
// init();
forl(Gcd,1,n)
{
ll Sum=0;
forl(i,1,n/Gcd)
Sum+=sum[i]*(2-(i==1));
ans+=Sum*Gcd;
}
cout<<ans<<endl;
}
int main()
{
// INIT(100005);
init();
IOS;
t=1;
// cin>>t;
while(t--)
solve();
/******************/
/*while(L<q[i].l) */
/* del(a[L++]);*/
/*while(L>q[i].l) */
/* add(a[--L]);*/
/*while(R<q[i].r) */
/* add(a[++R]);*/
/*while(R>q[i].r) */
/* del(a[R--]);*/
/******************/
QwQ;
}
