手算推导BP神经网络

一、神经元

下图的蓝色区域被称为一个“感知机”(Perceptron), 感知机是对信息进行编码、压缩、集成、融合的计算机智能接口系统。

说白了，就是在输入端输入X1~X7这7个输入值，在感知机中乘以各自的权重矩阵、加上偏置值b后再放入激活函数f，最后输出结果y.

 

 

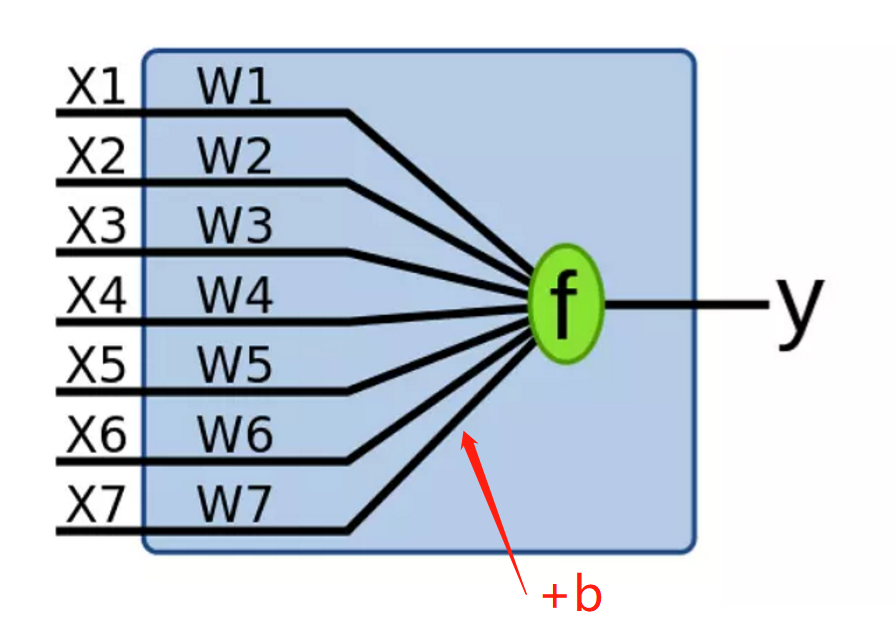
图中黄圈也代表了一个“感知机”，黄圈中进行了1.矩阵点乘后求和，2.加偏置值b，3.经过激活函数变换，这三项操作。

 

 

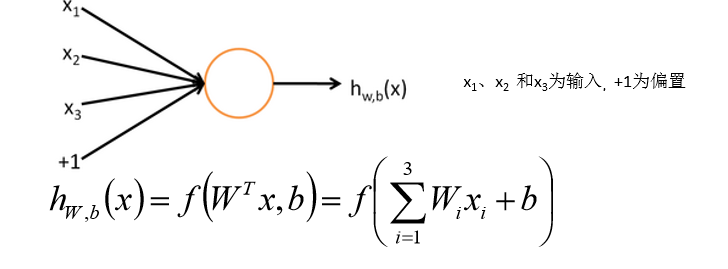
 常见的三种激活函数是sigmoid函数(又称S函数)、tanh函数和Relu函数，图像和公式见下：

 

 

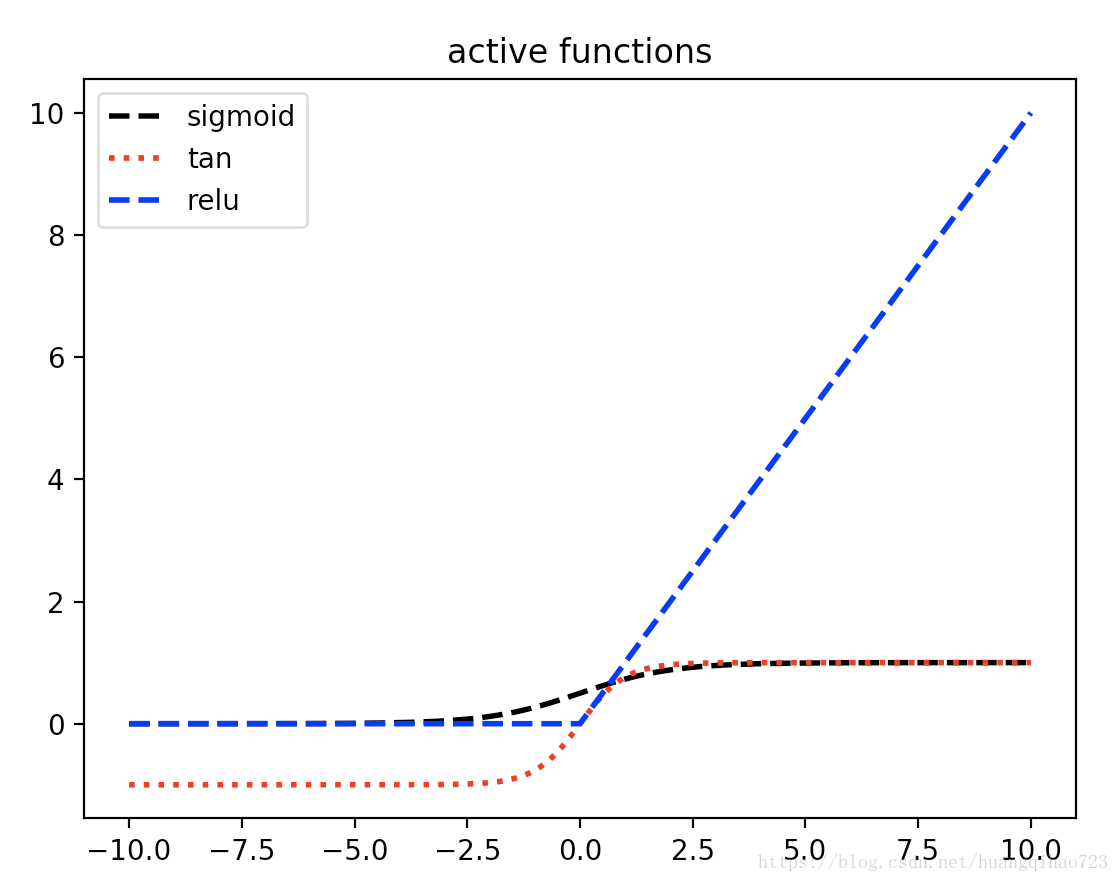
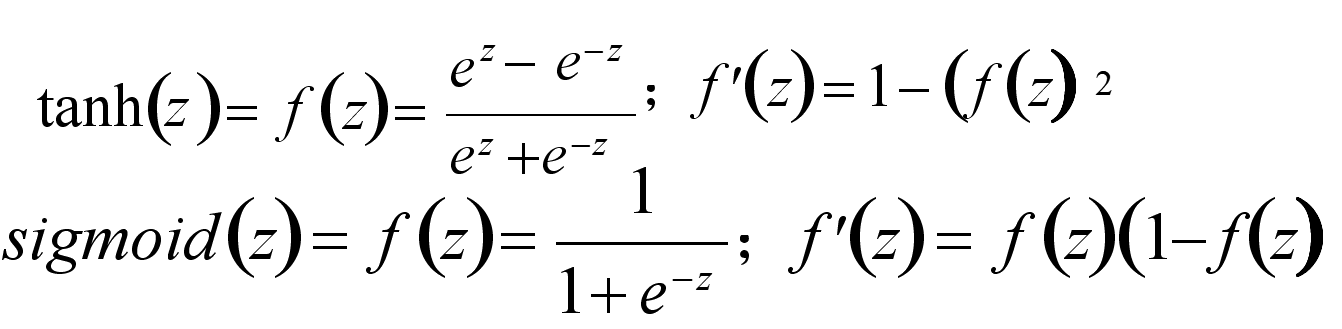
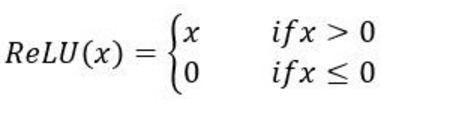
二、输入层、隐藏层、输出层

 

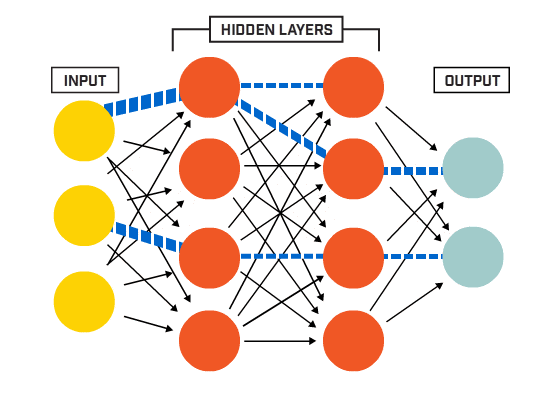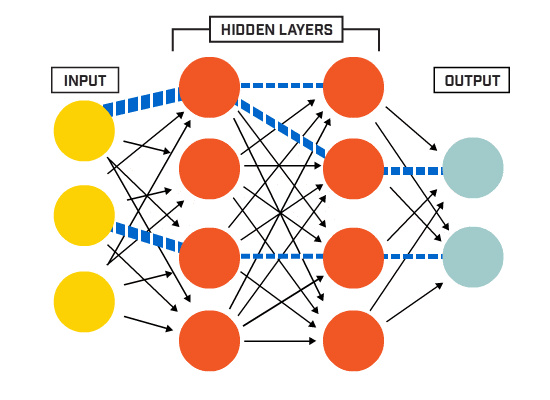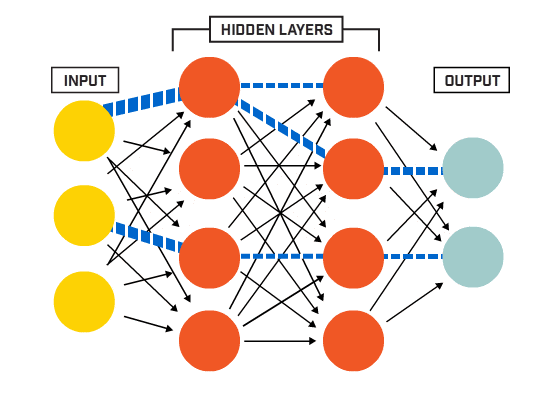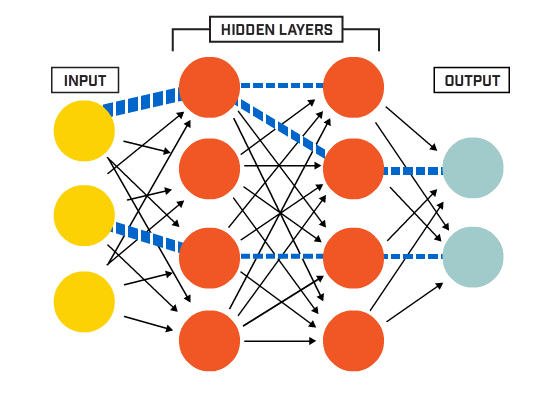
先求输出层的误差，而后倒推出隐藏层和输入层的误差：（d为真实值，O为最终预测值）

 

 

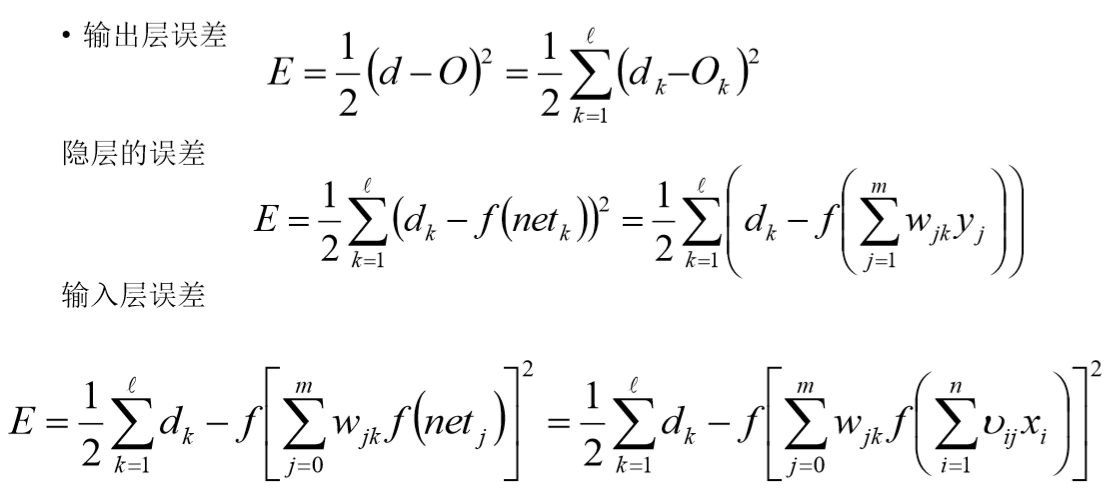
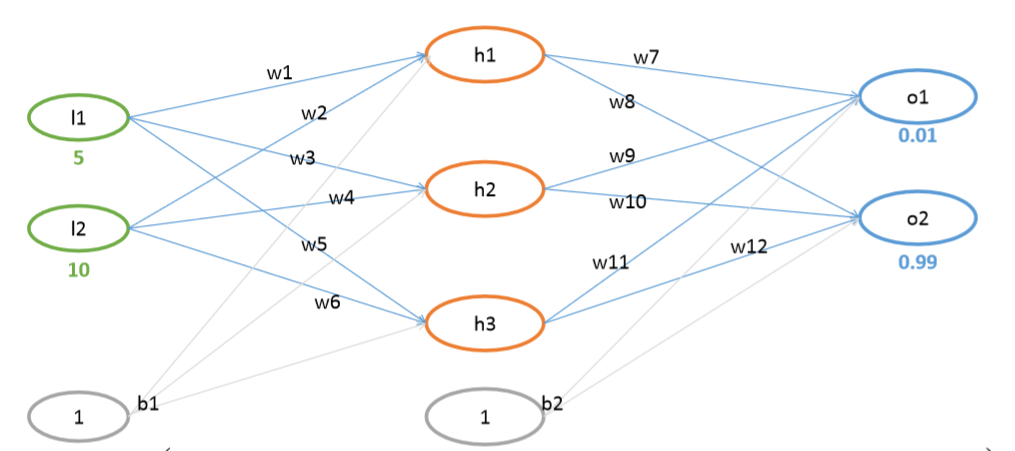
权重虚拟值：

偏置虚拟值：

 

 三、开始手推公式

 

对neth1 通过sigmoid激活函数之后，得到outh1，我们先看一下sigmoid函数的长什么样：（其实上面介绍激活函数时也画出来了）

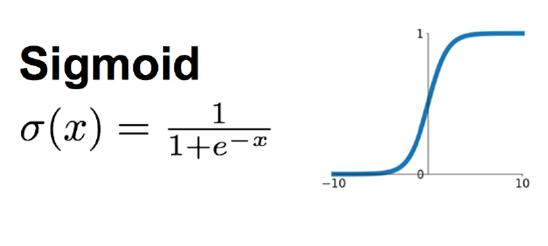
同理可得：

 

 

同理：

总损失:  

 

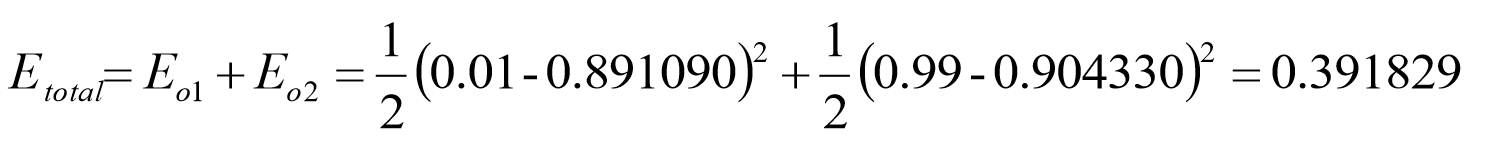
那么到此，结果的总损失已经算出，现在需要反向传播求偏导，以求出每一个参数对最终总损失的‘贡献’，为参数更新做准备。

 

 

                                               

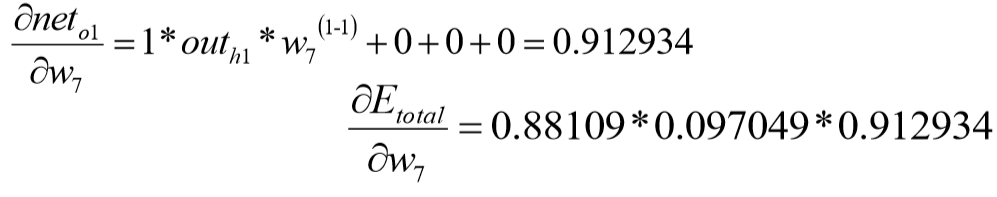
同理：

  

从而得到W1更新值：

        

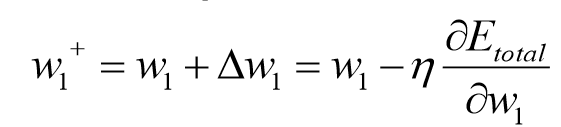
（注：1. 为学习率，即梯度下降中的步长，为超参数。

2.为什么学习率前是负号？因为目标函数一般都是下凹函数，偏导为正就需左移自变量，为负就需右移自变量）                                                                                              

同理可得到每一个W的更新值：

                

 

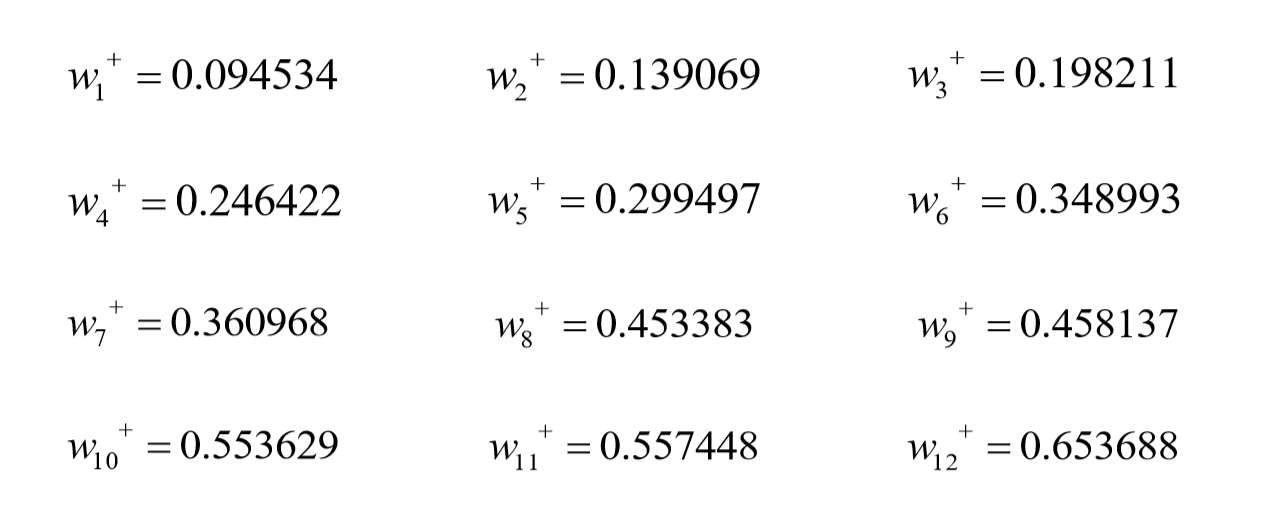
 顺便放在程序上跑一跑，可以发现进行这样的反向传播梯度更新的确会使最终结果越来越接近目标值。

（实际O1=0.01，O2=0.09）

 

最初的权重矩阵W0(随机赋值)是这样的：        

                      

迭代1000次（也就是更新1000次参数后）的权重矩阵W1000：