tensorflow:实战Google深度学习框架第四章02神经网络优化(学习率,避免过拟合,滑动平均模型)
1、学习率的设置既不能太小,又不能太大,解决方法:使用指数衰减法
例如:
假设我们要最小化函数 y=x2y=x2, 选择初始点 x0=5x0=5
1. 学习率为1的时候,x在5和-5之间震荡。
import tensorflow as tf TRAINING_STEPS = 10 LEARNING_RATE = 1 x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) x_value = sess.run(x) print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)
After 1 iteration(s): x1 is -5.000000. After 2 iteration(s): x2 is 5.000000. After 3 iteration(s): x3 is -5.000000. After 4 iteration(s): x4 is 5.000000. After 5 iteration(s): x5 is -5.000000. After 6 iteration(s): x6 is 5.000000. After 7 iteration(s): x7 is -5.000000. After 8 iteration(s): x8 is 5.000000. After 9 iteration(s): x9 is -5.000000. After 10 iteration(s): x10 is 5.000000.
2. 学习率为0.001的时候,下降速度过慢,在901轮时才收敛到0.823355
TRAINING_STEPS = 1000 LEARNING_RATE = 0.001 x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) if i % 100 == 0: x_value = sess.run(x) print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)
After 1 iteration(s): x1 is 4.990000. After 101 iteration(s): x101 is 4.084646. After 201 iteration(s): x201 is 3.343555. After 301 iteration(s): x301 is 2.736923. After 401 iteration(s): x401 is 2.240355. After 501 iteration(s): x501 is 1.833880. After 601 iteration(s): x601 is 1.501153. After 701 iteration(s): x701 is 1.228794. After 801 iteration(s): x801 is 1.005850. After 901 iteration(s): x901 is 0.823355.
3. 使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得不错的收敛程度
TRAINING_STEPS = 100 global_step = tf.Variable(0) LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True) x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) if i % 10 == 0: LEARNING_RATE_value = sess.run(LEARNING_RATE) x_value = sess.run(x) print "After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value)
After 1 iteration(s): x1 is 4.000000, learning rate is 0.096000. After 11 iteration(s): x11 is 0.690561, learning rate is 0.063824. After 21 iteration(s): x21 is 0.222583, learning rate is 0.042432. After 31 iteration(s): x31 is 0.106405, learning rate is 0.028210. After 41 iteration(s): x41 is 0.065548, learning rate is 0.018755. After 51 iteration(s): x51 is 0.047625, learning rate is 0.012469. After 61 iteration(s): x61 is 0.038558, learning rate is 0.008290. After 71 iteration(s): x71 is 0.033523, learning rate is 0.005511. After 81 iteration(s): x81 is 0.030553, learning rate is 0.003664. After 91 iteration(s): x91 is 0.028727, learning rate is 0.002436.
2、过拟合
要避免过拟合,解决办法:正则化
1. 生成模拟数据集。
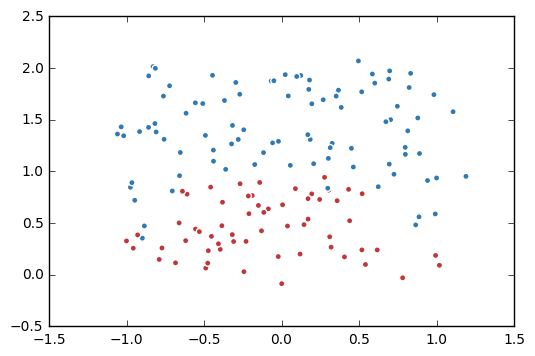
import tensorflow as tf import matplotlib.pyplot as plt import numpy as np data = [] label = [] np.random.seed(0) # 以原点为圆心,半径为1的圆把散点划分成红蓝两部分,并加入随机噪音。 for i in range(150): x1 = np.random.uniform(-1,1) x2 = np.random.uniform(0,2) if x1**2 + x2**2 <= 1: data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)]) label.append(0) else: data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)]) label.append(1) data = np.hstack(data).reshape(-1,2) label = np.hstack(label).reshape(-1, 1) plt.scatter(data[:,0], data[:,1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white") plt.show()
2. 定义一个获取权重,并自动加入正则项到损失的函数
def get_weight(shape, lambda1): var = tf.Variable(tf.random_normal(shape), dtype=tf.float32) tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var)) return var
3. 定义神经网络。
x = tf.placeholder(tf.float32, shape=(None, 2)) y_ = tf.placeholder(tf.float32, shape=(None, 1)) sample_size = len(data) # 每层节点的个数 layer_dimension = [2,10,5,3,1] n_layers = len(layer_dimension) cur_layer = x in_dimension = layer_dimension[0] # 循环生成网络结构 for i in range(1, n_layers): out_dimension = layer_dimension[i] weight = get_weight([in_dimension, out_dimension], 0.003) bias = tf.Variable(tf.constant(0.1, shape=[out_dimension])) cur_layer = tf.nn.elu(tf.matmul(cur_layer, weight) + bias) in_dimension = layer_dimension[i] y= cur_layer # 损失函数的定义。 mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size tf.add_to_collection('losses', mse_loss) loss = tf.add_n(tf.get_collection('losses'))
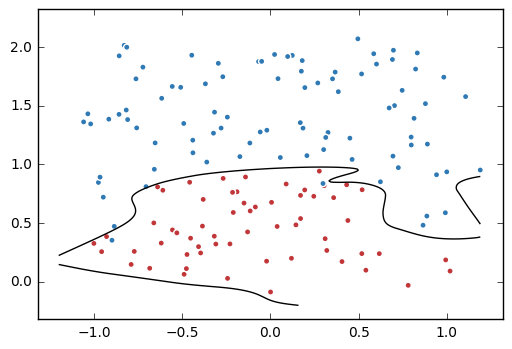
4. 训练不带正则项的损失函数mse_loss
# 定义训练的目标函数mse_loss,训练次数及训练模型 train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss) TRAINING_STEPS = 40000 with tf.Session() as sess: tf.global_variables_initializer().run() for i in range(TRAINING_STEPS): sess.run(train_op, feed_dict={x: data, y_: label}) if i % 2000 == 0: print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label}))) # 画出训练后的分割曲线 xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01] grid = np.c_[xx.ravel(), yy.ravel()] probs = sess.run(y, feed_dict={x:grid}) probs = probs.reshape(xx.shape) plt.scatter(data[:,0], data[:,1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white") plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1) plt.show()
After 0 steps, mse_loss: 2.315934 After 2000 steps, mse_loss: 0.054761 After 4000 steps, mse_loss: 0.047252 After 6000 steps, mse_loss: 0.029857 After 8000 steps, mse_loss: 0.026388 After 10000 steps, mse_loss: 0.024671 After 12000 steps, mse_loss: 0.023310 After 14000 steps, mse_loss: 0.021284 After 16000 steps, mse_loss: 0.019408 After 18000 steps, mse_loss: 0.017947 After 20000 steps, mse_loss: 0.016683 After 22000 steps, mse_loss: 0.015700 After 24000 steps, mse_loss: 0.014854 After 26000 steps, mse_loss: 0.014021 After 28000 steps, mse_loss: 0.013597 After 30000 steps, mse_loss: 0.013161 After 32000 steps, mse_loss: 0.012915 After 34000 steps, mse_loss: 0.012671 After 36000 steps, mse_loss: 0.012465 After 38000 steps, mse_loss: 0.012251
5. 训练带正则项的损失函数loss。
# 定义训练的目标函数loss,训练次数及训练模型 train_op = tf.train.AdamOptimizer(0.001).minimize(loss) TRAINING_STEPS = 40000 with tf.Session() as sess: tf.global_variables_initializer().run() for i in range(TRAINING_STEPS): sess.run(train_op, feed_dict={x: data, y_: label}) if i % 2000 == 0: print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_: label}))) # 画出训练后的分割曲线 xx, yy = np.mgrid[-1:1:.01, 0:2:.01] grid = np.c_[xx.ravel(), yy.ravel()] probs = sess.run(y, feed_dict={x:grid}) probs = probs.reshape(xx.shape) plt.scatter(data[:,0], data[:,1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white") plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1) plt.show()
After 0 steps, loss: 2.468601 After 2000 steps, loss: 0.111190 After 4000 steps, loss: 0.079666 After 6000 steps, loss: 0.066808 After 8000 steps, loss: 0.060114 After 10000 steps, loss: 0.058860 After 12000 steps, loss: 0.058358 After 14000 steps, loss: 0.058301 After 16000 steps, loss: 0.058279 After 18000 steps, loss: 0.058266 After 20000 steps, loss: 0.058260 After 22000 steps, loss: 0.058255 After 24000 steps, loss: 0.058243 After 26000 steps, loss: 0.058225 After 28000 steps, loss: 0.058208 After 30000 steps, loss: 0.058196 After 32000 steps, loss: 0.058187 After 34000 steps, loss: 0.058181 After 36000 steps, loss: 0.058177 After 38000 steps, loss: 0.058174

3、滑动平均模型
可以使模型有更好的表现
1. 定义变量及滑动平均类
import tensorflow as tf v1 = tf.Variable(0, dtype=tf.float32) step = tf.Variable(0, trainable=False) ema = tf.train.ExponentialMovingAverage(0.99, step) maintain_averages_op = ema.apply([v1])
2. 查看不同迭代中变量取值的变化。
with tf.Session() as sess: # 初始化 init_op = tf.global_variables_initializer() sess.run(init_op) print sess.run([v1, ema.average(v1)]) # 更新变量v1的取值 sess.run(tf.assign(v1, 5)) sess.run(maintain_averages_op) print sess.run([v1, ema.average(v1)]) # 更新step和v1的取值 sess.run(tf.assign(step, 10000)) sess.run(tf.assign(v1, 10)) sess.run(maintain_averages_op) print sess.run([v1, ema.average(v1)]) # 更新一次v1的滑动平均值 sess.run(maintain_averages_op) print sess.run([v1, ema.average(v1)])
[0.0, 0.0] [5.0, 4.5] [10.0, 4.5549998] [10.0, 4.6094499]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号