Harris角点检测

论文：C.Harris and M.Stephens. "A Combined Corner and Edge Detector. Proceedings of the 4th Alvey Vision Conference: pages147--151.

为什么需要检测角点

传统的边缘检测（如Sobel、Canny算法）虽然能找到图像中的线条，但这些线条上的点往往特征不够明显。而角点作为两条边缘的交点，具有以下独特优势：

• 方向不变性：无论从哪个角度观察，角点都能保持特征稳定性
• 唯一性：同一场景的不同图像中，角点更容易被重复检测
• 定位精确：像素级精度的位置检测能力

角点的直观理解

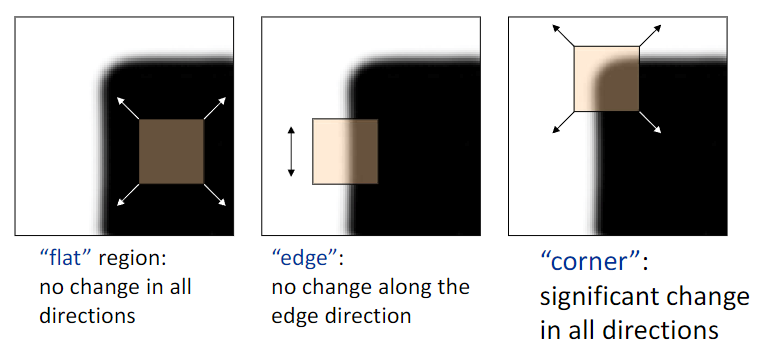
观察一个小窗口在图像上移动时的变化：

• 平坦区域：无论怎么移动，窗口内的像素几乎没有变化
• 边缘区域：沿边缘方向移动时变化很小，但垂直边缘方向移动时变化剧烈
• 角点区域：无论向哪个方向移动，窗口内的像素都会发生明显变化

所以，角点的本质特征是：在多个方向上具有显著的局部变化。

如何用数学方法描述这样的点？

数学建模

我们用一个能量函数来量化窗口移动带来的变化：

\[E(u, v)=\sum_{x, y} w(x, y)[I(x+u, y+v)-I(x, y)]^{2} \]

\(I(x, y)\)表示图像，\([I(x+u, y+v)-I(x, y)]^{2}\)描述了窗口内像素变化量，与\(w(x, y)\)加权求和得到整个窗口内所有像素的变化。也就是当我把窗口移动(u,v)时，图中显示把红色框框移动到绿色虚线框框，整个窗口内的变化大小，由E(u,v)来描述。

其中权值项w(x,y)可以是全1矩阵，表示所有点一视同仁，如果用高斯矩阵，表示越靠近中心的点越重要。

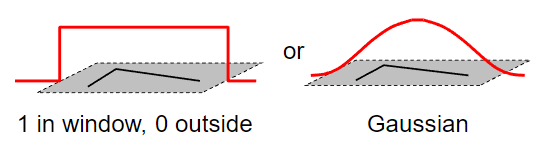
所以用数学语言描述刚才讲的“移动小窗口观察各个方向变化”，就是关注E(u,v)是如何随u,v变化。
换句话说就是观察E(u,v)随(u,v)这个方向上是如何变化的。

可以看到，当(u, v)等于(0, 0)时，窗口移动量为0，红框和绿框重合，没有差异，E(u,v)也就是0。

如何研究这种变化呢？

泰勒展开简化计算

显然，我们希望关注的是(u, v)在一个小范围变化时，E(u,v)的变化，也就是局部特征。范围大了，两个框框距离太远了，找出的变化就没什么意义了。此外，我们也更希望关注E(u,v)在(0,0)点附近的变化趋势，因为(0,0)点就是在我们当前点，我们要考虑在当前点附近E(u,v)的变化，从而判断当前点是否为角点。

另外，E(u,v)中的I(x,y)形式比较复杂，对于小位移情况如果直接求导计算会比较复杂。如果我们把它近似成一个多项式形式，就能大大简化我们的计算过程。同时还保留了局部的变化特性。

因此，我们将E(u,v)在(0，0)点进行二阶泰勒展开：

\[E(u, v) \approx E(0,0)+\left[\begin{array}{ll}u & v\end{array}\right]\left[\begin{array}{l}E_{u}(0,0) \\ E_{v}(0,0)\end{array}\right]+\frac{1}{2}\left[\begin{array}{ll}u & v\end{array}\right]\left[\begin{array}{ll}E_{u u}(0,0) & E_{u v}(0,0) \\ E_{u v}(0,0) & E_{v v}(0,0)\end{array}\right]\left[\begin{array}{l}u \\ v\end{array}\right] \]

其中：

\[E_{u}(u, v)=\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)] I_{x}(x+u, y+v)\]

\[E_{uu}(u, v)=\sum_{x, y} 2 w(x, y)I_x(x+u, y+v)I_x(x+u,y+v)+\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)]I_{xx}(x+u,y+v) \]

\[E_{uv}(u, v)=\sum_{x, y} 2 w(x, y)I_y(x+u, y+v)I_x(x+u,y+v)+\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)]I_{xy}(x+u,y+v) \]

我们把(0,0)带进去可得：

\[E(0,0)=0\]

\[E_{u}(0,0)=0\]

\[E_{v}(0,0)=0\]

\[E_{u u}(0,0)=\sum_{x, y} 2 w(x, y) I_{x}(x, y) I_{x}(x, y)\]

\[E_{v v}(0,0)=\sum_{x, y} 2 w(x, y) I_{y}(x, y) I_{y}(x, y)\]

\[E_{u v}(0,0)=\sum_{x, y} 2 w(x, y) I_{x}(x, y) I_{y}(x, y)\]

简化可得：

\[E(u, v) \approx [u\ v] M\begin{bmatrix}u\\v\end{bmatrix} \]

其中：

\[M=\sum_{x, y} w(x, y)\begin{bmatrix}I_{x}^{2}&I_{x}I_{y}\\I_{x}I_{y}&I_{y}^{2}\end{bmatrix} \]

\[M=\left[\begin{array}{cc} \sum I_{x} I_{x} & \sum I_{x} I_{y} \\ \sum I_{x} I_{y} & \sum I_{y} I_{y} \end{array}\right]=\sum\left[\begin{array}{c} I_{x} \\ I_{y} \end{array}\right]\left[I_{x} I_{y}\right]=\sum \nabla I(\nabla I)^{T} \]

理解M矩阵

此时，我们研究E(u,v)和u，v之间关系，就转化成研究M矩阵。
我们把E(u,v)的图画出来，大概是这个样子：

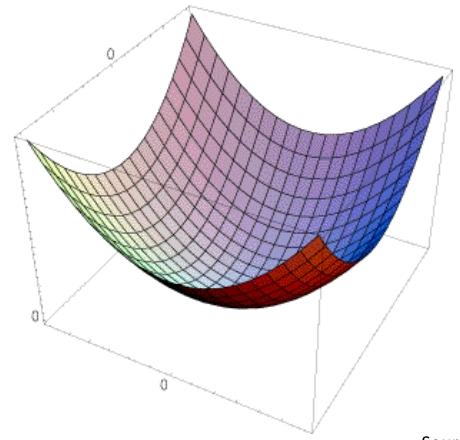
M决定了这个二次曲面的具体形状，也就决定了E(u,v)的变化情况。

由于二次曲面在其等值面上形状近乎一致，为了研究方便，我们用等值面对这个二次曲面进行研究。

\[\left[\begin{array}{ll}u & v\end{array}\right] M\left[\begin{array}{l}u \\ v\end{array}\right]= const \]

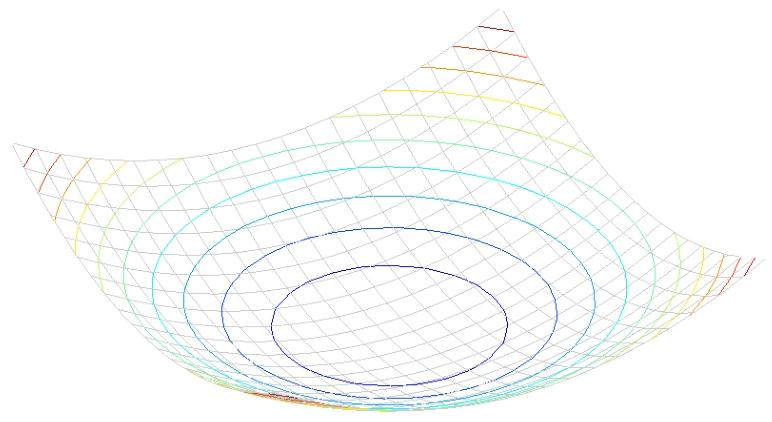
这个等值面是一个椭圆形。
我们对M进行对角化处理，就能定量的得到这个椭圆的一些性质。

\[M = R^{-1}\begin{bmatrix}\lambda_{1}&0\\0&\lambda_{2}\end{bmatrix}R \]

如下图，这里的λ1和λ2反映了椭圆的长轴和短轴，λmax越大，则该轴越短，从二次曲面上看，就是“爬升”的速度越快，且在这个方向上速度是最快的。反之，在λmin这个轴上，变化的最缓慢。
这个方向，是由R矩阵决定的，这是一个正交的旋转矩阵。也就是这个椭圆的旋转矩阵，也就描述的是E(u,v)在哪个方向上变化最快，哪个方向上变化最慢。

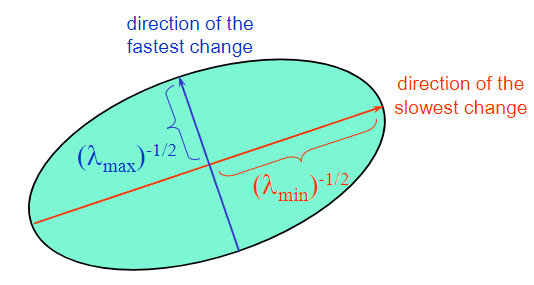
这是一张实际检测出的图片：

通常情况下，在我们检测角点的时候，是不关注旋转的，反正怎么旋转都不影响这是一个角点。因此，我们只要关注λ1和λ2的值。

利用M矩阵提取角点

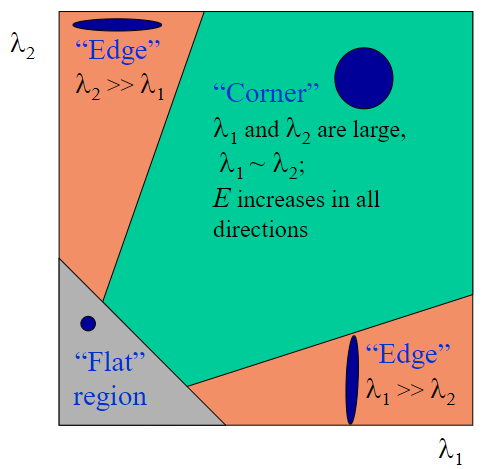
我们利用M矩阵得到λ1和λ2后，如果λ1远远大于λ2时，说明在一个方向上E(u,v)变化率远大于另一个方向，这应该是一条edge；如果λ1和λ2都很小，说明各个方向上变化率都小，这就是一个平坦的区域；如果λ1和λ2都很大，则该点在各个方向上变化率都很大，则该点更可能是一个角点。

Corner response function

为了更进一步的简化判断过程，我们采用这样一个响应方程来判断：

\[R = \det(M) - \alpha \text{trace}(M)^2=\lambda_{1}\lambda_{2}-\alpha(\lambda_{1}+\lambda_{2})^2 \]

通常取α = 0.04 到 0.06

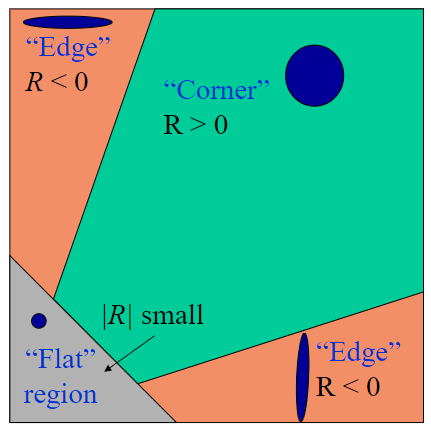
我们把上述分析套用到R中，如果λ1远远大于λ2时，λ1λ2应该是个小值，λ1+λ2应该是个大值，那么R小于0；如果λ1和λ2都很小，R的绝对值也是个小值；如果λ1和λ2都很大，则λ1λ2应该大于λ1+λ2，R大于0。

也就是我们可以通过R来判断该点是否为角点。

Harris角点检测步骤

1. 计算每个像素点的高斯导数。（利用高斯偏导核，使用Sobel算子获取Ix​,Iy​）
2. 在每个像素点周围的高斯窗口内计算二阶矩矩阵 M。
3. 计算角点响应函数 R。
4. 对 R 应用阈值处理。
5. 寻找响应函数的局部最大值（非最大化抑制） 。

算法总结

Harris 角点检测的优点在于：

• 旋转不变性：对图像旋转不敏感
• 灰度不变性：对光照变化有一定鲁棒性
• 计算高效：基于梯度的局部计算
  局限性：
• 对尺度变化敏感