poj 1066 Treasure Hunt

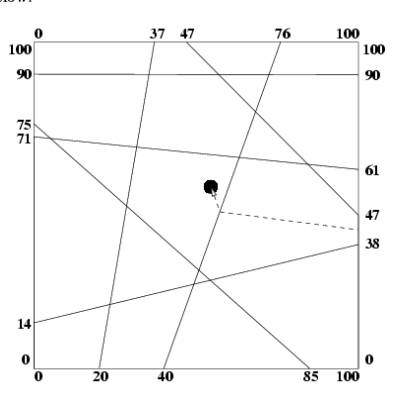
题意：一个正方形围墙内有一些交错的内墙，内墙的端点都在正方形上，在正方形内部有一个点，求从正方形外到这个点的最少要走的门数，门只能是线段的中点

方法：从一个点到终点不可能“绕过”围墙，只能穿过去，所以门是否开在中点是无所谓的，只要求四周线段中点到终点的线段与墙的最少交点个数即可。实际上，只需判断四周围墙的所有点与终点的连线与内墙的最少交点加一。

附上代码：

#include <iostream>
#include <math.h>

using namespace std;

#define eps 1e-8;

struct point{
    double x;
    double y;
};

struct line{
    point a;
    point b;
};

double xmult (point p0 ,point p1 ,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}
//判两点在线段异侧,点在线段上返回0
bool opposite_side (point p1 ,point p2 ,line l){
    return xmult(l.a,l.b,p1)*xmult(l.a,l.b,p2)<-eps;
}
//判两线段相交,不包括端点和部分重合
bool intersect_ex(line u, line v){
    return opposite_side(u.a,u.b,v)&&opposite_side(v.a,v.b,u);
}

int main()
{
    point p[100];
    line wall[35],link[1000];
    int n;
    while(cin >>n){
        int j=0;
        for(int i=0 ;i<2*n ;i++){
            cin >>p[i].x>>p[i].y;
            if(i%2==0)
                wall[i/2].a=p[i];
            else
                wall[i/2].b=p[i];
        }
        double x ,y;
        cin >>x>>y;
        for(int i=0 ;i<2*n ;i++){
            link[i].a.x=x,link[i].a.y=y;
            link[i].b=p[i];
        }
        int min=10000;
        for(int i=0 ;i<2*n ;i++){
            int count=0;
            for(int j=0 ;j<n ;j++){
                if(intersect_ex(link[i],wall[j]))
                    count++;
            }
            if(count<min)   min=count;
        }
        if(n==0)
            cout <<"Number of doors = 1"<<endl;
        else
            cout <<"Number of doors = "<<min + 1<<endl;
    }
}

版权声明：本文为博主原创文章，未经博主允许不得转载。