一 综述
坐标下降法属于一种非梯度优化的方法,它在每步迭代中沿一个坐标的方向进行搜索,通过循环使用不同的坐标方法来达到目标函数的局部极小值。
二 算法过程
假设目标函数是求解$f(x)$的极小值,其中$x=(x_1,x_2,\ldots,x_n)$是一个n维的向量,我们从初始点$x^0$开始($x^0$是我们猜想的一个初值)对k进行循环:
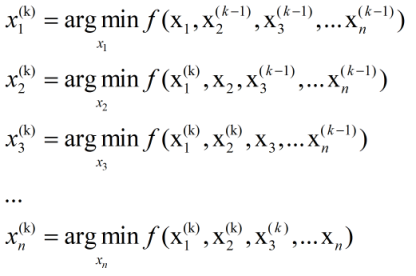
相当于每次迭代都只是更新$x$的一个维度,即把该维度当做变量,剩下的n-1个维度当作常量,通过最小化$f(x)$来找到该维度对应的新的值。坐标下降法就是通过迭代地构造序列$x^0,x^1,x^2,\ldots$来求解问题,即最终点收敛到期望的局部极小值点。通过上述操作,显然有:
$$f(x^0)\geq f(x^1)\geq f(x^2)\geq\ldots$$
=========================================================================
证明如下:
当$k=0$时,对应的$f(x)$的值为$f(x^0)=f(x_1^0,x_2^0,\ldots,x_n^0)$
由于$x_1^1=arg\min f(x_1,x_2^0,\ldots,x_n^0)$,所以$f(x_1^1,x_2^0,\ldots,x_n^0)\leq f(x_1^0,x_2^0,\ldots,x_n^0) = f(x^0)$,以此类推
所以$f(x_1^1,x_2^1,\ldots,x_n^0)\leq f(x_1^1,x_2^0,\ldots,x_n^0)\leq f(x_1^0,x_2^0,\ldots,x_n^0) = f(x^0)$
所以$f(x^1) =f(x_1^1,x_2^1,\ldots,x_n^1)\leq\ldots f(x_1^1,x_2^1,\ldots,x_n^0)\leq f(x_1^1,x_2^0,\ldots,x_n^0)\leq f(x_1^0,x_2^0,\ldots,x_n^0) = f(x^0)$
同理可得$f(x^2)\leq f(x^1)\leq f(x^0)$,命题得证。
======================================================================
相比梯度下降法而言,坐标下降法不需要计算目标函数的梯度,在每步迭代中仅需求解一维搜索问题,所以对于某些复杂的问题计算较为简便。但如果目标函数不光滑的话,坐标下降法可能会陷入非驻点。
三 注意事项
关于坐标下降法,有几点需要注意的:
1.坐标下降的顺序是任意的,不一定非得按照从$x^1\ldots x^n$的顺序来,可以是从1到n的任意排列。
2.坐标下降的关键在于一次一个地更新,所有的一起更新有可能会导致不收敛。
3.坐标上升法和坐标下降法的本质一样,只不过目标函数成为求$f(x)$的极大值了,每次迭代过程$min$变成$max$了。
参考:https://blog.csdn.net/u013802188/article/details/40476989/
https://blog.csdn.net/yMMxz/article/details/69396222





