关于极大似然估计的基本介绍,本文不再详细叙述(可参考:周志华——《机器学习》P149,陈希孺——《概率论与数理统计》P150 和其他资料)。文章的主要内容是我对极大似然估计的一些见解和我认为应该需要注意的一些点。以下是正文:
一.极大似然估计的简述
假设总体满足某种分布,且该分布的参数为(θ1,θ2,θ3,...θn),设该分布的具体形式为f(x;θ1,θ2,θ3,...θn)。其中x1,x2,x3,...xm为从这个总体中抽出的样本,那么,样本(x1,x2,x3,...xm)的分布为:

(这里的f实际上就是概率密度函数或者概率质量函数)
并记为
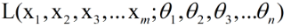
上述L就是我们所说的似然函数。而极大似然估计的目的就是从(θ1,θ2,θ3,...θn)所有可能的取值中,选出令似然函数L取值最大的那组。从这段话中我们可以得到以下几点结论:
1.极大似然估计的本质就是一种参数估计的方法,并且它是一种通过采样来对概率模型的参数进行估计的。(西瓜书上有同样的结论)
2.极大似然估计的一个极为重要的前提就是,我们假设的总体分布(同时也是采样获得的样本的分布)要与总体真实的分布尽可能的接近;或者说是估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布;如果对总体的分布一无所知的话,极大似然法就无能为力了。
3.实际上,以上的叙述中,还隐含了一个前提条件:对于这m个样本,它们都是独立同分布的。(例如,对于抛硬币问题,每次结果都是独立的)这是个很重要的前提,只有满足这个前提,似然函数才能写成这种连乘的形式,L才能称作是样本总体的似然函数。
二.对似然函数的通俗解释
1.似然函数的表示形式
关于似然函数的定义,可参考维基百科:https://zh.wikipedia.org/wiki/%E4%BC%BC%E7%84%B6%E5%87%BD%E6%95%B0
似然函数一般有两种表示方式:
第一种是:L(θ|x)
第二种是:L(x;θ)
因为有的资料是用的一种方式,有的资料用的是第二种方式,有时还可以写成L(θ),但无论哪种方式,它们实质都是一样的,即L(θ|x) = L(x;θ) = P(x|θ) 或者 L(θ|x) = L(x;θ) = P(x;θ)
2.似然函数的意义
对于p(x|θ)或者是p(x;θ):
(1)当x是变量,θ是已知量的时候,这个式子表示的是一个概率函数,即概率分布的参数取值为θ时,不同样本x出现的概率。
(2)当x是已知量,θ为变量的时候,这个式子表示的是一个似然函数,即概率分布的参数取不同值时,某个样本x出现的概率。
对于似然函数,也可以理解为:似然函数就是衡量当前模型参数对于已知样本集的解释情况(结合第三部分能更好的理解这句话)。
3.似然函数的实例
关于似然函数的实例,最经典的就是”抛硬币问题”了。对于这个问题,维基百科中叙述的已经很详细了,我此处只说明几个我认为比较重要的点:
(1)假设硬币正面朝上的概率PH = 0.5,投一次硬币正面朝上记为H的话,那么连续投币两次都正面朝上就表示为HH。那么,对于L(PH |HH) = p(HH|PH )=p(HH;PH ) = 0.25 ,对于这个取定的似然函数,在观测到两次投掷都是正面朝上时,PH = 0.5的似然性是0.25。
(注意此处的说法,此处说的参数取值的似然性,而不是当观测到两次正面朝上时PH = 0.5概率是0.25,因为这是p(PH |HH)所表示的含义)
(2)似然函数描述的是在观测到样本x时,参数取值的似然性,而极大似然估计就是找到合适的参数值来最大化这种似然性。
三.极大似然估计在机器学习问题中的应用
极大似然估计的核心就在于极大似然函数的表示(即对问题的建模)和求解,应用到机器学习问题中,概率模型就是所谓的学习器了,而训练集就相当于从总体中采样获得的有限样本集。所以,模型的训练过程实质就是参数估计的过程。但是,需要注意的一点是:似然函数中的这个参数,指的是你建立的概率模型的参数,但这个参数(实际上是个参数向量)与样本的概率分布的参数并不是完全相同的。那么该如何理解这个结论呢?这里我举例子进行说明:
对于”抛硬币问题",由于这个问题本身比较简单,对这个问题建模,所涉及的参数也就仅仅是样本x的概率分布的参数(即伯努利分布中的p);但在机器学习问题中,建模问题复杂化了,即建立的模型更复杂了,所涉及的参数业也就更多了,例如在逻辑回归(对数几率回归)中,此时的概率模型涉及的参数为w和b,虽然逻辑回归的本质是伯努利分布下的极大似然估计,但我们要明白此时的参数不再是伯努利分布中的呢个p了,而是w和b了。这一点我之前经常迷糊,所以这里着重强调一下。
==============================================================分割线====================================================
关于极大似然函数在机器学习中的应用,最具有代表性的模型就是逻辑回归和贝叶斯分类器了(通常用朴素贝叶斯分类器),下面结合这两个模型,以二分类为例,详细说明一下极大似然估计在ML中的应用。
1.逻辑回归(对数几率回归)中的极大似然估计
(1)首先,逻辑回归实际上是假设的样本的label的分布满足伯努利分布,即假设的总体分布满足伯努利分布。这里有两点需要注意:
第一点:
此处说的分布不再是样本x的分布,而是样本x对应的label即y的分布。
第二点:
y的分布满足的伯努利分布的话,设y=1出现的概率为p,这即P(y=1|x)的值为p,而P(y=1|x)又可以表示成关于w和b的函数,所以实际上影响模型结果的参数只有w和b了,要求解的只有w和b两个变量了。
注:此处假设的是样本x的label服从伯努利分布,并不是样本x分布,逻辑回归不需要知道样本满足何种分布。
(2)逻辑回归直接对后验概率p(y|x)进行建模,也就是说概率模型的似然函数应该是p(y|x;θ)的形式,《统计学些方法》中给出的逻辑回归的似然函数形式如下:
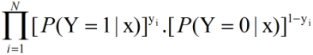
其中yi∈{0,1}。更及确切的说,应该是如下的形式:
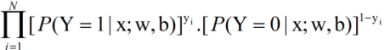
也就是说,逻辑回归的似然函数中考虑了所有样本的所属的类别,因为它是直接对P(y|x)进行建模的,它要找出所有的y,所以要考虑所有的样本。实际上,这个似然函数的本质就是伯努利分布下的概率密度函数。
2.贝叶斯分类器(以朴素贝叶斯为例)
(1)与逻辑回归这种判别模型不同的是,贝叶斯分类器直接是对x,y的联合概率进行建模的,而联合概率又由贝叶斯公式转化成一个先验概率和似然的乘积。具体形式如下:
P(x,y) = p(y).p(x|y)
其中p(y)称为类先验概率,p(x|y)称为“类条件概率”或者称为“似然”。
根据极大似然估计的定义,如果此时x中的属性都是离散属性的话,此时的模型同样也是假设的样本的label即y的分布满足伯努利分布,只不过此时的p为p(y=1)(以二分类为例的话);且xj| y也是满足伯努利分布的(需要注意的一点是,$p(y=c_k)$为p,$p(y \neq c_k)$为1-p;xj| y的话同理) 。但是此时的模型参数实际上就只有:
p(y = 1)、p(y = 0)、p(xj=ajl| y = 1)、p(xj=ajl| y = 0) 其中xj表示样本x的第j个属性,ajl表示第j个属性的第l个可能的取值。(前两个属于同一种参数,后两个属于同一种参数)
所以说,极大似然估计就是为了求解以上的参数。并且,《统计学习方法》P49给出了两种参数最终求解后的结果,现在书上大多是直接给的结果,并没有给出求解过程。
(2)那么,如何利用极大似然估计对上面两种参数进行求解呢?
可以参考:https://www.zhihu.com/question/33959624 或者 https://blog.csdn.net/zhulf0804/article/details/52474339
(3)根据两种参数的表示结果:
先给出似然函数的最终形式:
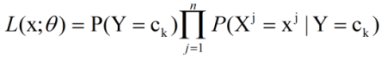
其中Xj表示X的第j个属性,而xj表示X第j个属性的取值。
再给出令似然函数去最大值时的参数的值:
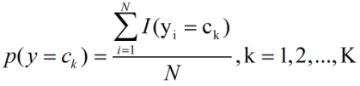
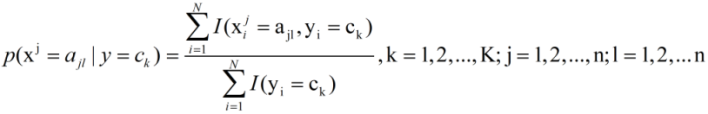
其中,I为指示函数,若括号内式子成立,则记为1,否则记为0。y=1和y=0可以分别表示成y=c1和y=c2。由此可见,模型的参数仅仅与训练样本有关,一旦样本给定了,模型的参数就确定了,这一点与逻辑回归是不同的。
另外,需要注意的是,上述的似然函数相当于包扩了所有的类别,参数也适用于所有的类别;可以理解成对每一个类别的样本,都建立了一个形式相同的似然函数。
最后,以上只是针对离散型属性,对于连续性属性,似然函数中还要考虑连续属性所服从的概率分布的参数。可以参考西瓜书P151的例子。




