一.题目链接:https://leetcode.com/problems/longest-substring-without-repeating-characters
二.题目大意:
给定一个字符串,返回它最长的无重复的子串的长度。
三.题解
该题目,我用了三种方法:
1.思路一:暴力解决,直接用两层for循环对目标字符串所有的子串进行判断。代码如下:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = s.length();
string str;//表示最长子串
int max_len = 0;
for(int i = 0; i < len; i++)
{
string t_str;//中间变量;
for(int j = i ; j < len; j++)
{
t_str = t_str + s[j];
if(isUnique(t_str) == 1)
{
if(t_str.length() > max_len)
max_len = t_str.length();
}
else
break;
}
}
return max_len;
}
//判断字符串是否包含重复元素(利用了哈希表,所以时间复杂度为O(n))
int isUnique(string s)
{
int len = s.length();
unordered_map<char,int> _map;
unordered_map<char,int>::iterator it;
for(int i = 0 ; i < len; i++)
{
it = _map.find(s[i]);
if(it == _map.end())
_map.insert(pair<char,int>(s[i],1));
else
return 0;
}
return 1;
}
};
isUnique()用于判断字符串是否包含重复的元素,由于用的是unordered_map(由哈希表实现,时间复杂度为O(1)),该函数的时间复杂度的为O(n);lengthOfLongestSubstring(string s)方法的时间复杂度为O(n2),故总的时间复杂度为O(n3),空间复杂度为O(n)。
提交结果:超时!
2.对方法一进行改,发现子串判断是否包含重复元素的过程可以在遍历过程中实现,所以就没必要单独定义一个方法了。代码如下:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = s.length();
string str;//表示最长子串
int max_len = 0;
for(int i = 0; i < len; i++)
{
string t_str;//中间变量;
unordered_map<char,int> _map;
unordered_map<char,int>::iterator it;
for(int j = i ; j < len; j++)
{
it = _map.find(s[j]);
if(it == _map.end())
{
t_str = t_str + s[j];
_map.insert(pair<char,int>(s[j],1));
if(t_str.length() > max_len)
max_len = t_str.length();
}
else
break;
}
}
return max_len;
}
};
这种方法,把unordered_map查询和插入的过程融合到for循环中,总的时间复杂度为O(n2),相比方法一时间上缩小了一个数量级。
提交结果:Accepted,耗时786ms.
3.看提交结果只打败了0.02%cpp提交。还可不可以再进行改进呢?
思路三:对于一个字符串,例如qpxrjxkltzyx,我们从头开始遍历时,如果遇到一个之前出现过的字符的话,例如:qpxrjx,那么从第一个x到第二个x的这段子串,一定不包含在我们的最终结果之中,我们需要记录的子串为:qpxrj;而且下一次的起始位置是第一个x之后的那个位置;这样指导最后一个字符;这实质可以看成一种贪心(子问题的性质决定了父问题的性质)。如图所示:
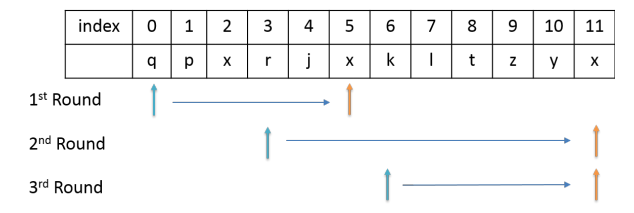
代码如下:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
vector<int>dict(256,-1);//此处的vector相当于一个哈希表
int max_len = 0;
int len = s.size();//string的size()方法和length()方法内部实现其实完全一样,只不过容器都有size()方法,此处是为了满足不同人的习惯
int start = -1;//起始位置
for(int i = 0; i < len; i++)
{ //遇到重复出现的字符,则start的位置变成重复的那个字符之前出现的位置
if(dict[s[i]] > start)
start = dict[s[i]];//本来start应该为dict[s[i]]+1的,但后面计算长度时,还需在加个1,相当于i-start+1,所以1相当于抵消了
max_len = max(max_len, i - start);//每次迭代长度都更新
dict[s[i]] = i;
}
return max_len;
}
};
需要注意的点都在注释中说明了,尤其需要注意的是start的赋值此处为了简便,把1去掉了;每次迭代长度更新相当于记录了当前子串的最大长度。此外start的初始值为-1,因为位置0处的字符也要考虑。i一直是增加的,只是start的位置在变化。
该算法的时间复杂度为O(n),空间复杂度为O(1),相比方法2,时间又缩短了一个数量级。
提交结果:Accepted,耗时18ms.
4.此外,如果本题要求的结果是最长无重复子串的话怎么办?可以设置两个标记s和e,用于记录每次更新max_len的i和start,最终的子串即以位置s开以位置e结尾的子串。
5.《剑指offer(第二版)》面试题48,给出了利用动态规划的思想求解,具体思路参考《剑指offer》,具体代码如下:
class Solution {
public:
int lengthOfLongestSubstring(string str) {
int max_len = 0;//最大值
int cur_len = 0;//以当前位置的字符结尾的不含重复字符的字符串的最大长度,对应f(i)
int pos[255] = {0};//记录字符上一次出现的位置
memset(pos,-1,sizeof(pos));
int len = str.size();
for(int i = 0; i < len; i++)
{
int pre_index = pos[str[i]];
if(pre_index < 0 || i - pre_index > cur_len)
cur_len++;
else
{
cur_len = i - pre_index;
}
pos[str[i]] = i;
if(cur_len > max_len)
max_len = cur_len;
}
return max_len;
}
};
此方法的时间复杂度同思路三一样,都是O(n),需要注意的是:
如果令dp[i]表示以第i个字符为结尾的不包含重复字符的子串的最长长度,那实际上cur_len这个变量就表示的是dp[i],即这段代码中没有显示的利用dp[i]的形式,因为没必要(我们求得是最大值,当前的结果只受前一个结果的影响,所以一个变量就能解决,没必要把所有的结果都存起来)。




