斯特林数及其相关知识和应用

目录

  引言
  自然幂，上升幂和下降幂
  第一类斯特林数
  第二类斯特林数
  第三类斯特林数
  三类斯特林数总结
  斯特林反演
  应用

引言

在组合数学，Stirling数可指两类数，第一类Stirling数和第二类Stirling数，都是由18世纪数学家James Stirling提出的。
Stirling数有两种，第一类Stirling数和第二类Stirling数，它们自18世纪以来一直吸引许多数学家的兴趣，如欧拉、柯西、西尔沃斯特和凯莱等。后来哥本哈根（Copenhagen）大学的尼尔森（Niels Nielsen，1865-1931）提出了"Stirlingschen Zahlen erster Art" (第一类Stirling数)和"Stirlingschen Zahlen zweiter Art" (第二类Stirling数)，首次把这两类数冠以「Stirling数」之名 。因为苏格兰数学家斯特林（J. Stirling, 1692-1770）首次发现这些数并说明了它们的重要性。
——来自于百度百科

此外，由于拉赫数与斯特林数关系密切，有时候也将拉赫数（Lah number）称为第三类斯特林数。

注：第二类斯特林数却在斯特林的相关著作和具体数学中被首先描述，同时也比第一类斯特林数常用得多。

自然幂，上升幂和下降幂

在介绍斯特林数之前，我先介绍一下自然幂，上升幂和下降幂，因为斯特林数的性质和这三种幂紧密相关。

自然幂符号及公式

$$m^n=\prod_{i=0}^{n-1} m$$

上升幂符号及公式

$$m^{\overline{n}}=\prod_{i=0}^{n-1}(m+i)$$

下降幂符号及其公式

$$m^{\underline{n}}=\prod_{i=0}^{n-1}(m-i)$$

上升幂和下降幂的转换

$$(-m)^{\overline{n}}=(-1)^nm^{\underline{n}}$$

$$(-m)^{\overline{n}}=(-1)^nm^{\underline{n}}$$

另外

其实自然幂和上升幂，自然幂和下降幂之间是可以相互转换的，在之后的前两类斯特林数的性质中会讲述。

第一类斯特林数

介绍

第一类斯特林数（斯特林轮换数）$\begin{bmatrix} n\\ m\end{bmatrix}$，表示将 $n$ 个两两不同的元素，划分成 $m$ 个互不区分的非空置换的方案数。

注：一个轮换是一个收尾相接的环形排列。两个可以通过旋转而互相得到的轮换是等价的（我们不认为两个可以通过翻转而相互得到的轮换等价）。

递推式

$$\begin{bmatrix} n\\ m\end{bmatrix}=\begin{bmatrix} n-1\\ m-1\end{bmatrix}+(n-1)\begin{bmatrix} n-1\\ m\end{bmatrix}$$

边界为：$\begin{bmatrix} n\\0\end{bmatrix}=[n=0]$ 。

运用组合意义证明：

• 新加入的元素独立作为一个置换，方案数为 $\begin{bmatrix} n-1\\ m-1\end{bmatrix}$ 。

• 新加入的元素加入现有的置换当中，因为对任意长度为 $l$ 的置换插入该置换的方案数为 $l$ ，当前置换总长为 $n-1$ ，所以方案数为 $(n-1)\begin{bmatrix} n-1\\ m\end{bmatrix}$ 。

根据加法原理，将两式相加即可得到递推式。

性质

1. $$n!=\sum_{i=0}^n\begin{bmatrix}n\\ i\end{bmatrix}$$

理解：对于一个排列 $P$ 我们可以将所有的 $(p_i, i)$ 连边，一个环则为一组轮换，每种排列一一每种置换。

证明：数学归纳法，请读者自行证明。

2. $$m^{\overline{n}}=\sum_{i=0}^n\begin{bmatrix} n\\i \end{bmatrix}m^i$$

证明：

• 显然，在 $n=0$ 的时候左右两边相等。
• 设 $n=k$ 的时候两边相等，即 $m^{\overline{k}}=\sum\limits_{i=0}^k\begin{bmatrix} k\\ i \end{bmatrix}m^i$。
• 则在 $n=k+1$ 时：

$$\begin{aligned} 左边&=m^{\overline{k+1}}\\ &=(m+k)m^{\overline{k}}\\ &=(m+k)\sum_{i=0}^k\begin{bmatrix} k\\ i \end{bmatrix}m^i \end{aligned}$$

$$\begin{aligned} 右边&=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i\\ &=\sum_{i=0}^{k+1}(\begin{bmatrix} k\\ i-1 \end{bmatrix}+k\begin{bmatrix} k\\ i \end{bmatrix})m^i\\ &=\sum_{i=0}^{k+1}\begin{bmatrix} k\\ i-1 \end{bmatrix}m^i+k\sum_{i=0}^{k+1}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\ &=\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^{i+1}+k\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\ &=(m+k)\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\&=左边 \end{aligned}$$

• 即 $m^{\overline{k+1}}=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i$

• 改命题由此得证。

3. $$m^{\underline{n}}=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i$$

证明：

• 由上式可得：

$$\begin{aligned} m^{\underline{n}}&=(-1)^n\cdot (-1)^{n}m^{\underline{n}}\\ &=(-1)^n(-m)^{\overline{n}}\\ &=\sum_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}(-m)^i\\ &=(-1)^n\sum_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}(-m)^i\\ &=(-1)^n\sum_{i=0}^n(-1)^{-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i\\ &=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i \end{aligned}$$

通项公式

第一类斯特林数目前没有实用的通项公式。

同一行第一类斯特林数的计算

由于 $O(n\log^2n)$ 的分治FFT的做法已经烂大街。

所以我们讲讲时间复杂度为 $O(n\log n)$ 的做法（虽然还是逃不过多项式）。

考虑构造生成函数 $F(x)^n=\prod\limits_{i=0}^{n-1}(x+i)=\prod\limits_{i=0}^{n}a_ix^i$ ，可以根据 $m^{\overline{n}}=\sum\limits_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}m^i$ 得到其中的 $a_i=\begin{bmatrix}n\\ i\end{bmatrix}$ 。

显然 $F(x)^{2n}=F(x)^nF(x+n)^n$ 。

$$\begin{aligned} F(x+n)^n&=\sum_{i=0}^n a_i(x+n)^i\\ &=\sum_{i=0}^n a_i\sum_{j=0}^n {i\choose j} x^jn^{i-j}\\ &=\sum_{i=0}^n \sum_{j=i}^n {j\choose i} x^in^{j-i} a_j\\ &=\sum_{i=0}^n \sum_{j=i}^n \frac{j!}{i!(j-i)!} x^in^{j-i}a_j\\ &=\sum_{i=0}^n\frac{1}{i!} (\sum_{j=i}^n a_jj! \frac{n^{j-i}}{(j-i)!}) x^i \end{aligned}$$

我们可以通过左半部分系数得到右半部分系数由此得到全部的系数。

时间复杂度: $T(n)=T(\frac n 2)+O(n\log n)=O(n\log n)$ 。

/**
 *    unicode: UTF-8
 *    name:    同一行第一类斯特林数的计算
 *    author:  wangjunrui
 *    created: 2022.07.03 周日 21:23:22 (Asia/Shanghai)
 **/
#include <algorithm>
#include <cstdio>
#define ll long long
#define lll __int128
#define ull unsigned ll
#define lowbit(x) (x & (-x))
template <typename T>
inline void read(T &x)
{
    x = 0;
    char s = (char)getchar();
    bool f = false;
    while (!(s >= '0' && s <= '9'))
    {
        if (s == '-')
            f = true;
        s = (char)getchar();
    }
    while (s >= '0' && s <= '9')
    {
        x = (x << 1) + (x << 3) + s - '0';
        s = (char)getchar();
    }
    if (f)
        x = (~x) + 1;
}
template <typename T, typename... T1>
inline void read(T &x, T1 &...x1)
{
    read(x);
    read(x1...);
}
template <typename T>
inline void ckmin(T &x, T y)
{
    if (x > y)
        x = y;
}
template <typename T>
inline void ckmax(T &x, T y)
{
    if (x < y)
        x = y;
}
using namespace std;
constexpr int N = 8e5 + 5;
constexpr int mod = 167772161;
constexpr int inv3 = 55924054;
inline ll quickpow(ll a, int b)
{
    ll res = 1;
    while (b)
    {
        if (b & 1)
            (res *= a) %= mod;
        (a *= a) %= mod;
        b >>= 1;
    }
    return res;
}
ll fac[N], ifac[N];
inline ll C(int n, int m)
{
    return fac[n] * fac[m] % mod * fac[n - m] % mod;
}
ll A[N], B[N];
int len, limit, rk[N];
inline void init(int all)
{
    len = 0, limit = 1;
    while (limit <= all)
    {
        limit <<= 1;
        ++len;
    }
    for (int i = 0; i < limit; ++i)
        rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
inline void NTT(ll *dp)
{
    for (int i = 0; i < limit; ++i)
        if (i < rk[i])
            swap(dp[i], dp[rk[i]]);
    for (int mid = 1; mid < limit; mid <<= 1)
    {
        ll gn = quickpow(3, (mod - 1) / (mid << 1));
        for (int j = 0; j < limit; j += mid << 1)
        {
            ll g = 1;
            for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
            {
                ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
                dp[i + j] = (x + y) % mod;
                dp[i + j + mid] = (x - y) % mod;
            }
        }
    }
}
inline void INTT(ll *dp)
{
    for (int i = 0; i < limit; ++i)
        if (i < rk[i])
            swap(dp[i], dp[rk[i]]);
    for (int mid = 1; mid < limit; mid <<= 1)
    {
        ll gn = quickpow(inv3, (mod - 1) / (mid << 1));
        for (int j = 0; j < limit; j += mid << 1)
        {
            ll g = 1;
            for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
            {
                ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
                dp[i + j] = (x + y) % mod;
                dp[i + j + mid] = (x - y) % mod;
            }
        }
    }
    ll inv = quickpow(limit, mod - 2);
    for (int i = 0; i < limit; ++i)
        (dp[i] *= inv) %= mod;
}
ll answer[N];
inline void solve(int n)
{
    if (n == 1)
    {
        answer[1] = 1;
        return;
    }
    int las = n / 2;
    solve(las);
    for (int i = 0; i <= las; ++i)
        A[las - i] = answer[i] * fac[i] % mod;
    ll power = 1;
    for (int i = 0; i <= las; ++i, (power *= las) %= mod)
        B[i] = power * ifac[i] % mod;
    init(las * 2);
    NTT(A), NTT(B);
    for (int i = 0; i < limit; ++i)
        (A[i] *= B[i]) %= mod;
    INTT(A);
    reverse(A, A + las + 1);
    for (int i = 0; i <= las; ++i)
        (A[i] *= ifac[i]) %= mod;
    fill(A + las + 1, A + limit, 0);
    fill(B + 0, B + limit, 0);
    init(n);
    NTT(answer), NTT(A);
    for (int i = 0; i < limit; ++i)
        (answer[i] *= A[i]) %= mod;
    INTT(answer);
    fill(A + 0, A + limit, 0);
    if (n & 1)
        for (int i = n; i >= 1; --i)
            answer[i] = (answer[i - 1] + (n - 1) * answer[i]) % mod;
}
signed main()
{
    int n;
    read(n);
    fac[0] = 1;
    for (int i = 1; i <= n; ++i)
        fac[i] = fac[i - 1] * i % mod;
    ifac[n] = quickpow(fac[n], mod - 2);
    for (int i = n; i >= 1; --i)
        ifac[i - 1] = ifac[i] * i % mod;
    if(n)
        solve(n);
    else
        answer[0] = 1;
    for (int i = 0; i <= n; ++i)
        printf("%lld ", (answer[i] + mod) % mod);
    putchar('\n');
    return 0;
}

同一列第一类斯特林数的计算

在路上了

第二类斯特林数

介绍

第二类斯特林数（斯特林子集数）$\begin{Bmatrix}n\\ m\end{Bmatrix}$ ，表示将 $n$ 个两两不同的元素，划分为 $m$ 个互不区分的非空子集的方案数。

递推式

$$\begin{Bmatrix}n\\ m\end{Bmatrix}=\begin{Bmatrix}n-1\\ m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\ m\end{Bmatrix}$$

边界为 $\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]$。

运用组合意义证明：

• 将新元素单独放入一个子集，方案数为 $\begin{Bmatrix} n-1\\ m-1\end{Bmatrix}$ 。

• 新将新元素放入一个现有的非空子集，方案数为 $m\begin{Bmatrix} n-1\\ m\end{Bmatrix}$ 。

根据加法原理，将两式相加即可得到递推式。

性质

1. $$m^n=\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\underline{i}}$$

证明：

• 显然，在 $n=0$ 的时候左右两边相等。
• 设 $n=k$ 的时候两边相等，即 $m^k=\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}}$。
• 则在 $n=k+1$ 时：

$$\begin{aligned} 左边&=m^{k+1}\\ &=m\cdot m^k\\ &=m\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}} \end{aligned}$$

$$\begin{aligned} 右边&=\sum_{i=0}^{k+1} \begin{Bmatrix}k+1\\ i \end{Bmatrix}m^{\underline i}\\ &=\sum_{i=0}^{k+1} (\begin{Bmatrix}k\\ i-1 \end{Bmatrix}+i\begin{Bmatrix}k\\ i \end{Bmatrix})m^{\underline i}\\ &=\sum_{i=0}^{k+1} \begin{Bmatrix}k\\ i-1 \end{Bmatrix}m^{\underline i}+\sum_{i=0}^{k+1}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\ &=\sum_{i=0}^{k} \begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline {i+1}}+\sum_{i=0}^{k}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\ &=\sum_{i=0}^{k} (m-i)\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}+\sum_{i=0}^{k}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\ &=m\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}}\\ &=左边 \end{aligned}$$

• 即 $m^{\overline{k+1}}=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i$

• 改命题由此得证。

2. $$m^n=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}}$$

证明：

• 由上式可得：

$$\begin{aligned} m^n&=(-1)^n(-m)^n\\ &=(-1)^n\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}(-m)^{\underline{i}}\\ &=(-1)^n\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}(-1)^im^{\overline{i}}\\ &=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}} \end{aligned}$$

通项公式

$$\begin{Bmatrix}n\\ m\end{Bmatrix}=\sum_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$$

证明：

我们用二项式反演。

令 $f_i$ 为表示将 $n$ 个两两不同的元素，划分为 $i$ 个互不相同的 非空子集 的方案数。

显然 $f_i=i!\begin{Bmatrix}n\\ i\end{Bmatrix}$ 。

考虑令 $g_i$ 为表示将 $n$ 个两两不同的元素，划分为 $i$ 个互不相同的子集 （可非空） 的方案数。

显然 $g_i=n^i$ 。

我们考虑 $f_i$ 其实就是 $g_i$ 去掉所有的空子集，则我们只要钦定 $g_i$ 中那些是非空子集就可以写出 $f_i$ 和 $g_i$ 的关系了:

$$g_i=\sum_{j=0}^i {i\choose j}f_j$$

根据二项式反演：

$$\begin{aligned} f_i&=\sum_{j=0}^i(-1)^{i-j}{i\choose j}g_j\\ &=\sum_{j=0}^i(-1)^{i-j}{i\choose j}j^n\\ &=\sum_{j=0}^i \frac{i!(i-1)^{i-j}j^n}{j!(i-j)!} \end{aligned}$$

$$\begin{Bmatrix}n\\ m\end{Bmatrix}=\frac{f_m}{m!}=\sum_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$$

同一行第二类斯特林数的计算

根据通项公式，可以发现这是卷积的形式，直接卷积计算即可。

/**
 *    unicode: UTF-8
 *    name:    同一行第二类斯特林数的计算
 *    author:  wangjunrui
 *    created: 2022.07.04 周一 23:35:00 (Asia/Shanghai)
 **/
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
#define lll __int128
#define ull unsigned ll
#define lowbit(x) (x & (-x))
template <typename T>
inline void read(T &x)
{
    x = 0;
    char s = (char)getchar();
    bool f = false;
    while (!(s >= '0' && s <= '9'))
    {
        if (s == '-')
            f = true;
        s = (char)getchar();
    }
    while (s >= '0' && s <= '9')
    {
        x = (x << 1) + (x << 3) + s - '0';
        s = (char)getchar();
    }
    if (f)
        x = (~x) + 1;
}
template <typename T, typename... T1>
inline void read(T &x, T1 &...x1)
{
    read(x);
    read(x1...);
}
template <typename T>
inline void ckmin(T &x, T y)
{
    if (x > y)
        x = y;
}
template <typename T>
inline void ckmax(T &x, T y)
{
    if (x < y)
        x = y;
}
using namespace std;
constexpr int N = 8e5 + 5;
constexpr int mod = 167772161;
constexpr int inv3 = 55924054;
inline ll quickpow(ll a, int b)
{
    ll res = 1;
    while (b)
    {
        if (b & 1)
            (res *= a) %= mod;
        (a *= a) %= mod;
        b >>= 1;
    }
    return res;
}
int n;
ll fac[N], ifac[N];
int limit, len, rk[N];
ll A[N], B[N];
inline void init(int all)
{
    len = 0, limit = 1;
    while (limit <= all)
    {
        limit <<= 1;
        ++len;
    }
    for (int i = 0; i < limit; ++i)
        rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
inline void NTT(ll *dp)
{
    for (int i = 0; i < limit; ++i)
        if (i < rk[i])
            swap(dp[i], dp[rk[i]]);
    for (int mid = 1; mid < limit; mid <<= 1)
    {
        ll gn = quickpow(3, (mod - 1) / (mid << 1));
        for (int j = 0; j < limit; j += mid << 1)
        {
            ll g = 1;
            for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
            {
                ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
                dp[i + j] = (x + y) % mod;
                dp[i + j + mid] = (x - y) % mod;
            }
        }
    }
}
inline void INTT(ll *dp)
{
    for (int i = 0; i < limit; ++i)
        if (i < rk[i])
            swap(dp[i], dp[rk[i]]);
    for (int mid = 1; mid < limit; mid <<= 1)
    {
        ll gn = quickpow(inv3, (mod - 1) / (mid << 1));
        for (int j = 0; j < limit; j += mid << 1)
        {
            ll g = 1;
            for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
            {
                ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
                dp[i + j] = (x + y) % mod;
                dp[i + j + mid] = (x - y) % mod;
            }
        }
    }
    ll inv = quickpow(limit, mod - 2);
    for (int i = 0; i < limit; ++i)
        (dp[i] *= inv) %= mod;
}
signed main()
{
    read(n);
    fac[0] = 1;
    for (int i = 1; i <= n; ++i)
        fac[i] = fac[i - 1] * i % mod;
    ifac[n] = quickpow(fac[n], mod - 2);
    for (int i = n; i >= 1; --i)
        ifac[i - 1] = ifac[i] * i % mod;
    for (int i = 0; i <= n; ++i)
    {
        A[i] = quickpow(i, n) * ifac[i] % mod;
        B[i] = (i & 1 ? -1 : 1) * ifac[i];
    }
    init(n * 2);
    NTT(A), NTT(B);
    for (int i = 0; i < limit; ++i)
        (A[i] *= B[i]) %= mod;
    INTT(A);
    for (int i = 0; i <= n; ++i)
        printf("%lld ", (A[i] + mod) % mod);
    putchar('\n');
    return 0;
}

同一列第二类斯特林数的计算

在路上了

第三类斯特林数

介绍

第三类斯特林数（拉赫数）$L(n, m)，通常指无符号拉赫数 $L(n, m)$ ，表示将含有 $n$ 个元素的集合拆分为 $m$ 个非空线性有序子集的方法数目。

注： $\{(1, 2, 3)\}\ne \{(2, 3, 1)\}$ ，$\{(1, 2), (3)\}\ne \{(3), (1, 2)\}$ 。

拉赫数可以通过上升幂与下降幂之间的转化来定义：

无符号拉赫数

$$m^{\overline{n}}=\sum\limits_{i=0}^nL(n, i)m^{\underline{i}}$$

$$m^{\underline{n}}=\sum\limits_{i=0}^n(-1)^{n-i}L(n, i)m^{\overline{i}}$$

有符号拉赫数

$$m^{\overline{n}}=(-1)^n\sum\limits_{i=0}^nL'(n, i)m^{\underline{i}}$$

$$m^{\underline{n}}=\sum\limits_{i=0}^n(-1)^{i}L'(n, i)m^{\overline{i}}$$

通项公式

无符号拉赫数

$$L(n, m)={n-1\choose m-1}\frac{n!}{m!}$$

有符号拉赫数

$$L'(n, m)=(-1)^nL(n, m)=(-1)^n{n-1\choose m-1}\frac{n!}{m!}$$

递推式

由通项公式可得

$$\begin{aligned}L(n, m)&=\frac{n-m+1}{m(m-1)}L(n, m-1)\\&=(n+m-1)L(n-1, m)+L(n-1, m-1)\end{aligned}$$

边界：
$L(n, 0)=0$，$L(1, 1)=1$

性质

下面都是拉赫数的通项公式得出来的

$$\begin{aligned}L(n, m)&={n-1\choose m-1} \frac{n!}{m!}\\&={n\choose m}\frac{(n-1)!}{(m-1)!}\\&={n\choose m}{n-1 \choose m-1}(n-m)!\end{aligned}$$

$$\begin{aligned}L(n, m)&={n-1\choose m-1} \frac{n!}{m!}\\&=\frac{n!(n-1)!}{m!(m-1)!(n-m)!}\\&=\left(\frac{n!}{m!}\right)^2\frac{m}{n(n-m)!}\end{aligned}$$

三类斯特林数总结

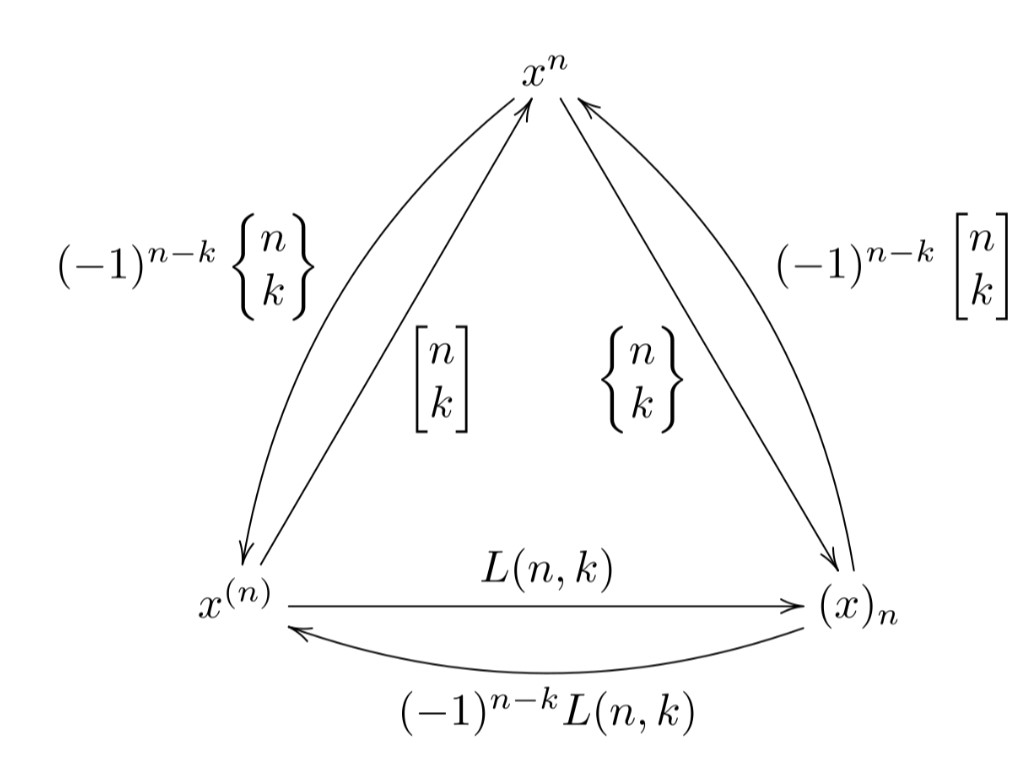
斯特林反演

原来第一类斯特林数和第二类斯特林数之间还能进行反演

前置知识

1. $$m^{\overline{n}}=\sum_{i=0}^n\begin{bmatrix} n\\i \end{bmatrix}m^i$$

2. $$m^{\underline{n}}=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i$$

3. $$m^n=\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\underline{i}}$$

4. $$m^n=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}}$$

具体证明见上面性质部分。

原理

$$\begin{aligned} m^n&=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}}\\ &=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\sum_{j=0}^i\begin{bmatrix} i\\ j \end{bmatrix}m^j\\ &=\sum_{i=0}^n m^i\sum_{j=i}^n(-1)^{n-j}\begin{Bmatrix}n \\ j\end{Bmatrix}\begin{bmatrix} j\\ i \end{bmatrix} \end{aligned}$$

• 由于这是一个恒等式，我们比对系数可得：

$$\sum_{i=m}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\begin{bmatrix} i\\ m \end{bmatrix}=[n=m]$$

2. 和上面的推式子一样：

$$\begin{aligned} m^{\underline{n}}&=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i\\ &=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\sum_{j=0}^i\begin{Bmatrix} i\\ j \end{Bmatrix}m^{\underline j}\\ &=\sum_{i=0}^n m^{\underline i}\sum_{j=i}^n(-1)^{n-j}\begin{bmatrix}n \\ j\end{bmatrix}\begin{Bmatrix} j\\ i \end{Bmatrix} \end{aligned}$$

• 由于这是一个恒等式，我们比对系数可得：

$$\sum_{i=m}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\begin{Bmatrix} i\\ m \end{Bmatrix}=[n=m]$$

由此我们就有两个非常对称的恒等式：

$$\sum_{i=m}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\begin{bmatrix} i\\ m \end{bmatrix}=[n=m]$$

$$\sum_{i=m}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\begin{Bmatrix} i\\ m \end{Bmatrix}=[n=m]$$

第一种形式

$$f_n=\sum_{i=0}^n \begin{Bmatrix}n \\ i\end{Bmatrix}g_i\Leftrightarrow g_n=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}f_i$$

证明：

$$\begin{aligned} g_n&=\sum_{i=0}^n g_i[n=i]\\ &=\sum_{i=0}^n g_i\sum_{j=i}^n(-1)^{n-j}\begin{bmatrix}n \\ j\end{bmatrix}\begin{Bmatrix} j\\ i \end{Bmatrix}\\ &=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\sum_{j=0}^i\begin{Bmatrix} i\\ j \end{Bmatrix}g_j\\ &=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}f_i \end{aligned}$$

第二种形式

证明同上：

$$f_n=\sum_{i=0}^n \begin{bmatrix}n \\ i\end{bmatrix}g_i\Leftrightarrow g_n=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}f_i$$

证明：

$$\begin{aligned} g_n&=\sum_{i=0}^n g_i[n=i]\\ &=\sum_{i=0}^n g_i\sum_{j=i}^n(-1)^{n-j}\begin{Bmatrix}n \\ j\end{Bmatrix}\begin{bmatrix} j\\ i \end{bmatrix}\\ &=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\sum_{j=0}^i\begin{bmatrix} i\\ j \end{bmatrix}g_j\\ &=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}f_i \end{aligned}$$

应用

在路上了

作者：蒟蒻wjr
欢迎任何形式的转载，但请务必注明出处。
限于本人水平，如果文章和代码有表述不当之处，还请不吝赐教。