2020年4月30日——Python

1.解题时，如果题目中的条件太紧，限制的太多，可以暂时忽略掉，根据题意，求出一般的数据模型时再去解题；相反的，如果题目中的条件太松，基本上没有什么太多的限制，可以适当的增加一些条件，等求出一般的数据模型时再去解题。

2.编写完dfs (深度优先搜索）时出现错误，如果觉得使用debug一步一步的去检查太麻烦，可以在程序中创建一个路径，将遍历的路径输出出来，这样会方便很多。

3.并不是所有的题都适合用暴力方法解决。

　　例如：长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左，有的朝右。

　　　　　每只蚂蚁都只能沿着杆子向前爬，速度是1厘米/秒。

　　           当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。

　　　　    这些蚂蚁中，有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。

　　　　    请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

 

 

　　　　这道题就不适合使用暴力方法解决。如果使用暴力方法去模拟感冒的蚂蚁，那就可能性太多了，很难实现，就算是实现出来，那程序对时间和空间的消耗是十分可怕的，所以  　　得换一条思路。

　　　　根据题意，去找题目中隐藏的规律：

　　　　　　　　

　　　　其中，箭头代表为蚂蚁，橘色的代表感冒的蚂蚁，经过模拟这几只蚂蚁到达杆子的两端时，可以发现：

　　　　　　

 

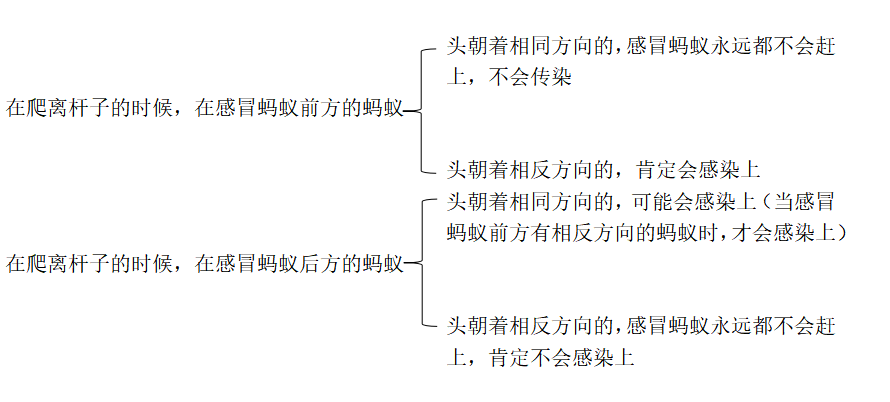
 　　　　经过这样的分析，这道题，就可以很好的进行解决了。

4.python中可以使用numpy库来进行创建数组：

import numpy as np
a=np.zeros((2,2))#创建二维（维度分别为2，2）的全零数组
c=np.arange(10000).reshape((10,10,10,10))#创建四维的0~9999的数组，其中（10，10，10，10）代表shape，指的是四维数组的各个维度，而10000就代表着0~9999

5.求斐波那契数列：

　　　定义：f(x)=1                   ...(x=1,2)

                     f(x)=f(x-1)+f(x-2)   ...(x>2)

　　（1）用代码直接实现：

 

n=int(input())#一直求到f(n)
a,b=1,1#代表着f(1)和f(2)
for i in range(3,n+1):
    t=a
    a=b
    b+=t
print(b)#f(n)=b　　

 

　　 　　思路是：

 

 

 　　　　(2)使用快速幂：

　　　　斐波那契数列有一个特性：

 　　　　通过上述公式，可以演变出：

 

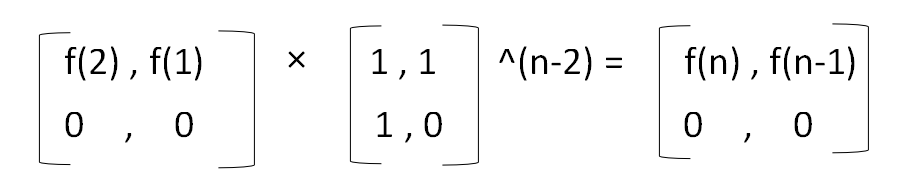
 　　　　使用这个方法实现程序，可以显著的提升时间性能，代码如下：

def mul(n,m):#将两个2*2的矩阵进行相乘
    a=[[0,0],[0,0]]
    a[0][0]=n[0][0]*m[0][0]+n[0][1]*m[1][0]
    a[0][1]=n[0][0]*m[0][1]+n[0][1]*m[1][1]
    a[1][0]=n[1][0]*m[0][0]+n[1][1]*m[1][0]
    a[1][1]=n[1][0]*m[0][1]+n[1][1]*m[1][1]
    return a
def mPow(n,m):#求n的m次幂
    a=[]#用来存储m的二进制数
    for i in bin(m).lstrip('0b'):
        a.append(i)
    e=[[1,0],[0,1]]#单位矩阵
    for i in reversed(a):
        if (int(i) and 1)==1:
            e=mul(e,n)
        n=mul(n,n)#按平方倍增
    return e
def fib(n):#计算f(n)
    a=[[1,1],[0,0]]#f(1)和f(2)
    b=[[1,1],[1,0]]
    c=mul(a,mPow(b,n-2))
    return c[0][0]

n=int(input())#求f(n)
"""
#第一种方法
a=1
b=1
t=0
if n[1]>=(n[0]+2):
    for i in range(3,n[0]+3):
        t=a
        a=b
        b+=t
    print(b%n[2]-1)
else:#m<n
    fibm=0
    for i in range(3,n[0]+3):
        t=a
        a=b
        b+=t
        if i==n[1]:
            fibm=b
    print(b%fibm%n[2]-1)
"""
#第二种方法
print(fib(n))