二叉排序树（BinarySortTree）

相关知识：

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

二叉树中的左右子树不可随意交换。

根节点：一棵树最上面的节点称为根节点。

父节点、子节点：如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点称为子 节点。

叶子节点：没有任何子节点的节点称为叶子节点。

兄弟节点：具有相同父节点的节点互称为兄弟节点

二叉排序树：

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树，他的特点如下：

• 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值
• 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值
• 左、右子树也分别为二叉排序树

二叉排序树的结构如下图所示：

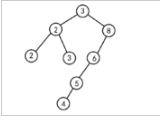
插入元素：

二叉排序树是一种动态树表。其特点是：树的结构通常不是一次生成的，首先执行查找算法，找出被插结点的父亲结点。判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。若二叉树为空。则首先单独生成根结点。

注：新插入的结点总是叶子结点。

查找元素：

若根结点的关键字值等于查找的关键字，成功；否则，若小于根结点的关键字值，递归查左子树；若大于根结点的关键字值，递归查右子树；若子树为空，查找不成功。

使用Java语言实现排序二叉树：

　　1.定义一个二叉树的封装节点类Node：

　　在Node类中，定义三个属性，int类型的value表示节点的值，Node类型的left表示节点的左子树，Node类型的right表示节点的右子树，并提供构造器和set、get方法。

package BST;
/**
 * 二叉树节点类
 * 属性：左子树，右子树，值
 * 构造器，修改器和访问器
 * @author ASUS
 *
 */
public class Node {
    private int value; //值
    private Node left; //左子树
    private Node right; //右子树
    
    //无参构造器
    public Node(){
        
    }
    
    //有参构造器
    public Node(Node left,Node right,int value){
        this.left=left;
        this.right=right;
        this.value=value;
    }
    
    //重载，一个参数构造器
    public Node(int value) {
        this.left=null;
        this.right=null;
        this.value=value;
    }

    //访问器和修改器
    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }
    
    
}

　　2.定义一个排序二叉树的工具类BSTTools

　　该类用于实现创建一个BST，在BST中遍历元素和在BST中删除指定元素等方法。

　　实现删除BST中指定元素的方法时，需要提供两个参数。分为三种情况，一种是要删除的元素key比根节点小，一种等于根节点，一种是比根节点大。

　　　　而当删除元素的key等于根节点时又分为三种情况：（假如删除的结点为p）

• 要删除的p结点是叶子结点，只需要修改它的双亲结点的指针为空
• 若p只有左子树或者只有右子树，直接让左子树/右子树代替p
• 若p既有左子树，又有右子树 ,用p左子树中最大的那个值代替p，重接其左子树

　　实现遍历时有两种方法：非递归遍历和递归遍历

　　　　采用递归的方法实现三种遍历，不仅代码简洁且容易理解，但其开销也比较大，而若采用非递归方法实现三种遍历，则要用栈来模拟实现（递归也是用栈实现的）

　　遍历二叉排序树时，有三种方法：

• 先序遍历，先遍历根节点，然后遍历左子树，再遍历右子树
• 中序遍历，先遍历左子树，然后遍历根节点，再遍历右子树（在BST中推荐使用该方法进行遍历，因为遍历结果呈现为各个节点按照从小到大依次排序）
• 后序遍历，先遍历左子树，然后遍历右子树，再遍历根节点

package BST;

import java.util.Stack;

public class BSTTools {
    private static Node root=null; //创建一个唯一的根节点
    
    /*该方法用于在BST中插入节点，参数为key
     * 步骤是：
     * 1.先定义插入节点的父节点，将root赋值给节点p
     * 2.节点p从根节点root开始查找，找到插入节点的相应位置
     * 3.在相应位置插入节点
     */
    public boolean insertNode(int key) {
        Node pNode=root;
        Node prev=null;//插入节点的父节点，设置其为null
        
        //找到插入节点的相应位置
        while(pNode!=null){
            prev=pNode;
            if (key<pNode.getValue()) {
                pNode=pNode.getLeft();
            }else if (key>pNode.getValue()) {
                pNode=pNode.getRight();
            }else{
                return true;
            }
        }
        
        //将节点插入到相应的位置
        if (root==null) {
            root=new Node(key);    
        }else if (key>prev.getValue()) {
            prev.setRight(new Node(key));
        } else {
            prev.setLeft(new Node(key));
        }
        return true;
    }
    
    /*中序遍历排序二叉树，有两中方法，递归遍历和非递归遍历,
     *中序遍历对二叉树来说就是将各个节点从小到大进行排序
     */
    
    /*非递归中序遍历二叉树
     *步骤是：
     *1，创建一个栈，从根节点开始遍历
     *2，利用循环来遍历，先左子树，后根节点，再右子树
     */
    public void sort() {
        //new一个stack的对象用来存储节点值，stack是堆存储，特点是：先进后出(FILO),跟栈类似
        Stack<Node> stack=new Stack<Node>();
        Node node=root;
        //从根节点开始遍历
        while(node!=null||!stack.isEmpty()){
            //如果根节点不为null，就循环先将左子树节点不断压入堆中  
            while (node!=null) {
                 stack.push(node);
                 node=node.getLeft();
            }
            //stack.pop（）方法表示移除并返回栈顶元素 
            node=stack.pop();
            //打印栈顶元素的值，即该节点的值
            System.out.println(node.getValue());
            //获得右子树
            node=node.getRight();
        }
    }
    
    /*递归中序遍历二叉树
     * 步骤是：
     * 利用递归方法来遍历，先左子树，后根节点，再右子树
     */
    public static void sort(Node node) {
        if (node==null) {
            return;
        } else {
            sort(node.getLeft());
            System.out.println(node.getValue());
            sort(node.getRight());
        }
    }
    
    //删除BST中的元素
    
    //从根节点开始查找相应的节点并删除
    public void delete(int key) {
        delete(root,key);
    }
    
    /*
     * 在BST中删除有三种情况：
     * 1.要删除的元素key比根节点小
     * 2.等于根节点
     * 3.比根节点大 
     */
    
    //从指定的节点开始查找相应的节点并删除
    public boolean delete(Node node,int key) {
        if(node==null){
            return false;
        }else{
            if (key==node.getValue()) {
                return deleteBST(node);
            } else if (key<node.getValue()) {
                return delete(node.getLeft(),key);
            } else {
                return delete(node.getRight(),key);
            }
        }
    }
    
    /*
     * 当删除的key和node.getValue相等时又分为三种情况：假如删除的结点为p
     * 1.要删除的p结点是叶子结点，只需要修改它的双亲结点的指针为空
     * 2.若p只有左子树或者只有右子树，直接让左子树/右子树代替p
     * 3.若p既有左子树，又有右子树 ,用p左子树中最大的那个值代替p，重接其左子树
     */
    private boolean deleteBST(Node node) {
        // TODO Auto-generated method stub
        Node temp=null;
        /*右子树空，只需要重接它的左子树 
         *如果是叶子结点，在这里也把叶子结点删除了 
         */
        if (node.getRight()==null) {
            temp=node;
            node=node.getLeft();
        //左子树空， 重接它的右子树
        } else if (node.getLeft()==null) {
            temp=node;
            node=node.getRight();
        //左右子树均不为空
        } else {
            temp=node;
            Node sNode=node;
            //转向左子树，然后向右走到“尽头”
            sNode=sNode.getLeft();
            while (sNode.getRight()!=null) {
                temp=sNode;
                sNode=sNode.getRight();
            }
            //将左子树最大的值代替被删除节点
            node.setValue(sNode.getValue());
            //将原来左子树最大值节点的左子树改为该节点父节点的右子树。
            temp.setRight(sNode.getLeft());
        }
        return true;
    }
}

　　3.定义一个测试类BinarySortTree：

　　该类主要用于测试BST。

package BST;

public class BinarySortTree {
    public static void main(String[] args) {
        BSTTools bstTools=new BSTTools();
        //构建的二叉树没有相同元素
        int[] num = {4,7,2,1,10,6,9,3,8,11,2, 0, -2}; 
        for (int i = 0; i < num.length; i++) {
            bstTools.insertNode(num[i]);
        }
        bstTools.sort();
        bstTools.delete(4);
        System.out.println("------------------");
        bstTools.sort();
    }
}