机器学习-单变量线性回归
(1) 说明:
假如我们希望通过房屋面积去预测一个地区的房屋价格,首先要收集这个地区的房屋数据,然后绘制成图像。图中的每一个点代表一个数据, 横坐标为房屋面积, 纵坐标为房屋价格。我们的目的就是根据训练数据去拟合一条直线。假设拟合的直线函数为:ℎ𝜃(𝑥) = 𝜃0 + 𝜃1𝑥,因为只有一个特征值房屋面积,因此这样的问题叫做单变量线性回归问题。

(2)代价函数

假如我们有这样一个训练集,截取前2个数据来看,我们首先设置𝜃0 和 𝜃1均等于1,那个可以算出偏差是 h(1) + h(2) = |1 + 1 * 2104 - 460| + |1 + 1 * 1416 - 232| = 2832;如果设置𝜃0 和 𝜃1均等于0.5,那么可以算出偏差值是 h(1) + h(2) = |0.5 + 0.5 * 2104 - 460| + |0.5+ 0.5 * 1416 - 232| = 1069;每取不同的𝜃0 和 𝜃1,会得到不同的偏差值,我们最终要计算的就是偏差值最小时候的𝜃0 和 𝜃1。由此引入了代价函数。m为训练集数量,y为训练集的输出变量。

(3)梯度下降
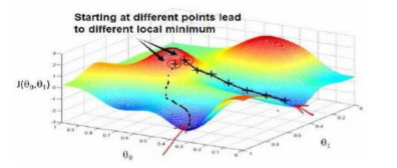
问题就转换成了求代价函数的最小值,梯度下降是一个用来求函数最小值的算法。如下图所示,取不同的𝜃0 和 𝜃1会对应不同的J(𝜃0, 𝜃1), 假设我们此时任意选择了一点point(𝜃0, 𝜃1),希望以最快的方式往下走,那么可以在垂直向下的方向画一条切线,由此来确定最佳的方向,走出一个距离之后,再确定下方向。。。以此类推最总会走到一个局部最优值。可以看到通过设定不同的点,得到得局部最优解可能会不同,但线性回归的代价函数是一个凸函数,只有一个全局最优解,无论从哪个初始点开始,最优解都是相同的。


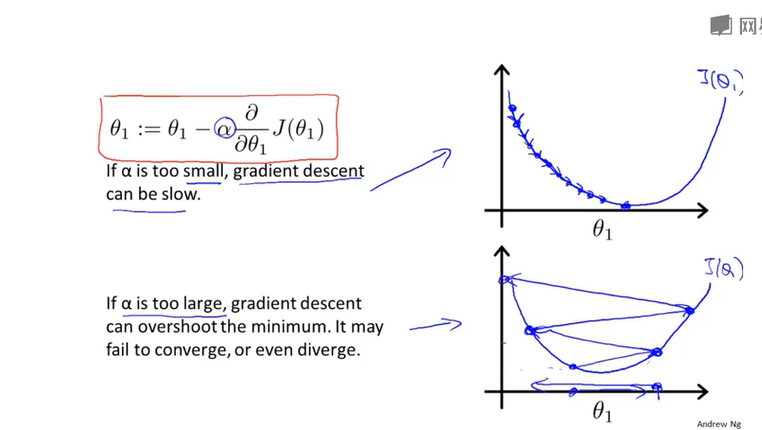
上面是原始公式,下面的是求完偏导之后的。其中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数(:=就是赋值)。我们需要同步更新𝜃0, 𝜃1,就是说我们要计算𝜃0, 𝜃1之后,再同时带入公式,而不是计算出其中一个就立马带入去计算下一个,下图中左边的是正确的做法。

(4)梯度下降中学习率的影响
从下面的第一个图可以看出,越往下图像斜率越小,走的也就越慢,当到达最低端图像斜率为0,𝜃值不再改变(𝜃=𝜃-0,但感觉理论上应该到不了0)表示收敛成功,但如果学习率选的偏大,直接迈过了最优值,反而会使结果发散,如第二个图。
(5)python代码实现:
1 def h(x): 2 global p1, p2 3 return p1 + p2 * x; 4 5 def J(x_data, y_data, type): 6 res = 0 7 for x, y in zip(x_data, y_data): 8 ext = x if type == 1 else 1 9 res += (h(x) - y) * ext 10 return res 11 12 13 14 #这里定义了很简单的直线, 结果可以看出是y = 1 + 3x 15 x_data = [1, 2, 3] 16 y_data = [4, 7, 10] 17 a = 0.1 18 p1 = p2 = 0; 19 m = len(y_data) 20 step = 500 21 for i in range(0, step): 22 tmpP1 = p1 - a / m * J(x_data, y_data, 0) 23 tmpP2 = p2 - a / m * J(x_data, y_data, 1) 24 p1, p2 = tmpP1, tmpP2 25 26 print(p1,p2) 27 #打印值:1.0006339781506417 2.9997211119234097 28 29 #预测当x=4时, y的值 30 print(h(4)) 31 #打印值:12.9995184258442
(6)函数直接实现:python库有对应的函数,可以直接调用
1 from sklearn.linear_model import LinearRegression 2 x_data = [[1], [2], [3]] 3 y_data = [4, 7, 10] 4 lr = LinearRegression() 5 lr.fit(x_data, y_data) 6 print(lr.predict([[4]]))



