推荐 - 3 - Deep & Cross Network for Ad Click Predictions - 1 - 论文学习
Deep & Cross Network for Ad Click Predictions
ABSTRACT
特征工程是许多预测模型成功的关键。然而，这个过程并不简单，经常需要手动的特性工程或穷举搜索。DNNs能够自动学习特征交互;然而，它们隐式地生成了所有的交互，并不能有效地学习所有类型的交叉特征。在本文中，我们提出了深度交叉网络(Deep & Cross Network, DCN)，它保留了DNN模型的优点，除此之外，它还引入了一种新的cross网络，更有效地学习某些bounded-degree特征交互。特别是，DCN在每一层都明确地应用了特征crossing，不需要人工特征工程，并且为DNN模型增加了可忽略不计的额外复杂性。实验结果表明，在CTR预测数据集和密集分类数据集上，该算法在模型精度和内存使用方面都优于现有的算法。
1 INTRODUCTION
点击率(CTR)预测是一个大规模的问题，对价值数十亿美元的在线广告行业至关重要。在广告业，广告商付钱给出版商，让他们在出版商的网站上展示广告。一种流行的付费模式是cost-per-click(CPC)模式，只有当点击发生时广告商才收费。因此，发行商的收入很大程度上依赖于准确预测点击率的能力。
识别预测特征，同时探索不可见或罕见的交叉特征是做出良好预测的关键。然而，web级推荐系统的数据大多是离散的和分类的，导致特征空间大而稀疏，对特征探索具有挑战性。这将大多数大规模系统限制为线性模型，如逻辑回归。
线性模型[3]简单，可解释，易于缩放;然而，他们的表达能力是有限的。另一方面，交叉特征已被证明在提高模型的表现力方面具有重要意义。不幸的是，它通常需要人工特性工程或穷举搜索来识别这些特性;此外，推广到不可见的特征交互是困难的。
在本文中，我们的目标是通过引入一种新的神经网络结构——cross network——来避免特定任务的特征工程，该网络明确地自动应用特征crossing。
cross网络由多层组成，其中最高程度的交互可由层深度确定。每一层都在现有层的基础上产生高阶交互作用，并保留了前一层的交互作用。我们将cross网络与深度神经网络(DNN)联合训练[10,14]。DNN有望捕获跨特征的非常复杂的交互作用;然而，与我们的cross网络相比，它需要比cross网络还要多近一个数量级的参数，且不能明确地形成交叉特征，可能无法有效地学习某些类型的特征交互。然而，将cross和DNN组件联合训练在一起，可以有效地捕获预测特征交互，并在Criteo CTR数据集上提供最先进的性能。
1.1 Related Work
由于数据集的大小和维数的急剧增加，许多基于embedding技术和神经网络的方法被提出，以避免广泛的任务特定的特征工程。
Factorization machines(FMs)[11,12]将稀疏特征投射到低维密集向量上，并从向量内积中学习特征交互。Field-aware factorization machines(FFMs)[7,8]进一步允许每个特征学习多个向量，其中每个向量与一个filed相关联。遗憾的是，FMs和FFMs的浅层结构限制了它们的表示能力。已有研究将FMs扩展到更高阶[1,18]，但缺点在于它们的大量参数产生了不期望的计算成本。由于embedding向量和非线性激活函数的存在，深度神经网络能够学习重要的高阶特征交互。残差网络[5]最近的成功使训练非常深入的网络成为可能。Deep Crossing[15]扩展了残差网络，通过叠加各种类型的输入实现自动特征学习。
深度学习的显著成功引出了对其表示能力的理论分析。已有研究[16,17]表明，在给定足够多的隐藏单元或隐藏层的情况下，DNN能够在一定的平滑假设下近似任意函数，达到任意精度。此外，在实践中，已经发现DNN在参数可行的情况下工作得很好。一个关键原因是，大多数实际使用的函数都不是任意的。
然而，剩下的一个问题是，DNNs是否确实是最有效的表示这些实际使用的函数的方法。在Kaggle竞赛中，许多胜出的解决方案中手工制作的特征都是low-degree的，格式明确且有效。另一方面，DNNs学习到的特征是隐式且高度非线性的。这为设计一个能够比通用DNN更有效、更明确地学习bounded-degree特征交互的模型提供了启示。
wide-and-deep[4]就是这种精神的典范。将cross特征作为线性模型的输入，与DNN模型联合训练线性模型。然而，wide-and-deep的成功取决于cross特征的正确选择，这是一个指数问题，目前还没有明确有效的解决方法。
1.2 Main Contributions
在本文中，我们提出了Deep & Cross Network(DCN)模型，该模型能够在稀疏和密集输入的情况下实现web规模的自动特征学习。DCN可以高效地捕获bounded degrees的有效特征交互，学习高度非线性的交互，不需要人工特征工程或穷举搜索，且计算成本低。
本文的主要贡献包括:
- 我们提出了一种新的cross网络，明确地在每一层上应用特征交叉，有效地学习bounded degrees的可预测的交叉特征，且不需要人工特征工程或穷举搜索。
- cross网络简单而有效。根据设计，最高多项式degree在每一层增加，并由层的深度决定。该网络由最大degree的所有交叉项组成，其系数各不相同。
- cross网络具有内存效率高、易于实现等优点。
- 我们的实验结果表明，在cross网络的情况下，DCN的logloss比DNN低，且参数数量也低了一个数量级。
论文的组织结构如下:第2节描述了Deep & Cross Network的体系结构。第三部分对cross网络进行了详细分析。第四节给出了实验结果。
2 DEEP & CROSS NETWORK (DCN)
在这一节中，我们描述了Deep & Cross Network(DCN)模型的体系结构。DCN模型首先是一个embedding和stacking层，然后是一个cross网络和一个并行的深度网络。接着是最后的combination层，将两个网络的输出结合起来。完整的DCN模型如图1所示。
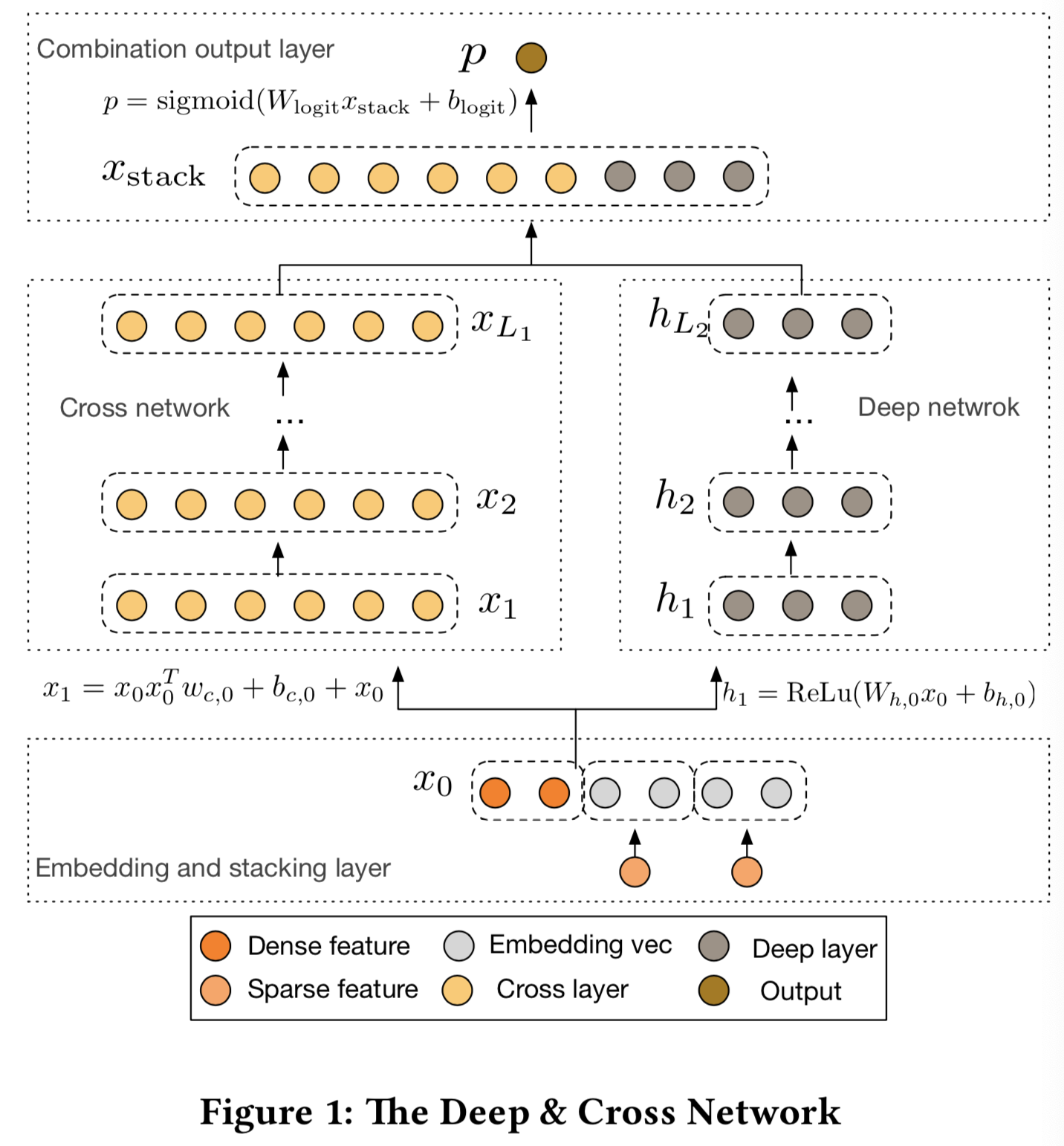
2.1 Embedding and Stacking Layer
考虑了带有稀疏和密集特征的输入数据。web规模的推荐系统，如CTR预测，输入大多数是类别特征，如"country=usa"。这样的特征经常编码为one-hot向量，如"[0,1,0]";但是，对于大的词汇表，这种方法经常会导致过度高维的特征空间。
为了减少维度，我们使用一个embedding过程去转变该二进制特征成实值密集向量（通常被叫成embedding向量）：
其中
是embedding向量，
为第i个类别的二进制输入，
是对应的embedding矩阵，将在网络中和其他参数一起优化，
分别是embedding大小和词汇表大小。
最后，我们将embedding向量和归一化后的密集特征
堆叠在一起得到一个向量：
然后将x0输入到网络中
2.2 Cross Network
这种新型cross网络的核心思想是有效地应用显式特征交叉。cross网络由cross层组成，每一层有如下公式:
其中
是分别表示来自第
个和第
个cross层的输出的列向量；
则是第层的权重和bias参数。每个cross层在每个特征交叉函数f后又把输入重新加回来，因此mapping函数
等于
残差。cross层的可视化可见图2:
High-degree Interaction Across Features. cross网络的特殊结构导致cross特征的degree随着层数的增加而增加。对于一个层的cross网络来说，最高的多项式degree为+1（就输入x0来说）。实际上，cross网络包含degree从1到+1的所有交叉项
。详细分析可见第3节。
Complexity Analysis. 
表示cross层的数量，d表示输入维度。然后cross网络的参数数量为：
cross网络的时间复杂度和空间复杂度在输入维数上是线性的。因此，与深度网络相比，cross网络引入的复杂性可以忽略不计，使得DCN的总体复杂性与传统的DNN保持在同一水平。这种效率得益于
的rank-one属性，它使我们能够在不计算或存储整个矩阵的情况下生成所有交叉项。
由于cross网参数较少，限制了模型的容量。为了捕捉高度非线性的交互，我们引入了一个并行的深度网络。
2.3 Deep Network
深度网络一个全连接的前馈神经网络，每一个深度层都是如下的公式：
其中
分别是第层和第层的隐藏层，
是第层的参数，f(.)是ReLU函数
Complexity Analysis. 为了简单起见，我们假设所有的深度层大小相同。设Ld表示深度层数，m表示深度层大小。则深度网络中的参数个数为：
2.4 Combination Layer
组合（combination）层将来自两个网络的输出连接起来，并将连接的向量输入到一个标准logits层中。
下面是一个两个类的分类问题的公式：
其中
分别是cross网络和深度网络的输出，
是组合层的权重向量，
。
损失函数是带有正则化项的log loss：
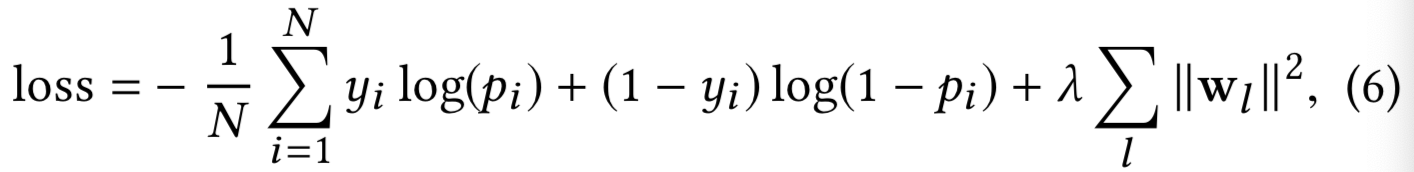
其中pi是等式5计算得到的概率，N是输入的总数，λ是L2正则化参数
我们联合训练两个网络，这样在训练时就允许每个单独的网络意识到另一个网络的存在。
3 CROSS NETWORK ANALYSIS
在本节中，我们对DCN的cross网络进行分析，以了解其有效性。我们提出了三个观点:多项式近似（polynomial approximation）、FMs泛化（generalization to FMs）和高效投影（efficient projection）。为了简单起见，我们假设bi = 0。
Notations. wj中的第i个元素表示为
。对于multi-index 
，我们定义
Terminology. 交叉项(monomial) 
的degree被定义为
。多项式的degree被该项的最大degree定义。
3.1 Polynomial Approximation
根据Weierstrass近似定理[13]，在一定光滑假设下的任意函数都可以用一个多项式近似到任意精度。因此，我们从多项式近似的角度来分析cross网络。特别地，cross网络以一种有效的、可表达的和能对真实数据集更好地泛化的方式来近似相同degree的多项式类。
详细研究了一个cross网络对相同degree多项式类的近似问题。用Pn(x)表示n次（degree）的多元多项式类:
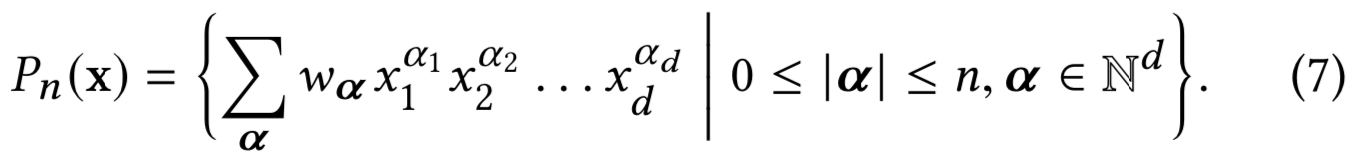
该类的每个多项式都有O(dn)个系数。我们证明，在只有O(d)参数的情况下，cross网络包含了所有出现在同次多项式中的交叉项，且每项的系数彼此不同。
Theorem3.1. 考虑一个层的cross网络，其i+1层定义为
。网络的输入为
，输出为
，参数为
。然后多元多项式
在以下的类中复制多项式：
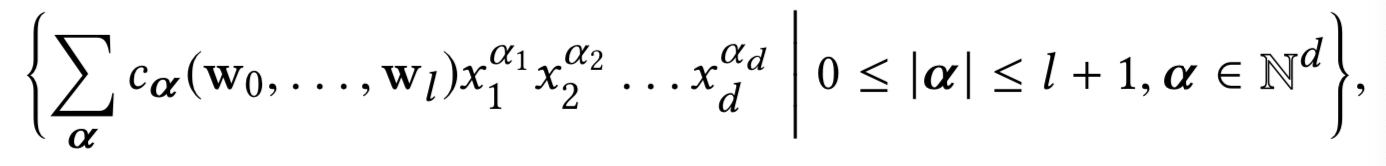
其中
，
是wi的常量独立项，
是multi-indices，
和
是指数
的所有排列的集合。
Theorem 3.1的证明在附录中。举例说明，
的系数为
，
。当=2时，
；当=3时，
######
Appendix: Proof of Theorem 3.1
PROOF. 其中i为值为0或1的multi-index向量，并且最后一个索引的值一定是1。对于multi-index 
，定义
首先使用归纳法证明：
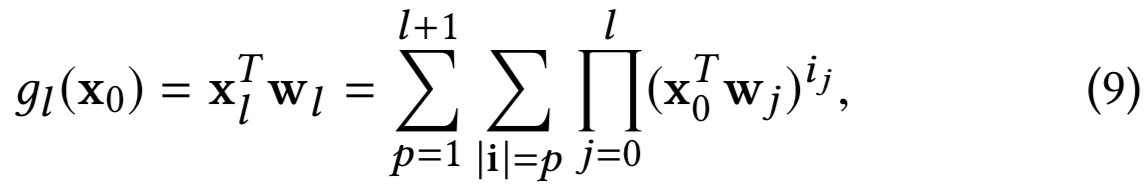
然后我们重写上面的形式来得到想要的claim。
Base case. 
归纳步骤。假设
：
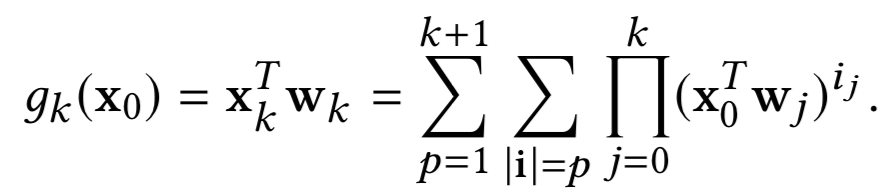
当
：
因为
仅包含
，所以
可以通过将所有出现在
的
替换为
来得到。所以
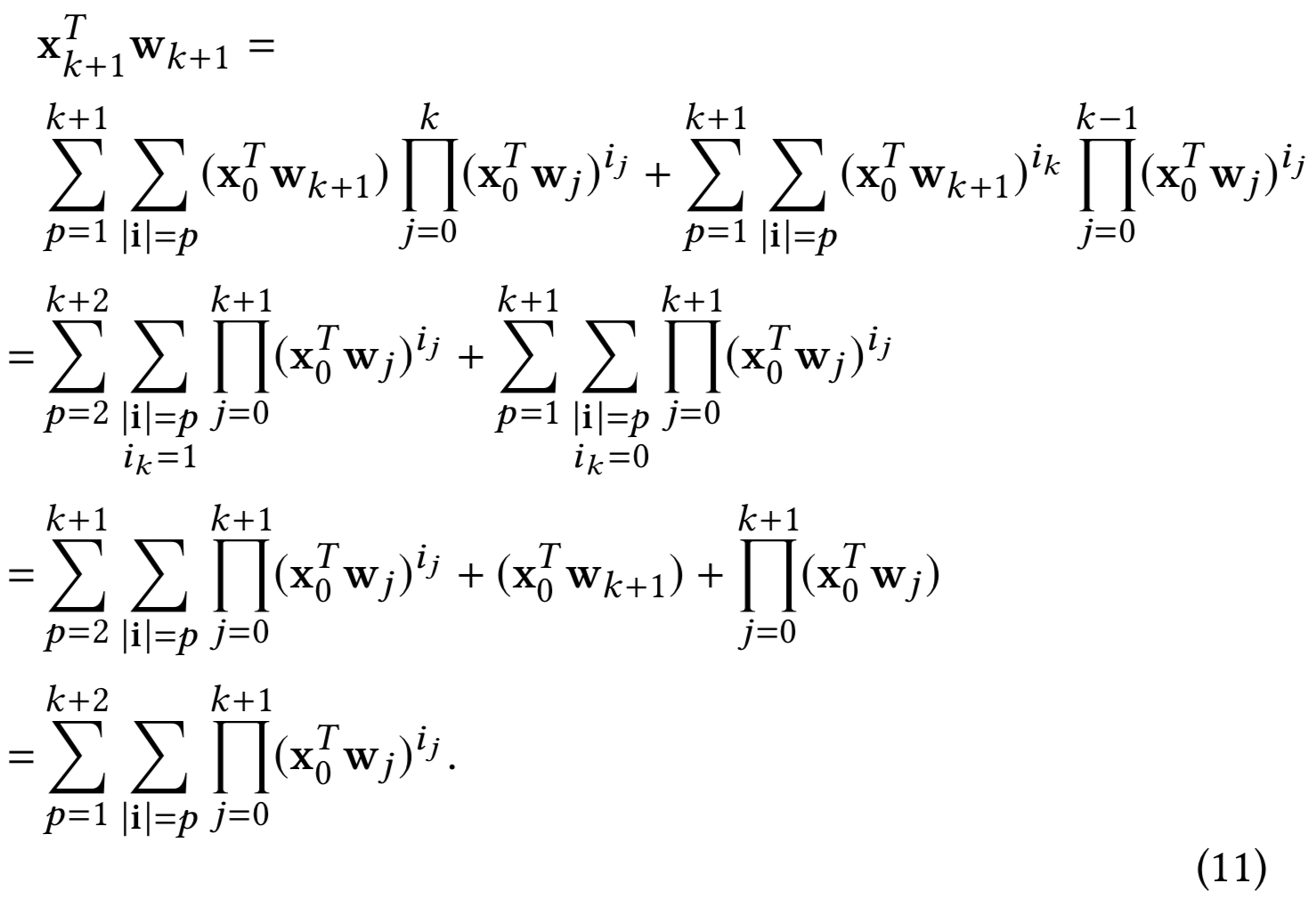
（等式11的解释：
第二个等号是怎么转的：
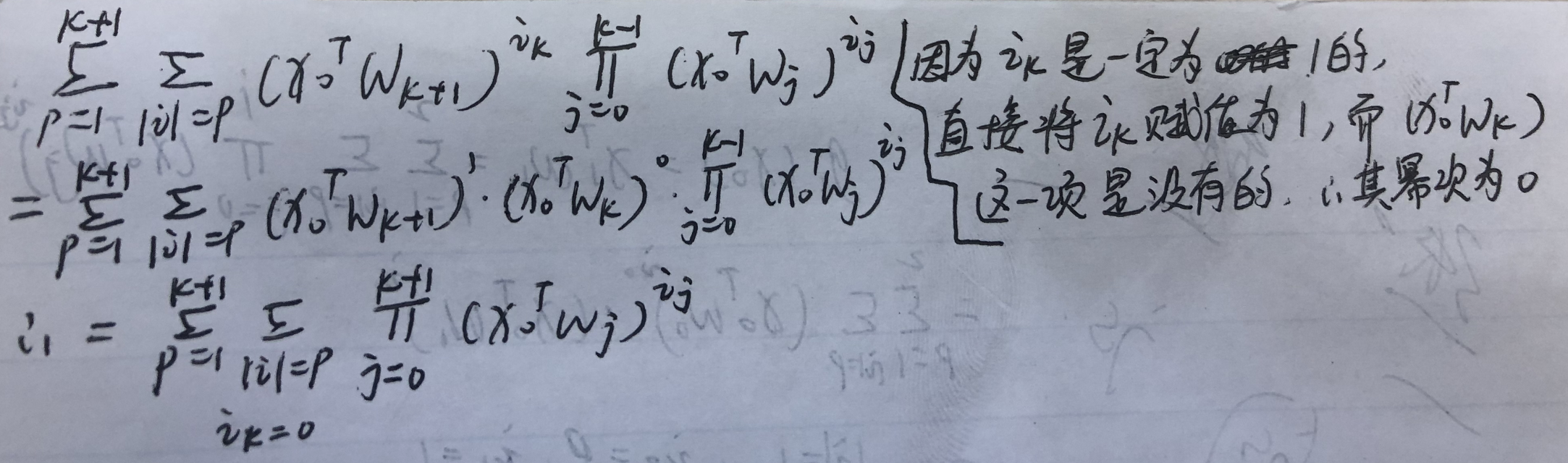
第二个等号转第三个等号就是左边项取出p=k+2，即第三个等号的第三项；右边项取出p=1，即第三个等号的第二项；然后左右项剩下的值即可合并得到第三个等号的第一项
）
第一个等式是将i的大小从k + 1增加到k + 2的结果。第二个等式使用的事实是，根据定义，i的最后一项总是1，最后一个等式也是如此。通过归纳假设，等式9在所有
都成立。接下来，我们通过重新安排等式9的项来计算
，即
的系数。注意，注意
的所有不同排列都是的形式。因此是等式9中与每个排列相关的所有权值的和。用于排序
的权重为：
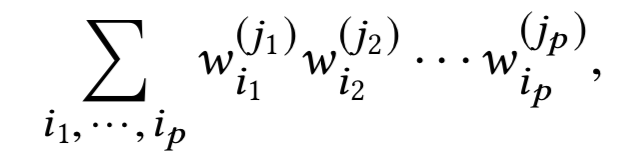
其中
属于所有用于
对应活跃指标的集合，具体来说就是：
因此，我们表示
为
的所有排列集合，然后得到想要的claim：
######
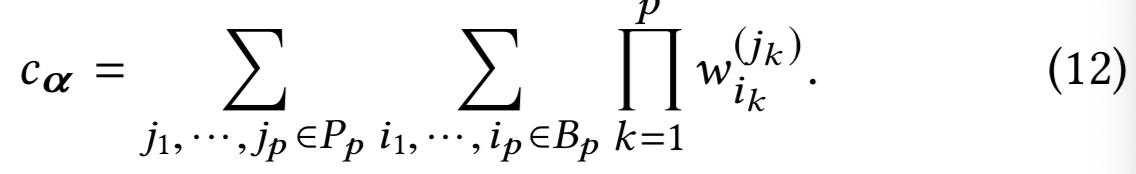
3.2 Generalization of FMs
cross网络模型继承了FM模型的参数共享精神，并将其进一步扩展到更深层次的结构中。
在FM模型中，特征xi与权重向量vi相关，交叉项xixj的权重由<vi,vj>计算。在DCN中，xi与标量
相关，交叉项xixj的权重是集合
和
参数的乘法。两个模型都使每个特征学习了一些独立于其他特征的参数，交叉项的权重是相应参数的某种组合
参数共享不仅提高了模型的效率，而且使模型能够对未知特征的交互进行泛化，对噪声具有更强的鲁棒性。例如，以具有稀疏特征的数据集为例。如果两个二进制特征xi和xj很少或从未在训练数据中共同出现，即
，则xixj的可学习的权重将不携带有意义的预测信息。
FM是一个窄的结构，限制了只表示degree为2的交叉项。相反，DCN可以构造所有的交叉项
，其degree 
以由层深度决定的某个常数为界，如定理3.1所述。因此，cross网络将参数共享的思想从单层扩展到多层且high-degree的交叉项。注意，与高阶FMs不同的是，cross网络中的参数数量只随输入维度数线性增长。
3.3 Efficient Projection
每个交叉层以高效的方式将x0和
之间的所有成对交互投射到输入的维度
比如
是一个交叉层的输入。首先交叉层隐式地构造了d2个成对交互
，然后以一种节省内存的方式隐式地将他们投射回d维度。然而，直接的方法会带来立方级成本
我们的cross层提供了一种高效的解决方案去减少损失到维度d的线性级。考虑
。其实际等价于：
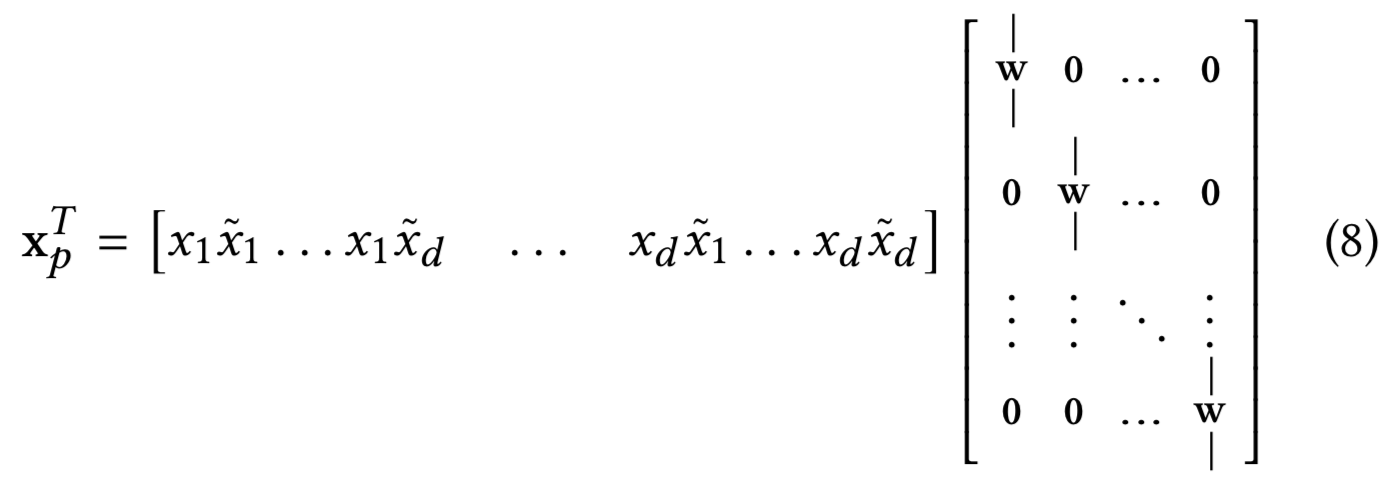
其中行向量包含d2个成对交互
，投影矩阵是一个块对角结构，
为列向量。
4 EXPERIMENTAL RESULTS
在本节中，我们评估DCN在一些流行的分类数据集上的性能。
4.1 Criteo Display Ads Data
Criteo Display Ads2数据集用于预测广告点击率。它有13个整数特征和26个类别特征，其中每个类别有一个高基数(cardinality，即每个类别有很多个种类)。对于这个数据集，logloss 0.001的改进都被认为是具有实际意义的。当考虑到庞大的用户群时，预测准确性的微小提高可能会导致公司收入的大幅增加。该数据包含7天内(约4100万条记录)的11GB大小的用户日志。我们使用前6天的数据进行训练，并将第7天的数据随机分割为相同大小的验证集和测试集。
4.2 Implementation Details
DCN是在TensorFlow上实现的，我们简要讨论了使用DCN进行训练的一些实现细节。
Data processing and embedding. 实值特征通过应用对数变换（log transform）进行归一化。对于类别特征，我们将特征嵌入到维数为 6×(category cardinality)1/4的稠密向量中。连接所有embeddings得到一个维度为1026的向量。
Optimization. 应用Adam优化器[9]进行mini-batch随机优化。batch大小设置为512。对深度网络应用Batch Normalization[6]，设置梯度clip范数为100。
Regularization. 我们使用early stopping，因为我们发现L2正则化和dropout是无效的。
Hyperparameters. 我们报告了基于网格搜索方法得到的不同隐藏层数、隐藏层大小、初始学习率和cross层数的结果。隐藏层的数量为2 ~ 5，隐藏层大小为32 ~ 1024。对于DCN，cross层数从1到6变化（更多的cross层并不会带来显著的改进，所以我们将其限制在一个小范围内进行微调）。初始学习率从0.0001调整到0.001，增量为0.0001（实验中，我们观察到对于Criteo数据集，大于0.001的学习率通常会降低性能。）。所有的实验都在训练第15万步时进行early stopping，因为超过这个阶段就开始发生过拟合。
4.3 Models for Comparisons
我们将DCN与5个模型进行了比较:无cross网络的DCN模型(DNN)、logistic回归(LR)、Factorization Machines (FMs)、Wide and Deep Model(W&D)和Deep Crossing(DC)。
DNN. embedding层、输出层和超参数调优过程与DCN相同。DCN模型的唯一变化是没有cross层。
LR. 我们使用了Sibyl[2]—一个用于分布式逻辑回归的大规模机器学习系统。整数特征在对数尺度上离散。交叉特征由一个复杂的特征选择工具选择。所有的单一特征都被使用了。
FM. 我们使用了一个具有所有细节的基于FM的模型。
W&D. 与DCN不同的是，它的wide组件以原始稀疏特征为输入，依靠穷举搜索和domain knowledge来选择预测交叉特征。我们跳过了比较，因为目前还没有选择交叉特征的好方法。
DC. 与DCN相比，DC不形成明显的交叉特征。它主要依靠stacking和残差单位来建立隐交叉。我们使用与DCN相同的embedding(stacking)层，然后使用另一个ReLu层生成残差单元序列的输入。残差单元数从1调到5，输入维数和交叉维数从100调到1026。
4.4 Model Performance
在本节中，我们首先列出了logloss中不同模型的最佳性能，然后对DCN和DNN进行了详细的比较，即进一步研究cross网络带来的影响。
Performance of different models. 表1列出了不同模型的最佳测试logloss。模型的最优超参数设置分别是有着2层大小为1024的deep层和有着6个cross层的DCN模型, 有着5层大小为1024的deep层的DNN, 有着输入为424维且cross维度为537的5个残差单元的DC,和有着42个cross特征的LR模型。cross网络结构越深，性能越好，说明cross网络的高阶特征交互是有价值的。我们可以看到，DCN的表现远远超过其他所有的模型。特别是，它的性能优于最先进的DNN模型，但只使用了DNN所消耗内存的40%。
对于每个模型的最优超参数设置，我们还报告了10次独立运行的测试logloss的平均值和标准差：
。可以看出，DCN的表现在很大程度上一直都优于其他模型。
Comparisons Between DCN and DNN. 考虑到cross网络只引入了O(d)个额外参数，我们将DCN与传统的深度网络进行了比较，给出了在不同内存预算和loss容忍度情况下的实验结果。
接下来，在所有的学习速率和模型结构中，一定数量的参数的损失被报告为最佳的验证损失。我们的计算中省略了embedding层的参数数量，因为这两个模型是相同的。
表2报告了实现所需logloss阈值所需的最小参数数量。从表2中我们可以看出，由于cross网络能够更有效地学习bounded-degree特征交互，DCN的内存效率几乎比单个DNN高出一个数量级。
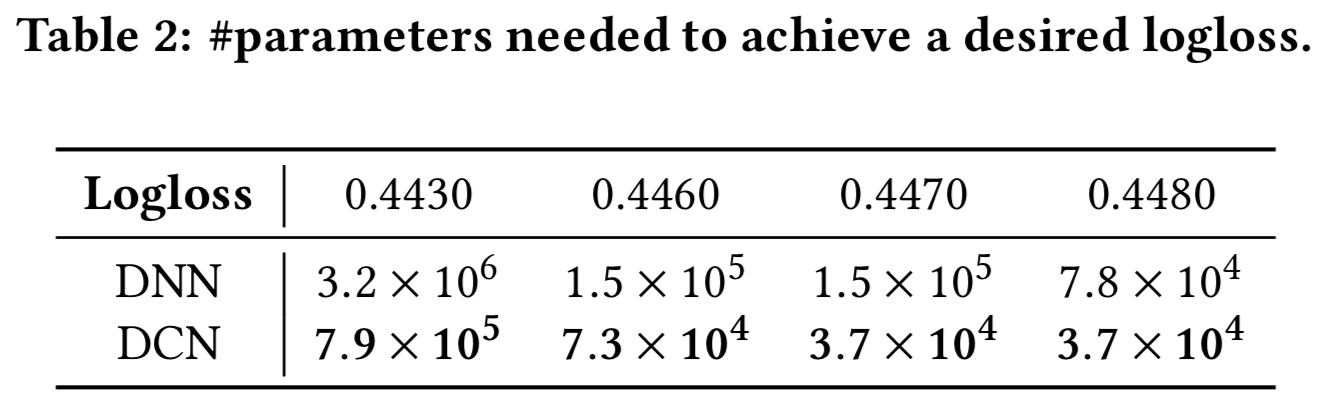
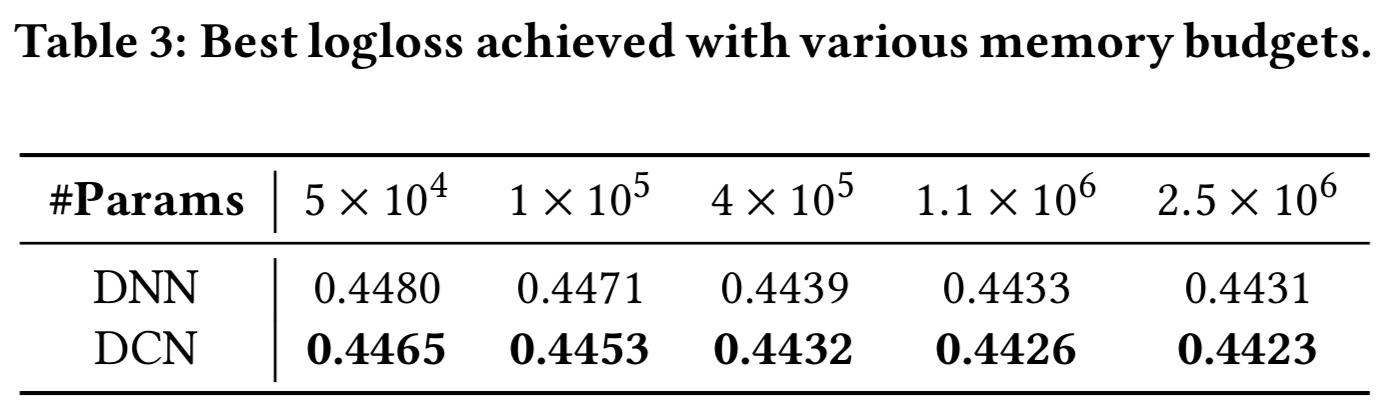
表3比较了受固定内存预算影响的神经模型的性能。我们可以看到，DCN的表现一直优于DNN。在小参数状态下，cross网络的参数数与深度网络的参数数相当，且明显的改善表明了cross网络在学习有效特征交互方面更加高效。在大参数范围内，DNN缩小了部分差距;然而，DCN的表现仍然远远优于DNN，这表明它可以有效地学习某些类型的有意义的特征交互，这是巨大的DNN模型也不能实现的效果。
我们通过说明在给定的DNN模型中引入交叉网络的效果来更详细地分析DCN。我们首先比较了相同层数和层大小下DNN和DCN的最佳性能，然后对每个设置，我们展示了随着更多的cross层的添加，验证logloss的变化。表4显示了DCN和DNN模型在logloss中的差异。在相同的实验设置下，DCN模型的最佳logloss始终优于同一结构的单一DNN模型。改进对所有超参数的一致性，缓解了初始化和随机优化带来的随机性影响。
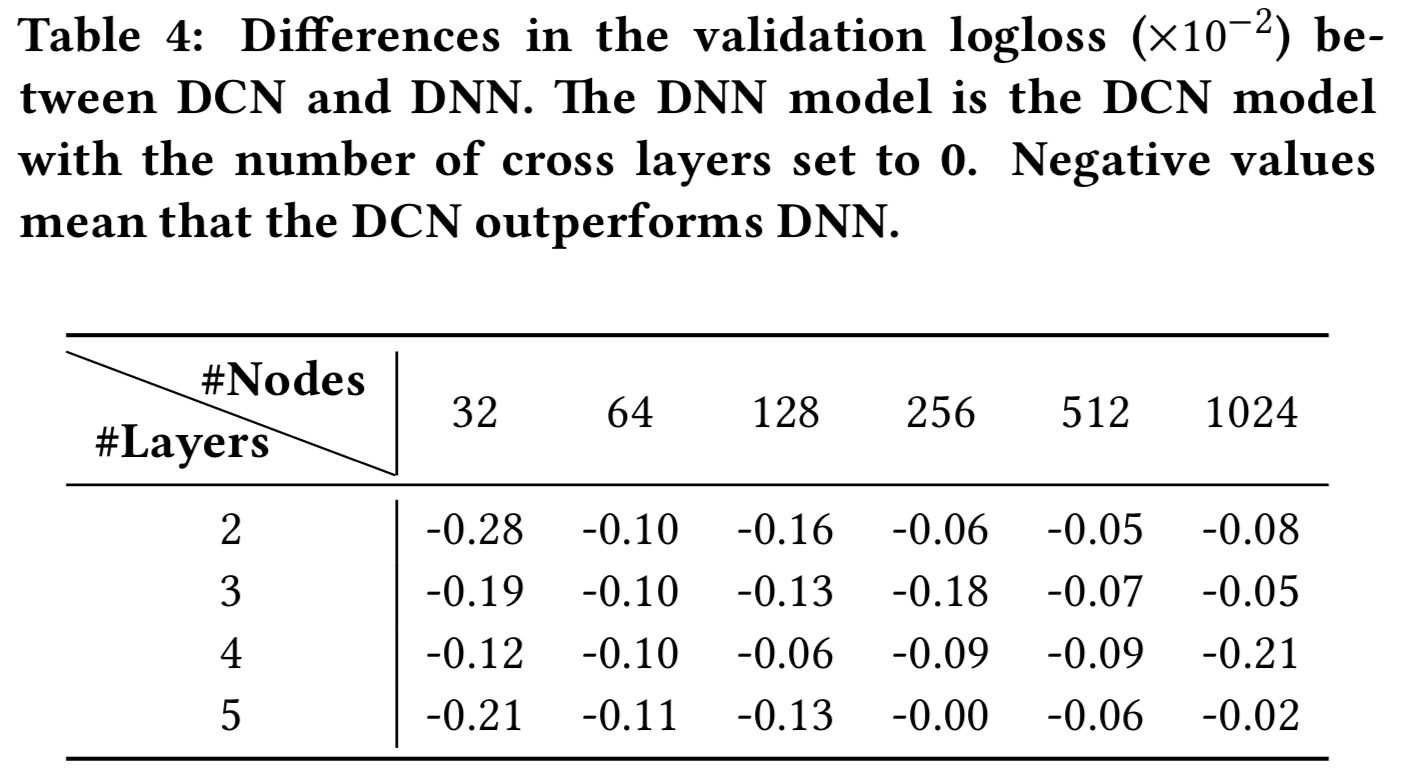
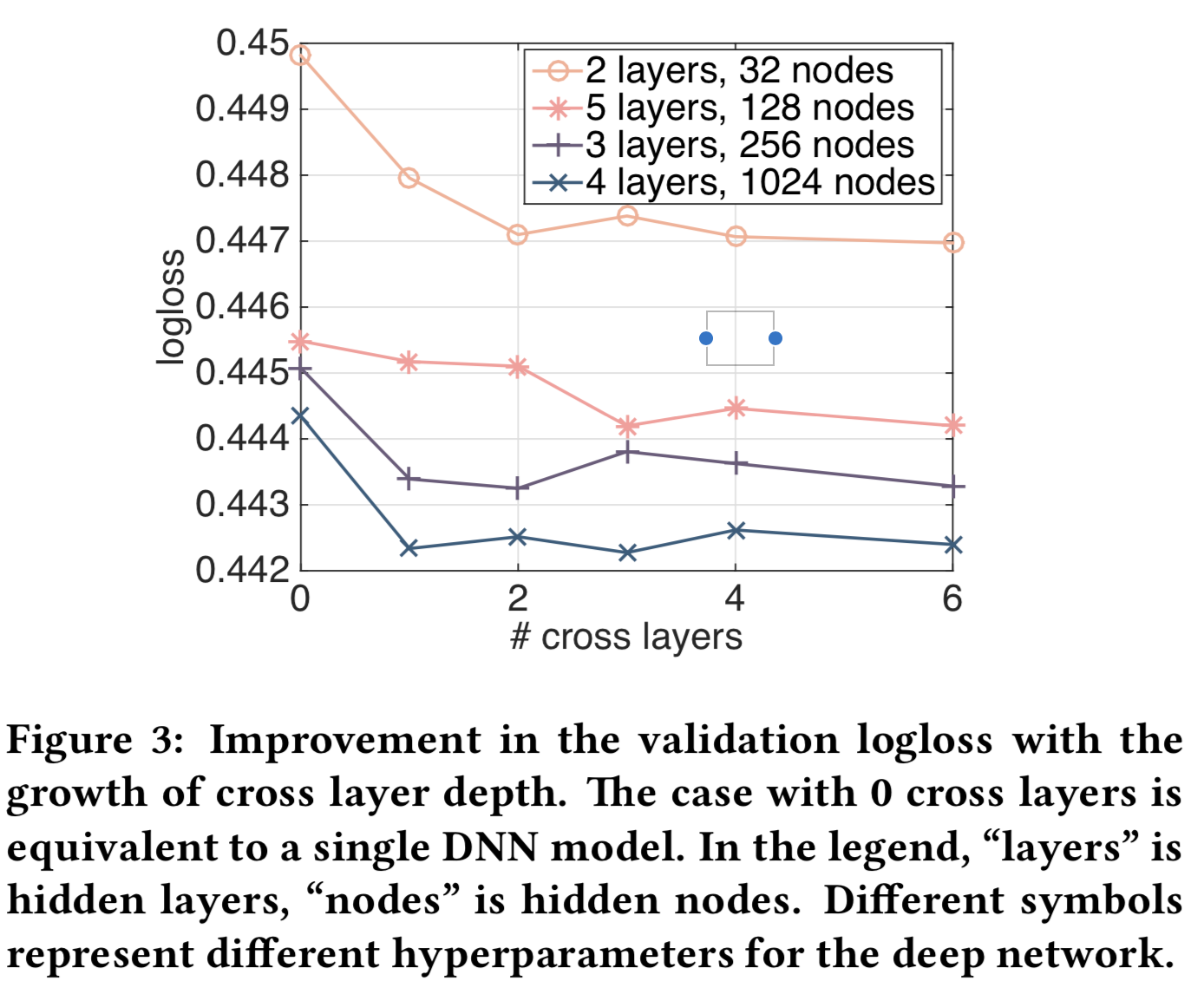
图3显示了在随机选择的设置中增加cross层的数量得到的改进效果。对于图3的深度网络，当1个cross层被添加到模型中时，得到了十分明显的改进。随着引入更多的cross层，对于某些设置，logloss继续减小，表明引入的cross项在预测中是有效的;而对于其他来说，logloss开始波动，甚至略有增加，这表明引入的high-degree特征交互没有帮助。
4.5 Non-CTR datasets
我们证明了DCN在非CTR预测问题上也表现良好。我们使用了来自UCI知识库的forest covertype(581012个样本和54个特征)和Higgs(11M样本和28个特征)数据集。将数据集随机分为训练集(90%)和测试集(10%)。对超参数进行了网格搜索。deep层层数范围为1 ~ 10层，层大小范围为50 ~ 300。cross层数范围为4 ~ 10层。残差单元的数量范围在1 ~ 5之间，输入维数和cross维数在50 ~ 300之间。对于DCN，输入向量直接输入到cross网络。
对于forest covertype数据，DCN的测试精度最高，为0.9740，内存消耗最少。DNN和DC均达到0.9737。每个模型的最优超参数设置为：DCN有着8个大小为54的cross层和6个大小为292的deep层，DNN有着7个大小为292的deep层，DC有着4个输入维数为271和cross维数287的残差单元。
对于Higgs数据，DCN的最佳测试logloss为0.4494,DNN为0.4506。DCN的最佳超参数设置为4个大小为28的cross层和4个大小为209的deep层，DNN为10个大小为196的deep层。DCN比DNN性能好，只使用了DNN的一半内存。
5 CONCLUSION AND FUTURE DIRECTIONS
识别有效的特征交互是许多预测模型成功的关键。遗憾的是，这个过程通常需要手工制作和穷举搜索。DNNs在自动特征学习中很受欢迎;然而，学习的特征是隐式且高度非线性的，网络在学习某些特征时可能会过大且低效。本文提出的深度cross网络可以处理大量稀疏和密集的特征集，并与传统的深度表征联合学习bounded degree的显式交叉特征。交叉特征的degree在每一cross层增加一级。我们的实验结果表明，在稀疏和密集数据集上，该算法在模型精度和内存使用方面都优于现有的算法。
我们希望进一步探索在其他模型中使用cross层作为构建块，实现对更深cross网络的有效训练，研究多项式近似下cross网络的效率，更好地理解优化过程中它与更深度网络的相互作用。
