What Deep CNNs Benefit from Global Covariance Pooling: An Optimization Perspective - 1 - 论文学习
What Deep CNNs Benefit from Global Covariance Pooling: An Optimization Perspective
Abstract
最近的研究表明,全局协方差池化(global covariance pooling, GCP)能够提高深度卷积神经网络(CNNs)在视觉分类任务中的性能。尽管取得了相当大的进展,但GCP对深层神经网络有效性的原因尚未得到很好的研究。在本文中,我们试图从优化的角度来理解深度CNN从GCP中得到的好处。具体来说,我们从优化损失的Lipschitzness和梯度的预测性两个方面探讨了GCP对深度CNN的影响,表明GCP可以使优化landscape更平滑,梯度更具有预测性。此外,我们还讨论了深度神经网络的GCP与二阶优化之间的联系。更重要的是,上述发现可以解释协方差池化方法训练深度CNN的几个优点,这些优点以前没有被识别或完全探索到,包括对网络收敛的显著加速(即,用GCP训练的网络可以支持学习率的快速衰减,在显著减少训练epochs的同时,取得了良好的性能),对图像损坏和扰动产生的失真实例具有较强的鲁棒性,对不同的视觉任务如目标检测和实例分割具有较好的泛化能力。我们在不同的任务上使用不同的深度CNN模型进行了广泛的实验,结果为我们的发现提供了有力的支持。
1. Introduction
全局协方差池化(Global covariance pooling, GCP)用于取代全局平均池(Global average pooling, GAP)来聚合深度卷积神经网络(deep convolutional neural networks, CNNs)的最后一个卷积激活,其在各种视觉任务中取得了显著的性能进步[20,30,12,41,11,26,29,25]。现有的基于GCP的研究主要集中于使用各种归一化方法[20,30,26,29]和更丰富的统计数据[41,9,8,3]来获得更好的性能,或者使用低维协方差表征来获得可比较的结果[13,22,14,42]。然而,GCP对深层神经网络有效的原因尚未得到很好的研究。虽然有一些研究从统计建模[20,30,26]或几何[26]的角度对其进行了解释,但GCP深度CNN的某些行为仍缺乏合理的解释。例如,如图1所示,为什么GCP可以显著加快深度CNN的收敛速度。特别是,采用GCP的网络可以达到与基于GAP的网络相匹配或更好的性能,但只使用了后者的不到1/4的训练epochs。
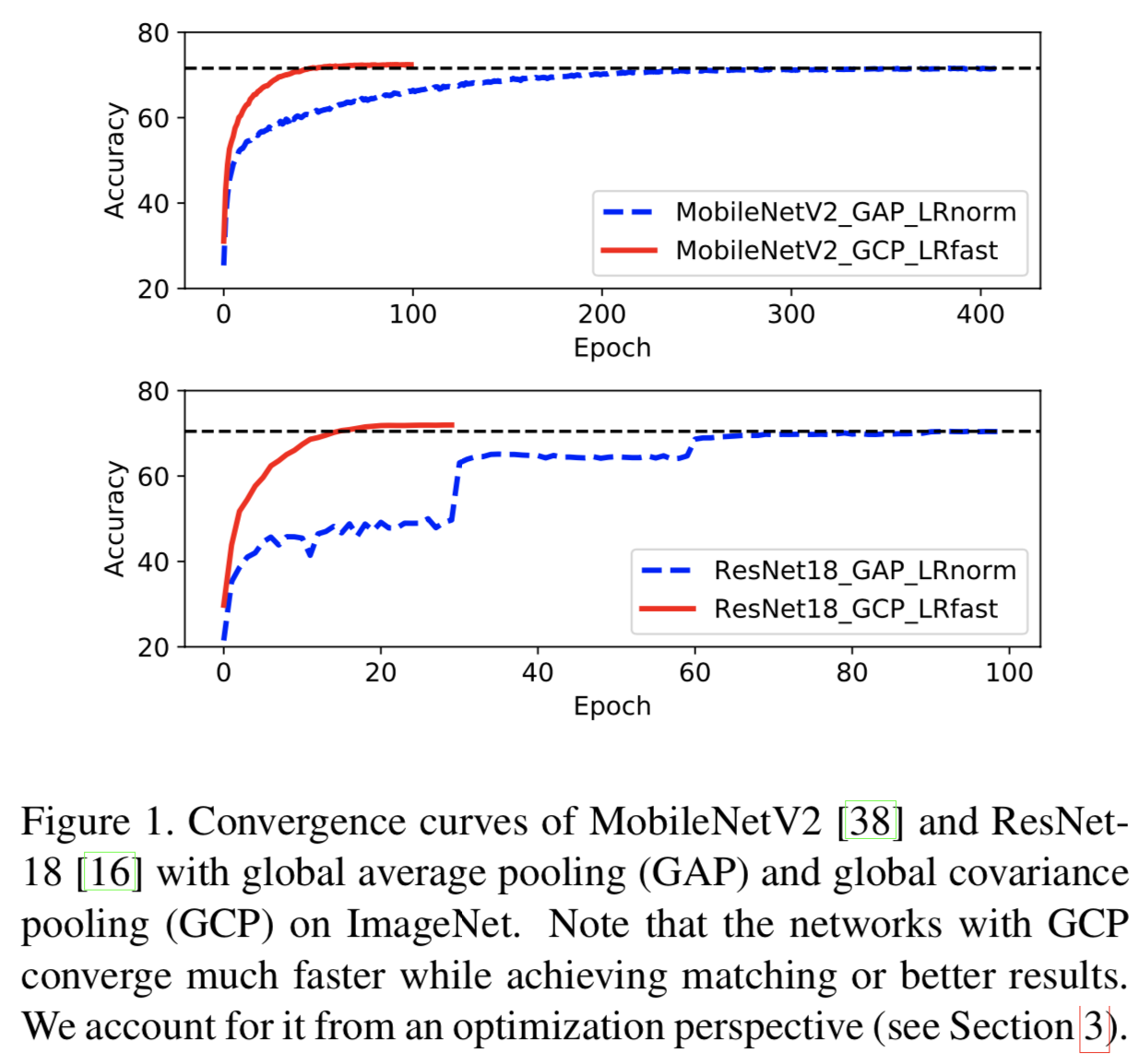
在本文中,我们试图从优化的角度理解GCP对深度CNN的有效性,从而直观地解释使用GCP的网络的行为。为此,我们受最近[39]工作的启发,探讨了GCP对优化landscape和深度CNN梯度计算的影响。具体来说,我们首先在大规模ImageNet[10]上训练两个广泛使用的CNN模型(即MobileNetV2[38]和ResNet-18[16]),分别使用GAP和GCP来聚合最后的卷积激活。然后,我们从优化的角度对它们进行比较,发现GCP可以提高优化损失的稳定性(即Lipschitzness)和梯度的稳定性(即预测性)。此外,在深度CNN背景下,通过分析GCP的反向传播和二阶优化[32,33,36],我们发现GCP对优化的影响与K-FAC[33,36]具有相似的理念。上面的发现提供了一个令人鼓舞的观点来理解深CNN中GCP的有效性,可以直观且合理地解释用GCP训练深度CNNs的行为,例如,GCP使优化landscape更光滑,导致网络收敛到一个更好的局部最小值(即,更好的性能可见[30,41,26]),并更快地收敛,如图1所示。
基于上述发现,我们可以解释用GCP训练深度CNNs时的几个优点,这些有点之前没有被识别或完全探索到。首先,由于GCP能够平滑优化landscape,使用GCP的深度CNN可以支持学习率的快速衰减以实现快速收敛。同时,之前的研究[39]表明,Lipschitzness的改善可以加速深度神经网络的收敛。为了验证这一点,我们在ImageNet[10]上使用各种深度CNN架构(即MobileNetV2 [38], ShuffleNet V2[31]和ResNets[16])进行实验。结果表明,在学习率快速衰减的条件下,使用GCP的深度神经网络在不到四分之一的训练epochs下达到了与使用GAP的深度神经网络相当的性能。通过调整学习率调度方法,采用GCP的深度神经网络可以使用更少的训练epochs收敛到更好的局部极小值。
其次,GCP提高了优化损失和梯度的稳定性,使深度神经网络对受某些畸变干扰的输入更鲁棒。与此同时,[7]的研究表明,对Lipschitz常数的控制有助于提高模糊分类器实例的鲁棒性。因此,我们在最近引入的IMAGENET-C和IMAGENET-P基准[17]上进行实验,其中失真是通过常见的图像损坏和扰动实现的。结果表明,GCP能显著提高深度神经网络对图像损坏和扰动的鲁棒性。
第三,GCP通常允许深度神经网络收敛到更好的局部最小值,从而利用GCP预处理的深度神经网络为其他视觉任务提供一个有效的初始化模型。因此,我们将预处理后的CNN模型转移到MS COCO基准[28]中进行目标检测和实例分割任务,结果表明,采用GCP预处理的CNN比基于GAP预处理的CNN更好。
本文的研究成果如下。(1)据我们所知,我们首次尝试从优化的角度理解GCP在深度CNN背景下的有效性。具体地,我们证明了GCP可以改善优化损失的Lipschitzness和梯度的预测性。此外,我们还讨论了GCP与二阶优化之间的联系。这些发现为更好地理解经GCP训练的深度CNNs的行为提供了一个令人激动的观点。(2)更重要的是,我们的上述发现可以解释GCP在训练深度CNNs上的一些优点,包括收敛速度的显著加快和学习率的快速衰减,对失真例子具有更强的鲁棒性,以及对不同视觉任务具有良好的泛化能力。(3)我们利用6个具有代表性的深度CNN架构对图像分类、目标检测和实例分割进行了广泛的实验,实验结果为我们的研究结果提供了有力的支持。
2. Related Work
DeepO2P[20]和B-CNN[30]是第一批将GCP引入深度CNNs的工作。DeepO2P将二阶(协方差)池化方法(O2P)[5]扩展到深度架构,而B-CNN通过可训练的双线性池化捕获局部卷积特征的交互。Wang等人[41]提出了一种全局高斯分布嵌入网络,联合利用了概率分布建模和深度学习的能力。Li等人提出了GCP的矩阵幂次归一化,并阐明了它的统计和几何机制。除了GCP之外,一些研究[8,3]提出使用更丰富的统计数据来进一步改进。上述方法从统计建模或黎曼几何的角度研究GCP。与之不同的是,我们从优化的角度解释了GCP的有效性,并进一步探讨了GCP在训练深度CNNs方面的优点。
由于深度CNNs本身就是黑盒,因此理解GCP对深度CNNs的影响仍然是一个具有挑战性的问题。最近的许多工作[43,44,39,2,45]致力于理解深度CNNs或分析基础成分的作用,如单个单元、批归一化(batch normalization, BN)[19]和优化算法。Zeiler等[43]和Zhou等人[45]分别通过最大激活单元的反褶积和图像区域来实现特征映射的可视化。Zhang等[44]和Bjorck等[2]设计了一系列对照实验,分别分析深度CNNs的泛化能力和理解BN对深度CNNs的影响。特别是,最近的一项工作[39]通过探索在CIFAR10[23]上训练的VGG-like网络[40]的优化landscape,研究了BN的影响,同时提供了使用全连接层的Lipschitzness改进的理论分析。在[39]的激励下,我们试图从优化的角度来理解GCP对深层CNNs的影响。
3. An Optimization Perspective for GCP
在本节中,我们首先回顾深度CNNs的全局协方差池化(GCP)。然后,我们分析了GCP对深度神经网络的平滑效果,最后讨论了它与二阶优化的关系。
3.1. Revisiting GCP
![]() 表示深度CNNs最后一个卷积层的输出,其中W、H和D分别表示特征的宽度、高度和维度。将
表示深度CNNs最后一个卷积层的输出,其中W、H和D分别表示特征的宽度、高度和维度。将![]() 作为最后预测的全局表征,大多数现有的CNNs使用了GAP,即
作为最后预测的全局表征,大多数现有的CNNs使用了GAP,即![]() ,其中特征特征标量
,其中特征特征标量![]() 被重置为一个特征矩阵
被重置为一个特征矩阵![]() ,其中
,其中![]() 。当前的很多研究[30,26]说明了GCP相对于GAP的优势。为了实现GCP,
。当前的很多研究[30,26]说明了GCP相对于GAP的优势。为了实现GCP,![]() 的样本协方差矩阵可以计算为:
的样本协方差矩阵可以计算为:
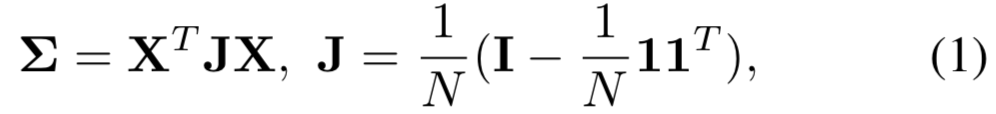
其中![]() 是N x N的单位矩阵,
是N x N的单位矩阵,![]() 是所有元素都为1的N维向量
是所有元素都为1的N维向量
归一化在GCP中有很重要的作用,不同的归一化方法都被研究了,包括matrix logarithm normalization [20], element-wise power normalization followed by l2 normalization [30], matrix square-root normalization [41, 29, 25] 和matrix power normalization [26]。其中,matrix square-root normalization(即幂次为1/2)倾向于在大规模和小规模视觉分类任务中考虑其的良好性能。因此,该论文使用带有matrix square-root normalization的GCP,即:
![]()
其中![]() 和
和![]() 分别表示特征向量矩阵和
分别表示特征向量矩阵和![]() 的特征值的对角矩阵
的特征值的对角矩阵
3.2. Smoothing Effect of GCP
为了了解GCP的作用机制,我们研究了GCP对深层神经网络优化landscape的影响。受[39]的启发,我们探讨了GCP对优化损失稳定性(即Lipschitzness)和梯度稳定性(即预测性)的影响。具体来说,为了检验优化损失的稳定性,我们在每个训练步骤中测量损失![]() 沿梯度方向的变化。给定输入
沿梯度方向的变化。给定输入![]() ,计算优化损失的变化为:
,计算优化损失的变化为:
![]()
其中![]() 表示损失关于输入
表示损失关于输入![]() 的梯度,其中
的梯度,其中![]() 是梯度下降的步长。很明显,
是梯度下降的步长。很明显,![]() 的变化(范围)越小,表示优化landscape更平滑,且在训练过程[39]中更容易控制。如[39]所示,等式(3)中
的变化(范围)越小,表示优化landscape更平滑,且在训练过程[39]中更容易控制。如[39]所示,等式(3)中![]() 的范围反映了优化损失的Lipschitzness
的范围反映了优化损失的Lipschitzness
为了检验梯度的稳定性,我们通过计算在一个步长区间上的原始梯度方向上的梯度和损失梯度之间的欧几里德距离来测量损失![]() 的梯度是如何变化的。因此,梯度预测可以表述为:
的梯度是如何变化的。因此,梯度预测可以表述为:
![]()
其中![]() 是步长。与优化损失的稳定性相似,
是步长。与优化损失的稳定性相似,![]() 变化范围越小,表示梯度对步长是不敏感的,即有着更好的梯度预测性。损失的Lipschitzness和梯度预测性极大地影响了深度神经网络的优化,即landscape的平滑性和对超参数的鲁棒性。
变化范围越小,表示梯度对步长是不敏感的,即有着更好的梯度预测性。损失的Lipschitzness和梯度预测性极大地影响了深度神经网络的优化,即landscape的平滑性和对超参数的鲁棒性。
根据以上讨论,我们分别用GCP和GAP对网络进行训练,并比较它们损失的Lipschitzness和梯度预测性来分析GCP的平滑效果。在不失去通用性的前提下,我们使用了广泛使用的MobileNetV2[38]和ResNet-18[16]作为backbone模型,并在大规模的ImageNet[10]上训练它们。为了使用GCP训练MobileNetV2和ResNet-18,遵循[26],将最后一次卷积激活的维数降至256,并使用与[38]和[16]具有相同超参数的随机梯度下降(SGD)训练网络。另外,我们没有使用dropout操作来避免MobileNetV2的随机性,且去掉了ResNet-18的conv5_x中的下采样操作
将![]() 和
和![]() 范围的左端点设为初始学习率,在保证GAP稳定训练的前提下,右端点尽量大。比如MobileNetV2和ResNet-18分别设置为
范围的左端点设为初始学习率,在保证GAP稳定训练的前提下,右端点尽量大。比如MobileNetV2和ResNet-18分别设置为![]()
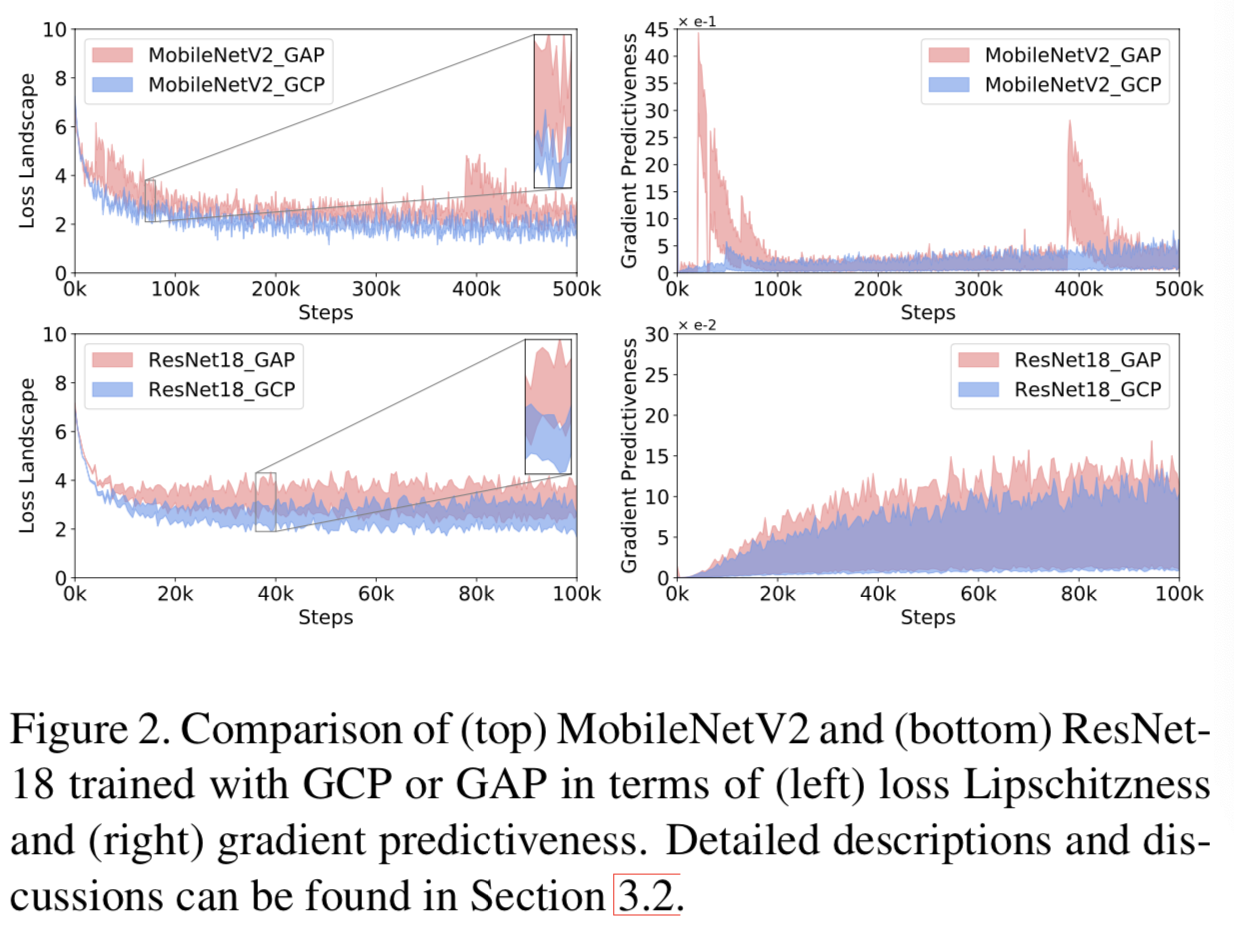
![]() 。使用GAP和GCP训练的500K steps(约37个epochs)的MobileNetV2和使用100K steps(约20个epochs)的ResNet-18在损失的Lipschitzness和梯度预测方面的行为分别显示在图2的顶部和底部。对于MobileNetV2和ResNet-18,我们观察到使用GCP的网络比基于GAP的网络的优化损失变化更小(即
。使用GAP和GCP训练的500K steps(约37个epochs)的MobileNetV2和使用100K steps(约20个epochs)的ResNet-18在损失的Lipschitzness和梯度预测方面的行为分别显示在图2的顶部和底部。对于MobileNetV2和ResNet-18,我们观察到使用GCP的网络比基于GAP的网络的优化损失变化更小(即![]() ),且使用GCP的网络的优化损失始终低于使用GAP训练的网络。这些结果表明,在相同的设置下,GCP可以改善优化损失的Lipschitzness,并且收敛速度更快。同时,对于梯度的变化,采用GCP的网络的
),且使用GCP的网络的优化损失始终低于使用GAP训练的网络。这些结果表明,在相同的设置下,GCP可以改善优化损失的Lipschitzness,并且收敛速度更快。同时,对于梯度的变化,采用GCP的网络的![]() 比基于GAP的网络更稳定,说明采用GCP的网络具有更好的梯度预测能力。此外,使用GAP的MobileNetV2在损失landscape和梯度预测的跳跃表明,损失和梯度的变化相当大,这表明不同的步长可能会导致损失不可控制地更高。相比之下,GCP的变化是相当小且一致的,这表明GCP有助于稳定的训练。总之,GCP具有平滑深度CNNs的优化landscape和提高梯度预测的能力。
比基于GAP的网络更稳定,说明采用GCP的网络具有更好的梯度预测能力。此外,使用GAP的MobileNetV2在损失landscape和梯度预测的跳跃表明,损失和梯度的变化相当大,这表明不同的步长可能会导致损失不可控制地更高。相比之下,GCP的变化是相当小且一致的,这表明GCP有助于稳定的训练。总之,GCP具有平滑深度CNNs的优化landscape和提高梯度预测的能力。
3.3. Connection to Second-order Optimization
此外,我们分析GCP的后向传播(BP)去探索其在深度CNNs优化中的影响。让![]() 表示最后卷积层的输出,对于GAP层,损失
表示最后卷积层的输出,对于GAP层,损失![]() 关于的
关于的![]() 的梯度可计算为
的梯度可计算为![]()
![]() ,其中
,其中![]() 是一个常量矩阵。为了更新最后卷积层的权重
是一个常量矩阵。为了更新最后卷积层的权重![]() ,梯度下降如下实现:
,梯度下降如下实现:
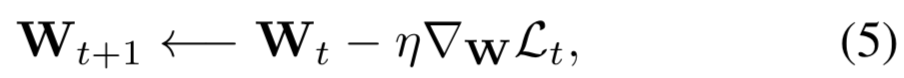
其中![]() ,t表示第t次迭代。
,t表示第t次迭代。
让![]() 。对于GCP层,损失关于
。对于GCP层,损失关于![]() 的导数可以写成:
的导数可以写成:
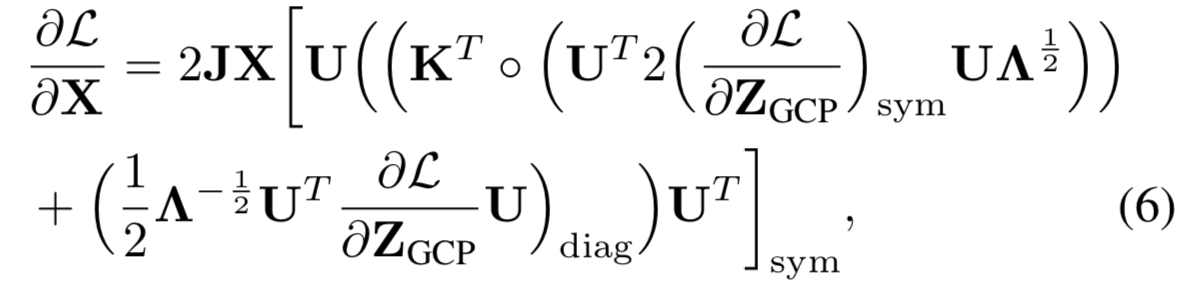
其中,![]() 和
和![]() 分别为特征向量矩阵和
分别为特征向量矩阵和![]() 样本协方差特征值的对角矩阵,
样本协方差特征值的对角矩阵,![]() 为与特征值相关的mask矩阵。在这里,
为与特征值相关的mask矩阵。在这里,![]() 表示矩阵Hadamard 乘积;(·)sym和(·)diag分别表示矩阵对称化和对角化。更多细节可参考[21,41,26]。通过一些假设和简化,等式(6)可修剪为:
表示矩阵Hadamard 乘积;(·)sym和(·)diag分别表示矩阵对称化和对角化。更多细节可参考[21,41,26]。通过一些假设和简化,等式(6)可修剪为:
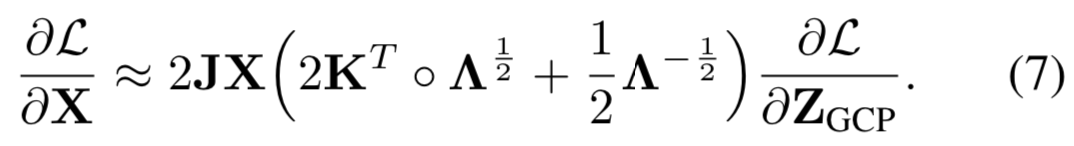
等式(6)和等式(7)的细节可见补充文档。将等式(7)替换到等式(5)中,我们可以大致更新卷积权重为:
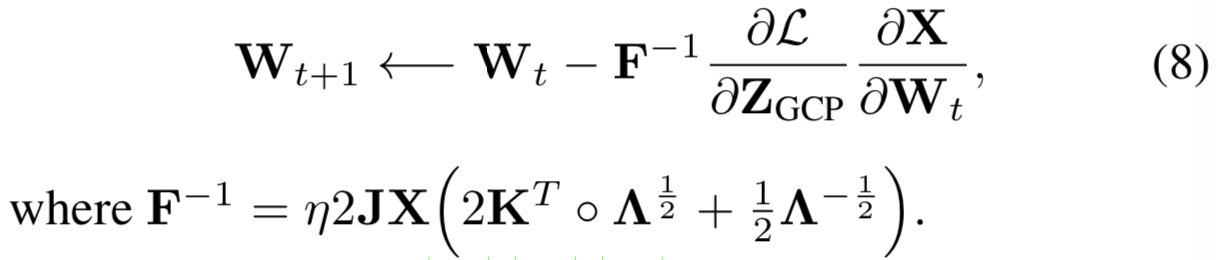
之前的工作[32,33,36]说明了二阶优化(即![]() )能加快深度神经网络的训练。可是Hessian矩阵(
)能加快深度神经网络的训练。可是Hessian矩阵(![]() )的求反计算是十分昂贵的,且对噪音敏感。因此,很多方法[32,33,1]被提出去近似
)的求反计算是十分昂贵的,且对噪音敏感。因此,很多方法[32,33,1]被提出去近似![]() 。最近,基于Fisher information矩阵的精确近似的K-FAC[33,36]被证明在优化深度CNNs中是有效的,其使用卷积层输入的取反值(即
。最近,基于Fisher information矩阵的精确近似的K-FAC[33,36]被证明在优化深度CNNs中是有效的,其使用卷积层输入的取反值(即![]() )和损失关于输出的梯度的取反值(即
)和损失关于输出的梯度的取反值(即![]() )之间的Kronecker内积来近似
)之间的Kronecker内积来近似![]() 。GAP、GCP和带有GAP的K-FAC的梯度在表1中进行对比,其中GCP修剪后的BP(等式7)与K-FAC共享相似的理论。主要的不同在于
。GAP、GCP和带有GAP的K-FAC的梯度在表1中进行对比,其中GCP修剪后的BP(等式7)与K-FAC共享相似的理论。主要的不同在于![]() 是由输出
是由输出![]() 和其特征值计算得到的,而
和其特征值计算得到的,而![]() 是由输入
是由输入![]() 和梯度
和梯度![]() 近似得到的。在4.1节的实验说明了使用GCP的ResNet-50使用更少的训练epochs就能得到和K-FAC[36]相匹配的结果,这可能表明GCP的BP可作为Hessian矩阵的pre-conditione的潜在替代品。
近似得到的。在4.1节的实验说明了使用GCP的ResNet-50使用更少的训练epochs就能得到和K-FAC[36]相匹配的结果,这可能表明GCP的BP可作为Hessian矩阵的pre-conditione的潜在替代品。

4. Merits Benefited from GCP
在前一节中,我们从优化的角度探讨了GCP对深度CNNs的影响。具体地,我们展示了GCP对优化landscape的平滑效应,并讨论了GCP与二阶优化之间的联系。此外,这些发现也可以解释GCP在训练深度CNNs方面的一些优点,这些优点以前没有被识别或完全探索过,包括网络收敛的显著加速、对由图像损坏和扰动产生的失真实例具有更强的鲁棒性和对不同视觉任务具有较好的泛化能力。在本工作中,所有程序均采用Pytorch软件包(https://github.com/ZhangLi- CS/GCP_Optimization)实现,并在具有4个NVIDIA RTX 2080 Ti GPUs的工作站上运行。具体描述如下。
4.1. Acceleration of Network Convergence
众所周知,深度CNNs的训练是一个耗时的过程,需要大量的计算资源。因此,加速网络收敛对于深度神经网络的快速训练起着关键作用,特别是对于大规模训练数据集来说。以往的研究[25]表明,经过GCP训练的网络比基于GAP训练的网络收敛更快,这可以用我们的研究结果来解释。其中,Lipschitzness改进[39,35]和GCP带来的二阶优化[36]的连接可以加速网络的收敛。在这里,我们进一步表明,由于具有平滑优化landscape的能力,采用GCP的深度CNNs可以支持学习率的快速衰减,从而显著提高收敛速度。为了验证这一点,我们在ImageNet上使用6个代表性的深度CNN架构进行了广泛的实验,包括MobileNetV2[38]、ShuffleNet V2[31]和18、34、50和101层的ResNets[16]。
具体来说,我们通过改变学习率(lr)的设置来训练所有使用GAP和GCP的网络。首先,我们使用每篇原始论文中的lr的设置,用LRnorm来表示。如[36]所示,使用二阶优化(K-FAC)的ResNet-50收敛速度更快,其中lr由多项式衰减调度,即:

其中![]() 是初始的lr;e、es和ef分别表示第e、开始和最后的epochs。受[36]的启发,我们在等式(9)中使用了lr的设置以实现ResNets的快速训练。为了决定参数
是初始的lr;e、es和ef分别表示第e、开始和最后的epochs。受[36]的启发,我们在等式(9)中使用了lr的设置以实现ResNets的快速训练。为了决定参数![]() ,我们设置
,我们设置![]() 为0.1,且在ImageNet中使用不同的
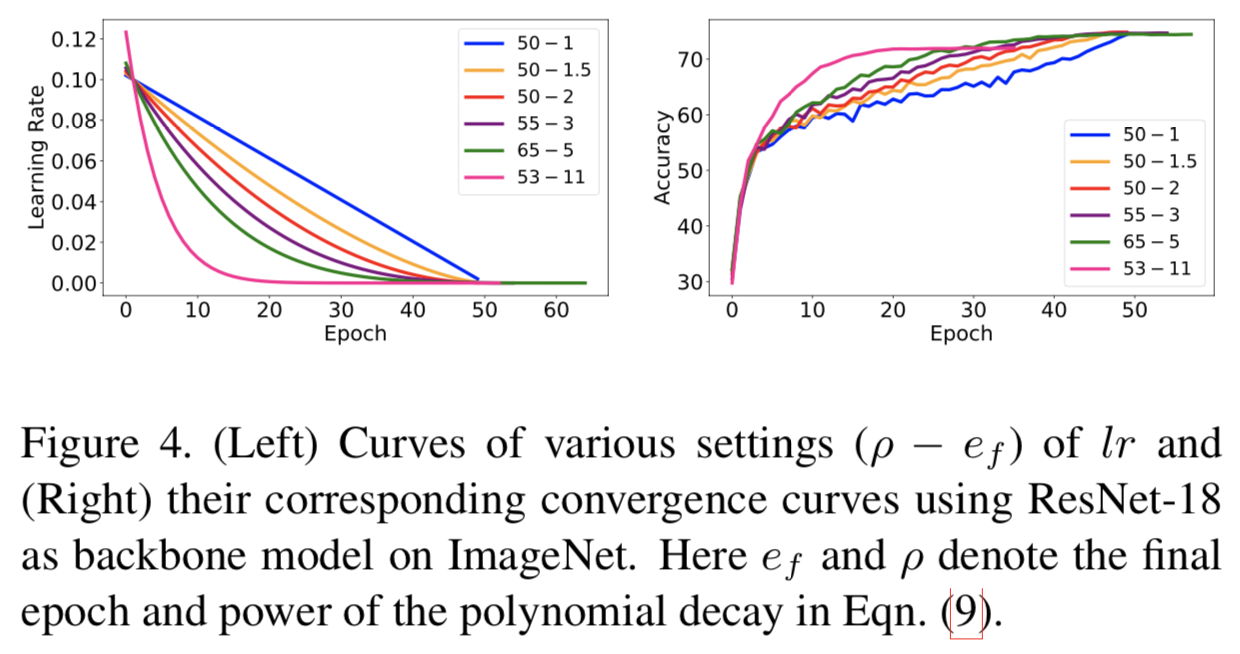
为0.1,且在ImageNet中使用不同的![]() 去训练带有GCP的ResNet-18,同时控制ef小于65,这些设置与[36]一致。图4说明了每个lr和其关联收敛的曲线。很明显,越大的
去训练带有GCP的ResNet-18,同时控制ef小于65,这些设置与[36]一致。图4说明了每个lr和其关联收敛的曲线。很明显,越大的![]() 能得到越快的收敛,但是会得到更低的准确度。(
能得到越快的收敛,但是会得到更低的准确度。(![]() =11,ef=53)的设置有最快的收敛,后面将其表示为LRfast,其在30个epochs中收敛。其中,(
=11,ef=53)的设置有最快的收敛,后面将其表示为LRfast,其在30个epochs中收敛。其中,(![]() =2,ef=50)在收敛速度和分类准确度中得到的最好的平衡,表示为LRadju。
=2,ef=50)在收敛速度和分类准确度中得到的最好的平衡,表示为LRadju。
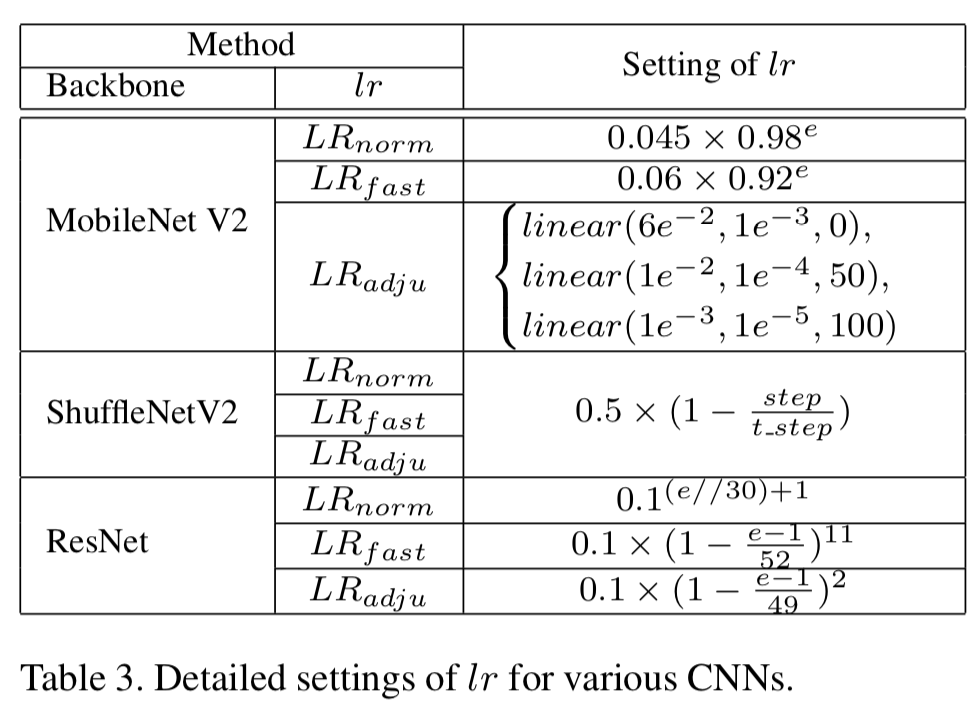
对于MobileNetV2,原始lr使用指数衰减方法(即0.045 x 0.98e)来调节,我们通过降低基数且提高初始lr来设置LRfast,即得到0.06 x 0.92e。LRadju使用stage-wise线性衰减方法来调节,即在第e个epoch调节为![]() ,其中
,其中![]() 分别表示每个stage的初始lr、最终lr和开始epoch。ShuffleNetV2的lr在原始论文中使用step-wise线性衰减方法来调节,总steps数量(即t_step)为3e5(~240 epochs)。对于ShuffleNetV2,LRfast和LRadju分别将训练epochs减少为60和100。lr设置的细节总结在表3中。
分别表示每个stage的初始lr、最终lr和开始epoch。ShuffleNetV2的lr在原始论文中使用step-wise线性衰减方法来调节,总steps数量(即t_step)为3e5(~240 epochs)。对于ShuffleNetV2,LRfast和LRadju分别将训练epochs减少为60和100。lr设置的细节总结在表3中。
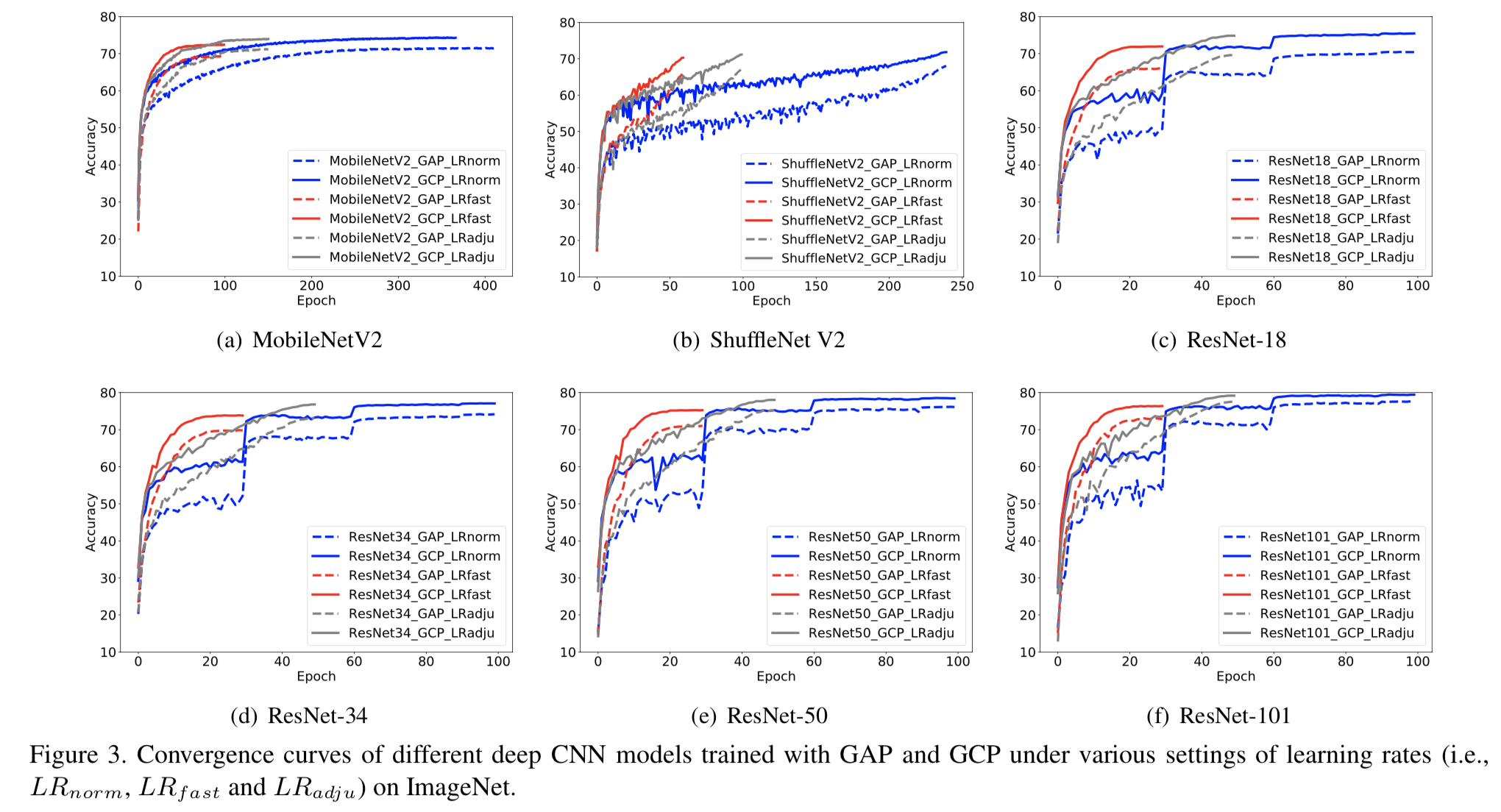
用GAP和GCP训练的不同网络在不同lr设置下的收敛曲线如图3所示,从中我们可以得到以下观察结果。(1)与LRnorm条件下训练的网络相比,在LRfast和LRadju条件下训练的网络性能有所下降。然而,与基于GAP的网络相比,GCP网络的性能退化程度要小一些,特别是在LRfast下。(2)使用LRfast训练的GCP网络下仅需要使用在LRnorm条件下训练GAP网络1/4的epoch数就能获得更好或匹配的结果。
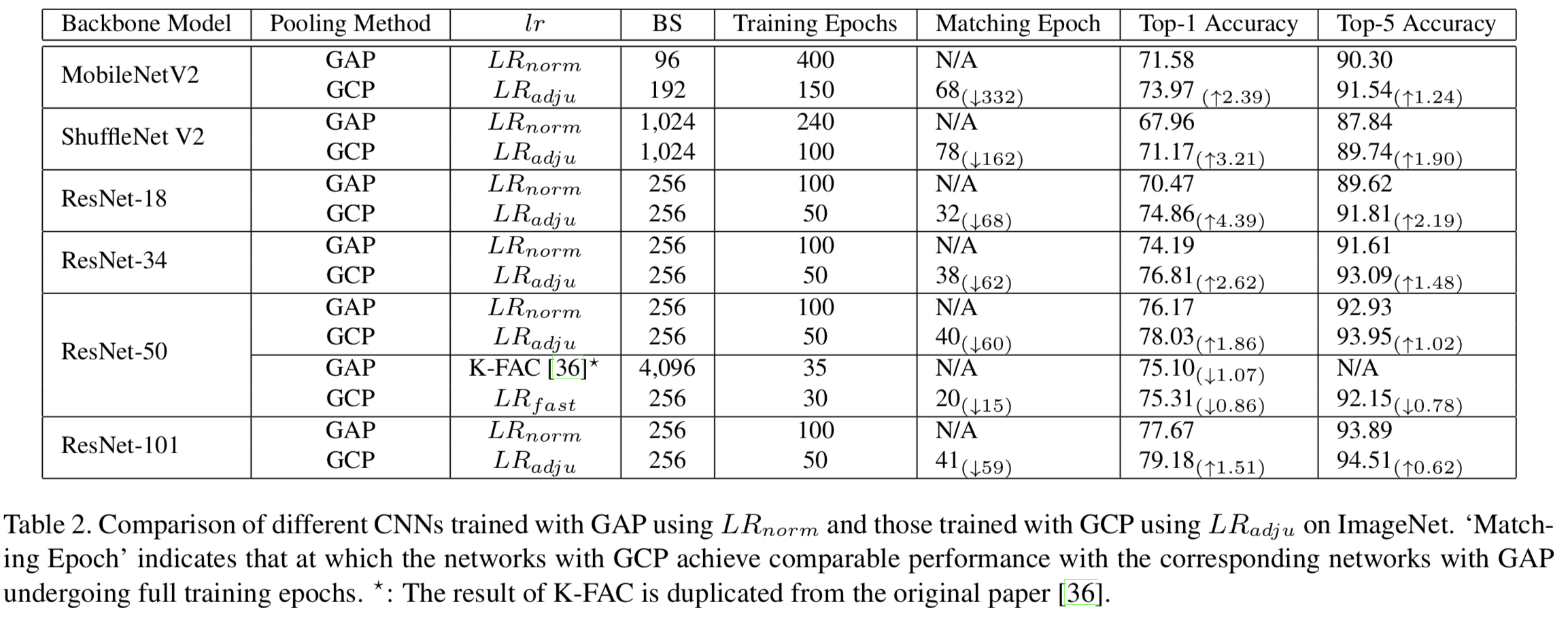
此外,我们还比较了在LRnorm(即原始设置)下使用GAP训练的网络和使用LRadju的GCP训练的网络。根据表2的结果,我们总结如下。(1)与LRnorm下GAP训练的网络相比,LRadju下GCP训练的网络在使用更少训练epochs的情况下获得更高的准确率。(2)采用GCP的网络使用更少的训练epochs就可以获得与基于GAP的网络相匹配或相当的准确度,特别是对于轻量级CNN模型,即MobileNetV2和ShuffleNet V2。例如,带有GCP的MobileNetV2 只使用68个epochs就实现了与基于GAP的网络相匹配的准确度,而后者需要大约400个epochs。(3)与二阶优化方法K-FAC[36]相比,GCP方法使用较少的训练epochs获得稳健的准确度增益,且仅使用20个epochs就得到和K-FAC方法相当的准确度。此外,GCP更容易实现。以上大量实验有力地支持了我们的发现:GCP使用学习率的快速衰减可以显著加快深度CNNs的收敛速度。
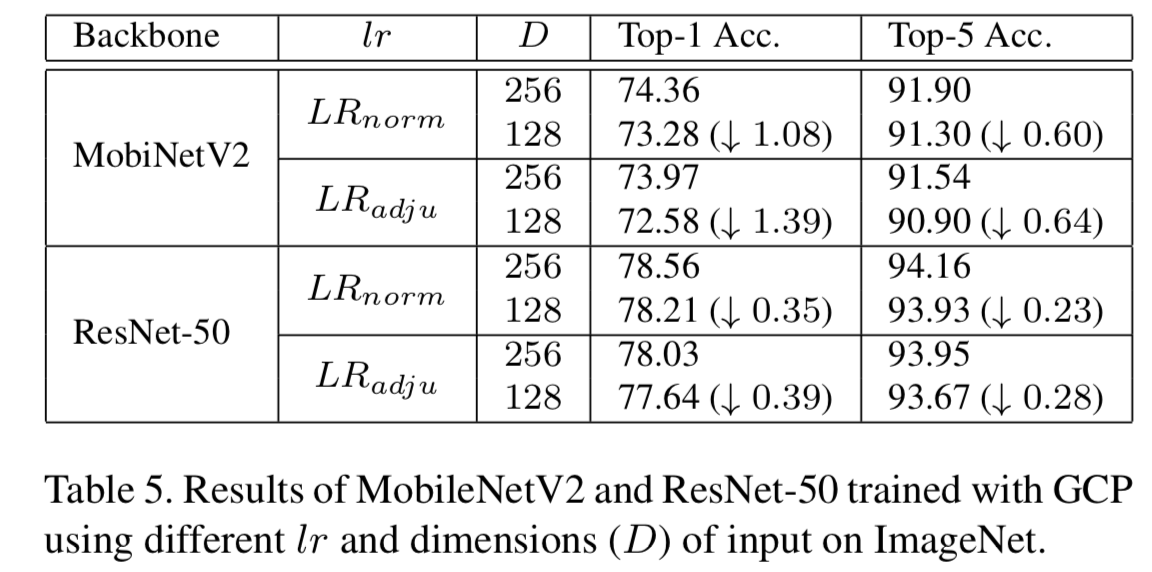
此外,我们在ImageNet上使用MobileNetV2 (MobiNetV2)和ResNet-50评估协方差表征维度(COV-Reps)对收敛行为的影响。如果输入特征的维数为D, GCP将输出一个D(D + 1)/2 维的COV-Reps。这里,我们将D设置为256(默认设置)和128,分别在LRnorm和LRadju的设置下训练网络。结果如表5所示,从表中可以看出,低维COV-Reps仍然允许深度CNNs更快地收敛,但收敛速度越快(即LRadju),性能下降越大。这表明COV-Reps的维数对收敛行为有重要影响。因此,如何在保留高维COV-Reps优点的同时压缩COV-Reps是一个重要的问题。尽管有很多关于COV-Reps压缩的研究被提出[13,22,42],但它们仍未在大规模场景下得到验证。基于知识精馏[18],从高维COV-Reps中学习紧凑的COV-Reps是一种可能的解决方案,我们将在未来的研究中进一步研究。
4.2. Robustness to Distorted Examples
GCP对损失的Lipschitzness和梯度预测性的改善,使网络对受畸变干扰的输入更加具有鲁棒性。我们还注意到[7]中陈述了类似的结论。为了验证这一点,我们对最近引入的IMAGENET-C和IMAGENET-P基准[17]进行了实验。与研究了 作为用于网络鲁棒性分析的一种最坏情况 的对抗扭曲(adversarial distortions)的影响的文献[4,34]不同,这两个基准设计用于评估深度CNNs对常见图像损坏和扰动的鲁棒性,它与对抗扭曲有关,在safety-critical应用中起着关键作用。
IMAGENET-C基准在ImageNet的验证集上执行50种类型的损坏(例如,噪声、模糊、天气和数字),每种损坏有5个级别的严重程度。IMAGENET-P 基准通过执行十多种扰动,如运动和缩放模糊、亮度、平移、旋转、缩放和倾斜扰动,在ImageNet的验证集上生成一系列扰动序列。我们按照[17]中的标准协议,在ImageNet的训练集(干净图像)上对所有CNN模型进行训练,并在IMAGENET-C和IMAGENET-P 基准上报告结果。评估指标包括IMAGENET-C的mean Corruption Error (mCE)和 Relative mean Corruption Errors (Relative mCE), IMAGENET-P的mean Flip Rate (mFR) 和 mean Top-5 Distance (mT5D) 。关于指标的详细信息可以参考[17]。请注意,值越低,所有评估指标的性能就越好。
为了比较的公平,我们采用了作者发布的评估代码。注意,AlexNet[24]是一个基线模型,它在所有评估指标上都获得了100的值。采用GAP和GCP的不同深度CNNs的结果如表4所示,我们可以看出,采用GCP的网络显著优于基于GAP的网络,说明GCP可以大大提高深度CNNs对常见图像破坏和扰动的鲁棒性。值得注意的是,使用BN的VGG-VD19[40]和VGG-VD19在指标mCE、Relative mCE、mFR、mT5D上分别达到88.9、122.9、66.9、78.6和81.6、111.1、65.1、80.5的效果 。BN虽然改善了Lipschitzness,但它对扰动并不鲁棒。相比之下,GCP对于损坏和扰动都是鲁棒的。在[17]中,许多方案被提出来提高对损坏和扰动的鲁棒性,我们的工作表明GCP是一种新颖的和有前途的解决方案。此外,将GCP方案与其他方案相结合有进一步改进的潜力。

4.3. Generalization Ability to Other Tasks
由于GCP通常允许深度神经网络收敛到更好的局部最小值,在大规模数据集上预训练带有GCP的网络可以为其他视觉任务提供更好的初始化模型。也就是说,他们可能具有很好的泛化能力。为了验证这一点,我们首先在ImageNet上训练带有GCP的网络,然后直接应用于目标检测和实例分割任务。具体来说,我们使用ResNet-50和ResNet-101作为backbone模型,在MS COCO[28]上使用Faster R-CNN[37]和Mask R-CNN[15]作为基本检测器,比较了训练的带有GAP和GCP的网络的性能。对于使用GCP的训练网络,Li等人[26]建议在conv5_1中不进行降采样。但这增加了最后一个特征图的分辨率,同时导致更大的计算成本,特别是在需要大尺寸输入图像的目标检测和实例分割时。为了解决这一问题,我们引入了两种策略:(1)我们仍然使用原ResNet中的下采样方法,该方法由GCPD表示;(2)在conv5_1前插入一个步长为2的最大池化层进行下采样,表示为GCPM。
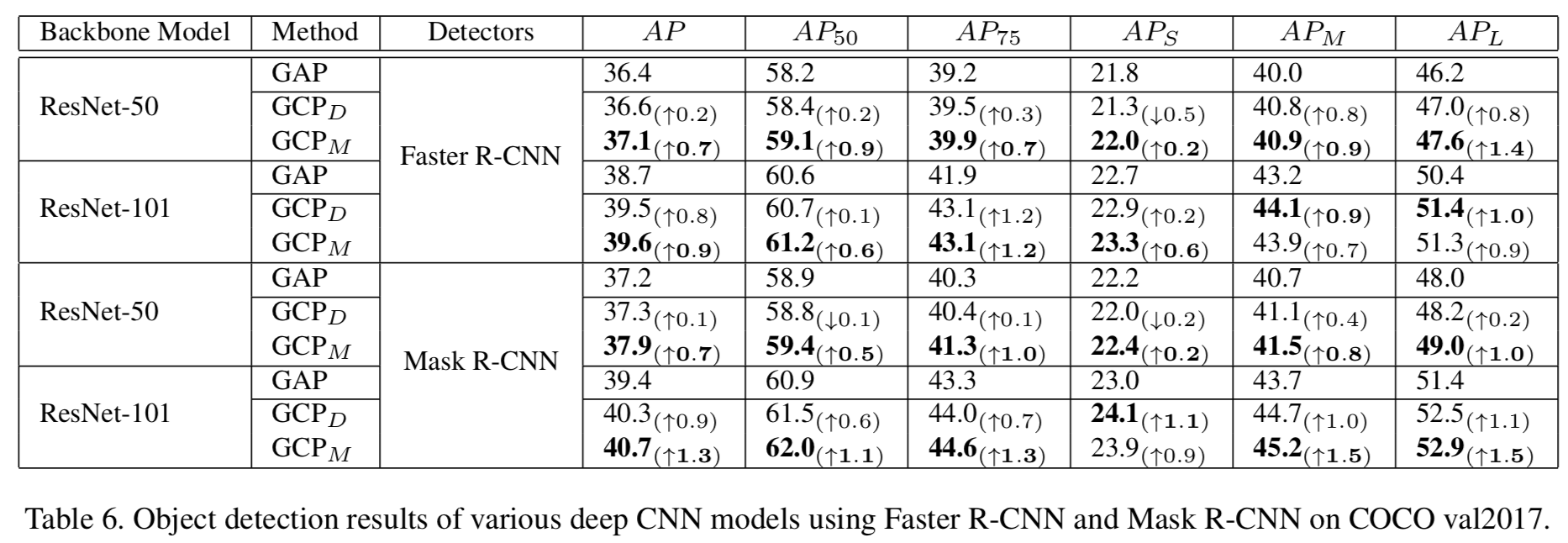
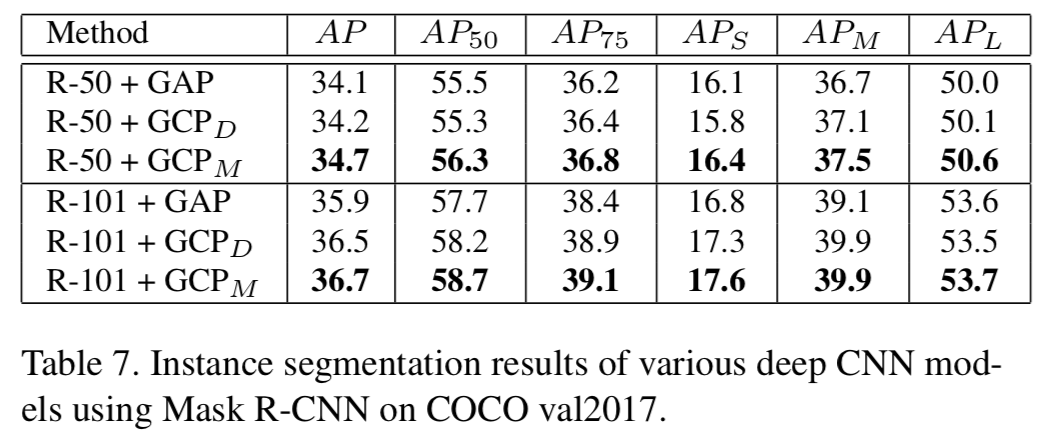
为了进行公平的比较,所有的方法都由MMDetection工具包[6]实现,设置相同(默认)。具体来说,输入图像的短边被调整为800,使用SGD来优化网络,其权重衰减为1e-4,动量为0.9,mini-batch大小为8。在COCO的train2017上,所有检测器都在12 epoch内训练,学习率初始化为0.01,在第8和11 epoch后分别将学习率降低10倍。报告了val2017的结果以作比较。如表6所示,GCPM优于GCPD,两者都优于GAP。具体来说,对于ResNet-50, 使用Faster R-CNN和Mask R-CNN作为检测器的GCPM在AP方面比GAP提高了0.7%。对于ResNet-101, GCPM在Faster R-CNN和Mask R-CNN上的表现分别比GAP高出0.9%和1.3%。对于表7中的实例分割结果,GCPM使用ResNet-50 (R-50)和ResNet-101 (R-101)作为backbone模型,分别将GAP提高了0.6%和0.8%。值得注意的是,当backbone模型和检测器更强时,GCP带来更多的改进。这些结果表明,采用GCP预处理的网络能够很好地推广到不同的视觉任务,表明采用GCP的网络能够提供更好的初始化模型。
如前所述,将GCP集成到ResNets中,抛弃了conv5_1中的下采样(DS)操作,以获得更多的采样特征,从而获得更有前景的分类性能。但是,它降低了conv5_x的分辨率,增加了计算成本,特别是对于大尺寸的输入图像来说。在这里,我们评估了它对GCP性能的影响。具体来说,我们使用ResNet-18、ResNet-50和ResNet-101作为backbone模型,并比较了使用或不使用DS的GCP的结果(即conv5_1的步数为2)。对于目标检测,我们使用Faster R-CNN作为基本检测器。如表8所示,对于每个模型的ImageNet分类,采用DS的GCP都不如不采用DS的GCP;但采用DS的GCP在目标检测方面表现更好。这些结果表明,对于GCP训练的网络,引入DS可以平衡分类精度、目标检测性能和模型复杂度。

5. Conclusion
在本文中,我们尝试从优化的角度分析GCP对深度神经网络的有效性。具体来说,我们证明了GCP能够改善深度神经网络损失的Lipschitzness和梯度预测性,并讨论了GCP与二阶优化之间的联系。我们的研究结果可以解释之前GCP在训练深度CNNs时未被识别或完全探索到的一些优点,包括网络收敛的显著加速、对扭曲实例更强的鲁棒性以及对不同视觉任务良好的泛化能力。广泛的实验结果为我们的发现提供了有力的支持。我们的研究为理解GCP提供了一个鼓舞人心的视角,有助于研究者在深度CNNs上下文中探索GCP的更多优点。在未来,我们将研究GCP平滑效果的理论证明以及它与二阶优化的严格联系。



