人脸识别（不确定性）- Probabilistic Face Embeddings - 1 - 论文学习

 

https://github.com/seasonSH/Probabilistic-Face-Embeddings

Probabilistic Face Embeddings

Abstract

嵌入(embedding)方法通过在潜在语义空间中比较人脸特征，取得了成功的人脸识别。然而，在完全不受约束的人脸设置中，通过嵌入模型学习到的人脸特征可能是模糊的，甚至可能不存在于输入人脸中，导致噪声表征。我们提出了Probabilistic Face Embeddings (PFEs)，它在潜在空间中以高斯分布表示每个人脸图像。分布的均值估计最可能的特征值，而方差表示特征值的不确定性。利用不确定性信息，可以自然地推导出匹配和融合PFEs的概率解。通过对不同基线模型、训练数据集和基准的实证评估表明，该方法通过将确定性嵌入转换为PFEs，可以提高确定性嵌入的人脸识别性能。PFEs估计的不确定性也可以作为潜在匹配精度的良好指标，这对于风险控制的识别系统非常重要。

 

1. Introduction

当人们被要求描述一张人脸图像时，他们不仅给出了面部特征的描述，还给出了与之相关的置信度。例如，如果图像中眼睛模糊，一个人会将眼睛的大小作为不确定的信息，并关注其他特征。此外，如果图像被完全损坏，无法识别任何属性，受试者可能会回应说他/她无法识别这张脸。这种不确定性(或置信度)估计在人类决策中是常见且重要的。

另一方面，在最先进的人脸识别系统中使用的表征通常都是置信度无关的。这些方法依赖于一个嵌入模型(例如深度神经网络)，在潜在特征空间中为每个人脸图像给出一个确定的点表征[27,35,20,34,4]。潜在空间中的一个点代表了模型对给定图像中人脸特征的估计。在估计误差有一定限制的情况下，两点之间的距离可以有效地度量相应人脸图像之间的语义相似度。但是在低质量输入的情况下，在图像中预期的面部特征是模糊的或不存在的，嵌入点的大偏移是不可避免的，导致错误识别(图1a)。

 

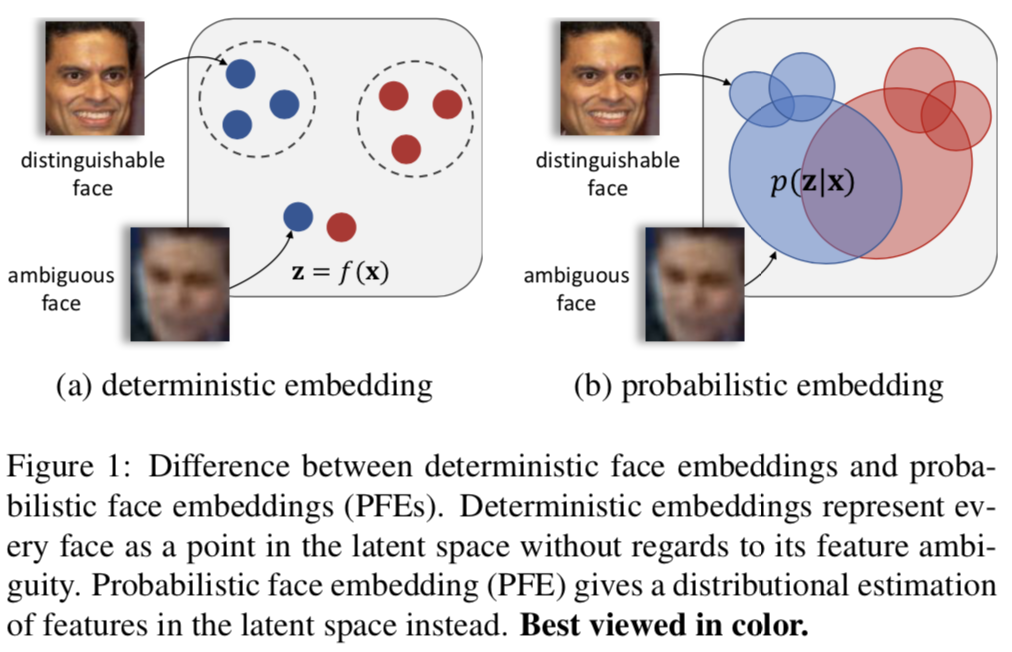
考虑到人脸识别系统已经在相对受限的人脸识别基准上得到了较高的识别精度,例如LFW[10]和YTF[37],其中大多数面部属性可以清楚地观察到,近期人脸识别的挑战已经开始考虑更多无约束的场景,包括监控视频[12,18,23](见图2)。在这些任务,任何类型和程度的变化都可能存在面对图像,其中大多数由特征模型学习的期望的面部特征可能是有缺陷的。由于信息的缺乏，不太可能找到一个特征集总是能够准确地匹配这些面孔。因此，在LFW上获得超过99%准确性的最先进的人脸识别系统在IARPA Janus基准上的性能大幅下降[18,23,12]。

 

为了解决上述问题，我们提出了Probabilistic Face Embeddings(PFEs)，它对每个输入人脸图像在潜在空间中进行分布估计，而不是点估计(图1b)。分布的均值可以被解释为最可能的潜在特征值，而分布的跨度则表示这些估计的不确定性。PFE可以从两个方面解决无约束人脸识别问题:(1)在匹配(人脸比较)过程中，PFE惩罚不确定的特征(维度)，而关注置信度高的特征。(2)对于低质量输入，PFE估计的置信度可用于拒绝输入或主动请求人工协助以避免错误识别。此外，可以推导出一种自然的解决方案，将一组人脸图像的PFE表征集合为一个新的具有较低不确定性的分布，以提高识别性能。PFE的实现是开源的。本文的贡献总结如下:

1. 一种感知不确定性的概率人脸嵌入(PFE)方法，它将人脸图像表示为分布而不是点。
2. 一种基于PFE的人脸匹配和特征融合的概率框架。
3.一种将现有确定性嵌入转换为PFEs的简单方法，无需额外的训练数据。
4. 综合实验表明，该方法能够提高确定性嵌入的人脸识别性能，有效滤除低质量的输入，增强人脸识别系统的鲁棒性。

 

2. Related Work

为了提高判别深度神经网络(DNNs)的鲁棒性和可解释性，深度不确定性学习受到越来越多的关注[14,5,15]。不确定性主要有两种类型:模型不确定性和数据不确定性。模型不确定性是指训练数据给定后，模型参数的不确定性，可以通过收集额外的训练数据来降低[22,24,14,5]。数据不确定性解释了输出的不确定性，其主要来源是输入数据的固有噪声，因此不能用更多的训练数据[15]来消除。本文研究的不确定度可分为数据不确定度。尽管技术已经发展到能在不同的任务中估计数据不确定性,包括分类和回归[15],他们不适合我们的任务,因为我们的目标空间没有明确地给定标签(虽然我们给定了身份标签,他们不能直接作为潜在特征空间中的目标向量)。变分自编码器[17]也可以看作是估算数据不确定性的一种方法，但它主要用于生成。对于人脸识别,一些研究[6,16,45]利用模型的不确定性进行人脸表征的分析和学习,但据我们所知,我们是第一个利用数据的不确定性(有些文献中也使用了术语“数据不确定性”去解决别的问题[40]))来做识别任务的。

 

Probabilistic Face Representation 将人脸建模为概率分布并不是一个新想法。在人脸模板/视频匹配领域，有大量的文献将人脸建模为概率分布[29,1]、子空间[3]或特征空间中的manifolds[1,11]。然而，这种方法的输入是一组人脸图像，而不是单一的人脸图像，他们使用分布之间的相似度或距离度量，例如KL-divergence，用于比较，但是这种方法不会惩罚不确定性。同时，也有研究[19,9]试图利用人脸parts的特征建立给定人脸的模糊模型。相比之下，所提出的PFE将每一张人脸图像表示为DNNs编码的潜在空间中的分布，我们使用感知不确定性的对数似然分数来比较这些分布。

 

Quality-aware Pooling  与上述方法相比，最近关于人脸模板/视频匹配的工作旨在利用深度CNN嵌入的显著性（saliency），将所有人脸的深度特征聚合成一个单一的紧凑向量[41,21,39,7]。在这些方法中，一个单独的模块学习去预测图像集中每个人脸的质量，然后归一化为特征向量的加权池。我们证明了在我们的框架下可以自然地推导出一个解决方案，这不仅为质量感知的池化方法提供了概率解释，而且还得到了一个更一般的解决方案，其中图像集也可以建模为PFE表征。

 

3. Limitations of Deterministic Embeddings

在本节中，我们从理论和经验两方面解释确定性人脸嵌入的问题。使用表示图像空间，表示维的潜在特征空间。一个理想的潜在空间应该仅编码身份显著的特征，并从与身份无关的特征中解耦出来。如此，每个身份就应该有一个独一的本质的编码，能够最好地表示这个人，且每个人脸图像是从采样的observation。训练人脸嵌入的过程可以看作搜索这样一个潜在空间和学习反向映射的关联过程。对于确定性嵌入，反向映射是一个Dirac delta函数 ，其中是嵌入函数。很明显，对于任何空间，给定x中噪音的可能性，要恢复精确的z值是不现实的，低质量输入的嵌入点不可避免地会偏离其固有z值(不管我们有多少训练数据)。

问题是这种偏移是否有界，使得我们的类内距离小于类间距离。然而，这对于完全不受约束的人脸识别是不现实的，我们进行了一个实验来说明这一点。让我们从一个简单的例子开始:给定一对相同的图像，一个确定性的嵌入将总是映射到相同的点，因此他们之间的距离将永远是0，即使这些图像不包含一个脸。这意味着“两张相似甚至相同的图片并不一定意味着它们属于同一个人的可能性很高”。

为了证明这一点，我们进行了一个实验，通过手工降低高质量图像，并可视化他们的相似度评分。我们从LFW数据集[10]中随机选择每个受试者的高质量图像，并手动向人脸插入高斯模糊、遮挡和随机高斯噪声。特别地，我们线性增加高斯核的大小，遮挡比和噪声的标准差来控制退化程度。在每个退化级别，我们使用64层CNN（trained on Ms-Celeb-1M [8] with AM-Softmax [33]）去提取特征向量，该模型可与最先进的人脸识别系统相媲美。将特征归一化到超球面嵌入空间。然后，报道了两种类型的余弦相似度结果:(1)原始图像对与各自退化图像之间的相似度，(2)不同身份的退化图像之间的相似度。如图3所示，对于所有三种类型的退化结果，真正的相似度分数下降到0，而impostor相似度分数收敛到1.0!这表明，在完全不受约束的情况下，即使模型非常自信(非常高/低的相似度分数)，也可能出现两种类型的错误:

(1) false accept of impostor low-quality pairs and
(2) false reject of genuine cross-quality pairs.

 

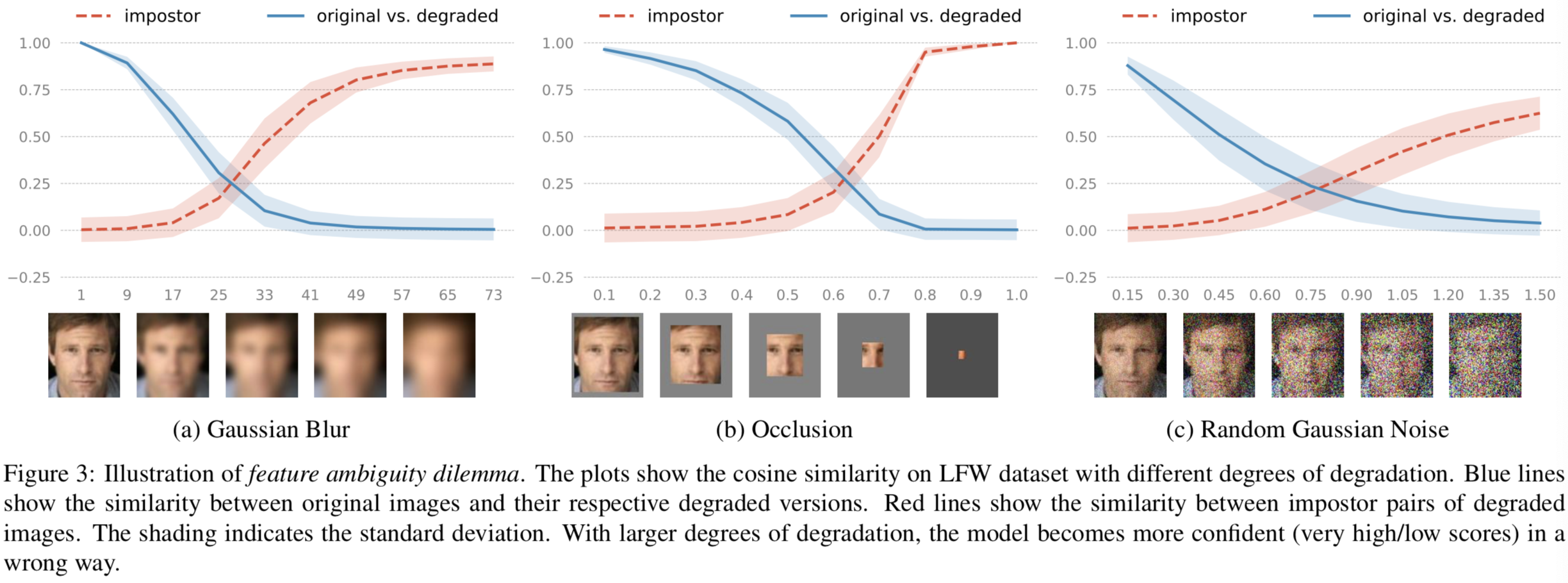
(左图的意思就是，在原始的确定性模型中，当属于同一个人的清晰图和模糊图对比时，模糊程度越大，两者的相似度越低（蓝线表示），即越容易被判别为不是同一个人；而当不属于同一个人的清晰图和模糊图对比时，模糊程度越大，两者的相似度越高（红线表示），即越容易被判别为是同一个人)

为了证实这一点，我们在IJB-A数据集上测试模型，发现impostor/genuine图像对分别对应最高/最低分数。这种情况与我们假设的完全一样(见图4)。我们将其称为Feature Ambiguity Dilemma，即当确定性嵌入被强制估计模糊人脸的特征时，就会出现这种情况。实验还暗示存在一个模糊输入映射到的dark space，且其距离度量是扭曲的。

 

4. Probabilistic Face Embeddings

为了解决上述由数据不确定性引起的问题，我们建议将不确定性编码到人脸表征中，并在匹配时加以考虑。具体来说，我们不是建立一个在潜在空间中进行点估计的模型，而是在潜在空间中估计一个分布来表示一个人的面孔的潜在外观（following the notations in Section 3）。具体说来，我们使用了多元高斯分布:

其中和都是第i个输入图像通过网络预测得到的D维向量。这里我们只考虑了一个对角协方差矩阵去减少人脸表征的复杂度。该表征应该有如下的特性：

  • 中心应该应该编码输入图像最重要的人脸特征
  • 不确定性应该编码每个特征维度的模型置信度

此外，我们希望使用单个网络来预测分布。考虑到训练人脸嵌入的新方法仍在开发中，我们的目标是开发一种方法，可以将现有的确定性人脸嵌入网络以一种简单的方式转换为PFEs。接下来，我们首先展示了如何比较和融合PFE表征来展示它们的优势，然后提出了我们学习PFEs的方法。

注1:由于篇幅的限制，我们在补充材料中提供了以下所有命题的证明。

 

4.1. Matching with PFEs

给定一对图像的PFE表征，我们可以直接测量他们是同一个人（共享相同的潜在编码）的"可能性":,其中。具体说明：

 

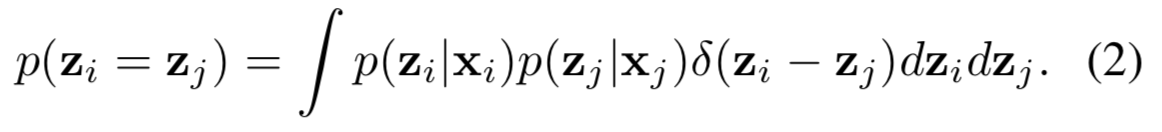
实际上，我们喜欢使用对数似然方法，所以解决方案将变为：

其中，表示的第维，表示的第维

注意，这个对称的度量可以被视为一个输入以另一个输入为条件的潜在编码的似然期望，也就是说

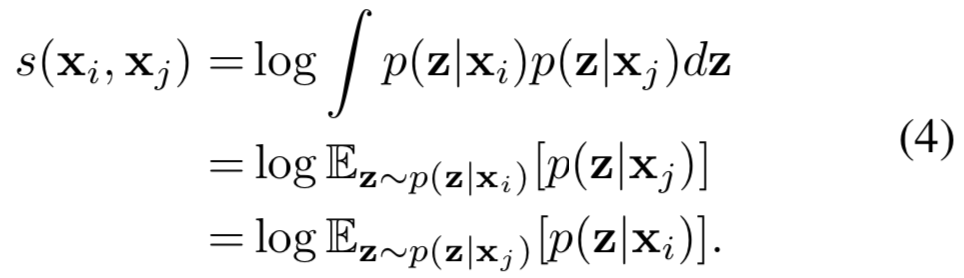
因此，我们称之为mutual likelihood score(MLS)。与KL-divergence不同，这个分数是无界的，不能被视为距离度量。可以证明，平方欧式距离等价于MLS中所有不确定度都相同的一种特殊情况:

Property 1. 如果对于所有数据来说是一个固定值，且维度为，MLS就等价于scaled and shifted负平方欧式距离。

此外，当不确定度允许不同时，我们注意到MLS有一些有趣的性质，使其不同于距离度量:
1. 注意机制:公式(3)中括号中的第一项可以看作是一个加权距离，它将更大的权重赋予更小的不确定维度。
2. 惩罚机制:式(3)中括号内第二项可视为惩罚项，惩罚具有较高的不确定性的维度。

3.如果或有大的不确定性，不管他们的均值之间的距离是多少，MLE的值都会比较低（因为惩罚）

4.只有当输入和有着小的不确定性，且他们的均值很接近，MLE才会高

最后的两个特性暗示了如果网络能够有效地估计，PFE就能够解决feature ambiguity dilemma

 

代码实现：

import tensorflow as tf

def negative_MLS(X, Y, sigma_sq_X, sigma_sq_Y, mean=False):
    with tf.name_scope('negative_MLS'):
        if mean:
            D = X.shape[1].value #size为[batch_size, embedding_size]

            Y = tf.transpose(Y) #[embedding_size, batch_size],转置才能实现输入i-j
            XX = tf.reduce_sum(tf.square(X), 1, keep_dims=True) #对维度1求和，keep_dims=True维持了维度1, [batch_size, 1]
            YY = tf.reduce_sum(tf.square(Y), 0, keep_dims=True) #对维度0求和，keep_dims=True维持了维度0，因为Y转置了，所以是维度0, [1, batch_size]
            XY = tf.matmul(X, Y) #[batch_size, batch_size]
            diffs = XX + YY - 2*XY #会自己广播扩维计算

            sigma_sq_Y = tf.transpose(sigma_sq_Y) #[embedding_size, batch_size]
            sigma_sq_X = tf.reduce_mean(sigma_sq_X, axis=1, keep_dims=True) #[batch_size, 1]
            sigma_sq_Y = tf.reduce_mean(sigma_sq_Y, axis=0, keep_dims=True) #[1, batch_size]
            sigma_sq_fuse = sigma_sq_X + sigma_sq_Y #[batch_size, batch_size]

            diffs = diffs / (1e-8 + sigma_sq_fuse) + D * tf.log(sigma_sq_fuse)

            return diffs
        else:
            D = X.shape[1].value #embedding_size
            X = tf.reshape(X, [-1, 1, D]) #[batch_size, 1, embedding_size]
            Y = tf.reshape(Y, [1, -1, D]) #[1, batch_size, embedding_size]
            sigma_sq_X = tf.reshape(sigma_sq_X, [-1, 1, D]) #[batch_size, 1, embedding_size]
            sigma_sq_Y = tf.reshape(sigma_sq_Y, [1, -1, D]) #[1, batch_size, embedding_size]
            sigma_sq_fuse = sigma_sq_X + sigma_sq_Y #[batch_size, batch_size, embedding_size],就能够得到所有i、j交叉求和的结果
            diffs = tf.square(X-Y) / (1e-10 + sigma_sq_fuse) + tf.log(sigma_sq_fuse) #等式(3)
            return tf.reduce_sum(diffs, axis=2) #返回[batch_size, batch_size]

def mutual_likelihood_score_loss(labels, mu, log_sigma_sq):

    with tf.name_scope('MLS_Loss'):

        batch_size = tf.shape(mu)[0]

        diag_mask = tf.eye(batch_size, dtype=tf.bool)
        non_diag_mask = tf.logical_not(diag_mask)

        sigma_sq = tf.exp(log_sigma_sq)
        loss_mat = negative_MLS(mu, mu, sigma_sq, sigma_sq) #返回的size为[batch_size, batch_size]，每个位置ij的值表示batch_i对batch_j的结果
        
        label_mat = tf.equal(labels[:,None], labels[None,:])
        label_mask_pos = tf.logical_and(non_diag_mask, label_mat) #得到类相同的mask

        loss_pos = tf.boolean_mask(loss_mat, label_mask_pos)#得到类相同的两个输入计算得到的loss
    
        return tf.reduce_mean(loss_pos)#然后计算他们的均值得到最后的损失结果
View Code

 

4.2. Fusion with PFEs

在很多情况下，我们有一个人脸图像模版（集），为了匹配，我们需要建立一个紧凑的表征。使用PFEs，可以导出用于表征融合的共轭公式(图5)。让表示一组来自相同身份的observations（人脸图像），且为第n个observation后的后验分布。然后，假设所有的observations是条件独立的（给定潜在编码z）。可以表示为：

 

其中是一个归一化因子。为了简化标注，我们在下面仅考虑一维的情况；解决方案很容易就能扩展为多变量的情况。

假设是一个无信息先验，即是一个方差接近的高斯分布，等式(5)的后验分布是有着更低的不确定性的新高斯分布（详情看补充材料）。接下来，给定一个人脸图像集，融合表征的参数能直接给出：

 

实际上，因为条件独立假设通常不为真，如视频帧有很多冗余，公式(7)会因集合中图像的数量而有偏差。因此，我们取维数最小值来获得新的不确定度。

 

该操作的代码实现：

def aggregate_PFE(x, sigma_sq=None, normalize=True, concatenate=False):
    if sigma_sq is None:
        D = int(x.shape[1] / 2)
        mu, sigma_sq = x[:,:D], x[:,D:]
    else:
        mu = x
    attention = 1. / sigma_sq #等式(7)
    attention = attention / np.sum(attention, axis=0, keepdims=True) #等式(7)
    
    mu_new  = np.sum(mu * attention, axis=0) #等式(6)
    sigma_sq_new = np.min(sigma_sq, axis=0) #取最小值做新的不确定度

    if normalize:
        mu_new = l2_normalize(mu_new)

    if concatenate:
        return np.concatenate([mu_new, sigma_sq_new])
    else:
        return mu_new, sigma_sq_new
View Code

 

Relationship to Quality-aware Pooling 如果我们考虑第i 个输入的所有维度共享相同的不确定性的情况，让质量值作为网络的输出。然后等式(6)可以写成：

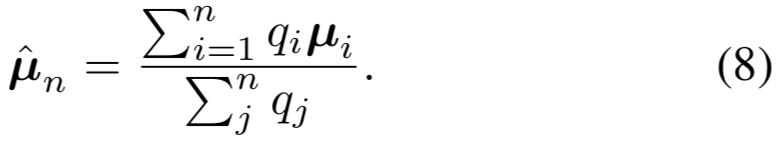
如果我们不使用融合后的不确定性，算法将与最近用于set-to-set 人脸识别的质量感知聚合方法相同[41,21,39]。

 

4.3. Learning

注意，对于任何确定性嵌入，如果进行适当的优化，能够切实地满足PFEs的特性：(1)嵌入空间是一个解耦的身份显著性潜在空间，(2)f(x)表示在潜在空间中给定输入最可能的特征。因此，本文考虑了一种阶段训练策略:给定一个预先训练好的嵌入模型f，固定其参数，使μ(x) = f(x)，并优化一个附加的不确定性模块来估计。当不确定性模块在嵌入模型的同一数据集上进行训练时，这种分阶段的训练策略比端到端学习策略能让我们在PFE和原始嵌入f(x)之间进行更公平的比较。

不确定性模块是由两个全连接层组成的网络，与bottleneck层共享相同的输入（bottleneck层即输出原始人脸嵌入的层）。优化准则是使所有真实对的相互似然得分最大化。形式上，损失函数最小化为：

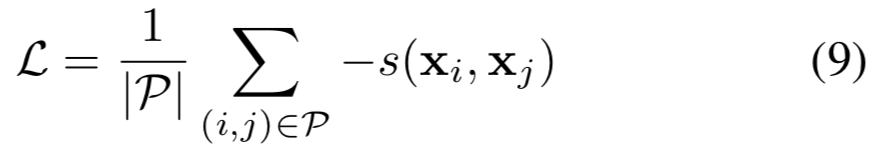
其中是所有真实对集，s函数定义在等式(3)中。在实际应用中，损失函数在每个mini-batch中都得到了优化。凭直觉,这个损失函数可以被理解为最大化p(z | x)的替代版:如果所有可能的真实对的潜在分布有很大的重叠, 那个对于任何关联的x，潜在目标z都应该有一个大的似然p(z|x)。注意到因为μ(x)是固定的,优化不会导致μ(x)崩溃成一个点。

 

额外：

MLE score的计算：

#sigma_sq1和sigma_sq2为输入的两个图的方差的平方
def pair_MLS_score(x1, x2, sigma_sq1=None, sigma_sq2=None):
    if sigma_sq1 is None:
        x1, x2 = np.array(x1), np.array(x2)
        assert sigma_sq2 is None, 'either pass in concated features, or mu, sigma_sq for both!'
        D = int(x1.shape[1] / 2)
        mu1, sigma_sq1 = x1[:,:D], x1[:,D:]
        mu2, sigma_sq2 = x2[:,:D], x2[:,D:]
    else:
        x1, x2 = np.array(x1), np.array(x2)
        sigma_sq1, sigma_sq2 = np.array(sigma_sq1), np.array(sigma_sq2)
        mu1, mu2 = x1, x2
    sigma_sq_mutual = sigma_sq1 + sigma_sq2
    dist = np.sum(np.square(mu1 - mu2) / sigma_sq_mutual + np.log(sigma_sq_mutual), axis=1)
    return -dist
View Code

 

5. Experiments

在本节中，我们首先在标准的人脸识别协议上测试提出的PFE方法，并与确定性嵌入进行比较。然后我们进行定性分析，以获得更多关于PFE行为的见解。由于篇幅限制，我们在补充材料中提供了实施细节。

为了综合评价PFEs的有效性，我们在7个基准上进行实验，包括著名的LFW[10]、YTF[37]、megface[13]和其他4个更不受约束的基准:

CFP[28]包含500名受试者的7000张正面(frontal)/侧面(profile)面部照片。我们只测试了frontal-profile(FP)协议，其中包括7000对frontal-profile脸。

IJB-A[18]是一个基于模板的基准测试，包含了500个受试者的25,813张人脸图像。每个模板包括一组静态照片或视频帧。与以前的基准相比，IJB-A中的人脸有更大的变化，并呈现出更不受约束的场景。

IJB-C[23]是IJB-A的扩展，具有3531个受试者的140740张面孔图像。IJB-C的验证协议包含了更多的impostor对，所以我们可以计算更低的False Accept Rates(FAR)下的True Accept Rates(TAR)。

IJB-S[12]是一个监控视频基准，包含350个监控视频，总时长30小时，5656个注册图像，和202个受试者的202个注册视频。该数据集中的许多人脸都是极端姿势或低质量的，使其成为最具挑战性的人脸识别基准之一(见图2示例图像)。

我们使用CASIA-WebFace[42]和MS-Celeb-1M[8]的cleaned版本（https://github.com/inlmouse/MS-Celeb-1M_ WashList.）作为训练数据，从中我们删除了同样包含在测试数据集中的受试者（CASIA-WebFace和MS-Celeb-1M分别删除了84和4182名受试者）

 

5.1. Experiments on Different Base Embeddings

由于我们的方法通过转换现有的确定性嵌入来工作，我们想评估它如何与不同的base嵌入工作（即均值的那个分支使用不同的预训练好的base嵌入，然后用来训练不确定分支），即用不同的损失函数训练的人脸表征。特别是，我们实现了以下最先进的损失功能:Softmax+Center Loss[35]，Triplet Loss[27]，A-Softmax[20]和AM-Softmax [33](我们也尝试着实现ArcFace[4]，但是在我们的例子中它并不能很好的收敛。所以我们没有使用它)。为了与之前的工作对齐[20,34]，我们在CASIA-WebFace数据集上使用各种损失函数训练一个64层残差网络[20]来作为基础模型。所有的特征都被l2归一化到一个超球面嵌入空间。然后我们在CASIA-WebFace上对每个基本模型的不确定性模块进行了3000个steps的训练。在LFW[10]、YTF[37]、CFP-FP[28]和IJB-A[18]四种不同的人脸识别标准下，对其性能进行了评价。结果如表1所示。在所有情况下，PFE都优于原始表示，表明该方法在不同的嵌入和测试场景下都具有鲁棒性。

  

5.2. Comparison with State-Of-The-Art

为了与最先进的人脸识别方法进行比较，我们使用了不同的基础模型，即在MS-Celeb-1M数据集上使用AM-Softmax训练的64层网络。然后我们固定参数，并在同一数据集上训练不确定性模块，进行12000 steps的训练。在接下来的实验中，我们比较了3种方法:

•Baseline 只使用64层确定性嵌入的原始特征和余弦相似度进行匹配。Average pooling用于模板/视频基准测试。

•PFEfuse 使用PFE中的不确定性估计σ和公式(6)来聚合模板的特征，但使用余弦相似度进行匹配。如果不确定性模块能够有效地估计特征的不确定性，那么通过赋予置信度大的特征更大的权重，与σ的融合应该能够比Average pooling的效果更好。

•PFEfuse+match 使用σ进行融合和匹配(与相互的似然分数)。根据式(6)和式(7)融合模板/视频。

在表2中，我们展示了三个相对简单的基准测试的结果:LFW、YTF和megface。虽然在LFW和YTF上的精度接近饱和，但所提出的PFE仍然提高了原始表示的性能。注意，megface是一个有偏数据集:因为所有的探头都是来自FaceScrub的高质量图像，所以megface中的positive对都是高质量图像，而negative对最多只包含一个低质量图像（验证协议中megface的negative对仅包括探头与干扰物之间的negative对）。

 

 

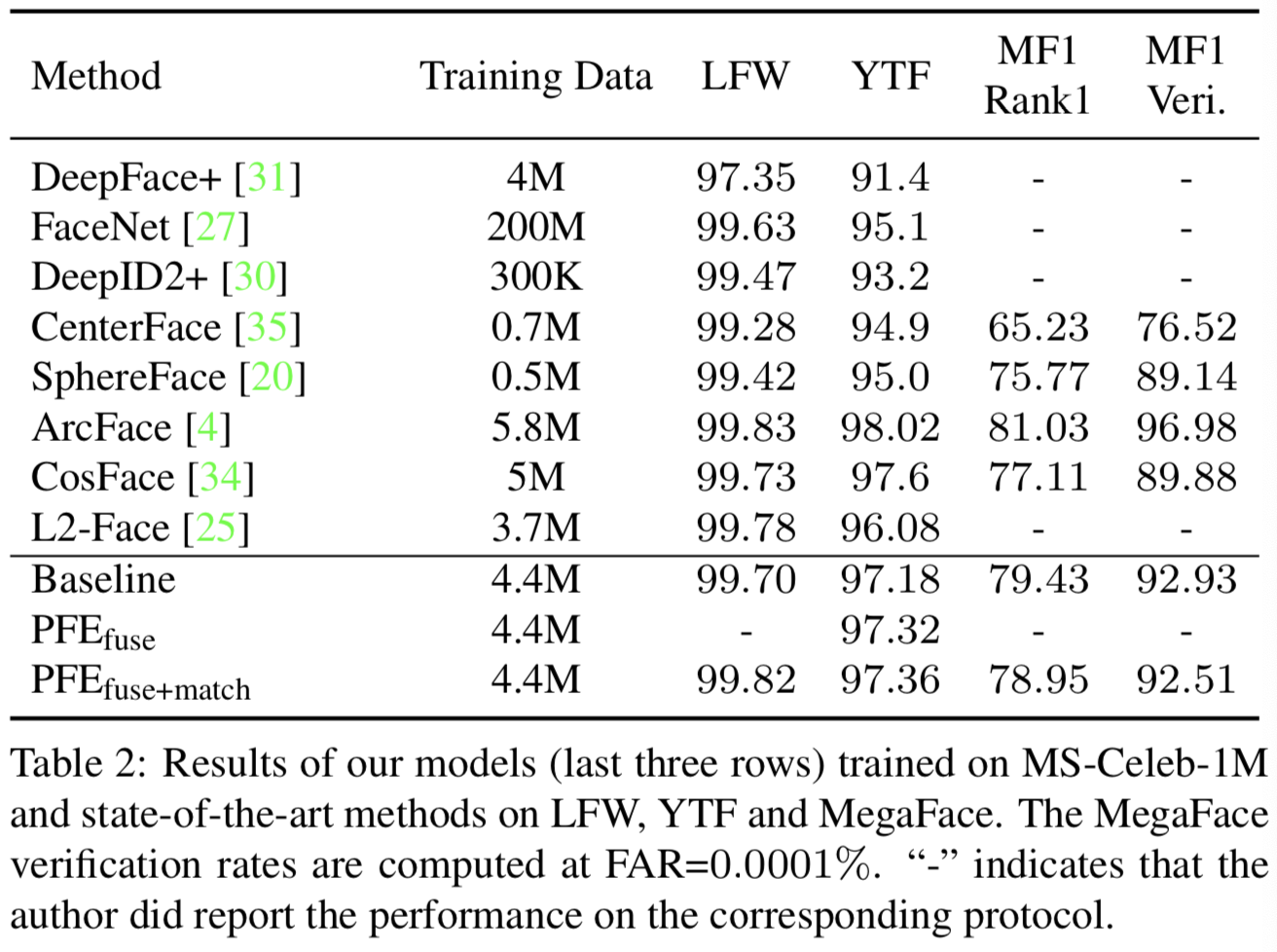
因此，由feature ambiguity dilemma(第3节)引起的这两种错误都不会在MegFace中出现，因此它自然倾向于确定性嵌入。然而，在这种情况下，PFE仍然保持性能。我们也注意到这样的bias，即目标图库的图像比其他图库的图像质量更高，但这种情况在现实世界的应用程序中是不存在的。

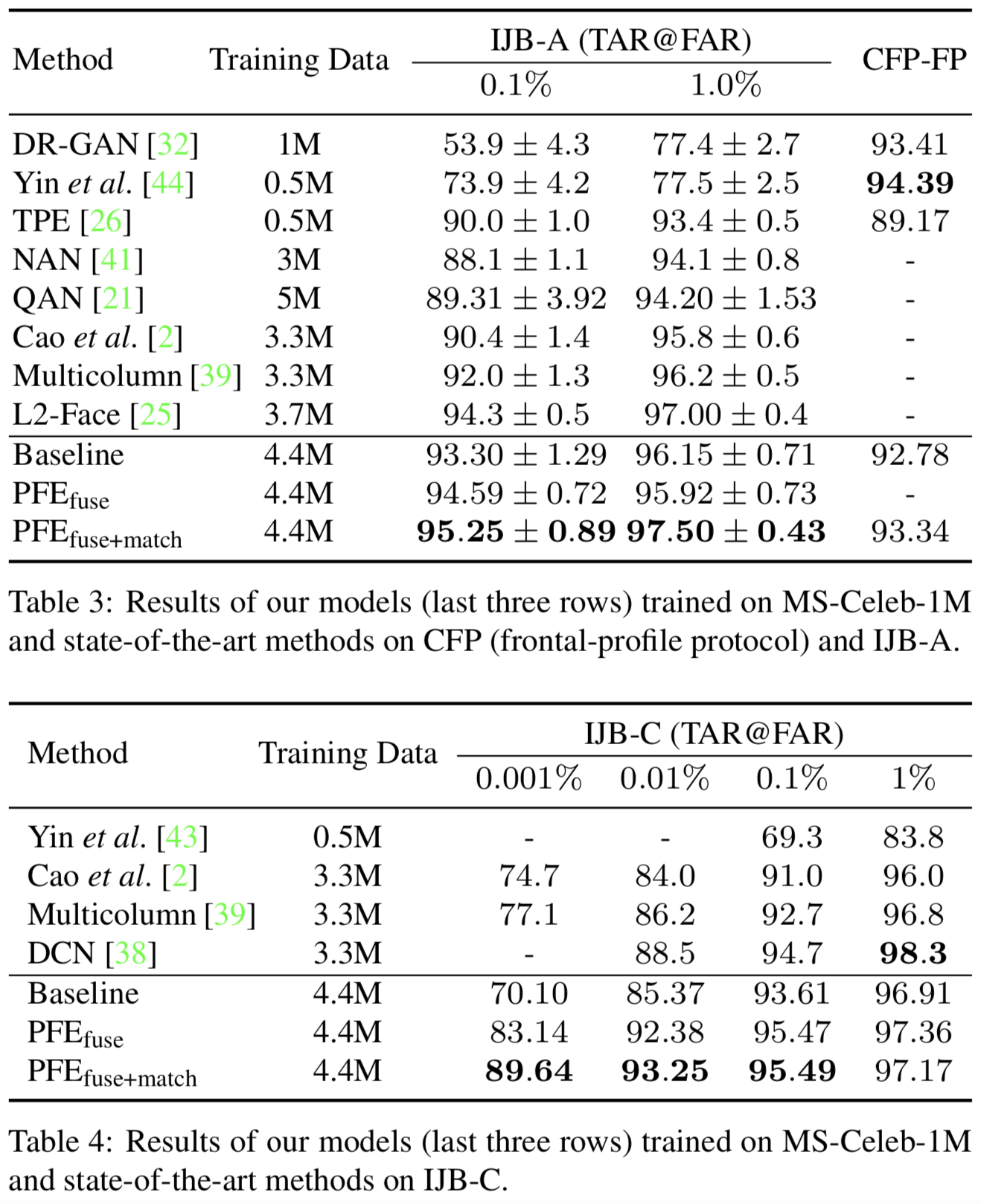
在表3和表4中，我们展示了在三个更有挑战性的数据集上的结果:CFP、IJB-A和IJB-C。这些数据集中的图像在姿态、遮挡等方面有更大的变化，面部特征可能更模糊。因此，我们可以看到PFE在这三个基准上取得了更显著的改善。特别是在FAR= 0.001%的IJB-C上，PFE降低了64%的错误率。此外，简单地将原始特征与学习到的不确定性(PFEfuse)融合在一起也有助于性能的提高。

 

在表5中，我们报告了最新基准测试IJB-S的三个协议的结果。同样，在大多数情况下，PFE能够提高性能。请注意，“Surveillance-to-stil”和“Surveillance-to-booking”中的图库模板都包含了高质量的正面大头照，几乎没有特征的模糊性。因此，我们在这两个协议中只看到了轻微的性能差距。但在最具挑战性的“surveillance-to-surveillance”协议中，利用不确定性进行匹配可以实现更大的改进。PFEfuse+match在所有open-set协议上均显著提高了性能，说明MLS对absolute pairwise score的影响大于对relative ranking的影响。

  

5.3. Qualitative Analysis

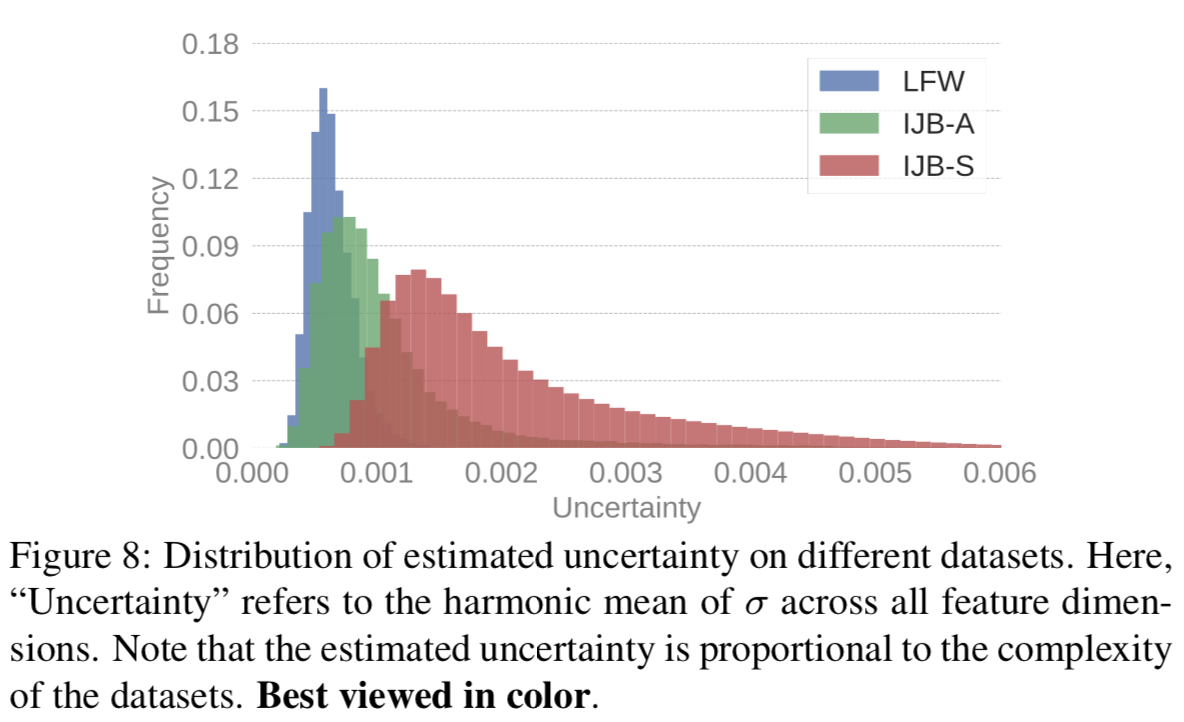
Why and when does PFE improve performance? 我们首先在第3节中使用PFE表征和MLS重复相同的实验。这里的基本模型使用的是相同的网络。从图6中可以看出，尽管低质量impostor对的分数仍在增加，但它们收敛到一个低于大多数genuine分数的点。类似地，cross-quality genuine对的分数收敛到一个点，比大多数impostor的分数更高。这意味着PFE可以解决第3节中讨论的两种类型的错误。图7中的IJB-A结果进一步证实了这一点。图8显示了LFW、IJB-A和IJB-S的估计不确定性的分布。可以看到，不确定性的“方差”按以下顺序增加:LFW < IJB-A < IJB-S。对比5.2节的性能，我们可以看到PFE在图像质量更多样化的数据集上，性能有更大的提升。

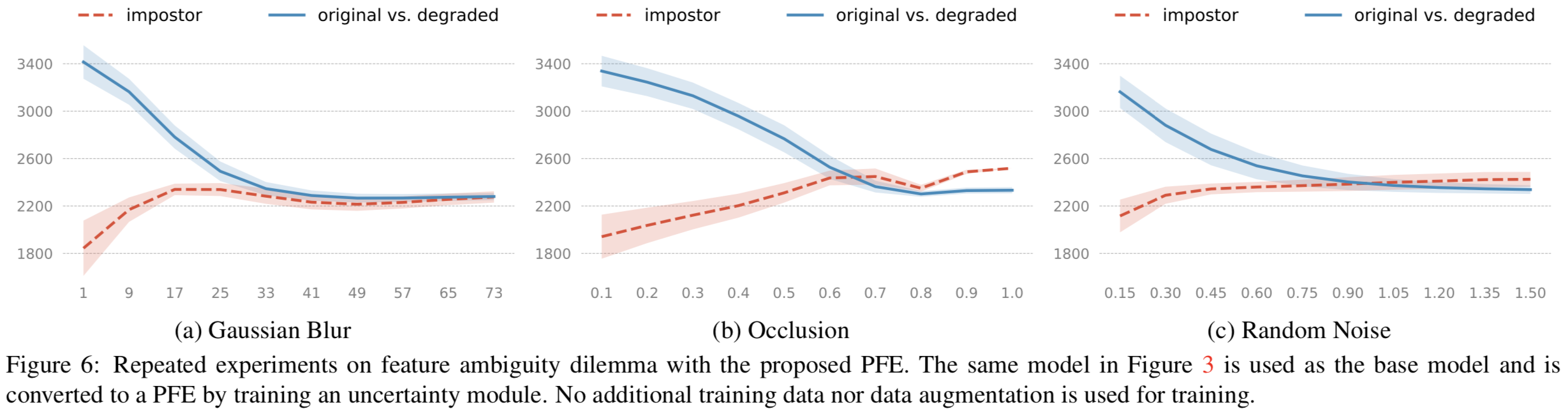
 (左图说明了，在我们设计的PFEs模型中，当属于同一个人的清晰图和模糊图对比时，模糊程度越大，两者的MLS相似度变低了，但是没有变得很低（蓝线表示）；而当不属于同一个人的清晰图和模糊图对比时，模糊程度越大，两者的MLS相似度会变高（红线表示），但是也没有变得很高。证明这种计算图像相似度的新metric在面对低质量图片时更加鲁棒)

 

 

What does DNN see and not see?  要回答这个问题,我们在原始embedding上训练一个解码网络,然后通过从给定x的估计分布p(z|x)中采样z来把它应用到PFE。高质量的图像(图9行1),重建的图像往往是非常一致的没有太多变化,暗示在这个图像模型能够得到非常确定的面部特征。相比之下，对于低质量的输入(图9第2行)，可以从重构图像中观察到更大的变化。特别地，可以从图像中清晰识别的属性(例如，浓眉)仍然是一致的，而不能识别的属性(例如，眼睛形状)有更大的变化。对于误检的图像(图9 Row 3)，重构图像中可以观察到明显的变化:在给定的图像中，模型没有看到任何显著的特征。

 

6. Risk-controlled Face Recognition

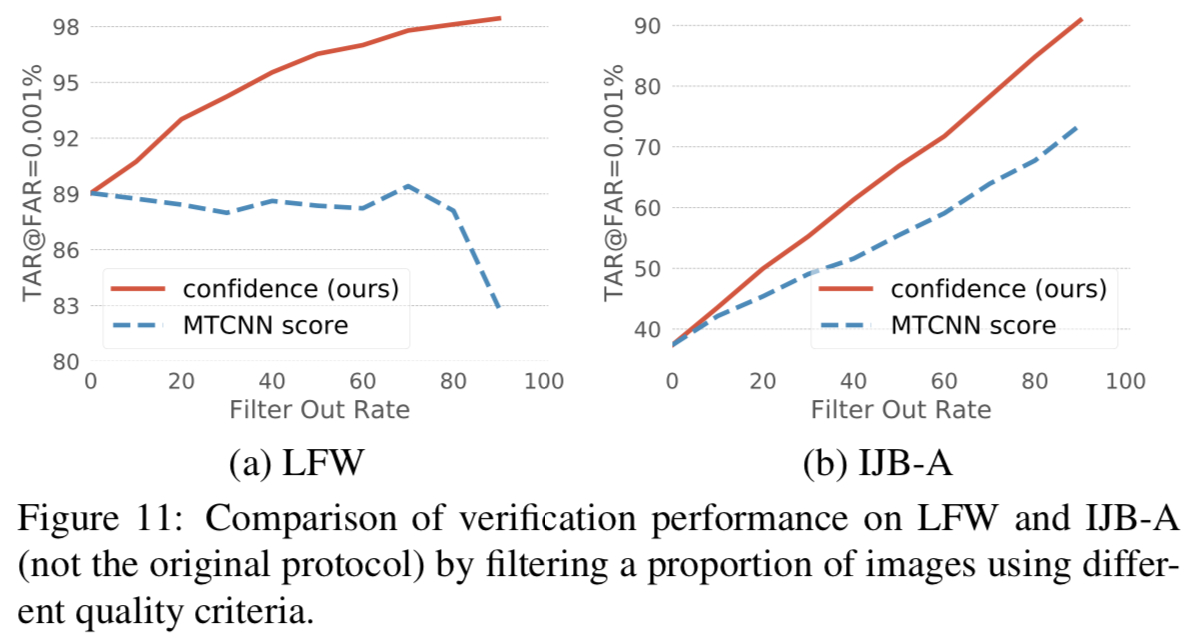
在许多场景中，我们可能期望系统能够实现更高的性能，或者在面对复杂的应用程序场景时，我们可能希望确保系统的性能能够得到控制。因此，我们希望模型能在不确定的情况下拒绝输入图像。一个常见的解决方案是使用质量评估工具对图像进行过滤。我们证明PFE为这个任务提供了一个自然的解决方案。我们从LFW和IJB-A数据集获取所有图像，用于图像级人脸验证(我们在这里没有遵循原始协议)。该系统允许“filter out”所有图像的一部分，以保持更好的性能。然后我们报告TAR@FAR= 0.001%的“Filter Out Rate”。我们考虑两个过滤标准:(1)MTCNN[36]的检测分数(2)我们的不确定性模块预测的置信度值。在这里，第i个样本的置信度被定义为在所有维度上的harmonic均值的逆。为了公平性，两种方法都使用了原始确定性嵌入表征和余弦相似度进行匹配。为了避免饱和的结果，我们使用了在CASIA-WebFace上训练的模型和AM-Softmax。结果如图11所示。可以看出，预测的置信度值可以更好地反映输入图像的潜在识别精度。这是一个预期的结果，因为PFE是在监督下为特定模型训练的，而外部质量估计器不知道模型匹配使用的特征类型。具有高/低 可信度/质量分数的示例图像如图10所示。

 

7. Conclusion

我们提出了probabilistic face embeddings(PFEs)方法，它将人脸图像表示为潜在空间中的分布。推导出概率解来比较和聚合人脸图像的PFE。与确定性嵌入算法不同，PFEs算法在无约束人脸识别中不存在特征模糊问题。通过对不同设置的定量和定性分析表明，将确定性嵌入转化为PFEs可以有效提高人脸识别性能。我们还表明，PFEs中的不确定性对人脸图像的“判别”质量来说是一个很好的指标。在未来的工作中，我们将探索如何以端到端的方式学习PFEs，以及如何解决人脸模板中的数据依赖性。

 

posted @ 2021-03-31 14:43  慢行厚积  阅读(2719)  评论(0)  编辑  收藏  举报