采样方法 - Sampling Matters in Deep Embedding Learning（Distance weighted sampling） - 1 - 论文学习

 

论文链接：https://arxiv.org/abs/1706.07567

开源代码：https://github.com/chaoyuaw/incubator-mxnet/tree/master/example/gluon/embedding_learning

Sampling Matters in Deep Embedding Learning

Abstract

深度嵌入（embeddings）回答了一个简单的问题:两幅图像有多相似?学习这些嵌入是验证、zero-shot学习和可视化搜索的基础。最突出的优化深度卷积网络的方法是使用合适的损失函数，如contrastive损失或triplet损失。虽然大量的工作只集中在损失函数上，但我们在本文中表明，选择训练样本的方法也起到同样重要的作用。我们提出了距离加权抽样（distance weightedsampling）方法，它选择了比传统方法有着更多的信息和更稳定的例子。此外，我们证明了一个简单的基于边际损失足以胜过所有其他损失函数。我们在Stanford Online Products，CAR196，和CUB200-2011数据集上评估我们的方法在图像检索和聚类的效果，以及在LFW数据集上评估人脸验证的效果。我们的方法在所有这些方面都达到了最先进的性能。

 

1. Introduction

将图像转换成丰富的语义表征的模型是现代计算机视觉的核心，其应用范围从zero-learning学习[5,41]和视觉搜索[3,10,22,29]，到人脸识别[6,23,25,28]或细粒度检索[22,28,29]。经过训练以尊重pairwise关系的深度网络已成为最成功的嵌入模型[4,6,25,34]。

深度嵌入学习的核心思想很简单:将相似的图像在嵌入空间中拉近，将不同的图像分开。例如，contrastive损失[11]迫使所有的positive图像接近，而所有的negatives应该被分开一定的固定距离。然而，对所有图像使用相同的固定距离是非常有限制的，阻止了嵌入空间中的任何扭曲。这就导致了triplet损失的出现，其只需要在每个例子[25]的基础上，使得negative图像比positive图像更远即可。triplet损失是目前标准嵌入任务中表现最好的损失之一[22,25,45]。与pairwise损失不同的是，triplet损失不仅改变了孤立的损失函数，还改变了正样本和负样本的选择方式。这就给我们提供了两个问题:损失和采样策略的选择。如图1所示。

（这篇论文给的采样方法为Distance weighted sampling， 损失为margin based loss）

 

 

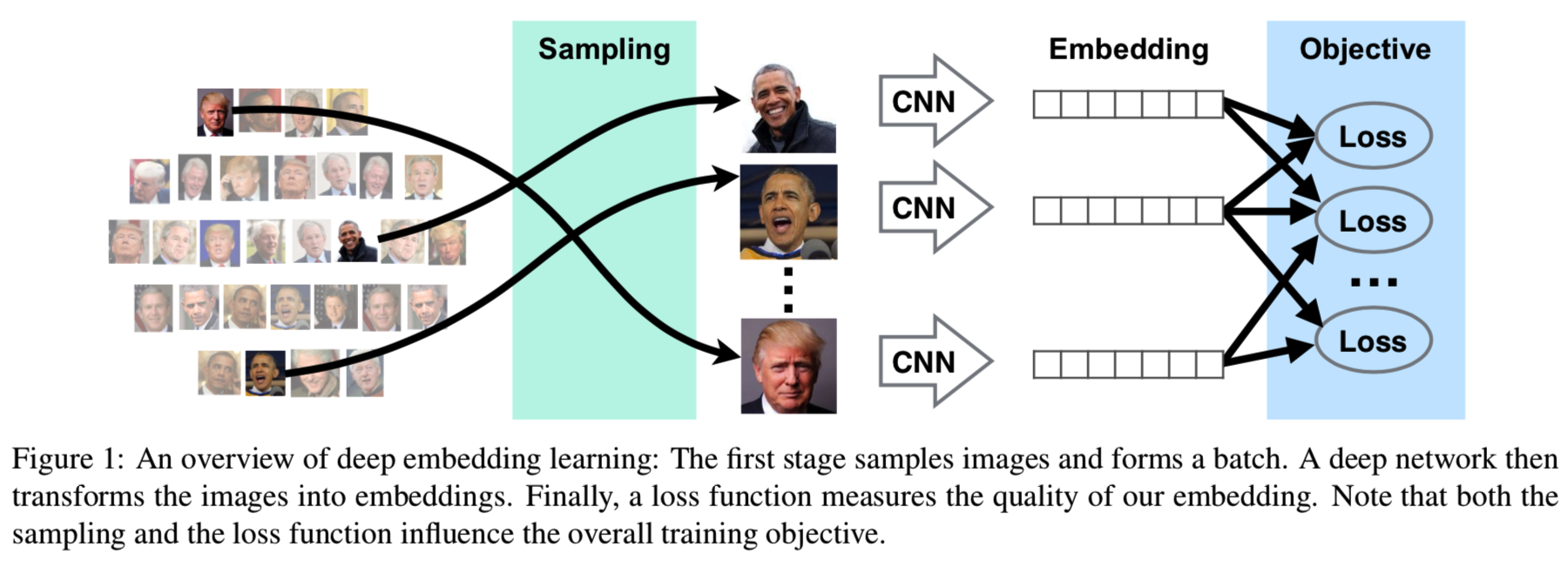
在本文中，我们证明了样本选择在嵌入学习中所起的作用与样本损失的作用相同或更重要。例如，对于相同的损失函数，不同的采样策略会导致截然不同的解决方案。同时，在良好的采样策略下，许多不同的损失函数的表现相似:如果使用相同的采样策略，contrastive损失和triplet损失的效果几乎一样好。在本文中，我们分析了现有的抽样策略，并说明了它们为什么有效和为什么无效。然后，我们提出了一种新的抽样策略，即根据样本之间的相对距离均匀地抽取样本。这就纠正了嵌入空间的几何形状所引起的偏差，同时保证了任何数据点都有被采样的机会。我们提出的采样导致了较低的梯度方差，从而稳定了训练，导致质量更好的嵌入，而不用考虑损失函数。

损失函数显然也很重要。我们提出了一个简单的基于边际的损失作为contrastive损失的扩展。它只鼓励所有的正样本在一个距离内，而不是尽可能接近。它放宽了损失，使它更有活力。此外，通过使用isotonic回归，我们的边际损失关注的是相对顺序而不是绝对距离。

我们基于边际损失和距离加权抽样的方法在Stanford Online Products、CARS196和CUB200-2011数据集上实现了最先进的图像检索和聚类性能。它也优于以前在使用标准公开可用的训练数据的LFW人脸验证数据[16]上的最先进的结果。我们的损失函数和采样策略都是易于实现且训练有效的。

 

2. Related Work

利用神经网络提取某些关系特征的想法可以追溯到90年代。Siamese网络[4]找到一个嵌入空间，这样类似的例子有类似的嵌入，反之亦然。这种网络是端到端训练的，在所有映射之间共享权值。Siamese网络首先应用于签名验证，后来扩展到人脸验证和降维[6,11]中。然而，考虑到当时有限的计算能力和它们的非凸特性，这些方法最初并没有受到太多关注。convex方法更为流行[7,39]。例如，triplet损失[26,36]就是凸优化中出现的最突出的方法之一。

有了足够的数据和计算能力，这两个学派的思想结合成一个使用triplet损失的Siamese结构。这使得人脸验证的表现接近人类[23,25]。受triplet损失启发，一些人对更多的例子实施了限制。例如，PDDM[15]和直方图损失[34]使用了quadruplets。除此之外，n-pair损失[28]和Lifted Structure[22]定义了一个batch中所有图像的约束条件。

这种过多的损失函数很容易让人想起信息检索中的排序问题。有一个individual、pair-wise[14]，和list-wise[35]方法的组合被用来最大化相关性。值得注意的是isotonic回归方法，它解开了pairwise比较的纠缠，从而提高了计算效率。有关概述，请参阅[21]。

一些论文探讨了其他性质的建模。Structural Clustering[29]优化了集群质量。PDDM[15]提出了一种新的构建局部特征结构的模块。HDC[41]训练一个集成来建模不同“hard levels”的例子。相反，我们在这里表明，如果与正确的抽样策略配对，一个简单的pairwise损失就够用了。

样本选择技术的研究相对较少。对于contrastive损失，通常从所有可能的对中随机选择[3,6,11]，有时采用难负样本挖掘（hard negative mining）[27]方法。对于triplet损失，广泛采用在FaceNet[25]中提出的semi-hard negative mining方法[22,23]。以加速收敛到相同的全局损失函数为目标，研究了随机优化[43]的抽样问题。相反，在嵌入学习中，采样实际上改变了考虑的整体损失函数。在这篇文章中，我们展示了采样如何影响实际的深度嵌入学习的表现。

 

3. Preliminaries

让f(x_i)表示一个数据点的embedding，其中是一个带有参数Θ的可微深度网络。为了训练的稳定[25]，f(x_i)经常被归一化到单位长度。我们的目标是学习一个embedding去让相似数据点更接近，同时将不相似数据点分开。形式上来说，我们定义两个数据点之间的距离为，其中||.||表示欧式范数。对于任意y_ij=1的正数据点对，其距离应该小；对于y_ij=0的负数据点对，距离应该大。

 

contrastive损失通过鼓励所有正对距离接近0，并保持负对距离在一定的阈值之上的方法直接优化了这个距离:

contrastive损失的一个缺点是我们必须为所有的负样本对选择一个恒定的边界α。这意味着视觉上不同的类与视觉上相似的类一样嵌入在同样小的空间中。嵌入空间不允许扭曲。

相比之下，triplet损失只是试图保持每个样本的所有的正对都比其任意负对更接近样本:

这种形式允许嵌入空间被任意扭曲，并且不施加一个恒定的边界α限制。

从风险最小化的角度来看，我们的目标可能是分别优化所有O(n²) pairs或O(n³) triplets的总损失。这是：

 

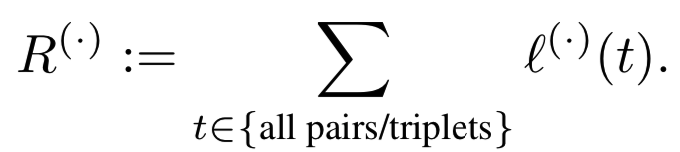
这在计算上是不可行的。此外，一旦网络收敛，大多数样本的贡献很小。

这导致了许多加速收敛的heuristics的出现。对于contrastive损失，hard negative mining通常具有较快的收敛速度。对于triplet损失，则不那么明显，因为hard negative mining往往会导致模型崩溃，即所有图像的嵌入都是相同的。因此，FaceNet[25]提出使用一种有点神秘的semi-hard negative mining:给定一个anchor a和一个正例p，通过：

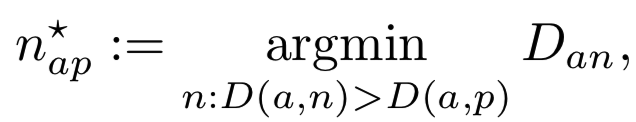
在一个batch中获得一个负例n。这样会产生一个违反规则的示例，这个示例是hard的，但还不算too hard。batch构建也很重要。为了获得更多信息的triplet，FaceNet batch size设置为1800，并确保每个identity在batch[25]中大约有40幅图像。甚至如何在一个batch中最好地选择triplets也不是很清楚。Parkhi等人[23]使用在线选择方法，因此每一对(a, p)只抽样一个triplet。OpenFace[2]采用了离线triplet选择，因此一个batch中有三分之一的图像分别作为anchor、正例和负例。

 

简而言之，抽样很重要。它通过加权样本隐式地定义了一个相当heuristic的目标函数。这种方法使得复制和扩展insights到不同的数据集、不同的优化框架或不同的体系结构变得困难。在下一节中，我们将分析其中一些技术，并解释为什么它们能够提供更好的结果。然后，我们提出了一种新的采样策略，以超越当前的最先进结果。

 

4. Distance Weighted Margin-Based Loss

为了理解均匀采样负例时发生了什么，回想一下我们的嵌入值通常被限制在n维单位球中，n≥128。考虑这些点在球上均匀分布的情况。在这种情况下，pairwise距离的分布如下：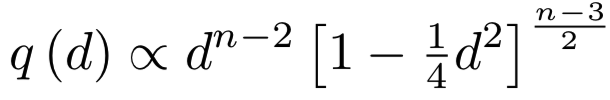

推导可见[1]。图2展示了测量出现的集中情况。实际上，在高维空间中，q(d)接近。另一方面来说，如果负样本均匀分散，且对其随机采样，我们可能会获得的样本（即远离的样本）。对于小于的阈值，其将导致无损失产生，因此学习没有进展。已学习的嵌入遵循非常类似的分布，因此也适用于相同的推理。详见补充材料。

 

too hard的负例会引起另一个问题。考虑一个负对t:= (a, n)或一个triplet t:= (a, p, n)。关于负例f(x_n)的梯度为：

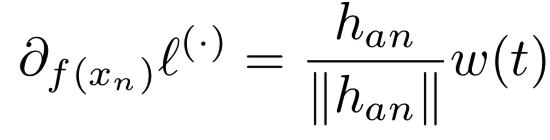
用于一些函数w(.)和。第一项决定梯度的方向。当|| h_an ||比较小时，会出现一个问题，且我们embedding的估计是有噪音的(意思是负样本距离太小则负样本的梯度方向容易受噪声影响，梯度大小接近于0。 所以可能既走不动又可能走错，距离太大则没有意义，所以会需要各个距离的，那为了得到各种距离的，最直接就是采样的概率与出现的概率成反比) 。给定充足地由训练算法引入的噪音z，方向被噪音控制。图3a显示了用于梯度方向的协方差矩阵的核范数。我们可以看到，当负例太close/hard时，梯度方差大（方差低才好），信噪比低。与此同时，随机样本往往相距太远，不能产生良好的信号。

 

  

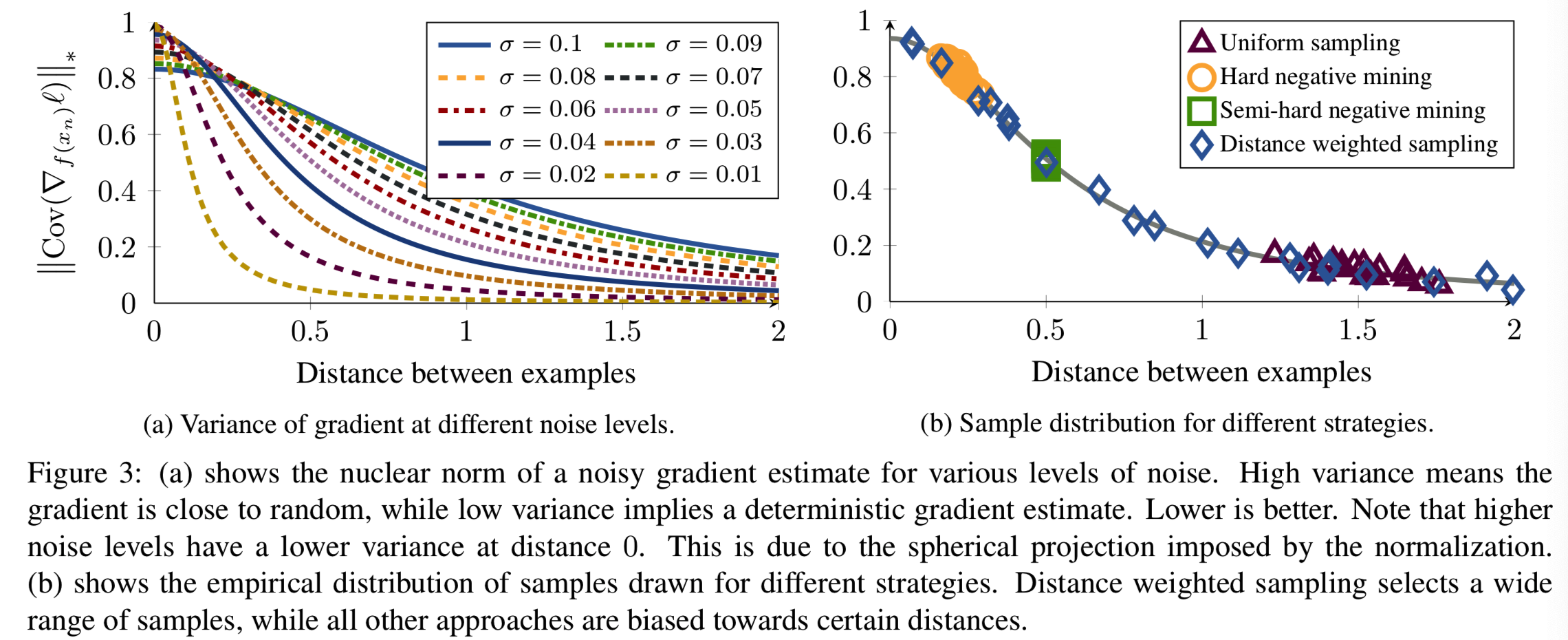
Distance weighted sampling. 因此，我们提出了一个新的采样分布，纠正偏差，同时控制方差。具体来说，我们按距离均匀采样，即使用权值为q(d)⁻¹的采样。这给了我们分散，而不是聚集在一个小区域的例子。为了避免噪声样本，我们对加权样本进行了剪切（即距离太小或太大的负例会被去掉）。形式上,给定一个anchor 样例a, 使用下面公式距离加权采样 样本负对(a, n*)：

（以图2举例，即如果距离D_an远离（即小于或大于），这样q(D_an)越小的，q^-1(D_an)的值则越大，只要不大于λ，则取其为该负例被选取的概率；因此可知远离但又不是很远，即D_an没小到接近0或大到特别大的情况下的负例被采样的概率最高。如果距离D_an接近，则q(D_an)值比较大，因此q^-1(D_an)的值比较小，选取这种负样本的概率小。

总结就是，因为距离D_an接近的负例多，因此其选取概率低；远离的负例少，因此选取的概率高。这样就能均衡选取到相近数量的各种距离D_an的负例）

 

图3b对比了不同策略下得到的模拟样例的梯度变化情况。hard negative mining总是在高方差区域（负例距离太近）提供实例。这导致了噪声梯度，不能有效地分开两个例子，因此得到一个爆炸模型。随机抽样只产生不造成损失（负例距离过大）的简单例子。semi-hard negative mining在两者之间找到一个狭窄的集合。虽然它可能在开始时迅速收敛，但在某些时候，band内没有留下任何例子，网络将停止前进。FaceNet报告了一个一致的发现:在某个点之后，损失的减少速度急剧减慢，他们的最终系统花了80天来训练[25]。距离加权抽样提供了广泛的样本，从而在控制方差的同时稳定地产生信息样本。在第5节中，我们将看到距离加权抽样在几乎所有测试的损失函数中都带来了性能改进。当然，抽样只能解决一半的问题，但它使我们能够分析各种损失函数。

 

图4a和图4b描述了contrastive损失和triplet损失。有两个关键的区别，这通常解释了为什么triplet损失优于contrastive损失:triplet损失没有假设一个预定义的阈值来分离相似和不同的图像。相反，它可以灵活地扭曲空间以容忍outliers，并适应不同类的不同级别的类内差异。第二，triplet损失只要求正例比负例更接近，而contrastive损失则需要努力将所有正例尽可能接近。后者是不必要的。毕竟，对于大多数应用程序，包括图像检索、聚类和验证，维护正确的相对关系就足够了。

 

（纵轴是损失，横轴是样本对距离。蓝色表示的就是当正对距离越小越接近于0时，梯度变化就越小，对模型更新影响小；越大则梯度变化大，对模型更新影响大。绿色即表示负对距离过小时，说明这是个hard negative，所以梯度变化就大，对模型更新影响大；但是如果距离过大，那么梯度接近0，说明这个负对没什么用）

（举例说明，可见图4(c)对应的就是下面的式子，图的结果的意思是：当正对距离D_ap小于D_an-α时，正对的梯度为0，大于则梯度为1；当负对距离D_an小于D_ap-α时，梯度为-1，大于时梯度为0）

另一方面，在图4b中，我们也观察到，在负例中，triplet损失的损失函数呈凹形。特别要注意的是，对于hard negatives(带有小D_an)，相应的负例的梯度接近于零。在这种情况下，不难看出为什么hard negative mining会导致一个崩溃的模型:因为hard positive pairs给出了很大的吸引梯度，而hard negative pairs给出了很小的排斥梯度，所以所有点最终聚集到同一个点。为了使来自所有距离的例子的损失稳定，一个简单的补救方法是使用而不是，即：

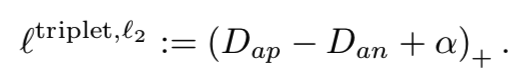
图4c显示了该损失函数。它对于任何嵌入f(x)的梯度长度都是1。关于使用固定长度梯度的好处的更多讨论见例[12,20]。如第5节所示，这种简单的固定加上距离加权抽样方法的效果已经超过了传统的triplet损失。

 

Margin based loss. 这些观察激励我们设计一个损失函数，该函数享有triplet损失的灵活性，其有一个适合于来自所有距离例子的形状，同时提供了contrastive损失的计算效率。其基本思想可以追溯到ordinal回归中，即只有分数的相对顺序是重要的[17]。也就是说，我们只需要知道两个集合之间的交叉。Isotonic回归通过分别估计阈值来利用这一点，然后对相对于阈值的分数进行惩罚。我们使用相同的技巧，现在应用于pairwise距离而不是分数函数。基于边际的自适应损失定义为：

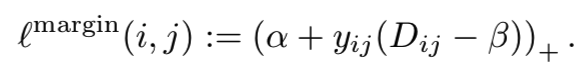
（所以对于正对来说，损失为α+ Dap - β；而对于负对来说，损失变为α- D_an + β，当D_ij=β时，损失相等。图4(d)的意思是当正对距离Dap小于 β-α 时，此时损失小于0，梯度为0；大于β-α时梯度才为1。当负对距离D_an小于β+α时，梯度为-1；大于则损失小于0，梯度为0）

（所以并不要求所有正例尽可能的小（这里要求大于β-α），因为有时候要允许类内的差异（细粒度识别），而且有时候任务只需要相对关系（图像检索））

在这里，β是一个变量，它决定正对和负对之间的边界，α控制分离的边界，而y_ij∈{−1,1}。图4d显示了这个新的损失函数。我们可以看到，它与contrastive损失相比，放宽了对正例的限制。它有效地在位移距离D_ij−β上施加了很大的边际损失的。这种损失与支持向量分类器(SVC)[8]非常相似。

为了享受类似triplet损失的灵活性，我们需要一个更灵活的边界参数β，它依赖于特定类β^(class)和特定样本β^(img)项。

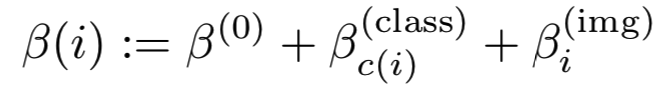
尤其是，特定样本偏差在triplet loss中和阈值是一样的角色。手动选择所有的和是很不灵活的。相反，我们想要共同学习这些参数。幸运的是，β的梯度可以简单地计算为：

 很明显，更大的β值更可取，因为它们可以更好地利用嵌入空间。因此，为了正则化β，我们引入了超参数v，这导致了优化问题最终为：

在这里，算法调整了违反左右边界的点数量之间的差异。这可以通过观察到它们的梯度需要在一个最佳β中抵消来看出。请注意，这里使用的v非常类似于v-svm[24]中的v技巧。

 

Relationship to isotonic regression. 优化基于边际的损失可以看作是解决一个距离排序问题。从技术上讲，它与信息检索[21,44]中的排序学习问题相似。为了查看第一个注意事项-最佳β，经验风险可以写为：

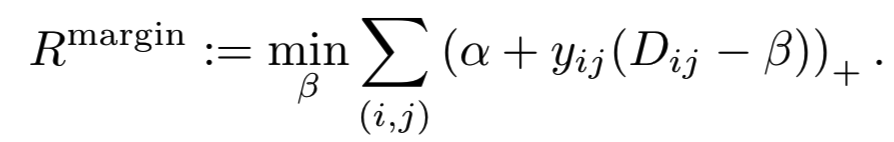
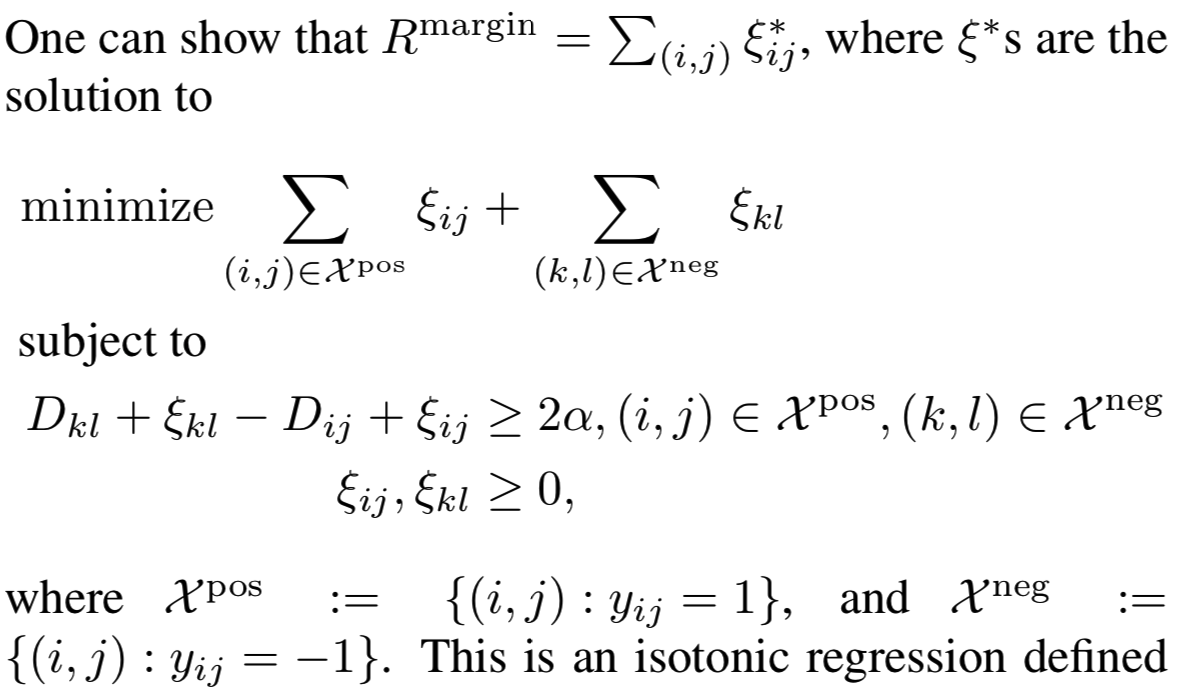
这是一个定义在绝对误差上的isotonic回归。我们看到，基于边际损失是保持相对orders的“minimum-effort”更新的数量。它侧重于相对关系，即侧重于正对距离和负对距离的分离。这与传统的损失函数(如contrastive损失)相反，在contrastive损失函数中，损失是相对于预定义的阈值定义的。

 

5. Experiments

对该方法在图像检索、聚类和验证等方面进行了评价。在图像检索和聚类方面，我们使用Stanford Online Products[22]、CARS196[19]和CUB200-2011[37]数据集，遵循Song等[22]的实验设置。The Stanford Online Product 数据集包含22,634个类别的120,053幅图像。前11,318个类别用于训练，其余的用于测试。CARS196数据集包含196个模型的16,185张汽车图像。我们使用前98个模型进行训练，其余的用于测试。CUB200-2011数据集包含了200种鸟类的11,788幅图像。前100个物种用于训练，其余的用于测试。

我们基于标准Recall@k度量来评估图像检索质量，像Song et al.[22]一样。给定ground-truth聚类，我们使用NMI分数 去评估聚类对齐的质量。其中I(.,.)和H(.)分别表示互信息和熵。我是用K-means算法进行聚类。

为了验证，我们在最大的公开人脸数据集CASIA-WebFace[40]上训练我们的模型，并在标准的LFW[16]数据集上评估。VGG人脸数据集[23]更大，但是它的许多链接已经过期。CASIA-WebFace数据集包含494,414张10,575个人的图像。LFW数据集由13,233张5,749个人的图像组成。它的验证基准包含6000个验证对，分成10个子集。我们根据剩下的9个split为一个split选择验证阈值。

除特别说明外，我们在所有实验中使用的嵌入尺寸为128，输入图像尺寸为224×224。所有的模型都使用Adam[18]进行训练，人脸验证的批量大小设置为200，Stanford Online Products设置为80，其他实验设置为128。网络体系结构遵循ResNet-50(预激活)[13]。为了加快训练速度，我们在人脸验证实验中使用了一个简化版的ResNet-50。具体来说，我们在5个阶段中分别使用了64、96、192、384、768个过滤器，而不是最初提出的64、256、512、1024、2048个过滤器。我们没有观察到由于更改导致的任何明显的性能下降。采用水平镜像和256×256的随机裁剪进行数据增强。在测试期间，我们使用单一中心裁剪防范。人脸图像由MTCNN[42]进行对齐。当对齐失败时，我们使用中心裁剪。遵循FaceNet[25]，我们使用了α= 0.2，对于基于边际的损失，我们初始化了β⁽⁰⁾=1.2和β^(class)=β^(img)=0。

请注意，以前的一些论文使用了提供的边框，而其他的则没有使用。为了公平地与以前的方法进行比较，我们在原始图像和边界框裁剪的图像上评估我们的方法。对于CARS196数据集，我们将裁剪后的图像缩放到256×256。对于CUB200，我们缩放和填充图像，使其较长的边为256像素，保持长宽比固定。

我们的batch构建遵循FaceNet[25]。我们一个batch中每个类使用m=5个正样本。一个batch中的所有正对都被取样。对于正对中的每一个例子，我们采样一个负对。这确保了正对和负对的数量是平衡的，并且每个示例都属于相同数量的正对和相同数量的负对。

 

 

5.1. Ablation study

我们首先了解损失函数、自适应边际和特定的功能选择的影响。我们专注于Stanford Online Products，因为它是三个图像检索数据集中最大的。注意，图像检索倾向于triplet损失而不是contrastive损失，因为只有相对关系matters。这里所有的模型都是从头开始训练的。由于不同的方法以不同的速度收敛，所有方法都训练了100个epoch，并在它们的最佳epoch而不是在训练结束时报告性能。

我们在我们的距离加权采样方法中对随机抽样和semi-hard negative mining两种采样方法进行比较。对于semi-hard negative mining，对pairwise损失函数的距离下界没有自然选择。因此在本实验中，我们使用0.5的下界来模拟triplet损失的正距离。我们考虑contrastive损失、triplet损失和我们基于margin的损失。所谓随机抽样，是指从所有正对和负对中均匀抽样。由于这样的定义不适用于triplet损失，我们只测试contrastive损失和我们基于margin的损失。

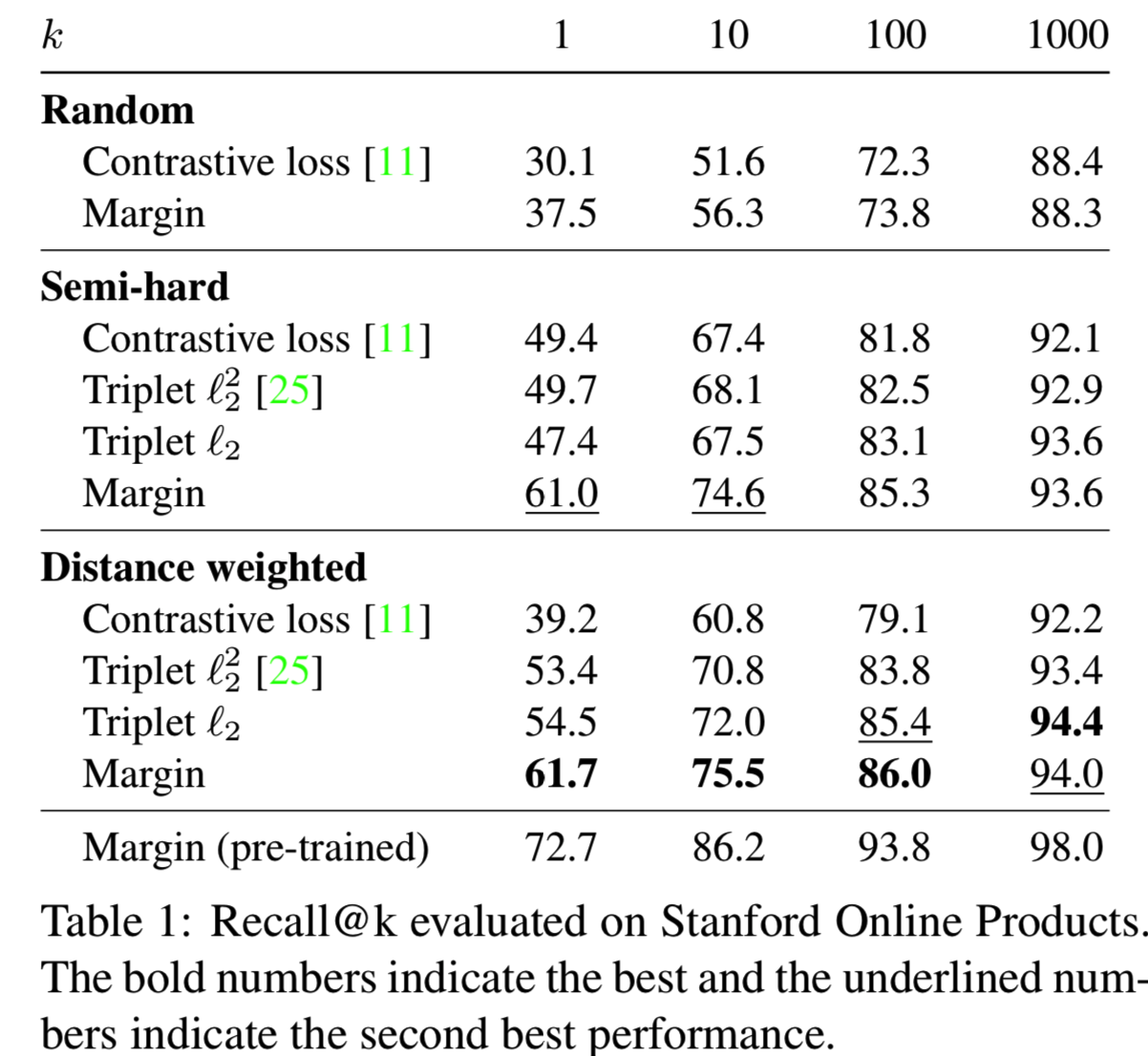
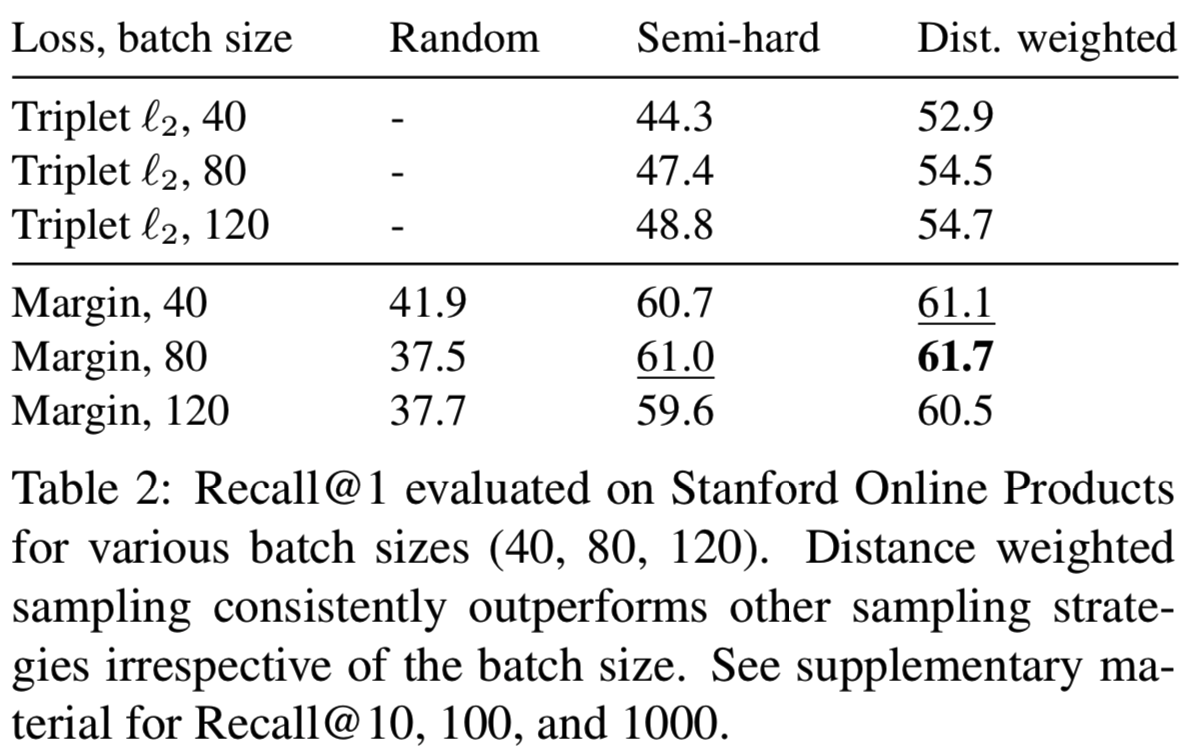
结果如表1所示。我们看到，给定相同的损失函数，不同的抽样分布会导致非常不同的性能。特别地，虽然在随机抽样中，contrastive损失产生的结果比triplet损失的差得多，但当使用类似于triplet损失的抽样程序时，它的性能显著提高。这一证据驳斥了对contrastive损失与triplet损失的常见误解:triplet损失的强度不仅来自损失函数本身，更重要的是来自所伴随的抽样方法。此外，距离加权采样方法始终如一地为几乎所有的损失函数提供了性能提升。唯一的例外是contrastive损失。我们发现它对超参数非常敏感。虽然我们为随机抽样和semi-hard negative mining找到了良好的超参数，但我们还不能为距离加权抽样找到性能良好的超参数。另一方面，基于边际的损失自动学习一个合适的β并很好地进行训练。值得注意的是，不论抽样策略如何，基于边际的损失在很大程度上优于其他损失函数。这些观察结果适用于多个批处理大小，如表2所示。我们还尝试使用ILSVRC 2012-CLS[9]数据集对我们的模型进行预训练，这在之前的工作中很常见[3,22]。预训练可以提高10%的recall。在下面的部分中，我们将重点讨论预先训练好的模型，以便进行公平比较。

 

 

接下来，我们对这些方法进行定性评价。图5显示了对随机选择的查询图像的检索结果。我们可以看到，triplet损失一般能提供合理的结果，但也会出现一些错误。另一方面，我们的方法给出了更准确的结果。

 

通过学习一个灵活边界β去评估所获得的收益，我们比较了使用一个固定β建模和使用可学习的βs建模的效果。结果如表3所示。我们可以看到，使用更灵活的特定类的β^(class)确实比各种固定β⁽⁰⁾值更有优势。我们还使用特定示例的β^(img)进行了测试，但实验没有得出结论。我们推测，学习特定示例的β^(img)可能引入了太多参数，导致过拟合。

 

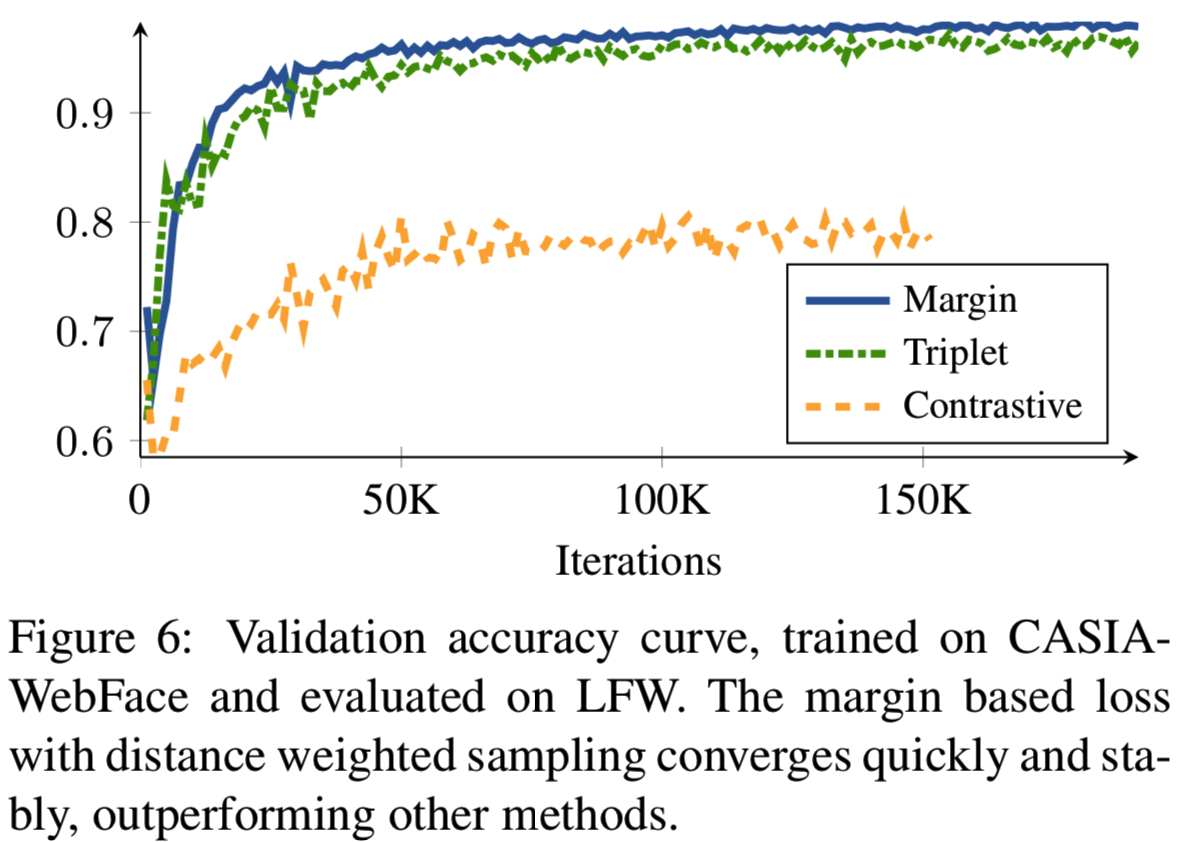
Convergence speed. 进一步分析了采样对收敛速度的影响。我们将我们使用距离加权抽样的基于边际的损失方法与两种最常用的深度嵌入方法相比较:即semi-hard抽样的triplet损失和随机抽样的contrastive损失。学习曲线如图6所示。我们看到，semi-hard negative mining训练的triplet损失收敛速度较慢，因为它忽略了太多的例子。随机抽样的contrastive损失损失收敛得更慢。距离加权抽样使用信息更丰富、更稳定的样本，收敛速度更快、更准确。

Time complexity of sampling 采样的计算代价可以忽略不计。在Tesla P100 GPU上，前向和后向传播每个batch(大小120)大约需要0.55秒。semi-hard采样只需要0.00031秒，距离加权采样只需要0.0043秒，即使在我们的单线程CPU实现中也是如此。两种策略都取O (nm(n−m))，其中n为批大小，m为批中每类图像的数量。

 

 

5.2. Quantitative Results

我们现在将我们的方法与其他最先进的方法进行比较。图像检索和聚类结果见表4、表5、表6。我们可以看到，我们的模型在所有三个数据集中取得了最好的性能。特别是，基于边际的损失优于triplet损失的扩展，如LiftedStruct [22]， StructClustering [29]， N-pair[28]，和PDDM[15]。它的性能也优于histogram损失[34]，后者需要计算相似直方图。还要注意的是，我们的模型只对每个图像使用了一个128维的嵌入。这比HDC[41]更简洁，HDC[41]为每张图像使用3个嵌入向量。

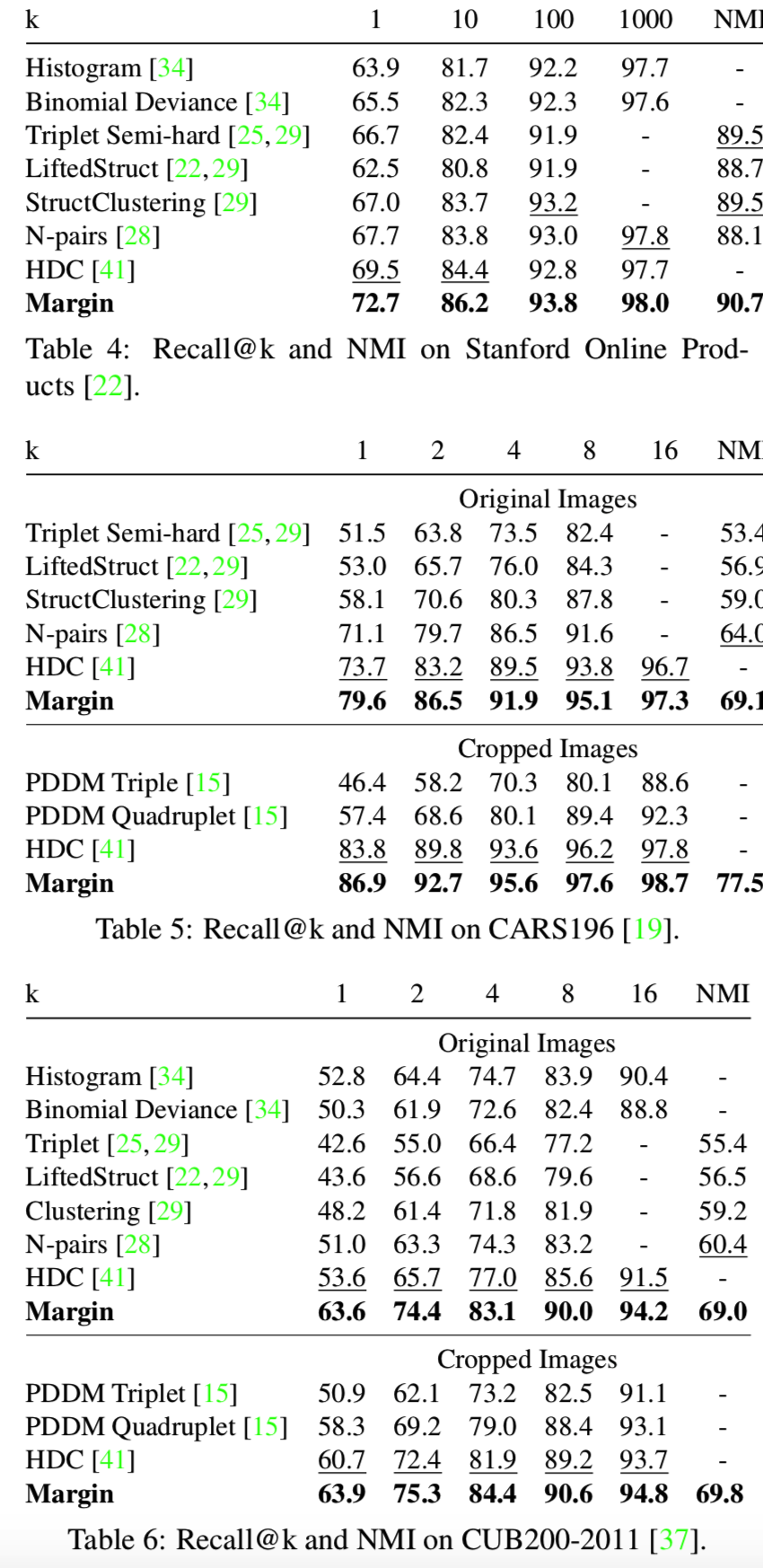
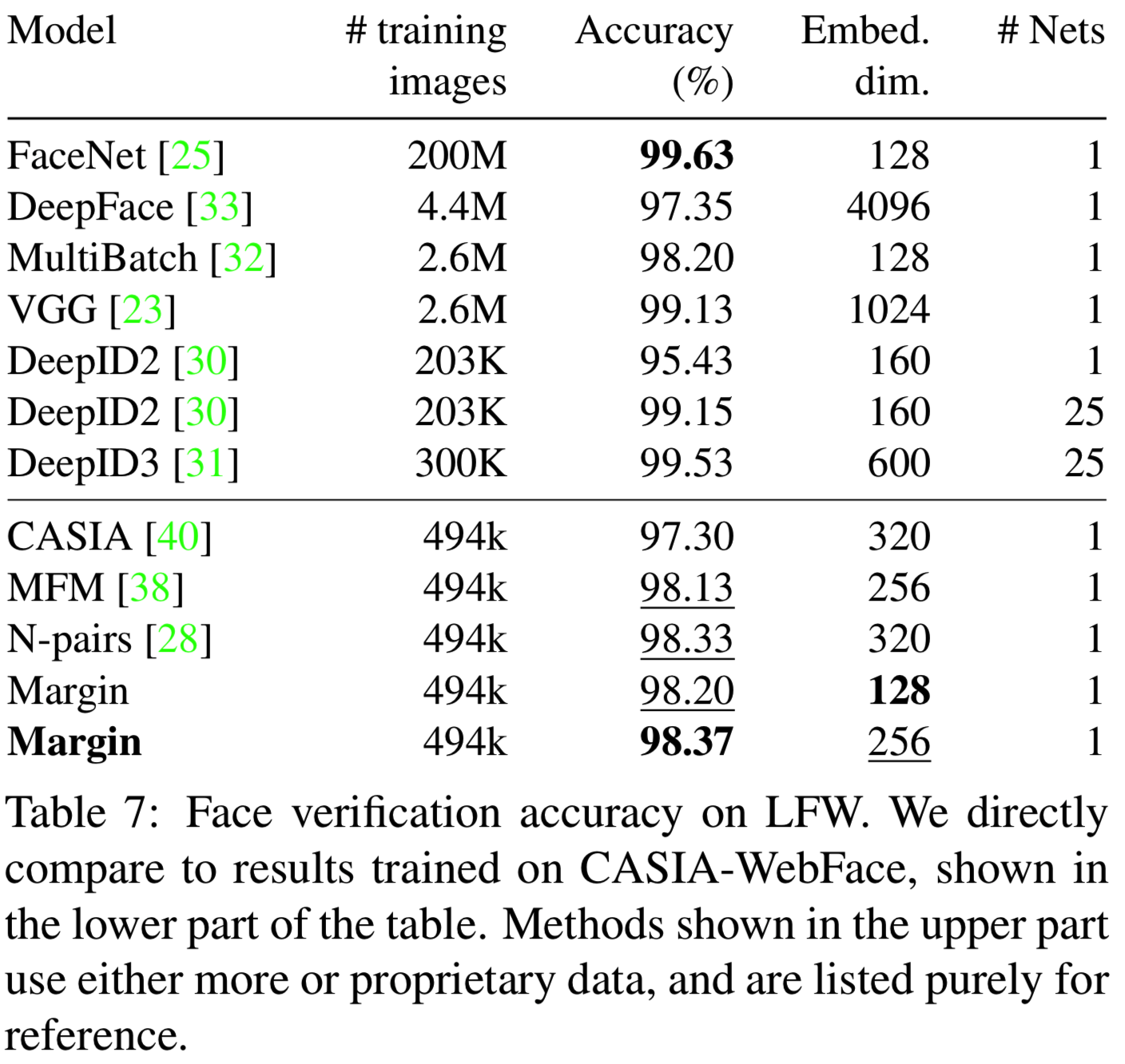
表7给出了人脸验证的结果。在CASIA-WebFace上训练的所有模型中，我们的模型达到了最好的精度。还需要注意的是，在这里我们的方法优于使用广泛训练程序的模型。MFM[38]使用softmax分类损失。CASIA[40]使用softmax损失和contrastive损失的组合。N-pair[28]使用一个更昂贵的损失函数，该函数在批处理中对所有对进行定义。我们还列出了一些其他的先进的结果，他们不能纯粹地作为参考。DeepID2[30]和DeepID3[31]根据人脸landmarks位置在25个人脸区域上使用25个网络。当只使用一个网络进行训练时，它们的性能会显著下降。其他的模型如FaceNet[25]和Deep-Face[33]都是在巨大的私有数据集上训练的。

 

总体而言，我们的模型在所有比较方法中、在所有数据集上都取得了最好的结果。值得注意的是，我们的方法使用了最简单的损失函数——即contrastive损失的一个简单变体。

 

 

6. Conclusion

我们证明了在深度嵌入学习中，抽样比损失函数更重要。这并不奇怪，因为隐式定义的损失函数(相当明显)是一个加权样本对象。

我们的新距离加权抽样方法提高了多个损失函数的性能。此外，我们分析并提供了一个简单的基于边际的损失，它放宽了传统contrastive损失的不必要约束，并享有triplet损失的灵活性。我们表明，距离加权抽样和基于边际损失显着优于所有其他损失函数。

 

代码实现：

class DistanceWeightedSampling(HybridBlock):
    r"""Distance weighted sampling. See "sampling matters in deep embedding learning"
    paper for details.
    Parameters
    ----------
    batch_k : int
        Number of images per class.
    Inputs:
        - **data**: input tensor with shape (batch_size, embed_dim).
        Here we assume the consecutive batch_k examples are of the same class.
        For example, if batch_k = 5, the first 5 examples belong to the same class,
        6th-10th examples belong to another class, etc.
    Outputs:
        - a_indices: indices of anchors.
        - x[a_indices]: sampled anchor embeddings.
        - x[p_indices]: sampled positive embeddings.
        - x[n_indices]: sampled negative embeddings.
        - x: embeddings of the input batch.
    """
    def __init__(self, batch_k, cutoff=0.5, nonzero_loss_cutoff=1.4, **kwargs):
        self.batch_k = batch_k
        self.cutoff = cutoff

        # We sample only from negatives that induce a non-zero loss.
        # These are negatives with a distance < nonzero_loss_cutoff.
        # With a margin-based loss, nonzero_loss_cutoff == margin + beta.
        self.nonzero_loss_cutoff = nonzero_loss_cutoff
        super(DistanceWeightedSampling, self).__init__(**kwargs)

    def hybrid_forward(self, F, x):
        k = self.batch_k
        n, d = x.shape

        distance = get_distance(F, x)
        # Cut off to avoid high variance.
        distance = F.maximum(distance, self.cutoff)

        # Subtract max(log(distance)) for stability.
        log_weights = ((2.0 - float(d)) * F.log(distance)
                       - (float(d - 3) / 2) * F.log(1.0 - 0.25 * (distance ** 2.0)))
        weights = F.exp(log_weights - F.max(log_weights))

        # Sample only negative examples by setting weights of
        # the same-class examples to 0.
        mask = np.ones(weights.shape)
        for i in range(0, n, k):
            mask[i:i+k, i:i+k] = 0

        weights = weights * F.array(mask) * (distance < self.nonzero_loss_cutoff)
        weights = weights / F.sum(weights, axis=1, keepdims=True)

        a_indices = []
        p_indices = []
        n_indices = []

        np_weights = weights.asnumpy() #size is (batch_size * batch_size),即np_weights[2,5]表示选择第6张图作为第3张图负例的权重
        for i in range(n):
            block_idx = i // k

            try:
                n_indices += np.random.choice(n, k-1, p=np_weights[i]).tolist() #即[0:n]这个图以np_weights[i]一一对应的权重采样，取k-1个做负例
            except:
                n_indices += np.random.choice(n, k-1).tolist()
            for j in range(block_idx * k, (block_idx + 1) * k):
                if j != i: #因为每K个batch_k是同一个类，所以当a图为i是，取非i的其他k-1张图作为正例
                    a_indices.append(i)
                    p_indices.append(j)

        return a_indices, x[a_indices], x[p_indices], x[n_indices], x

    def __repr__(self):
        s = '{name}({batch_k})'
        return s.format(name=self.__class__.__name__,
                        **self.__dict__)