图像检索 PCA Whiten - the benefit of PCA and whitening -1 - 论文学习
Negative evidences and co-occurences in image retrieval: the benefit of PCA and whitening
Abstract
提出了一种基于短向量表征的大规模图像检索方法。研究了主成分分析(PCA)降维方法,并对其不同阶段进行了改进。我们展示并明确利用了i)均值减法和negative evidence之间的关系,即,在两个被比较的描述中相互缺失的视觉词,以及ii)轴去相关性和共现现象。最后,我们提出了一种减少量化工件的有效方法,即对多个词汇进行联合降维。提出的技术是简单的,但显著和持续地改善了在压缩图像表征的最佳结果。在图像分类中的补充实验表明,该方法具有普遍的适用性。
1 Introduction
本文主要解决了文献[1-4]中很多论文都考虑到的大规模图像搜索和目标识别问题。更准确地说,该任务包括在大型图像数据库中根据视觉相似性查找与查询图像最相似的图像。大多数论文依赖于bag-of-words(BOW)表征[1,5,2,3]或其衍生物,如[4]。由于计算或内存的限制,这些方法只能在一台机器上搜索几百万张图像。在本文中,我们将主要关注更可扩展的方法,根据最近在压缩图像表征方面的工作[6 - 8],其中图像描述是一个短向量,随后使用二值化[6,9]或产品量化技术[10]对其进行压缩编码。在这种情况下,表现最好的方法是那些从局部特征[7,8]产生代表图像的向量的方法,如Fisher向量[11,12,7]或它的非概率版本,即VLAD描述符[8]。与以更直接的方式从像素[13,6]计算出的全局描述技术相比,这些表示在某种程度上继承了计算它们的局部描述符的不变性属性(视点变化、裁剪等)。
生成短码图像表征的方法通常利用PCA[14]进行降维。观察到,通过PCA reduction,BOW的性能甚至得到了改善。本文对这一现象进行了研究。主成分分析可以看作是一个两步过程(1)以数据为中心,(2)选择一个子空间的去相关(正交)基来最小化降维误差。我们展示了每个步骤对检索都有积极的影响,并且我们提供了对这种行为的解释。在此基础上,我们提出了简单而有效的技术,以进一步提高BOW和VLAD表征的质量。首先,我们考虑negative evidence的作用:给定两个BOW向量,两个向量中jointly missing的一个视觉词在相似性度量中应该得到更重要的信息。我们显示了negative evidence与BOW向量中心(均值减法)的关系。其次,通过利用描述符条目的去相关性,BOW和VLAD表征得到了进一步的改进。提出了两种补充的方法 1)对向量空间进行白化,从而解决了co-currence问题; 2)通过联合降维来考虑多个词汇表。现有技术考虑了多个词汇,例如在层次k-means[2]中,或在[15]的rank聚集技术中。相比之下,我们的方法提高了对描述图像的固定大小的向量的搜索精度。在查询索引结构时,内存和计算复杂度与考虑唯一词汇表时相同。
尽管很简单,但我们在四个流行的基准测试中的结果表明,所提出的技术一致地并显著地改进了基于短向量的最先进的图像搜索。最后,我们将通过在PASCAL VOC'07基准上的实验简要说明,更好的检索表征也能转化为更好的分类结果:我们从BOW获得的短向量,并与线性分类器相结合,显著优于与Chi-square kernel相结合的soft BOW。
本文的结构如下:在第2节介绍了上下文之后,第3节展示了co-missing视觉词的作用,第4节利用白化技术解决了co-currence over-counting的问题。第5节将其扩展到多个词汇表,并与最新的技术进行了比较。
2 Background and datasets
2.1 Image description Framework
Bag-of-words. 作为基准,我们首先考虑由Sivic和Zisserman[1]提出的传统的bag-of-words表征。该表征使用以下步骤从图像中提取全局描述向量。
1. 在图像中检测到感兴趣的协变(covariant)区域[16,17],并由局部d维描述符描述。我们联合使用hessian affine检测器和SIFT描述符[18]。
2. 产生的描述符使用所谓的“视觉词汇(visual words)”来量化,这是通过k-means算法学习产生的“视觉词汇”。
3.使用反文档频率(inverse document frequency,idf)术语计算和加权视觉单词(大小为D = k)的出现直方图。
4. 得到的向量随后被归一化。如[1]中所建议的,我们采用L2归一化。
VLAD. 局部聚合描述符[8]的向量是Fisher向量[11]的简化。这种表征只在步骤3中与BOW有所不同:VLAD不是视觉词出现的直方图,而是在大小为D = k×d 的输出向量中积累描述符与其各自质心的差值。
Power-law normalization. VLAD和Fisher向量表征都是通过使用所谓的power-law normalization[7]改进的[19]。该简单方法后处理了输出图像向量![]()
![]() 。更新后的向量v依次l2归一化。这种后处理的影响被认为减少了多次匹配和视觉爆发的影响。在下面的例子中,我们将会考虑到β=0.5这种变体的存在,即SSR(signed square rooting)。
。更新后的向量v依次l2归一化。这种后处理的影响被认为减少了多次匹配和视觉爆发的影响。在下面的例子中,我们将会考虑到β=0.5这种变体的存在,即SSR(signed square rooting)。
2.2 Efficient PCA
BOW向量和VLAD向量是高维的。例如,BOW的典型值D值在1000到100万个分量之间,而VLAD向量为k×d 维,d为局部描述符的维数。这意味着对于典型参数d = 128和k = 512, D = 65,536。因此,用协方差矩阵法进行主成分分析是无效的,甚至是不可行的。然而,我们只需要方程5中的第一个D’第一特征向量和特征值。通过将学习集Y限制为合理数量的向量(我们使用了在第2节中介绍的学习图像集),我们可以使用dual gram方法(见[14]中第12.1.4段)来学习矩阵P和λ1到λD'的特征值。这相当于计算n×n gram矩阵Y⊤Y而不是D×D 的协方差矩阵C,并利用了这两个矩阵之间特征分解的分析关系。特征值分解使用Arnoldi算法执行,该算法使用迭代程序计算D'个期望特征向量,即那些与最大特征值相关的特征向量。
2.3 Datasets
在文献中广泛使用的一些流行数据集上评估了提出的技术。
Oxford5k[21]和Paris6k[22]: 这些数据集是来自Flickr的图片集合。55个查询对应11个不同的建筑物,由集合中的55幅图像中的边界框给出。任务是检索所有对应的建筑物。性能由[21]中定义的mean average precision(mAP)来衡量。
Holidays(+Flickr1M):此数据集包含INRIA[4]提供的个人假日照片。数据集本身包含1491个图像。500个图像的子集用作查询。每个查询与其他1490个图像以leave-one-out的方式进行比较。为了大规模评估性能,还提供了一个从Flickr下载的100万张图片的干扰数据集。至于Oxford5k,其性能是通过mAP来衡量的。
University of Kentucky benchmark (UKB)。该图像集包含10200幅图像,对应2550个不同的对象和场景(每组4幅图像)。每幅图像都与其他图像进行比较。通常的性能分数是排在前4个位置的图像的平均数量。
对于Oxford5k和Paris数据集,我们使用了在[23]中使用的检测器和描述符,同时在线可用的描述符已用于其他数据集。
Dataset for learning stages: 我们使用独立的数据集(与测试集没有交集)来学习视觉词汇表,以及用于我们技术中涉及的其他学习阶段。在对holiday、Holidays+Flickr1M和UKB进行评估时,独立数据集由Flickr的10000张图片组成。Paris6k用于学习与Oxford5k评估相关的元数据。请注意,idf术语不涉及任何学习阶段,并且是基于索引数据集统计动态应用的。
3 Exploiting evidences from co-missing words
常规的BOW表征只包含非负值,它是作为视觉词出现次数的加权直方图生成的。让我们考虑BOW向量u和v之间相似度s(u, v)的余弦度量,即:
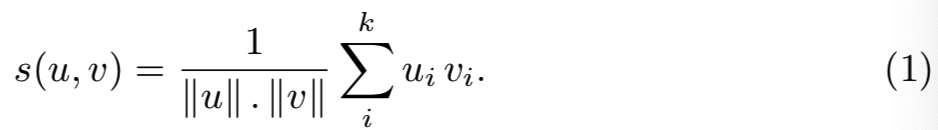
如果ui = 0,则vi等于或大于0时,索引i的视觉词对个体贡献是相同的。这两种情况的差异只被归一化因子||v||所考虑。这低估了零分量的重要性,其为视觉相似性提供了一些有限但重要的证据。
因此,我们提出了一个简单的方法,以在BOW向量中更好地考虑该情况。代替从一开始就测量点u和v之间角度的方法,我们考虑在不同点m处测量得到的两点间的角度。对m来说是mean bag-of-words向量v̄的一部分,即m =α·v̄ 是一个不错的选择。根据式(1)对变换后的向量计算新的余弦相似度,变换后的向量如下计算:
![]()
当α=1时,对应于减去向量均值(从一个学习集产生)。应用这种变换,如果一个特定的视觉词在两幅比较的图像中都不存在(更准确地说,如果它出现的次数少于平均次数),那么余弦相似度就会对它做出正向贡献。因此,单词包之间的相似性得到了改善,如图1所示。
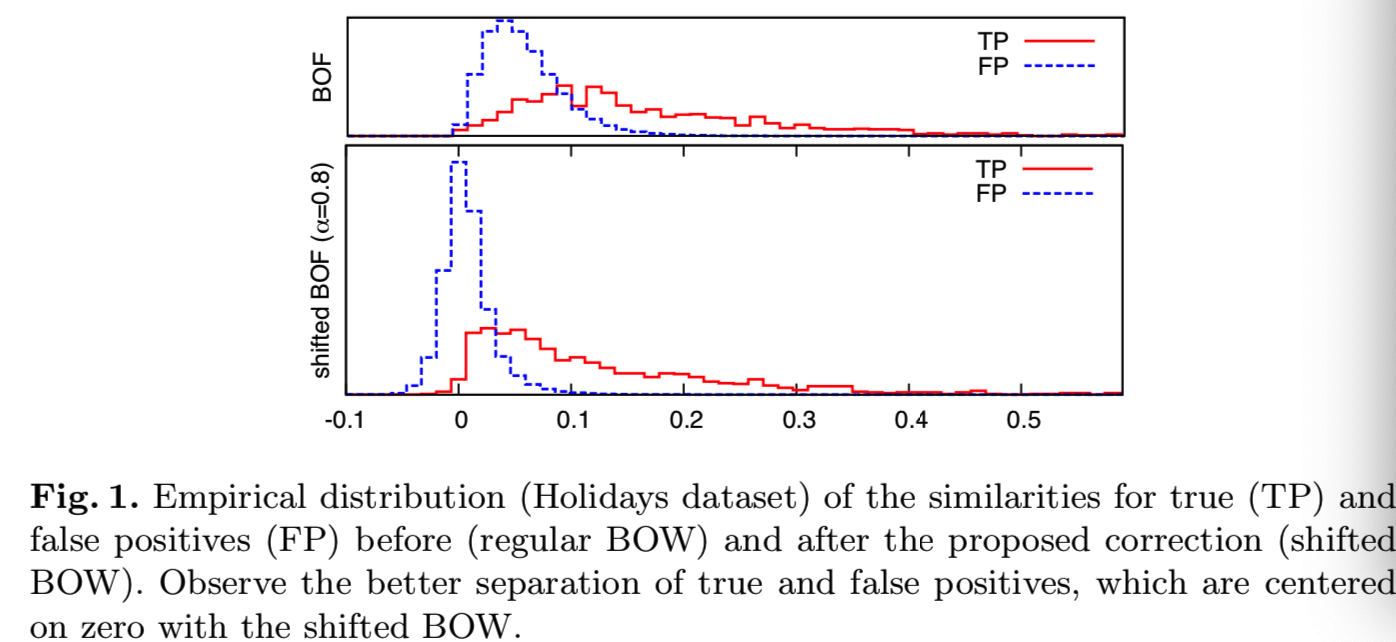
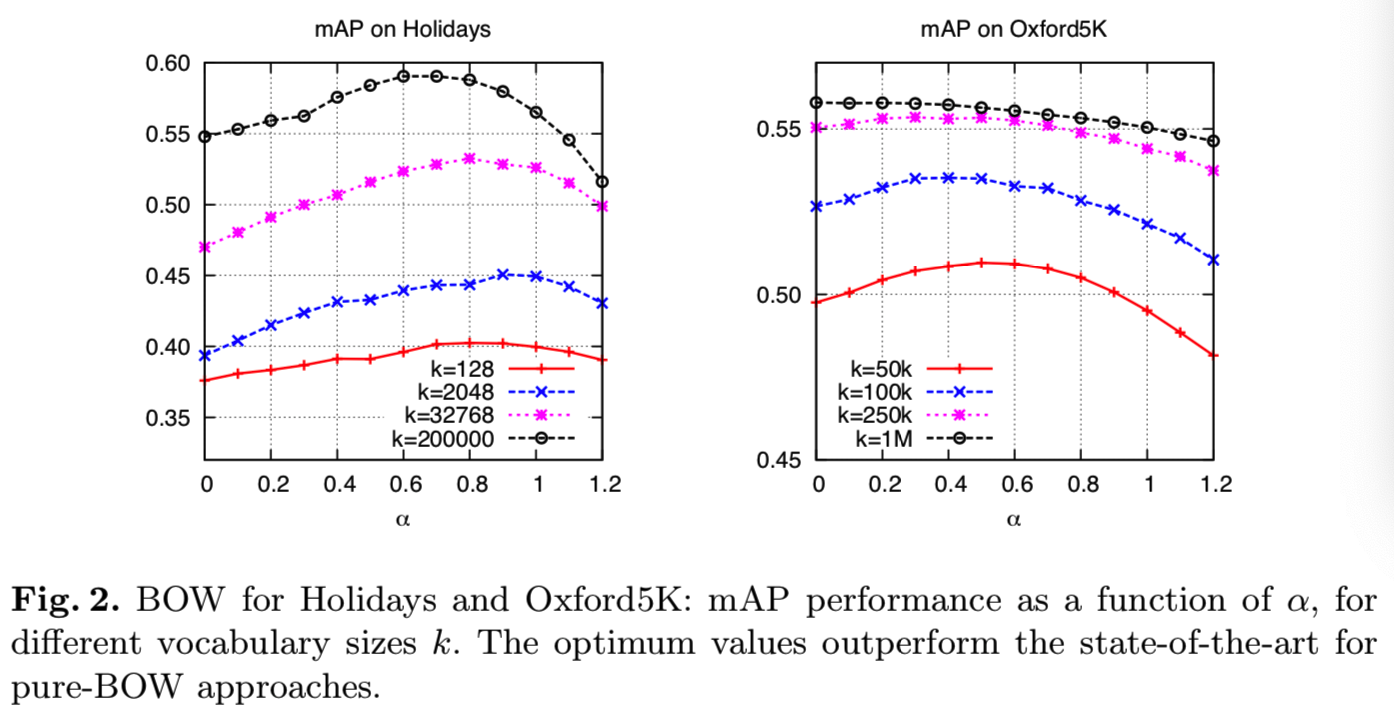
图2显示了在Holidays和Oxford5K基准度量性能时,上面修正的影响,将影响作为一个α的函数。可以看到,建议的更新提供了一些显著的改进,特别是对于更小的词汇表规模来说,而且计算和内存成本可以忽略不计,如下所述。
Integration within the inverted file system. inverted文件结构通过仅评估等式(1)中内积的非负元素来允许稀疏向量有效的余弦距离评估。从数据库中所有稀疏向量中简单地减去非稀疏向量m,会对检索的效率和内存占用量有严重的负面影响。然而,使用与评估(1)相同的inverted文件结构计算新的相似度度量是可能的。相减后的余弦距离表示为:
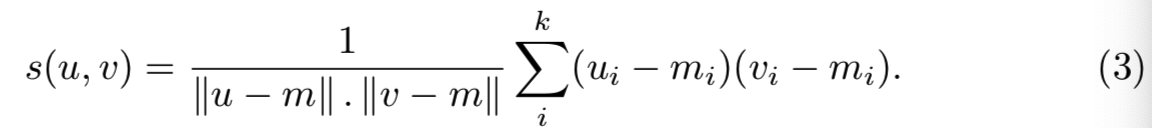
对于数据库中的每个文档v,归一化因子|| v-m ||是独立于查询的,因此能预先计算。因此相似度可重写为:
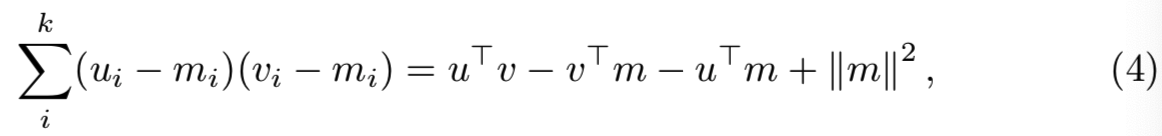
点积u⊤v的有效计算使用如(1)的原始inverted文件结构。v⊤m这个项是独立于查询。因此,它是在向索引中添加BOW向量时计算和存储的。u⊤m这个项仅取决于查询(每个查询计算一次),|| m ||2是一个常数。因此,尽管本文的其余部分主要考虑短向量表示,但我们必须指出,我们的shifting方法在考虑常规inverted文件实现时是有效的[1-3],其内存和计算成本可以忽略不计。
Discussion. 从图2可以看出,negative evidence(即上面减去均值后,原来出现次数为0或小于平均次数的值就会变为负值,这里就称之为negative evidence)对小词汇的影响较大,对大词汇的影响较小。这有一个直观的解释。对于大型(精细)词汇表,co-missing的视觉词成为更常见的事件,携带较少的evidence,而相同的视觉词的存在提供了强有力的证据。对于较小的词汇量,positive evidence和negative evidence的相对权重正在发生变化。这在图2中可以观察到(特别是Oxford 5K数据集的图),图中,随着词汇量的增加,α的最优值(α值越高,negative evidence的权重越大)向左侧移动。
4 Co-occurrence over-counting: the benefit of whitening
利用主成分分析(PCA)直接对BOW (VLAD)向量[8]进行降维是一种获得更短图像向量表示的有效方法。这首先执行了数据的隐式中心化(即减去均值),因此考虑了co-missing的视觉词,从而提高了相似度度量。其次,通过集中第一分量的矢量energy,为降维后的矢量之间的相似性提供了投影前相似度的合理近似。我们采用这种方法从BOW和VLAD表示产生短向量。
但值得注意的是,这种盲目降维忽略了一个重要现象,即co-ocurring问题。Chum等人[24]注意到,在比较两种图像向量表征时,co-ocurring会导致对某些视觉模式的over-count。检测器还可以引入一些人工视觉词的co-ocurring,例如,当一个图像区域从不同的方向[25]被多次描述时,产生两个不同但强烈co-ocurring的描述符。
考虑图像全局描述符(BOW或VLAD)的学习集,根据均值中心化,用矩阵Y = [Y1 | ... | Yn] 表示。D维协方差矩阵被估计为 C = Y×Y⊤。在这个矩阵中捕捉到的co-ocurring的视觉词产生了强烈的对角响应,并倾向于出现一个特征向量与一个包含这些值的大特征值相关联。因此,限制co-ocurring影响的一种有效方法是对数据进行白化,就像[26]独立分量分析中所做的那样,并通过Mahalanobis距离隐式实现。
在我们的例子中,这个whiten操作与从D到D'维的降维操作共同执行: 一个给定的图像描述符X(BOW或VLAD)首先进行PCA投射和截断,然后白化和重归一化得到新向量![]() ,这就是我们的短向量图像表征。该表征如下所示:
,这就是我们的短向量图像表征。该表征如下所示:
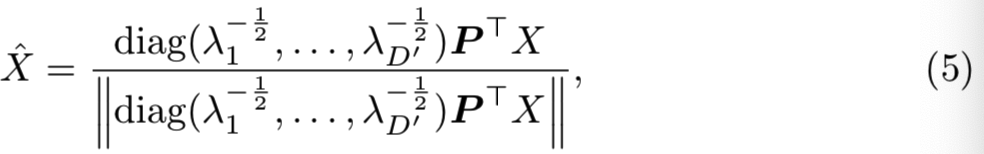
(PCA投射和截断即PTX,白化操作即上面的![]() ),重归一化即
),重归一化即![]() )
)
其中D×D'矩阵P是由协方差矩阵C的最大特征向量组成,其中,λi为第i个最大特征向量所对应的特征值。因此,将降维后得到的两个向量用欧几里得距离进行比较,与使用Mahalanobis距离相似,但不同的是,这些向量被截断并重新归一化。利用余弦相似度对简化后的向量进行比较,可以有效地进行比较。重新归一化的步骤对于得到一个更好的比较度量来说是至关重要的(在Holidays数据集上使用重新归一化将mAP提升了10%)。
Impact on performance. 为了一致性,本文所有实验都将矢量维数降至D' =128维。图3给出了维度降低、SSR组件归一化的影响,以及我们的白化技术的影响,显示了比BOW基线有很大的改进。
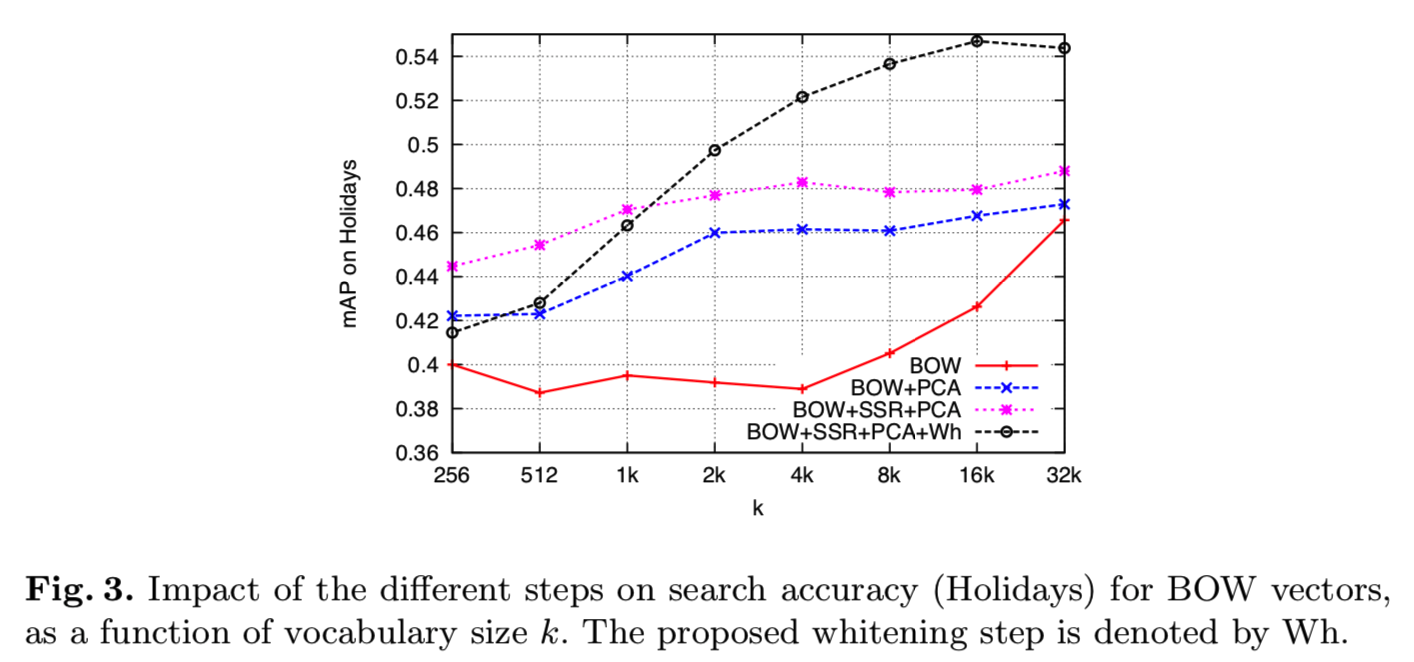
Remarks:
- idf加权项不能在降维的情况下使用,只能在独立数据集上学习。
-作为降维的一个副作用,两个模糊的视觉词i和j在协方差矩阵中比其他元组产生更高的值,这有利于这些视觉词在投影向量中的相同分量的投影。从主成分分析投影重建BOW向量时可以观察到这种现象:另一个视觉词的分量是“幻觉”。
-对于较大的D'值,白化阶段通过放大低energy分量的噪声对性能产生负面影响。这个问题通过使用一种鲁棒的PCA/whiten方法来解决。
5 Joint de-correlation of multiple vocabularies
量化效应对检索质量的影响是众所周知的。针对这一问题,提出了不同的解决方法,包括层次量化[2]、软分配[22]和Hamming嵌入[4]。我们证明了多重 量化可以减轻量化效应。然而,简单的BOW表征的串联不仅线性地增加了内存需求,而且只略微提高了检索结果,见图4或[15]。不同的BOW表征具有很强的相关性。我们证明主成分分析除去了相关性,同时保留了来自不同量化的额外信息。结果超过了短图像表征的最新效果。
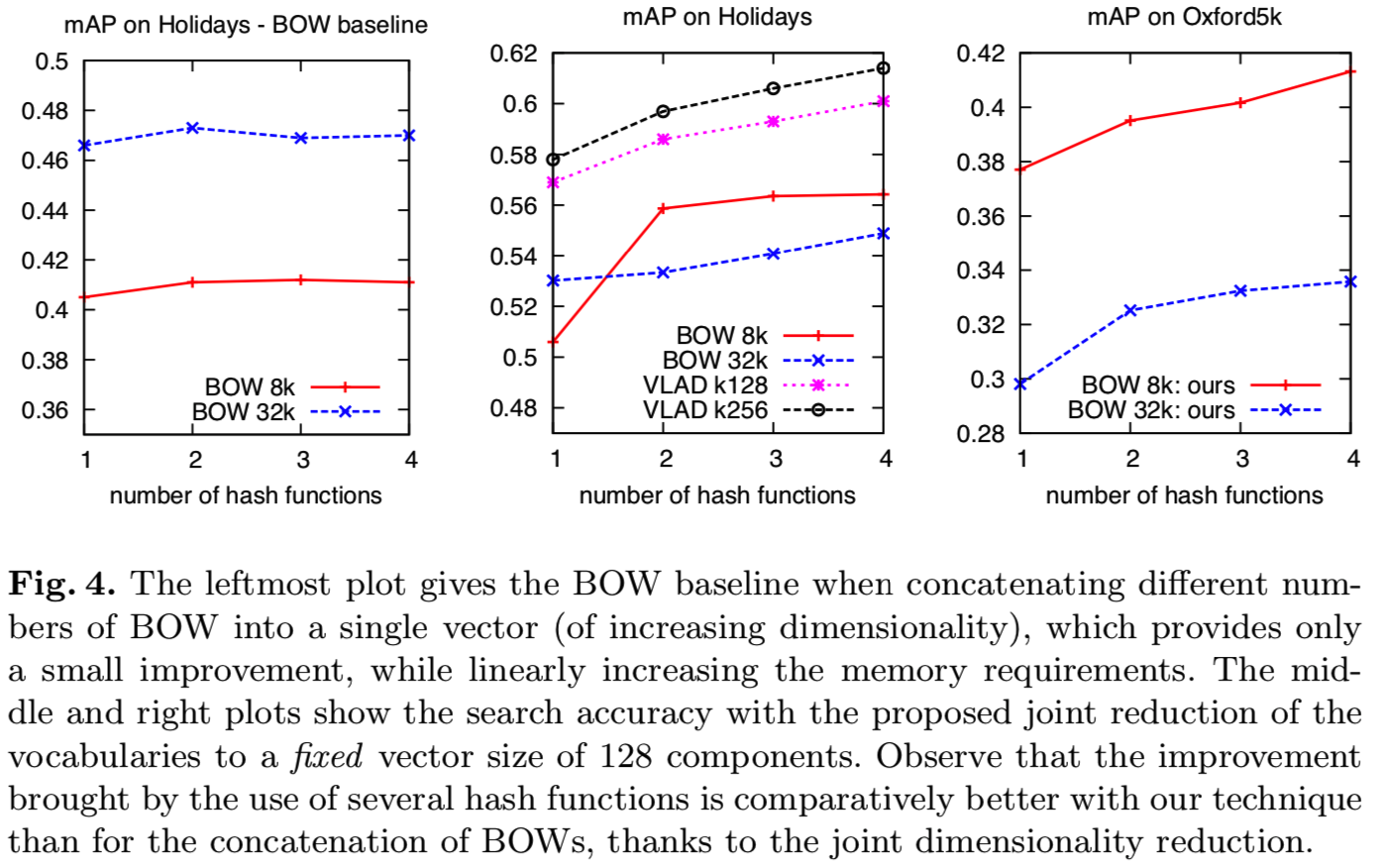
(意思是简单地将多个BOW表征串联的优化效果是有限的,但是如果对多个词汇表进行联合降维到一个固定大小(128),去掉相关的词汇,这时候的BOW表征串联的优化效果更好)
5.1 Related work on multiple vocabularies
一些现有技术提出使用多个词汇表来提高搜索质量,但代价是降低效率和增加内存的使用。例如,一种常见而简单的策略就是简单地考虑将不同的BOW向量串联起来作为图像表征,就像Nister等人[2]所做的那样,他们考虑了一种层次量化方法,其中中间节点对应较小的词汇表。[15]提出了一种基于rank聚集的后期融合技术,但需要并行存储和查询多个inverted文件。此外,这些技术没有考虑词汇表之间的关系:它们的输出被独立处理,而没有考虑量化器之间的依赖关系。
一个更流行的替代方案包括使用multiple[15]或soft[22]分配。当使用inverted文件执行搜索时,这也增加了查询时间。由于我们对大型数据库中的图像搜索更感兴趣,因此,为了在内存中保持索引结构,关注表征的内存大小是至关重要的。
5.2 Joint reduction of multiple vocabularies
多词汇方法的关键是它为不同的词汇执行BOW向量的联合降维,并依次应用前面章节中提到的白化技术去修正由于使用多词汇表导致的artifacts。实际上,不同的词汇表是冗余的:如果两个描述符在一个词汇表中分配给同一个视觉词,那么有很大的概率在另一个词汇表,他们也会被分配给同一个视觉词,从而导致第4小节中提到的那些co-currences。
与[2]和[27]的另一个区别是我们考虑了overlapping量化器。其联合降维,能够比使用multiple或soft量化技术[15、22]的这些方法更好地解决量化artifacts的问题, 通过将使用Fisher向量(soft assignment based on a Gaussian mixture model)或使用VLAD(hard assignment)的多词汇表和单一词汇表比较得到下面展示的结果(表2)。
因此,我们建议对多词汇表进行以下简化:
1.BOW或VLAD向量使用SSR component-wise归一化独立生成(参见第2节)。忽略idf项,因为它的影响在多词汇表中是有限的。应用SSR component-wise的归一化方法,并对串联的矢量进行归一化。
2. 根据第4小节的指导原则,对不同的向量进行联合降维和白化。
图4显示,多词汇表与我们的降维技术一起使用,对BOW和VLAD表示都提供了显著的改进,这对于固定的输出向量D'来说也是如此。BOW使用较大的词汇表并不一定比较小的词汇表好:虽然在Holidays中使用单一词汇表时,k=32k的效果更好,但是我们观察到使用多词汇表的效果会相反。
5.3 Merging vocabularies of different sizes
本小节的目标是解决绝对搜索质量(对于给定的向量大小)和量化代价之间的权衡问题,并提供与文献的类似方法的比较。下面的分析主要针对BOW,因为VLAD通常使用较小的词汇表(例如,k=256)。尽管量化成本并不依赖于数据集的大小,但它会延迟查询(与从图像中提取描述符一起),这对于某些应用程序来说可能非常关键。参考一下,量化一个查询图像的2000个局部描述符成4个词汇,每个词汇包含k = 8,192个质心,使用高效的多线程穷举搜索(exact),在12个核上花费0.45秒。在这种情况下,时间与k成比例。
为了降低量化代价,我们考虑不同大小的词汇表,使用分级k-means方法[2]和 pyramid match kernel [27]方法。不同大小的词汇具有不同的重要性,因此应适应其各自的贡献。我们比较了四种不同的方法来调整词汇的贡献:
1. 所有词汇均采用相同的单位权重。
2. 与[27]类似,词汇表的权重与它的大小(与bins的数量)成比例。
3.我们认为权重与词汇表大小的对数成正比。
4. 与[2]类似,在串联所有词汇表后,权重由idf确定。
在前三种方法(称为“1”、“k”和“log k”)中,每个词汇表的每个描述符首先通过SSR和L2归一化方法进行转换,然后乘以词汇表的权重。将不同词汇表的描述符进行级联,最后对级联后的向量进行L2归一化。在第四种加权方案中,按照[2]中提出的方法,对词汇表拼接后的向量进行idf加权。
表1显示了在考虑多个固定和不同大小的词汇表时的结果,并比较了不同的加权技术。对于固定的量化成本,在本实验中,最佳选择是使用不同大小的词汇表和我们的log加权技术。但是请注意,与所有大小相同的权重相比,后者的改进仅为1%。

5.4 Comparison with the state-of-the-art
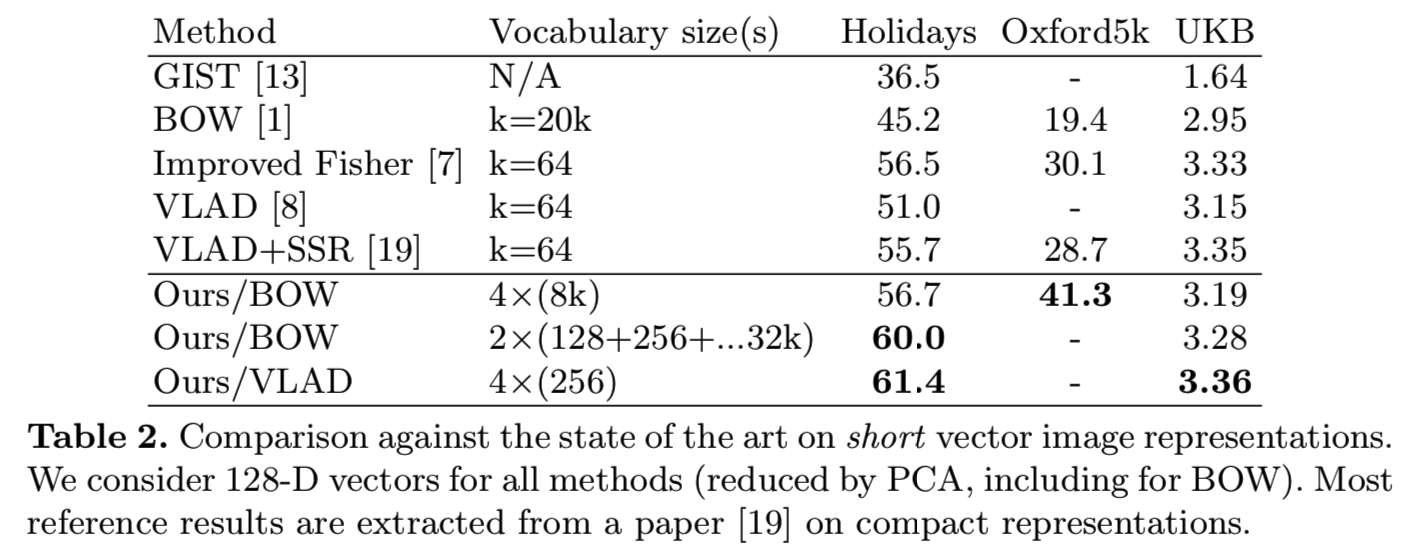
表2将我们的方法与最先进的短向量表征方法相比较。用所提出的短向量构造方法得到的结果始终优于参考结果。当我们的方法应用于BOW时比应用于VLAD时得到了更高的改进。与将20k个centroids的BOW缩减为128维[19]相比,我们的方法在使用4个大小为8k的词汇量的BOW时,Holidays的mAP增加了14.8%,Oxford5k的mAP增加了21.9%。UKB的分数是3.19/4 (BOW reference:2.95)。因此,基于BOW的表征法与PCA-reduced的VLAD和Fisher表征法的最佳结果相比具有竞争力,而在[19]中,这些表征法的表现明显优于BOW。通过将我们的方法应用到VLAD表征上,我们仍然获得了比现有水平提高5.7%的效果。对UKB的改进并不显著。
5.5 Encoding our short vectors with compact codes
使用压缩域近似近邻搜索技术[10]对向量进行进一步编码时,向量越短得到的结果越好,如表3所示。使用16字节的代码,我们在Holidays中将BOW基线的mAP增加了3.6%。在Holidays中使用VLAD(4×k=256),我们的表现比最先进的Fisher向量[19]的mAP好2.5%。

5.6 Large scale experiments
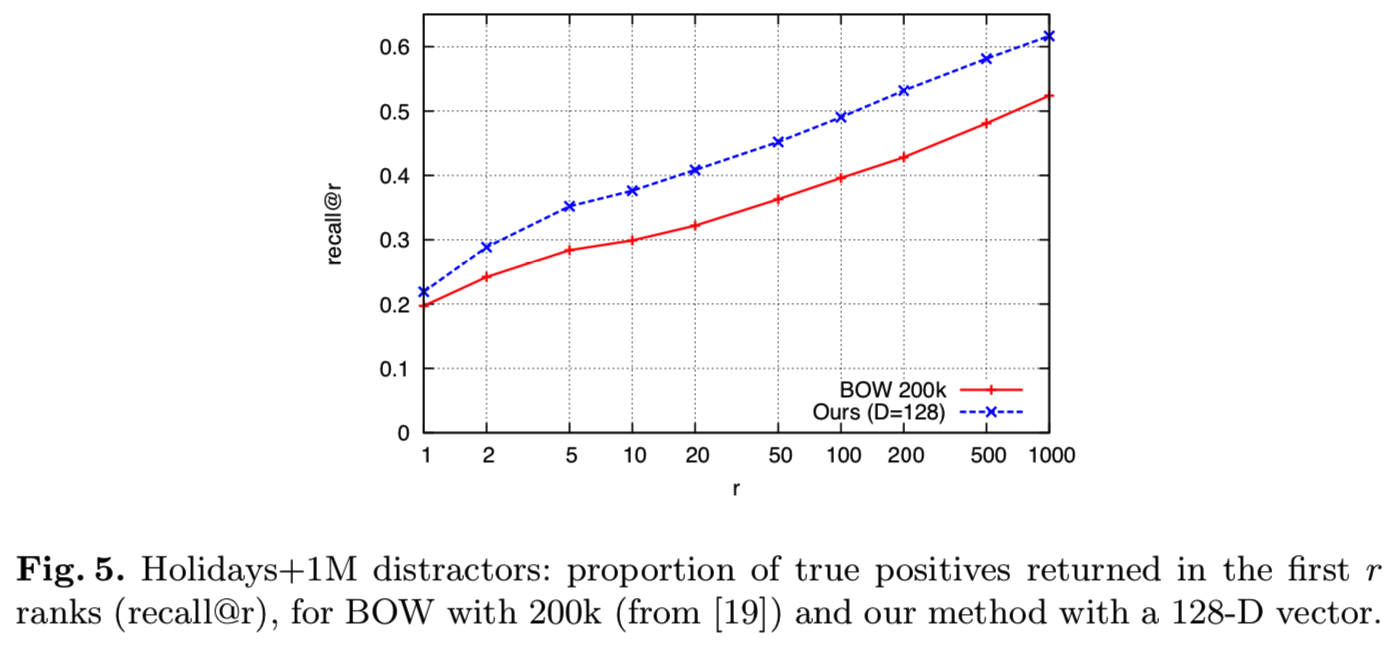
通过合并Holidays数据集和Flickr1M干扰集,我们已经对100万幅图像评估了我们的方法,如[4,8]中所做的那样。我们的方与BOW(k=200k)表征相比较(从[19]的曲线)。
结果如图5所示。我们的方法显著优于基线,这是通过使用仅为128维向量的图像表征来实现的,也就是说,使用的内存比sparse BOW要少得多,后者通常每个编码的局部描述符需要4字节。效率也比BOW好得多。通过穷举搜索的有效实现,使用一台3Ghz机器的12核查询Holidays的全部500个查询图像需要3.08秒,这相当于每次查询要6毫秒。这比BOW[4]报告的时间要快两个数量级。
5.7 Improving BOW for classification
虽然本文的主要目标是考虑使用短向量进行大规模的图像检索,但我们报告了一些初步结果,显示了我们的方法在使用非常短的向量和高效的线性分类器进行分类的情况下的效果。为此,我们使用我们的方法(SSR, 白化4个词汇的联合去相关)对BOW基线进行了改进,并与结合线性分类器的方法进行了比较。在Pascal VOC'07[28]上,在与[29]相同的协议下,我们的技术明显优于相应的BOW:在D'=256维情况下,我们得到的mAP=46.9%,而在4k维情况下,BOW得到的mAP= 41.4%。与采用线性分类器的空间金字塔匹配(SPM,[30])的结果基本一致,但其矢量比线性分类器短100倍。
6 Conclusion
针对大尺度图像检索中的PCA降维问题,提出了不同的改进方法。首先,提出了一个解决方案,给予联合non-curring的视觉词更多的重要性,以微不足道的内存和计算复杂度代价来提高bag-of-words的图像搜索质量。这种方法也可以集成到一个inverted文件中。然后,我们考虑了co-occurring和相关视觉词的问题,以及降维和多词汇的使用。这种方法产生的短向量(128维,即单个SIFT局部描述符的大小)具有很高的检索精度,我们在流行的图像搜索基准上的结果证明了这一点。最后,在图像分类方面表明了该方法的通用性。



