图像检索(image retrieval)- 10相关 - From Single Image Query to Detailed 3D Reconstruction -1-论文学习
这个论文是将当我们手上有一堆数据的时候(如网络数据),先使用image retrieval方法检索出与查询图像相关的图像,即各个大小、方向、角度不同的同一对象的图像,然后就能够使用这些数据作为sfm的输入来实现3D重建了。其实就是将image retrieval与sfm相结合,使效果更好
From Single Image Query to Detailed 3D Reconstruction
Abstract
在过去的十年中,对无序图像集合的Structure-from-Motion已经在规模上取得了显著的进展。这一令人印象深刻的进展部分归因于为这些系统引入了有效的检索方法。虽然这提高了可扩展性,但也限制了大规模重建系统能够生成的细节量。在本文中,我们提出了一种联合重建和检索系统,该系统在保持大规模Structure-from-Motion系统的可扩展性的同时,也恢复了经常丢失的重建场景细节的能力。我们在从互联网上下载的740万幅图像的大规模数据集上演示了我们提出的方法。
1. Introduction
近十年来,计算机视觉在图像检索和三维建模方面取得了很大进展。当前的图像搜索引擎都是基于web规模的图像集合,能够定位特定的对象和landmarks,并帮助用户友好的内容浏览。在从图像和视频中重建场景的领域中,从无序的互联网照片集合中进行三维建模可以说是迈出了最大的一步。一个自然的进步是解决了在一个单一的、用户提供的照片中描述的对象上获得一个对象的详细3D模型。
Structure-from-Motion (SfM) 系统已经从 从几千张图片[29,30]中建模场景扩展到从数百万张城市规模的图片集合[7,9]中建模。早期的照片采集重建系统利用图像对的穷举匹配来确定可能的重叠图像对。这通常是图像和特征数量的平方。因此,该方法不具有扩展性(即不适用于数量很大的数据集),不适用于通常可获得的包含数千甚至数百万幅图像的数据集。然而,穷举匹配保证了发现所有可能的相机重叠。为了实现可扩展性,目前最先进的大规模重建系统放弃了穷举的两两重叠确定方法。相反,现代系统利用图像检索算法[21,3,4]或图像聚类技术在重建过程中识别重叠图像(即寻找相似图像),如Agarwal等人[1]和Frahm等人[7]的系统所证明的那样。虽然图像检索的引入对于提高重建方法在大数据集上的可扩展性至关重要,但它也严重影响了重建场景细节的能力。这个问题的根源是显示细节的图像对在检索结果中经常缺失。这是不理想的,对于Zhang等[36]最近提出的使用无序的照片集合进行照片视野扩展的应用,最好在重建时提供细节。
缺乏细节是采用的检索方法[21,3,4]的结果,这些方法经过调整,以获得在尺度和外观上相似的图像。本文介绍了一种用于大规模重建的紧耦合检索和SfM系统,使用的是数百万张图片的无序照片集合,该系统不仅恢复了场景的粗糙几何,而且特别关注了场景细节的建模。我们的方法通过在不同规模的场景图像上结合SfM和检索来实现这一点。
为了实现这些细节重建,我们的系统必须克服以下挑战:
- 实现概览(overview)图像和详细(detailed)图像的更平衡检索,为精细细节重建提供所需的图像。
- 克服概览(overview)图像和详细(detailed)图像之间的大分辨率差异导致的配准(registration)不确定性。
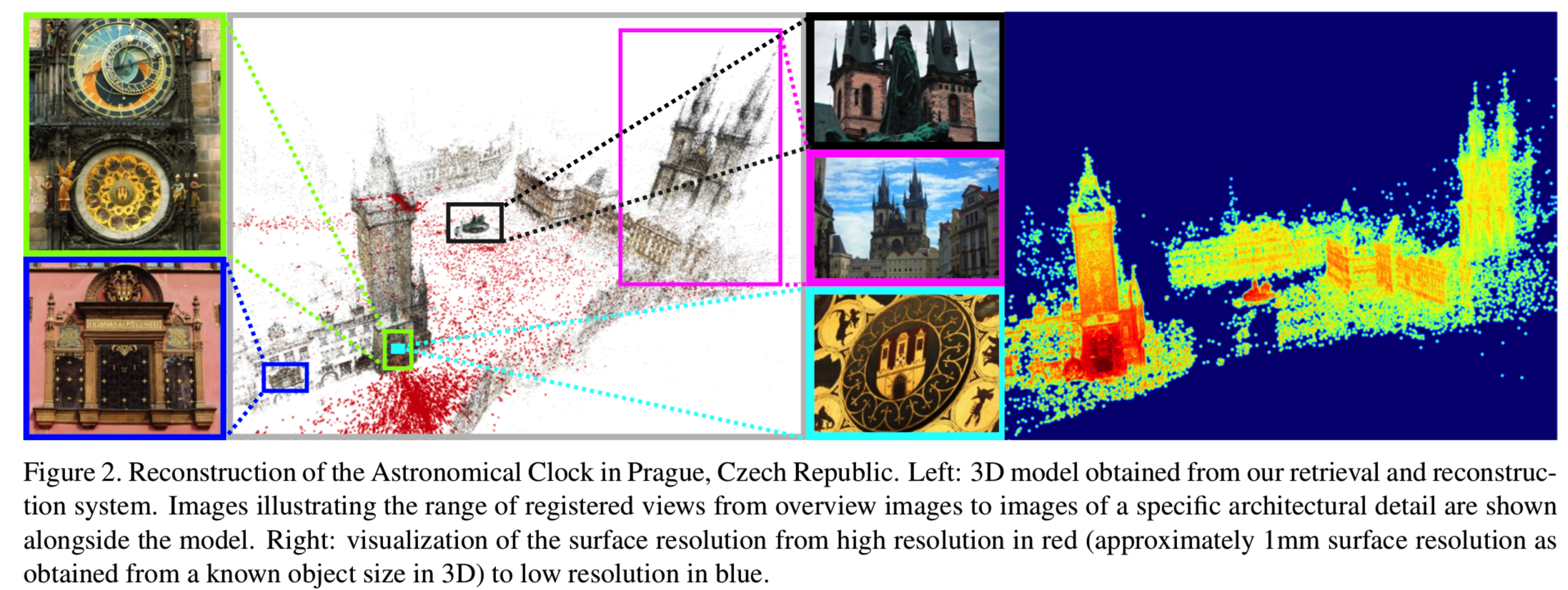
我们提出了一种紧密耦合的SfM和检索系统来解决这些挑战。基于当前最先进的三维重建技术,在重建系统和检索系统之间建立交互链接,使我们能够控制检索特性。这允许我们专门检索克服SfM挑战所需的图像。我们从无序的互联网照片集合中得到的重建结果显示了好的几何细节,同时传达了整个场景的结构。图2显示了一个重构示例。
2. Related work
我们的系统同时利用检索和SfM算法来实现详细场景重建的目标。在本节中,我们将讨论这两个领域中相关的最新技术,然后在接下来的部分中更详细地介绍我们的方法。
在过去的十年中,通过用户定义图像查询来研究大规模无序图像集合——大规模图像检索问题——取得了显著的进展。大多数方法将问题视为描述符空间中的最近邻搜索,如bag-of-words[28,21,25,11],VLAD [12, 2], Fischer vectors[24],或穷举匹配(exhaustive matching)[34,27]。最近,Mikulik等人[18]指出,最近邻图像搜索对于用户来说不是最优的,用户通常是在寻找新的图像信息,而不是接近重复的图像。在[18]和[19]中分别提出了用于规模极端变化和细节图像挖掘的新公式和有效方法。我们将这些想法扩展到识别适合于三维重建的初始图像集,然后利用获得的重建结果提出进一步的图像检索目标。不是针对对人类用户有吸引力的极端规模变化,而是采样整个规模变化谱,这更适合于三维重建。在此基础上,我们提出了一种有效的基于内容的landmark爬行检索方法,挖掘连接landmark多个侧面的视图。
Snavely等人的开创性论文[29,30]介绍了从互联网照片集进行场景重建。这是第一个表明SfM可以用于数千个图像的这种不同的、无序的集合的方法。该重建系统的主要局限性是由于穷举图像对重叠评估,其可扩展性有限(即对图像的数量规模有限制)。
为了克服可扩展性的不足,Li等人[13]引入了基于外观的聚类来对图像进行分组。这使得在一台PC上从成千上万的图像建模成为可能。Agarwal等人[1]引入了一种云计算算法,可以在24小时内在62台计算机上对15万幅图像进行建模。该方法利用基于查询扩展[4]的词汇表树搜索来确定重叠图像,然后进行近似的最近邻特征匹配。虽然提供了可扩展性,但这种方法严重损害了用于配准和重建的细节图像的检索。Lou等人[15]提出了一种改进的基于词汇树的检索方法,增强了检索结果的多样性。提出的重加权方法提高了SfM重建的场景覆盖率,但并没有解决不能提取细节图像的问题。
Frahm等[7,1]将Li等人的[13]方法扩展到可扩展到数百万张图像的重建中。然而,这种方法也受到了识别方法——基于gist-feature[22]的外观分组方法——的影响,这些方法无法获得详细的图像,因此严重限制了生成精细细节重建的能力。
Crandall等人[5]提出了一种基于MRF优化的全局SfM方法。为了正确地初始化这种混合优化,他们的方法需要对图像进行近似的地理位置先验。虽然这种方法可以检索地理定位的细节图像,但互联网上的照片集合中有很大一部分不是地理定位的。因此,这种方法在我们的场景中限制非常大,与我们的方法相比,它只能register一小部分图像。
3. Overview
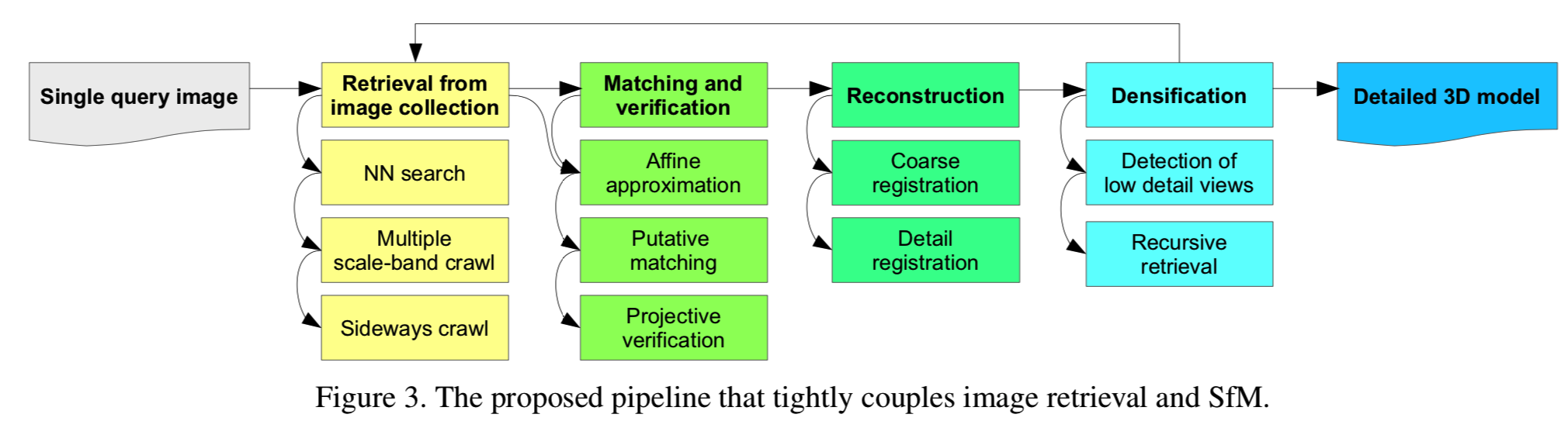
我们提议的pipeline(图3)处理数百万个无序图像大小的图像采集。一个用户提供的查询图像作为该pipeline的输入。在第一阶段,以查询图像作为图像检索的初始种子(第4节),检索阶段首先查找最邻近的图像,然后进行multiple scale-band crawl,以获得不同zoom级别的附加视图(第4.1节)。此外,我们通过检索查询图像的左边和右边的图像来扩展查询,以获得查询图像周围的附加上下文信息(第4.2节)。作为后续重建阶段的准备,我们提出了一种高效的匹配方法(第5节),利用检索阶段的副产物来智能地避免不重叠的图像对。在重建阶段,我们使用了几种方法来克服细节图像配准的困难(第6节)。最后,我们通过识别模型的低细节部分,并递归地检索额外的图像进行另一轮重建,来进行额外的densification(第7节)。在对数以百万计的图像数据集进行的综合实验(第9节)中,我们证明了该方法可以产生大规模、高质量的模型,并且能够捕捉场景的细节。
4. Image retrieval
3D重建中检索的目的是提供一个有着多种视点(用于重建的稳定性)的匹配图,图像序列在极端视点或尺度变化(能够连接不同部分并帮助消除歧义复制结构)之间的提供了一个平滑的过渡,和对在空间和尺度(扩展重建和改进的详细级别)中的进一步结构的图像进行挖掘。
检索引擎建立在具有快速空间验证[25]的bag-of-words表示之上。Hessian仿射特征[17]被旋转变式[23]SIFT描述子[16]检测(平均每张图像1900个特征)和描述。使用有着近似近邻搜索[20]的k-means方法,描述符被向量化成1600万个visual words。然后使用快速空间验证[25](每秒几百个图像对)估计查询图像和结果图像之间的近似仿射变换。为了加强变换的一致性(尺度变化、转换),每个特征的尺度和位置信息都包含在反向文件中[11,31]。
该方法以查询图像为入口点,从图像集合中获得初始匹配图。根据预期的结果(查询图像中可见场景的详细重建,或查询图像的整个邻域的详细重建),使用不同的挖掘技术来生成初始匹配图。一旦(部分)重构可用,同样的技术应用于增量地扩展重构;见第7节。
4.1. Multiple scale-bands
为了检索不同细节级别(和/或不同程度的上下文)的相关图像,我们构建了分级查询扩展[19]的方法。与[19]不同的是,我们对极端的尺度变化不感兴趣,而是对捕获一个平滑的尺度过渡的图像序列感兴趣,以支持稳定的SfM估计。
分层查询展开的过程如下。随查询图像发出一个鼓励尺度变化的初始查询。为了反映图像排名中的比例变化,我们使用document at a time(DAAT) scoring[31],去利用存储在一个反向文件中的几何图形。这个初始查询的结果在规模空间中聚集。然后使用每个空间图像集群发出一个新的扩展查询[4],该查询检索给定位置的进一步详细信息。图4显示了四个尺度波段——context(zoom out)、原始尺度、两个中级细节的例子(zoom in),以及每个中级波段的三个详细图像。

4.2. Sideways crawl
从单个查询图像开始检索多个尺度波段的图像,将得到图像尺度的整个频谱,但通常只从单个查看方向进行检索。然而,许多有趣的场景部分往往位于角落或观察地标的旁边。在这种情况下,为了获得更加完整和稳定的模型,在地标周围额外的sideways crawling对重建有显著的好处。crawling是在原始查询图像的左侧或右侧执行的。我们提出了一种新的,有效的检索方法,基于内容在视点的周围crawling。因此,我们成功地挖掘出了连接地标多个侧面的图像(见图5),或者是在室内情况下,得到整个感兴趣区域的视野更广的图像(见图4)。

sideways crawling检索包括两个阶段。第一阶段允许我们在不同的方向(左和右)crawl图像。在第二阶段,最初的检索集合被来自期望方向的附加图像扩展。
第一阶段利用查询图像和结果之间的估计几何变换(在我们的例子中是仿射变换)。例如,在向右移动时,查询图像右侧的特性应该与结果图像左侧足够多的特性匹配。这可以通过对候选结果进行几何重新排序或更有效地使用DAAT方法[31]来实现。附加的几何分析,如通过homography拟合估计水平消失点的位置,这可以在额外的计算工作中执行。
为了检索包含新图像信息的更大一组相关图像,将使用第一阶段中排名最高的图像执行附加查询。在这些扩展的查询中,只考虑原始查询图像中不可见区域的特征。最后,将检索到的图像合并,然后根据视点变化的数量重新排列。
为了从各个方向重建地标,将重复sideways crawling,如图5所示。为了重建地标的各个侧面的细节,每一步都要进行多尺度波段的挖掘。有关sideways crawling的进一步例子,请参阅中国兵马俑地标的室内视图(图4)。在介绍了图像检索系统之后,我们接下来详细介绍利用建议的检索系统的独特特性的SfM系统。
(其实就是使用image retrieval方法先将相似图像检索出来,然后就能够应用这些与查询图像相似的图像到sfm中)
5. Matching and geometric verification
最先进的SfM系统[7,1]已经在城市规模的重建上取得了令人印象深刻的效果。传统图像检索的特点是缺乏细节重建的一个常见原因。也就是说,当从场景的概览图像开始时,场景的细节图像不会被作为最近邻来检索,这是因为两者低重叠或大量相似的视图排名超过了细节图像[19]。在SfM中不配准(registering)检索到的细节图像的原因是,SfM通常需要在细节视图区域中具有高表面分辨率的细节视图和具有相对较低表面分辨率的概览图像之间建立连接的过渡图像。在本文中,我们提出了一种新的结合面向细节的检索和SfM系统的方法,以解决从无序的照片集合中获得三维模型的挑战,该模型能够提供完整的场景覆盖和场景细节的高几何分辨率。
与传统的基于词汇和聚类的图像检索方法相比,本文提出的图像检索方法具有很大的优势。由于该方法在检索过程中通过仿射变换估计来进行空间验证,因此在检索初期就能得到场景重叠的定量测度。inliers数作为相似度评分,是RANSAC[6]鲁棒估计的副产物。
接下来,在SfM中对图像对的几何验证,即对偶极几何(epipolar geometry)的检验,在投射空间中操作,估计移动摄像机的基本矩阵和纯旋转摄像机的单应性。因为仿射变换空间是一个投影转换空间的子空间,我们可以使用correspondences集合之间的一个仿射变换(affine transformation)的存在作为一个代理来假设相同的图像对之间的correspondences集合的一个投射变换(projective transformation)的存在。虽然,在理论上,投射变换可能不能行使所有的自由度,但在实践中遇到这些配置的机会是非常低的。事实上,在实验数据集中有超过99.9%的图像对(第9节),当存在仿射变换时,我们可以估计出一个有效的正极几何或单应性。因此,如果我们强制仿射变换的存在,SfM的几何验证只需要处理有效的图像对来重建。这就避免了由于不重叠对而造成的巨大开销(即删去了那些和查询图像不相似,即不重叠的图像)。这使得用于几何验证的RANSAC速度显著加快,因为RANSAC在模型参数数量和测量值的outlier ratio方面具有指数级的计算复杂度。
利用检索系统提供的早期相似性度量,可以显著提高SfM估计的性能和可靠性。这是因为我们提出的管道可以根据仿射变换inliers的数量对检索到的图像进行排序,而后续的几何验证只需要在重叠的图像对上花费时间。这使得我们只能匹配有限数量的图像,而不是像传统的基于词汇表树的方法那样匹配更大的最近邻集。在所有的实验中,我们都试图在最大数量为200幅的检索图像中验证一幅查询图像,我们通过实验发现,对查询图像具有至少8个仿射变换inliers的最近邻图像有很高的成功配准的可能性。接下来,我们描述对SfM算法的增强,以可靠地获得几何场景细节的重建。
6. Reconstruction of Details
详细的场景重建依赖于准确和可靠的相机配准,这对于照片集中最高分辨率的图像尤其具有挑战性。主要有三个原因:递增的SfM依赖于相机配准的顺序,在配准详细视图时减少的冗余测量,以及这些视图经常具有挑战性的几何配置。在下面,我们将研究这些挑战并描述我们的解决方案。
一般来说,SfM结果的质量取决于三个主要因素:第一,获得可靠和精确的估计,参数不应该依赖只是一组最小或小的测量去实现测量噪声的补偿(详细视图通常会显著降低与其他图片的correspondences)。其次,可靠性为我们提供了检测outliers的能力,并决定未检测到的outliers对我们估计的影响程度(由于冗余减少,对详细视图的outliers检测具有挑战性)。第三,测量值的不确定性传播到了估计参数的不确定性,观测的几何形状影响估计的稳定性(非常倾斜或远的视图通常测量值明显较高,因此配准不确定度也明显较高)。
首先,由于bundle-adjustment的非线性特性,增量SfM严重依赖于相机配准的顺序。这种效果对于细节场景的重建尤其重要,因为不同层次的细节通常只是稀疏地连接或与前向运动视图连接。由不稳定的观察几何造成,前向运动对sfm来说是一个特别具有挑战性的情况。根据我们的经验,在重建中植入一个详细视图,然后逐步增加模型以包含较少详细的视图,在大多数情况下都是失败的,或者导致模型质量低下。因此,我们变成在重建中植入可以看到一个最大部分的场景的图像,其有效地排除了细节和极度缩小的视图。在此基础上,我们逐步扩展模型,通过根据当前可见场景结构的数量对相机进行配准,避免了尺度的和视点的突然变化。
其次,我们讨论了减少冗余的影响,这是观察场景细节的图像(就是只包含场景的一小部分)经常遇见的情况。由于细节结构的图像只能看到场景的一小部分,因此观察到相同特征的图像通常要少得多。在这种情况下,传统的最近邻匹配产生更少和更短的追踪,因为它不能从已经很小的具有相同结构的图像集合中匹配相当一部分图像对。因此,bundle-adjustment必须处理一个显著减少的冗余测量,其导致不准确和不可靠的相机切除和结构估计。因此在bundle-adjustment(或更一般地,在最大似然估计)的可靠性中,冗余被确定为独立观测数量减去有效自由度[32]的差。因此,我们有两个机会来改善冗余:增加观测的数量和减少自由度。所采用的检索系统本质上减轻了减少冗余的影响,因为它显著地揭示了更多重叠的图像对。通过这种方式,我们能够比以前构建更多、更长的追踪,这导致与标准检索系统(如基于词汇表树的方法)相比,度量的冗余显著增加。此外,我们将我们自己限制在一个相对简单的相机模型,总共8个自由度(3个方向,3个平移,1个焦距,1个一阶多项式radial distortion参数,主点固定在图像中心)。
第三,SfM方法面临着场景和/或相机的困难的几何配置的独特挑战。许多场景的几何细节图像是在高变焦水平,即大焦距下拍摄的。在这种情况下,观察光线接近平行,导致沿观察方向的配准不确定度很高。即即使在沿观测方向有较大的位移,在重投影误差上仅导致很小的变化。因此,我们需要在非线性细化开始时有一个良好的焦距的初始估计,以实现收敛到正确的解决方案。为此,我们可以使用从EXIF数据中提取的焦距信息(如果可用的话)。然而,crowd-sourced照片经常因为修改而缺少这些信息,比如调整大小、裁剪等等。对于较大的变焦因子,仅仅假设默认的焦距[10,26]是不够的,从图像尺寸推断,并使用它作为非线性细化的初始估计。相反,在2D-3D pose估计期间,有必要对一个焦距的先验指定空间进行详尽采样。如果EXIF信息是缺失的,我们使用P3P RANSAC为[5◦,130◦]之间的开角均匀采样50个焦距,且使用有着最高inliers数量的解决方案,之后跟着一个pose的非线性细分。
然而,即使经过这些修改,由于低冗余、虚假的EXIF信息,或不幸的配置,相机配准偶尔仍然失败。我们检测这些情况是为了避免由于最初的坏相机的错误三角测量导致的级联配准错误。这些情况可以在SfM管道的不同阶段检测到。首先,在RANSAC pose估计中检测少量的inliers。其次,实现初始配准的非线性细化;错误的配准通常导致高成本的pose非线性细化。因此,我们拒绝显示上述任何属性的相机配准。第三,对于不完善的配准,bundle-adjustment通常收敛到局部最小值。因此,它试图通过使用极端的相机参数来最小化成本。当我们在bundle-adjustment中优化结构和运动时,我们过滤了有异常相机参数的图像(即开角在[5◦,130◦]以外、radial distortion参数的绝对值大于1)。
7. Densification
我们提出的结合SfM和检索系统实现了比最先进的重建系统更详细的重建。然而,场景的某些部分有着很差的细节。这种情况发生在在没有考虑完整的三维场景信息的情况下,通过图像检索得到的初始图像集在结构的某些区域没有提供足够数量的详细图像,甚至根本没有这样的图像。
然而,我们希望在结构的所有部分都能制作出高细节的完整模型。为了克服这一限制,我们引入了一种增量策略,通过显式挖掘原始重构三维模型低分辨率部分的高细节来扩展初始三维模型。为了避免无处不在的冗余的细节挖掘,我们建议在初始三维重建后按需进行细节挖掘。在初始重建后,我们能够确定稀疏模型的密度和识别三维模型的低分辨率部分。然后,我们尝试只对那些部分进行致密化重建。
为了发现覆盖了低分辨率部分的图像,我们首先通过计算在世界坐标系中每个图像观测值的空间范围来确定每个3D点的最高模型分辨率 ,即back-projecting 3D点的图像像素到世界坐标系上。由于来自不同距离和不同缩放级别的多个图像可能看到相同的结构,因此3D点被指定为所有观测值中分辨率最高的点。考虑到整个结构和相机poose的分辨率,我们就可以识别覆盖场景低分辨率部分的图像。每张图片通常只能看到整个场景的一小部分。在一幅图像中观察到的3D点分辨率的中位数为我们提供了一种有意义的测量方法,可以衡量一幅图像对其表面分辨率的整体贡献,而不依赖于对单个结构的距离或缩放级别。在最后一步中,我们按中值分辨率对所有图像进行排序,并迭代地查询顶部图像的更多细节,直到没有进一步的细节被发现,或者得到了足够的分辨率。最后,我们使用第5节中描述的策略,通过只匹配新图像,将新的检索到的图像与现有的重建图像连接起来。
8. Duplicate scene structure
重复、对称或重复的场景结构是城市环境中常见的模式,由于潜在的相机误配和错误的三角划分[35,8,33]的级联,给增量SfM带来了挑战。这些相机配准错误是由于场景结构对称,使用基于RANSAC的[8]对其进行了错误的检索和配准。
对于由对称场景结构造成的问题,现有的解决方案为配准相机triplets[35]的后处理或整个模型的后处理[8,33]。然而,所有这些方法的主要缺点是,不正确的相机和错误的3D点可能会潜在地导致不稳定的模型。此外,当场景的某些部分有太多相互冲突的观察结果时,增量SfM可能会过早地停止模型的扩展。理想情况下,在模型的增量扩展期间可以避免这种错误配准。
我们发现,如果提供一组更渐进的过渡图像(如视频),则由对称结构引起混淆的可能性会大大降低。考虑到我们的检索系统能够抓取不同方向的图像,我们能够向SfM系统提供更循序渐进的图像序列。因此,在实践中,我们观察到对称结构的鲁棒性显著增强。例如,如果使用传统检索方法,凯旋门、圣母院和St. Vitus则一直产生对称问题,而我们的系统没有受到这些影响。
9. Experimental Results
在我们的实验中,我们使用了从Flickr下载的超过740万张图片的通用数据库,这些图片的关键词是著名的地标、城市、国家和建筑站点。我们使用单个图像作为检索(表1和图6)和后续重构的种子。


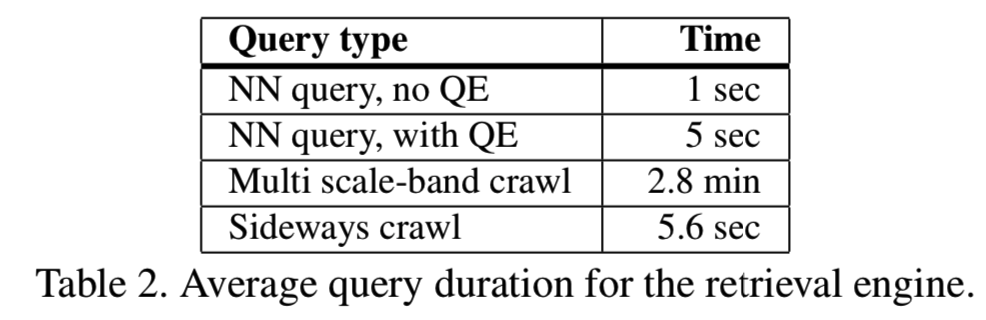
对于检索,每个查询的最大验证次数设置为5000次,表2总结了不同类型查询的平均时间。结合不同的查询类型,我们可以为一个给定的查询图像检索一组图像(以分钟为单位)。检索到的集合是一组简明的图像(少于整个数据库的0.1%),其中不相关的图像数量相对较少,配准的图像(registered images)与检索到的图像(retrieved images)的比率就是证明。请注意,配准的图像都是与查询图像相同的连接组件的一部分。高效匹配(第5节)允许我们在几个小时内构建单个模型,因为我们只需要对检索到的图像对执行匹配,而这些图像对是可能的图像对的一部分。
检索系统的各个组成部分对所获得的结果有不同的影响。sideways crawling有助于增加三维模型的范围,并消除重复/对称结构的歧义。在重建时没有sideways crawling(使用最先进的管道),凯门、圣维图和圣母院都有对称问题,不能完全重建——对于正面图像,前100位图像仍然是正面图像。放大(zoom out)提供了更多的上下文,我们已经观察到,它也有助于消除对称结构的歧义。例如,如果在不放大的情况下执行,巴黎圣母院左塔的两边是交叉匹配的。缩小(zoom in)并不能提高匹配的正确性,但可以显著提高细节的层次。
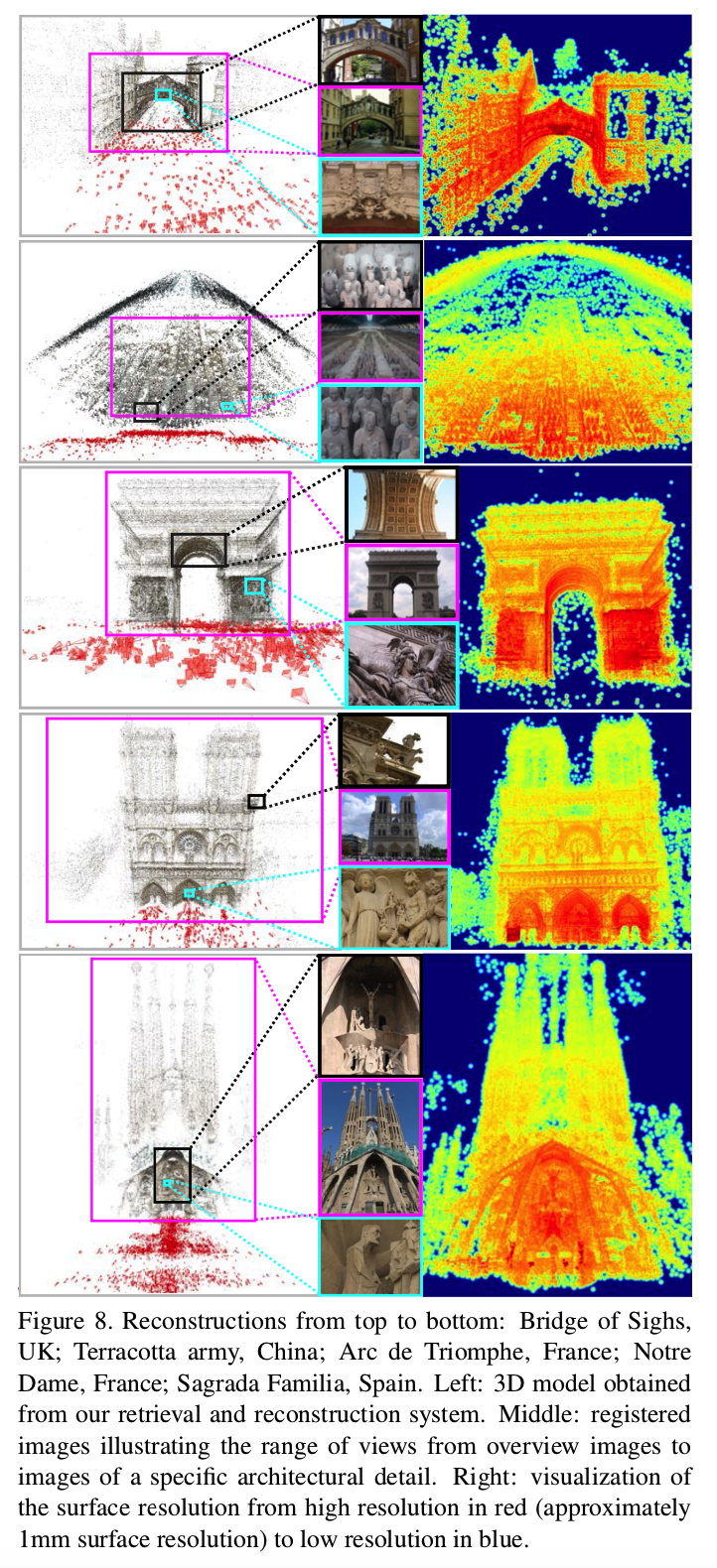
为了量化细节重建的数量,我们确定每个3D点的空间分辨率,如第7节所述。表面分辨率映射到jet color map进行可视化,其中红色表示最高分辨率,蓝色表示最低分辨率。图2和图8显示了各种场景的分辨率。此外,图7是使用多视图立体声进行密集重建的示例。

另一个实验表明,查询图像的选择并不是关键的。在凯旋门的场景中,从建筑相反侧面得到的两张不同的图像中提取出2640和2721张图像(union的交叉点92%),结果在视觉上几乎是相同的。
为了将我们的系统与完全两两重建方法相比较,我们将包含6036张图像的Dubrovnik6k数据集[14]注入到740万图像数据库中。从单个查询图像开始,我们的管道在前3次检索-sfm迭代重新构建87%(4430张图像),至于完全两两重建方法则是重建在孤立数据集(有着5102张配准图像)上。这两种方法的视觉质量相似,但对于我们的管道来说运行速度更快,尽管它运行在740万张图像上(而两两的方法运行在6K张图像上)。
10. Conclusion
我们提出了一种新的紧密耦合图像检索和SfM系统,用于从无序的互联网照片集合中重建详细的三维模型。我们的方法能够从单一的图像种子重建。重建和检索的紧密结合使我们能够从照片采集中检索到目前最先进的三维重建系统无法恢复的适合重建的图像数据。我们在从互联网上下载的740万张图片集合中的大量场景上演示了我们的方法。



