图像检索（image retrieval）- 7 - Aggregating Deep Convolutional Features for Image Retrieval - 1 - 论文学习

 

 2015

 Aggregating Deep Convolutional Features for Image Retrieval

Abstract

最近的一些研究表明，由深度卷积神经网络产生的图像描述符为图像分类和检索问题提供了最先进的性能。它还表明，卷积层的激活可以解释为描述特定图像区域的局部特征。这些局部特征可以使用为局部特征开发的聚合方法(例如Fisher向量)进行聚合，从而提供新的强大的全局描述符。

在本文中，我们研究了聚合局部深度特征以产生用于图像检索的紧凑全局描述符的可能方法。首先，我们发现深层特征和传统手工设计的特征具有完全不同的pairwise相似性分布，因此现有的聚合方法必须仔细地重新评估。这样的重新评估表明，相对于浅层特征，基于sum pooling的简单聚合方法对于深度卷积特征具有最好的性能。该方法是一种有效的方法，参数少，在学习主成分分析矩阵时不存在过拟合的风险。总的来说，新的紧凑型全局描述符在四个常见的基准上大大提高了最先进的水平。

 

1. Introduction

基于深度卷积神经网络(CNNs)[13]激活的图像描述符已经成为最先进的用于视觉识别的通用描述符[18,21,4]。最近的一些研究[2,21,7]提出使用最后的全连接网络层的输出作为全局图像描述符，并在描述符维数有限的情况下证明了它们对比先前的先进技术的优势。

近年来，研究重点从全连接层提取的特征转向CNNs的深卷积层特征[5,22,14](下面我们将这些特征称为深度卷积特征)。这些特征具有非常有用的特性，例如，它们可以直接和有效地从任意大小和高宽比的图像中提取出来。此外，卷积层的特征被自然地解释为对应于特定特征的接受域的局部图像区域的描述符。这样的特征可以看作是手工制作的“浅”特征的类比，比如dense SIFT[16,26]特征。也许是受到这种类比的启发，[15]建议使用这些特征来识别有意义的对象部分，而[5]建议使用在这些局部特征上构造的Fisher vector[23]来生成一个全局图像描述符，其在外部数据集上提供最先进的分类性能。

本文的重点是图像检索，特别是图像检索的全局描述符的构造。根据最近的论文[2,7,21,22]，我们考虑基于预训练的深度神经网络的激活的描述符，特别是神经网络的深度卷积层。考虑到新兴的在卷积层的特性感知，将其称为“new dense SIFT”[15,22,5,14],重用用于dense SIFT的最先进的embedding-and-aggregation框架，如VLAD [9], Fisher vectors [19] or triangular embedding [10],并将它们应用于深卷积特性。我们的第一个贡献是评估这些方法(特别是Fisher vectors和triangular embedding)以及更简单的聚合方案(如sum pooling和max pooling)。

令人惊讶的是，我们发现用于深度卷积特征的聚合方法的相对性能与用于浅层描述符的方法大不相同。特别是，一个基于sum pooling聚合的没有高维的嵌入，但具有简单的后处理操作的简单全局描述符，其性能非常好。这种基于sum pooling的卷积特征(SPoC描述符)的描述符在很大程度上提高了标准检索数据集上的紧凑全局描述符的最新水平，并且在检索方面的性能比之前在[2,7,22]中提出的深度全局描述符要好得多。除了出色的检索精度之外，SPoC特性还具有计算效率高、实现简单和几乎不需要调优超参数的特点。

重要的是，SPoC特征的性能优于深度卷积特征的Fisher vectors和triangular embedding。这与dense SIFT情况形成了鲜明的对比，在dense SIFT情况下，原始特征的sum pooling不会产生一个具有竞争力的全局描述符。我们进一步研究了深度卷积特征与浅层特征(SIFT)性能不同的原因，表明深度卷积特征具有较高的识别能力和不同的分布特性，因此不需要进行初步的embedding步骤。对这一主张提供了定性解释和实验证实。

总体而言，本文介绍并评价了一种新的简单紧凑的全局图像描述符，并探讨了其成功的原因。在公共检索基准测试中，描述符的性能优于现有方法。例如，在使用256维表征的Oxford数据集(在查询过程中使用整张图像时)上，得到了0.66 mAP的性能。

 

2. Related work

Descriptor aggregation. 将一组局部描述符(如SIFT)聚合成全局描述符的问题已经得到了广泛的研究。最著名的方法是VLAD [9]， Fisher Vectors[19]，以及最近的triangular embedding[10]，它构成了最先进的“hand-crafted”特性，如SIFT。

让我们回顾一下这些方案背后的思想(使用来自[10]的符号)。图像使用特征集表示。我们的目标是将这些特性组合成一个有区别的全局表征。区分性是指具有相同物体或场景的两幅图像的表征比不相关的两幅图像的表征更相似(如在余弦相似度方面相似)。除了可区分之外，大多数应用程序都偏爱更紧凑的全局描述符，这也是我们在这里工作的重点。因此，根据某些归一化程序，通过主成分分析(PCA)降低了的维数。

 

常见的生成表征的方法包含两步：主要是embedding（嵌入）和aggregation（聚合）（可选择性地再跟上PCA操作，一般用来降维）。embedding步骤映射每个个别特征x到一个更高维的向量。然后实现映射特征的聚合。聚合的可能选择是一个简单的求和操作，当然也可以使用更先进的方法（如democratic kernel [10]）。

 

现有的框架在映射的方法选择上有所不同。比如，VLAD预先计算K个centroids 的码本，然后映射x到向量，其中k是x最近centroids的数量。Fisher vector嵌入的管道是相似的，除了它使用的是soft probabilistic quantization而不是在VLAD的hard quantization。它还包含关于个别特征的残差的到嵌入的二阶信息。Triangulation Embedding [10] 还使用了聚类centroids，并通过串联个别特征x和聚类centroids之间的归一化差别来嵌入该个别特征x。然后中心化、白化和归一化embedding 。

嵌入步骤的基本原理是提高个体特征的识别能力。没有这样的嵌入,一对自无关的图片的SIFT特征x_i,x_j有相当大的机会有一个较大的标量内积<x_i,x_j>值。这就成为了局部特征之间偶然的false positives匹配的来源，如果数据集足够大，图像之间也会发生false positives匹配(因为产生的全局描述符之间的相似性是由对局部特征之间的相似性聚合而来的[3,25])。嵌入方法(·)通常被设计用来抑制这种false positives。例如，VLAD嵌入抑制了码本中临近不同centroids的特征对之间的所有匹配(使对应的标量内积为零)。可以对其他嵌入执行类似的分析。

用高维映射抑制false positives有一定的缺点。首先，这种映射还可以抑制局部特征之间的true positives匹配。其次，这种嵌入通常包括学习大量的参数，如果训练集和测试集的统计数据不同，这些参数可能会发生过拟合。同样地，由于表征可以是非常高维的，它可能需要具有类似统计数据的保持数据来学习可靠的主成分分析和白化矩阵。为此，[10]提出使用PCA旋转和power-normalization来代替白化。最后，与更简单的聚合方案相比，高维嵌入的计算强度更大。

尽管存在这些缺点，但是高维嵌入总是与SIFT这样的特性一起使用，因为如果没有它们，生成的全局描述符的识别率就低得令人难以接受。在本文中，我们证明了与SIFT相比，原始深度卷积特征的相似性足够可靠，无需嵌入即可使用。在非嵌入特性上执行的简单的sum pooling聚合提供了与高维嵌入相当的性能。消除嵌入（embedding）步骤简化了描述符，导致更快的计算速度，避免了过度拟合的问题，并且总体上导致了一种新的最先进的用于图像检索的压缩描述符。

 

Deep descriptors for retrieval. 之前的一些研究已经考虑了使用深度特征进行图像检索。因此，开创性的工作[12]给出了利用从全连接层中提取的深度特征进行检索的定性例子。之后，[2]对这些特征在对相关数据集进行微调和不进行微调的情况下的性能进行了广泛的评估，总体报道PCA压缩的深度特征优于传统的类SIFT特征计算的紧凑描述符。

同时，在[7]中，提出了一种更高效的描述符，它基于提取图像的不同片段，将它们通过一个CNN，然后使用VLAD-embedding[9]来聚合全连接层的激活。与此相关，[21]的工作报告了很好的检索结果，它使用了来自CNN全连接层的几十个特征集，而没有将它们聚合到一个全局描述符中。

最后，最近的研究[1,22]对最后一个卷积层的sum pooling聚合得到的图像检索描述符进行了评估。在这里，我们展示了在最后一个卷积层上使用sum pooling聚合特性会带来更好的性能。这与将sum pooling聚合解释为 simplest match kernel [3]的实现是一致的，这在sum pooling的情况下是有缺陷的。

总的来说，与之前的工作相比[2,7,21,1,22]，我们显示了在描述符(SPoC)中大量的设计选择可以极大地提高描述符的准确性和效率。与这些工作相比，我们还讨论和分析了在描述符聚合上与研究主体的连接，并评估了几个重要的聚合备选方案。

 

3. Deep features aggregation

在这一节中，我们首先比较深度卷积特征和SIFTs的分布特性，并强调两者的区别。基于这些差异，我们提出了一种新的全局图像描述符，它避免了SIFTs所需的嵌入步骤，并讨论了几种与该描述符相关的设计选择。

在我们的实验中，深度卷积特征的提取是将一幅图像 I 通过一个预先训练好的深度网络，并考虑到最后一个卷积层的输出。让这个层由C个特征图组成，每个特征图有高度H和宽度W。然后用一组H×W的c维向量表示输入图像I，这是我们所处理的深度卷积特征。

3.1. Properties of local feature similarities

如[10]中分析的那样，原始SIFT特征的个体相似性是不可靠的，即不相关的图像patch可以产生非常接近的SIFT特征。深度特征预计会更加强大，因为它们是在监督的方式下从大量数据中学习到的。为了证实这一点，我们以两个实验的形式，对计算出的特征的相似性进行了比较。

Experiment 1 观察三种描述符匹配的patches(图1)，我们按照如下步骤来寻找这些patches:

• 对于Oxford Buildings数据集中的每一张图像，我们都提取了深度特征和dense SIFT特征。
• 我们通过有着64个成分的Fisher vector embedding来嵌入SIFT特征。
• 对于每个查询图像的每种特征类型(deep convolutional, original SIFT, embedded SIFT)，我们计算其特征与数据集中所有其他图像特征之间的余弦相似度。
• 我们从每幅图像的前10列表中考虑随机特征对的相似性，并可视化相应的图像patches(原始和嵌入的SIFT特征为全接受域，深卷积特征为接受域的中心)。

 

（就是当两张图得到的特征相似时，可视化他们之间对应的image patch，看两张图是否真的相似）

图1是通过该过程选择的特征对的随机子集(每个Oxford building一个随机选择特征对)，上面一行对应基于深度卷积特征的匹配，中间一行对应原始dense SIFT，下面一行对应embedded SIFT。正如预期的那样，深度特征产生的匹配中明显的false positive要少得多，因为它们通常对应同一对象，对光照/视点变化和小的变化具有明显的容错性。基于SIFT的匹配要糟糕得多，而且许多匹配都对应于不相关的图像patches。利用Fisher vector的SIFT特征的embedding提高了匹配质量，但仍不如深度特征的效果。

Experiment 2. 我们还研究了深度卷积特征和dense SIFTs的高维分布的统计。最重要的是，我们对具有最大范数（norm）的深度特性的分布感兴趣，因为这些特性对全局描述符的贡献最大。在接下来的实验中，我们也观察到它们是最具鉴别力的。我们使用sum pooling描述符进行检索，但我们只聚合了(1)1%的随机特征(2)1%的具有最大范数的特征。Oxford building数据集[20](1)中的mAP得分只有0.09，远远小于(2)中0.34的mAP。这验证了具有大范数的特征比随机特征具有更强的辨别能力。

对于不同类型的特征，我们希望调查由其个体相似性产生的匹配的可靠性。为此，我们将每个点到它最近邻居的距离与到数据集中随机点的距离进行比较。更详细地说，我们执行以下操作。从每个查询图像中，我们提取十个具有最大范数的深度特征，并为每个深度特征计算到其他图像所有深度卷积特征的距离。然后我们绘制一个图来说明到第k个邻居的距离如何依赖于它的索引k。对于每个查询特征，距离都通过除以给定特征和来自其他图像的所有特征之间的距离的中值来标准化。

我们对从不同深度层次的层中提取的三种卷积特征“conv3_1”、“conv4_1”和“conv5_4”执行此步骤，它们来自于OxfordNet[24]。我们也对dense SIFTs进行了这个实验，尽管在这种情况下，从每张图像中提取随机的特征，因为SIFT特征都被相同范数归一化了。对于所有类型的特征，我们使用200万个特征的子集作为参考集，每幅图像使用大约1000个特征。

图2显示了所有查询的平均曲线。它们表明，来自“conv5_4”层的高范数深度卷积特征有少量“非常接近”的近邻，它们比其他点要近得多。这与SIFTs相反，在SIFTs中，到最近邻的典型距离与到数据集中随机描述符的距离要近得多（？？？？这不是一样的意思吗？意思应该是说SIFTs的近邻数量比深度卷积特征的数量多）。这一事实表明，SIFT特征的密闭性信息少得多，它们的强相似性是不可靠的，容易出现意外的false positive匹配。有趣的是，“conv3_1”和“conv4”特征的个体相似性不如“conv5 4”特征的可靠(更深层次的特征具有更可靠的相似性)。

请注意，第二个实验是无监督的，因为我们在计算距离时没有考虑匹配的正确性。相反，第二个实验强调了深度卷积特征和SIFT特征在高维空间分布上的实质性差异。

这两个实验的结果都表明，来自最后一个卷积层的深度特征的个体相似性具有更强的辨别能力，这些相似性产生的匹配中的false positive数量应该比SIFTs更小，这是因为匹配更精确(实验1)，也因为高范数深度特征的近邻更少(实验2)。当需要将这些特征编码到全局描述符中时，这就可以绕过高维embedding步骤。

 

3.2. SPoC design

我们描述了SPoC描述符，它基于没有embedding的原始深度卷积特征的聚合。我们将从图像I中计算出的每一个深度卷积特征f 与 该特征在最后一个卷积层生成的map stack中的空间位置对应的空间坐标(x, y)关联起来。

Sum pooling. SPoC描述符的构造从深度特性的sum pooling开始:

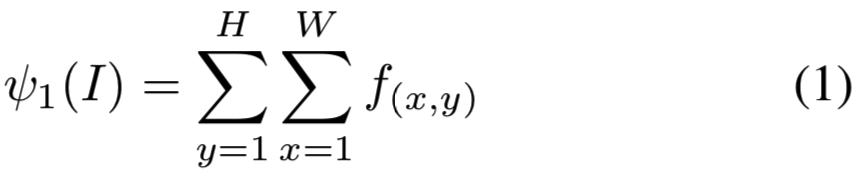
得到的描述符的标量积对应于一对图像之间最简单的匹配核[3]:

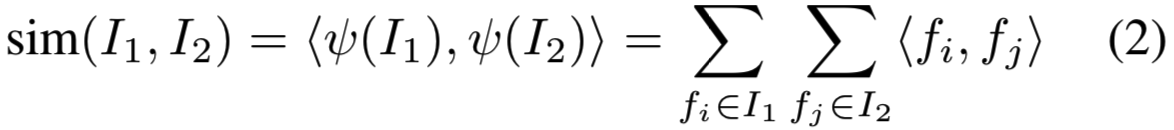
Centering prior. 对于大多数检索数据集，感兴趣的对象往往位于靠近图像几何中心的位置。可以通过一个简单的加权heuristics来修改SPoC描述符以包含这样的中心先验操作。这个heuristics算法给来自特征map stack的中心的特征分配更大的权重，将公式(1)改为:

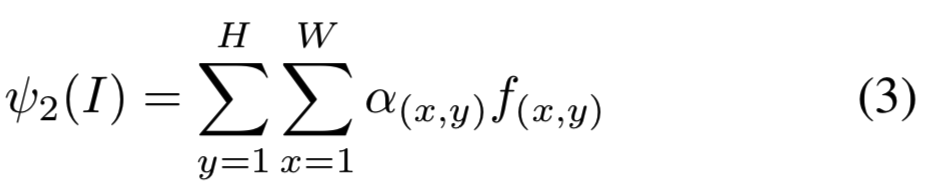
系数依赖于空间坐标h和w。我们使用的是高斯加权方案：

 

在这里，我们将σ这个参数设置为中心和最近边界之间距离的三分之一(这个特殊的选择来自于统计数据中的“three sigma”经验法则，尽管它显然与我们的使用没有直接关系)。虽然非常简单，但这个中心先验为一些数据集的性能提供了实质性的提高，这将在实验中显示。

Post-processing.获得的表征后面跟着L2归一化，并实现PCA压缩和白化：

其中M_PCA为大小为N×C的PCA矩形矩阵，N为保留维数，s_i为相关奇异值。

最后，对白化向量进行l2归一化:

注意，未压缩的的维数等于对应卷积层中的输出maps数。C的典型数值是几百，因此，具有中等的维度数。因此，在计算一个紧凑描述符时，估计SPoC的主成分分析矩阵和相关奇异值的数据要比Fisher向量或triangulation embedding少得多，因为它们对应的描述符的维数要高得多，而且过拟合的风险更高。下面的实验以及例如[10]的报告表明，这种过拟合可能是一个严重的问题。

  

4. Experimental comparison

Datasets. 我们在四个标准数据集上评估了SPoC和其他聚合算法的性能。

INRIA Holidays数据集[8](节假日)包含1491个假期快照，对应500个组，每个组具有相同的场景或对象。每个组中的一个图像用作查询（所以相同组的其他图像就是对应的ground truth图像，如果检索到的相似图像是同组的，则检索正确）。性能报告为对500个查询计算的mAP。与[2]类似，我们通过将图像旋转±90度来手动将其固定在错误的方向。

Oxford building数据集[20](Oxford5K)包含了来自Flickr的5062张与Oxford 地标相关联的照片。固定了对应11个建筑物/地标的55个查询，并提供了关于提供的这11个类在剩余数据集中的ground truth相关性（即标注剩下数据集中哪些图是其的相似图片，检索到这些图则算检索正确）。性能是通过对55个查询使用mean average precision(mAP)来衡量的。

Oxford Buildings dataset+100K [20] (Oxford105K) 这个数据集包含Oxford Buildings数据集和另外100K张来自Flickr的干扰图像。

University of Kentucky Benchmark dataset [17] (UKB) 包含2550个物体的10200张照片(每个物体4张照片)。每个图像用于查询数据集的其余部分。性能则是top 4结果中相同目标图像的平均数量来表示。

Experimental details. 我们使用由Simonyan和Zisserman[24]训练的非常深的CNN来提取深度卷积特征。CNNs使用Caffe[11]软件包。在这个架构中，最后一个卷积层的maps数为C = 512。所有图像在通过网络之前都被调整为586×586的大小。因此，最后一层的空间大小为W×H = 37×37。SPoC和其他方法的最终维数为N = 256。

Aggregation methods. 实验的重点是比较不同的深度卷积特征聚合方案。

我们考虑了简单sum pooling和max pooling聚合方法。此外，我们还考虑了两种更复杂的聚合方法，即Fisher vector [19] (Yael[6]实现)和Triangulation embedding [10](authors实现)。我们仔细地调整了这些方法的设计选择，以便使它们适应新的特性。

因此，对于Fisher vector，我们发现它有利于主成分分析——在嵌入前将特征压缩到32维。对于Triangulation embedding ，几个对SIFTs有强烈影响的调整在深度特征的情况下影响相对较小(这包括对初始特征的平方根和去除高能量的成分操作)。在系统比较中我们没有使用democratic kernel [10]，因为它可以应用于所有的embedding方法，而它的计算复杂度在某些情况下是令人望而却步的。我们观察到，对于Holidays数据集，它始终如一地将Triangulation embedding性能提高了2%(在PCA之前测量)。

在所有embedding方法之后使用PCA将其降至256维。对于sum pooling(SPoC)，接下来是进行白化，而对于Fisher vector和Triangulation embedding方法，我们使用了power normalization来避免过拟合(如[10]所建议的)。虽然[1]建议在max pooling聚合中使用白化方法，但我们观察到它会降低检索性能，因此我们没有在max pooling中使用白化方法。最后对所有表征进行L2归一化，使用标量积相似度(等同于欧氏距离)进行检索。除非另有说明，PCA(和白化)的参数是在保留的数据集上学习的(如Paris buildings for Oxford Buildings, 5000 Flickr images for Holidays)。

Results. 表1和表2比较了不同的聚合方法和SPoC的不同变体。

有几件事值得注意:

• 对于深度卷积特性，sum pooling在一定程度上是最佳的聚合策略。它优于同样简单的max pooling，即使存在下面讨论的缺陷, 它也优于Fisher vector和Triangulation embedding，这与SIFT特征形成鲜明对比。
• 我们在表2中演示过拟合对不同方法的适应性。我们可以看到，尽管用power normalization代替了白化方法，Fisher vector和Triangulation embedding还是会受到最终PCA的过拟合的影响。当在测试数据集上学习PCA时，它们的性能有了很大的提高。由于这种过拟合效果，使用更简单的聚合模型实际上是有益的:Fisher vector使用16 vs 256的混合分量，Triangulation embedding 使用1 vs 16的聚类中心。对于SPoC和max-pooling方法，过拟合非常小。
• 对于Triangulation embedding，具有一个centroid的退化配置性能最好(执行了比表中报告的更详尽的搜索)。即使没有主成分分析将最终描述符压缩到256维，我们也观察到，未压缩的描述符从使用多个centroid中获得的性能好处微乎其微，这与我们对深度卷积特征的统计数据的观察是一致的。
• Center prior方法为Oxford(a lot)、Oxford105K(a lot)和UKB(very little)数据集提供了帮助，但伤害了Holidays数据集一点点的性能。
• 白化对sum pooling比max pooling更有利(例如，max pooling在Oxford数据集使用白化获得0.48的mAP，而不使用白化则得到0.52的mAP)。显然，一些流行的特征在图像中是即常见又突发的，他们对SPoC的贡献被白化方法抑制了。对于max pooling来说，流行特性的突发性不是什么问题。
• 正如[2]中所观察到的那样，PCA压缩有利于深度描述符。在Oxford数据集中未压缩的(但仍然白化)SPoC特性得到0.55的mAP(压缩的效果为0.59 mAP)和在Holidays数据集中得到0.796的mAP效果(压缩后得到0.802的mAP效果)。

图3显示了一些使用SPoC描述符的好的和坏的检索示例的定性示例。我们还演示了查询图像的局部特征与数据集图像的全局SPoC描述符之间的相似性映射的一些示例。为了生成这些映射，我们使用SPoC构建相同的PCA+白化变换来压缩局部特征。然后计算查询图像的局部特征和数据集图像的SPoC描述符之间的余弦相似度，并将其可视化为热图。这样的热图允许定位一个查询图像的区域，类似于在搜索结果中的一个特定的图像。

 

表3给出了与最先进的紧凑全局描述符的比较。现有的研究对Oxford数据集使用不同的评估协议，例如[10,25]在检索前裁剪查询图像，而最近的研究[22,2,1,21]使用未裁剪的查询图像。这里，我们计算两种协议中的SPoC描述符。在crop情况下，对于查询图像，我们只聚合接受域的中心在查询边框内的特征(在基于SIFT的方法中通常是这样做的)。由于裁剪会丢弃一些上下文信息，因此croped查询的结果会比较低。

对于所有的评估设置(特别是在查询没有被裁剪的情况下)，Oxford5K和Oxford105K之间的性能差距非常小。这10万张Flickr干扰图片虽然对于hand-crafted特征（即SIFT等方法得到的特征）是“足够干扰的”，但并没有真正“干扰”到深度卷积特征，因为它们与Oxford Buildings的图片太不一样了。

与[2,7,22]中提到的深度描述符相比，SPoC特性提供了相当大的改进。有几种方法可以进一步改善结果。首先，将从同一幅图像的多个尺度提取的特征聚类在一起可以获得轻微的提升(在我们的初步实验中大约提升2%的mAP)。通过在一个专门收集的数据集上对原始CNN进行微调，也可以得到类似的改进(与[2]相同)。

 

 

5. Summary and Discussion

我们研究了几种将深度卷积特性聚合为紧凑的全局描述符的备选方案，并提出了一种基于简单的sum pooling聚合的新描述符(SPoC)方法。虽然SPoC的组件简单且已知，但我们展示了我们的设计选择的组合所产生的描述符比以前基于深度特征的全局图像描述符有了很大的提升，实际上也比以前最先进的紧凑全局图像描述符有了很大的提升。

除了提出一个具体的描述符外，我们还评估了针对上一代局部特征(SIFT)提出的高级聚合策略，并分析了为什么sum pooling为深度卷积特征提供了一个可行的替代方案。特别地，我们强调了局部卷积特征和dense SIFT之间的区别。我们的经验表明，深度卷积特征不应该被视为“新的dense SIFT”，因为当切换到新的特征时，针对SIFT等特征所建议的不同计算机视觉技术的相对性能必须被重新评估（而使用深度卷积特征则不需要重新评估）。