styleGAN相关 - Disentangled Inference for GANs with Latently Invertible Autoencoder(LIA) - 1 - 论文学习
Disentangled Inference for GANs with Latently Invertible Autoencoder
Abstract
生成对抗网络(GANs)在机器学习中扮演着越来越重要的角色。然而,有一个基本的问题阻碍了它们的实际应用:缺乏对真实示例进行编码的能力。解决这个问题的传统方法是通过变分自动编码器(VAE)学习GAN的编码器。在本文中,我们证明了VAE/GAN框架的潜在空间的纠缠性是编码器学习的主要挑战。为了解决GAN中的纠缠问题和推理问题,我们提出了一种新的算法——Latently Invertible Autoencoder (LIA)。LIA算法的框架是将一个可逆网络及其逆映射对称地嵌入到VAE的潜在空间中。首先将LIA的解码器decoder训练成一个具有可逆网络的标准GAN,然后通过将可逆网络与LIA分离,从一个解纠缠的自编码器那里学习部分编码器,从而避免了随机潜在空间造成的纠缠问题。在FFHQ人脸数据集和三个LSUN数据集上进行的实验验证了LIA/GAN的有效性
1 Introduction
深层生成模型在破解计算机视觉和其他学科的挑战中发挥着越来越重要的作用,如高质量图像生成 (Isola et al, 2017; Zhu et al, 2017; Karras et al, 2018a,b; Brock et al, 2018),文本到语音转换 (van den Oord et al, 2016, 2017), 信息检索 (Wang et al, 2017), 3D渲染 (Wu et al, 2016; Eslami et al, 2018), 和信号到图像的获取 (Zhu et al, 2018)。特别是,生成对抗网络(GAN) (Goodfellow等,2014)展示了一种学习高维图像数据分布的非凡能力。例如,通过StyleGAN算法(Karras et al, 2018b, 2019)生成的人脸和真实人脸变得无法区分。对抗性学习作为一种损失函数在许多机器学习应用中也被广泛应用。
然而,普通GAN的一个关键限制是缺乏对真实样本进行推断的编码器。也就是说,我们不能通过GAN架构直接推导出给定样本x对应的随机变量z。这是一个重要的问题,因为通过GANs的实际应用程序通常依赖于对潜在变量的操作,如域适应、数据增强和图像编辑。
处理这一问题的现有办法分为三类,摘要见表1。常用的方法称为GAN反演,它基于生成样本和相关实际样本之间的均方误差(MSE)的优化 (Radford et al, 2016; Berthelot et al, 2017)。这类算法主要存在两个缺点:对z的初始化比较敏感,计算时间比较长。第二类称为对抗性推理(Dumoulin et al, 2017; Donahue et al, 2017),该方法使用另一种GAN在对偶GANs框架中将z推断为潜在变量。对抗性推理一般强调对象的高级表示,而不是旨在忠实地重建样本 (Donahue and Simonyan, 2019)。执行GAN推断的另一种自然方法是通过VAE算法的原理来调整编码器,提供一个预先训练过的GAN模型(Luo et al, 2017),或者端到端学习整个VAE/GAN架构(Larsen et al, 2016)。VAE和带有共享的解码器/生成器的GAN相结合的框架实际上是一种很好的GAN推理解决方案。然而,VAE/GAN所面临的一个问题是,其重建精度往往低于单独使用VAE的方法,重建样本的质量往往低于从预先训练的GANs中采样生成的样本的质量。我们将在第6节中对此进行更详细的分析。

在本文中,我们验证了潜空间的解耦是VAE/GAN编码器学习质量的决定性因素。在此基础上,我们建立了一个新的模型,称为Latently Invertible Autoencoder (LIA)。LIA利用可逆网络在潜在空间中以对称的方式桥接编码器和解码器,从而通过dual学习形成LIA/GAN框架,用于GAN的生成和推理。LIA/GAN的体系结构如图2所示。我们总结其主要优势如下:
- 我们证明了潜在空间(z-空间)中的纠缠和中间潜在空间(y-空间)中的解纠缠的影响。我们认为,GAN训练过程中形成的潜在空间的纠缠是造成VAE/GAN效果不佳的主要原因。在此基础上,我们提出了LIA的体系结构和相应的两阶段训练方案。
- LIA中可逆网络的对称设计带来了两个好处。先验分布可以从一个解纠缠和展开的特征空间中精确地拟合,从而极大地缓解了推理问题。此外,由于在训练编码器时潜在空间是分离的,因此可以不需要变分推理来训练编码器VAE。
- 两阶段对抗式学习将LIA框架分解为具有可逆网络的普通GAN和无随机变量的标准自编码器VAE。因此,编码器的训练是确定性的,是通过解耦潜在空间进行的,这意味着我们的模型在训练VAE时不会受到纠缠问题的影响。
- 我们在推理和生成/重建时将LIA与最先进的GAN模型相比较。在FFHQ和LSUN数据集上的实验结果表明,该算法取得了较好的性能。
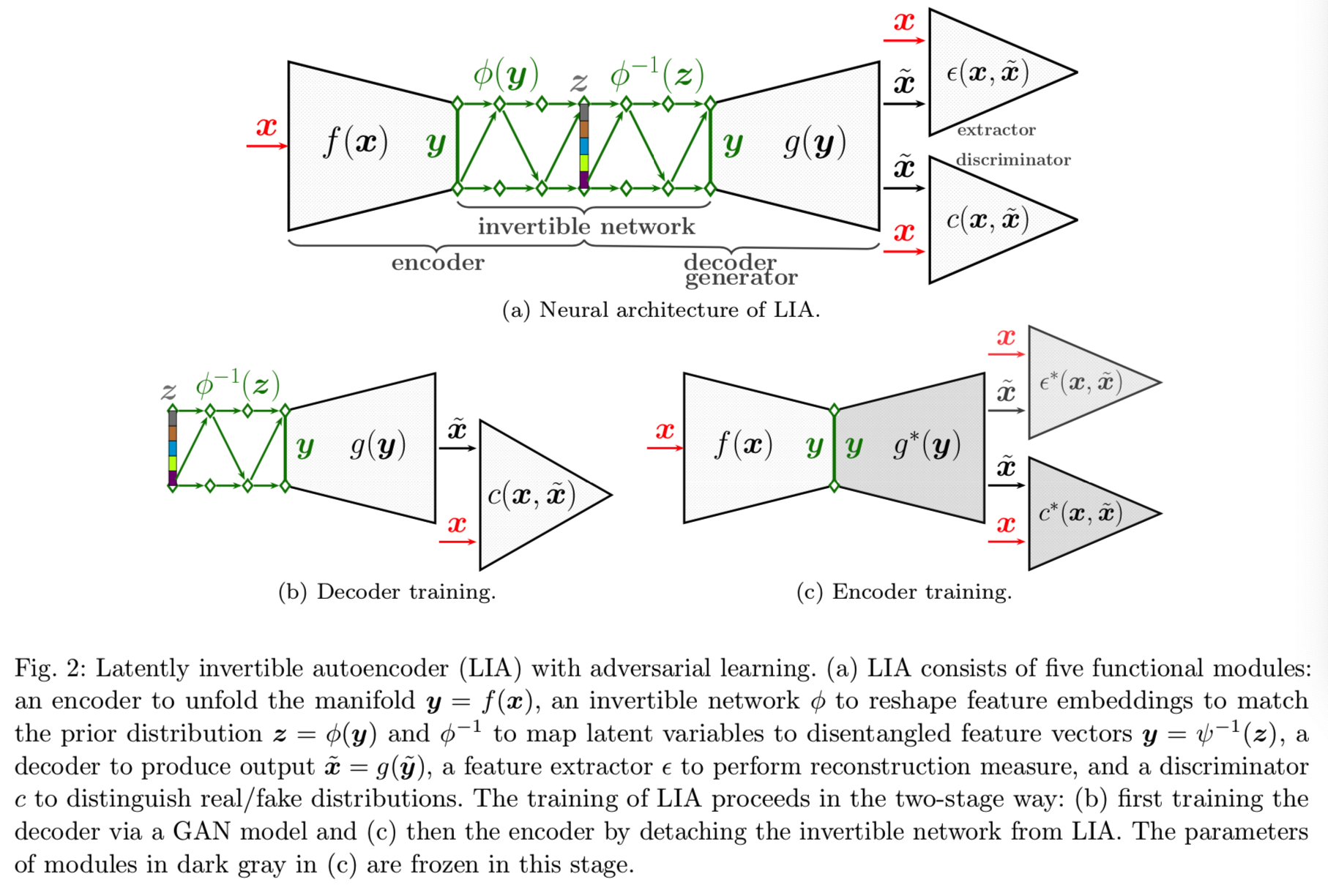
该图可见该架构就像是styleGAN+encoder
2 Entanglement in GANs
在本节中,我们对GANs中纠缠和解纠缠的影响、数学原理以及对图像重建的意义进行了实证分析。
2.1 Entanglement from Random Mapping
对于一个GAN模型,有![]() ,其中g是一个生成器,z通常是从一个带有均值为0和单位方差的高斯先验中采样得到的,即
,其中g是一个生成器,z通常是从一个带有均值为0和单位方差的高斯先验中采样得到的,即![]() 。为了可视化GANs中的耦合,随机采样zi和zj并在他们之间进行线性插值。对应的生成样本能够通过
。为了可视化GANs中的耦合,随机采样zi和zj并在他们之间进行线性插值。对应的生成样本能够通过![]() 获得。如通过在FFHQ数据集中训练得到的StyleGAN模型得到的可视化在图1(a)中的结果可知,在从人脸
获得。如通过在FFHQ数据集中训练得到的StyleGAN模型得到的可视化在图1(a)中的结果可知,在从人脸![]() (对应zi)变形(即插值)到人脸
(对应zi)变形(即插值)到人脸![]() (对应zj)时,人脸的身份有显著的变化,这意味着在
(对应zj)时,人脸的身份有显著的变化,这意味着在![]() 中的人脸并不随着在z-space的线性变化进行连续变化。作为对比,我们通过一个中间潜在变量
中的人脸并不随着在z-space的线性变化进行连续变化。作为对比,我们通过一个中间潜在变量![]() 去建立映射函数,就和styleGAN所做的一样,,其中φ是用来生成与z有相同维度的输出向量y的多层感知机。从图1(c)可见,与y插值相关的人脸path离直线(灰色虚线)的距离比与z插值相关的人脸path近,同样的其对应的生成人脸的变化也更平滑,如图1(b)所示。
去建立映射函数,就和styleGAN所做的一样,,其中φ是用来生成与z有相同维度的输出向量y的多层感知机。从图1(c)可见,与y插值相关的人脸path离直线(灰色虚线)的距离比与z插值相关的人脸path近,同样的其对应的生成人脸的变化也更平滑,如图1(b)所示。
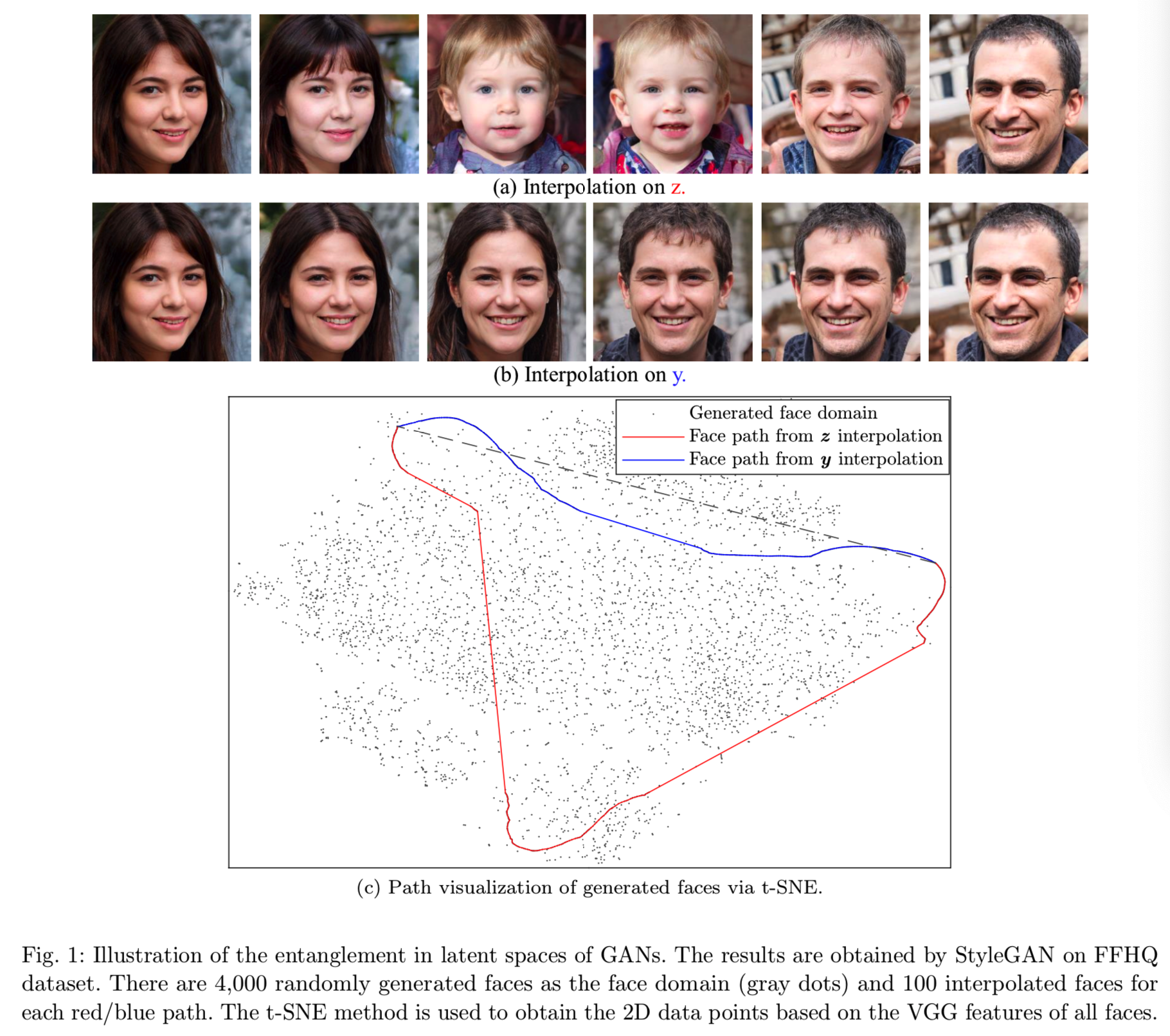
实际上,这是任意两个变化较大的人脸之间的z和y插值的一个非常普遍的现象。根据Karras et al (2018b),我们将生成人脸的折叠z空间称为纠缠潜在空间,中间潜在空间(即y)称为解纠缠潜伏空间。z带来的纠缠是由在随机采样中训练的GAN招致的,因为没有几何约束保证z、![]() 之间的空间邻接的相关性。结论就是当人脸
之间的空间邻接的相关性。结论就是当人脸![]() 和人脸
和人脸![]() 在感知上是相似的时,其相关zi和zj的空间位置不是一定要邻近的。y-space的解纠缠性将在2.3部分分析
在感知上是相似的时,其相关zi和zj的空间位置不是一定要邻近的。y-space的解纠缠性将在2.3部分分析
2.2 Inference Difficulty from Entanglement
为了不失一般性,我们将优化写为:
![]()
其中![]() 表示step为t时z的梯度。这里z可能是先验或VAE中encoder的输出,即
表示step为t时z的梯度。这里z可能是先验或VAE中encoder的输出,即![]() 。为了使问题容易理解,我们假设生成样本
。为了使问题容易理解,我们假设生成样本![]() 也是一个人脸。让
也是一个人脸。让![]() 表示人脸
表示人脸![]() (或一个目标类)的身份。如果
(或一个目标类)的身份。如果![]() 能与
能与![]() 在语义上可区分,且
在语义上可区分,且![]() 如图1(a)所示,那么纠缠就会出现,其中z0和zT是初始和收敛目标。那么在图1(c)所示的优化过程中,zt路径可能会发生纠缠,导致算法难以在正确的极小值处收敛。通过以上分析,我们认为VAE/GAN和基于MSE的优化方法无法很好地对GANs进行推理的关键是z空间的纠缠问题。实践证明,在优化过程中,纠缠会导致梯度波动过大,影响算法的收敛,这将在6.5节进行分析。
如图1(a)所示,那么纠缠就会出现,其中z0和zT是初始和收敛目标。那么在图1(c)所示的优化过程中,zt路径可能会发生纠缠,导致算法难以在正确的极小值处收敛。通过以上分析,我们认为VAE/GAN和基于MSE的优化方法无法很好地对GANs进行推理的关键是z空间的纠缠问题。实践证明,在优化过程中,纠缠会导致梯度波动过大,影响算法的收敛,这将在6.5节进行分析。
2.3 Disentanglement and Lipschitz Continuity
GANs的解纠缠可以用Lipschitz连续性来表示。对于GAN模型,我们可以编写:
![]()
其中C是Lipschitz常量,vi和vj是变量。不等式(2)说明了两个生成样本![]() 之间的距离不大于变量vi和vj之间的距离乘以一个常数的值。对于映射
之间的距离不大于变量vi和vj之间的距离乘以一个常数的值。对于映射![]() ,我们可以很简单地找到不满足等式(2)的失败案例,如图1所示。可是对于来自中间潜在空间的映射
,我们可以很简单地找到不满足等式(2)的失败案例,如图1所示。可是对于来自中间潜在空间的映射![]() ,Lipschitz连续性在一些条件下是满足的,即:
,Lipschitz连续性在一些条件下是满足的,即:
![]()
可见,我们需要g(y)的 Jacobian矩阵 J,即Jij = ![]() 。被(Karras et al, 2019) 揭露的等距g-mapping说明了当
。被(Karras et al, 2019) 揭露的等距g-mapping说明了当![]() 满足时,
满足时,![]()
![]() 成立,其中
成立,其中![]() 表示单位矩阵,a时一个常量,T表示转置。因此Jacobian regularizer被应用在(Karras et al, 2019)中去加强关于y的生成器的解耦。此外,spectral normalization(光谱归一化,Miyato et al, 2018)也有助于Lipschitz的连续性。
表示单位矩阵,a时一个常量,T表示转置。因此Jacobian regularizer被应用在(Karras et al, 2019)中去加强关于y的生成器的解耦。此外,spectral normalization(光谱归一化,Miyato et al, 2018)也有助于Lipschitz的连续性。
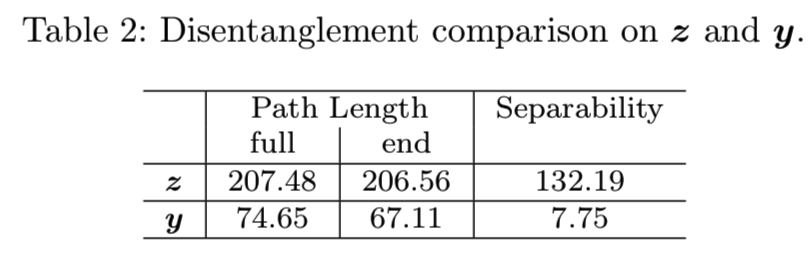
在实际应用中,我们发现映射网络后的Lipschitz连续性足以通过嵌入GANs中的深映射y = ![]() 来建立一个解纠缠的中间潜伏空间,如图1所示。Karras等(2019)采用的路径长度指数可以反映Lipschitz连续性的性质。为了进一步揭示这一现象,我们分别比较了随机采样z和y生成的人脸的路径长度。从表2可以看出,来自y的路径长度要比来自z的路径长度短得多,这证明了y空间接近Lipschitz,因此更加解耦。
来建立一个解纠缠的中间潜伏空间,如图1所示。Karras等(2019)采用的路径长度指数可以反映Lipschitz连续性的性质。为了进一步揭示这一现象,我们分别比较了随机采样z和y生成的人脸的路径长度。从表2可以看出,来自y的路径长度要比来自z的路径长度短得多,这证明了y空间接近Lipschitz,因此更加解耦。
所以这里不采用直接用z来生成图像,而是先将z映射成y,再用y生成图像
Lipschitz连续性可以保证潜在空间与生成样本空间的空间一致性,有利于推理任务的完成。因此,我们设计了基于解耦的y空间而不是z空间的GAN推理算法。
3 Latently Invertible Autoencoder
如前面部分所分析的,为了获得解耦的潜在编码,我们需要在原始的GAN结构中嵌套一个映射网络,即![]()
![]() 。同时,encoder f直接推理y去满足解耦性。所以我们需要建立一个反向的映射去获得来自y的z,即
。同时,encoder f直接推理y去满足解耦性。所以我们需要建立一个反向的映射去获得来自y的z,即![]() ,其中
,其中![]() 。因此一个可逆神经网络可以建立在z和y之间的可逆性。LIA框架根据该规则建立起来。细节如下所示。
。因此一个可逆神经网络可以建立在z和y之间的可逆性。LIA框架根据该规则建立起来。细节如下所示。
3.1 Neural Architecture of LIA
如图2(a)所示,在VAE的潜在空间对称嵌入一个可逆神经网络,其映射过程如图所示:

其中Φ为可逆网络的深层复合映射。LIA首先对输入数据x进行非线性降维,并将其转换为低维解耦特征空间Rdy。f(x)对于LIA的作用可以看作是展开底层的数据manifold。因此,在该解耦特征空间中,线性插值和矢量算法等欧几里得运算更加可靠和连续。然后我们建立了一个从特征y到潜在变量z的可逆映射,而不是直接将原始数据映射到潜在变量的VAEs。通过变换矩阵z的可逆性,可以准确地恢复特征y,这是使用可逆网络的优点。然后将恢复的特征y送入部分解码器g(y),生成相应的数据![]() 。如果可逆网络的
。如果可逆网络的![]() 被删除了,LIA就变成了一个标准的autoencoder,即
被删除了,LIA就变成了一个标准的autoencoder,即![]()
一般来说,任何可逆网络都适用于LIA框架。我们在实践中发现,Dinh等人(2015)使用的一个简单的可逆网络足以构造从特征空间Rdy到潜在空间Rdz的映射。![]() 和
和![]() 分别是x和z的上下分量的形式。然后将可逆网络建立为:
分别是x和z的上下分量的形式。然后将可逆网络建立为:
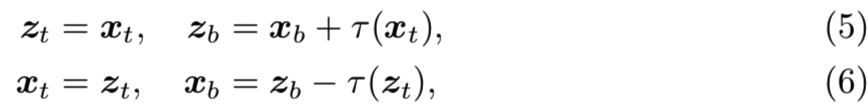
其中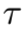 可以是任意可微函数的变换。或者,人们可以尝试利用具有仿射耦合映射的复杂可逆网络来完成更具挑战性的任务 (Dinh et al, 2017; Kingma and Dhariwal, 2018)。正如Dinh等人(2015)所做的那样,为了简单,我们设置
可以是任意可微函数的变换。或者,人们可以尝试利用具有仿射耦合映射的复杂可逆网络来完成更具挑战性的任务 (Dinh et al, 2017; Kingma and Dhariwal, 2018)。正如Dinh等人(2015)所做的那样,为了简单,我们设置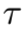 为一个带有leaky ReLU激活的多层感知机。
为一个带有leaky ReLU激活的多层感知机。
3.2 Reconstruction Loss and Adversarial Learning
为了保证能精确重建 x̃ ,(变分)autoencoders的传统方式是使用距离![]() 或直接计算x和x̃之间的交叉熵。这里,我们利用了pixel损失和perceptual损失,其被证明对图像细节的变化更有鲁棒性(Johnson et al, 2016)。让ε表示特征提取器,如VGG (Simonyan and Zisserman, 2014)。然后我们就可以表示损失为:
或直接计算x和x̃之间的交叉熵。这里,我们利用了pixel损失和perceptual损失,其被证明对图像细节的变化更有鲁棒性(Johnson et al, 2016)。让ε表示特征提取器,如VGG (Simonyan and Zisserman, 2014)。然后我们就可以表示损失为:
![]()
其中β1是平衡两个损失的超参数。这种混合重建损失的可行性在不同的图像到图像的转换任务中是明显的。ε本质上是产生输入x和输出x̃表征的函数。ε的获得是相当灵活的。它可以通过监督学习或无监督学习获得,这意味着可以使用类标签,如VGG(Simonyan and Zisserman, 2014)或不使用类标签 (van den Oord et al, 2018)来训练ε。
在autoencoder-like架构中,基于norm的重构约束通常会导致输出图像模糊(Lehtinen et al, 2018)。这个问题可以通过对抗性学习来解决(Goodfellow et al, 2014)。为此,鉴别器c用来平衡x和x̃之间比较的损失。使用Wasserstein GAN(Arjovsky et al, 2017; Gulrajani et al, 2017),我们可以将优化目标写为:
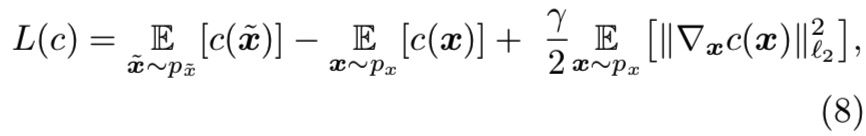
其中![]() 分别表示真实数据和生成数据的概率分布。γ是正则化的超参数。R1正则化器在(Mescheder et al, 2018)中被证明收敛更稳定。在实践中, 蒙特卡洛抽样近似得到的sliced Wasserstein距离优先执行
分别表示真实数据和生成数据的概率分布。γ是正则化的超参数。R1正则化器在(Mescheder et al, 2018)中被证明收敛更稳定。在实践中, 蒙特卡洛抽样近似得到的sliced Wasserstein距离优先执行![]() 的比较(Karras et al, 2018a)。
的比较(Karras et al, 2018a)。
4 Two-Stage Training
我们提出了一种两阶段训练方案,将框架分解为两部分,分别进行端到端的良好训练,如图2(b)和(c)所示。首先,将LIA的解码器训练为具有可逆网络的GAN模型。其次,将连接特征空间和潜在空间的可逆网络从架构中分离出来,将框架简化为一个没有变分推理的标准自编码器。因此,这种两阶段设计防止了耦合问题。
4.1 Decoder Training
ProGAN (Karras et al, 2018a), StyleGAN (Karras et al, 2018b, 2019), 和BigGAN (Brock et al, 2018) 能够从一些先验分布的随机噪声采样中生成逼真的图像。那自然就会假设如果我们能找到给定x的潜在变量,这样的GAN模型适用于精确恢复x̃。也就是说,我们可以分别在LIA框架中训练关联GAN模型。为了做到这一点,我们为第一阶段的训练挑选出一个标准的GAN模型,如图2(b)所示,其图解可以被形式化为:
![]()
z直接从一个预定义的先验中采样。根据Wasserstein GAN原理,优化目标为:
![]()
上标∗表示对应映射的参数已经学过了。值得注意的是,可逆网络在这里的作用就是它的变换可逆性。与归一化流相比,我们对z和Φ(y)的概率没有任何限制。我们在生成器前附加一个可逆网络的策略可以潜在地应用于任何GAN模型。
这一步的作用就是用来训练g生成器,让其由z->y得到的重构图与真实的图是相似的,将生成器训练好,然后将其参数frozen用于训练下面的f(其实可以等价于训练一个styleGAN模型,其中的y对应于其的w)
4.2 Encoder Training
在LIA结构中,可逆网络以对称的方式嵌入到潜在空间中,即![]() 。可逆网络的这一独特特性使我们能够从LIA的框架中分离出可逆网络。这样我们就得到了一个无随机变量的常规自编码器,如图2(c)所示。其图解为:
。可逆网络的这一独特特性使我们能够从LIA的框架中分离出可逆网络。这样我们就得到了一个无随机变量的常规自编码器,如图2(c)所示。其图解为:
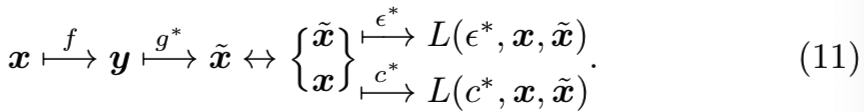
在实践中,感知损失的特征提取器ε是在ImageNet数据集上预先训练的权重用到conv4的VGG。在第一阶段GAN训练后,f的参数被学习为:
![]()
其中,β2是超参数,c**是鉴别器的微调参数,这意味着当生成器冻结时鉴别器会随着编码器的训练进行微调。上述服务于图2(c)架构的优化在计算机视觉中得到了广泛的应用。它是用于不同图像处理任务的各种GANs的主干框架 (Isola et al, 2017; Zhu et al, 2017)。但是对于LIA来说,它要简单得多,因为我们只需要学习部分编码器f。这种两阶段训练带来的简单性可以强制编码器收敛到更精确的推断。
这一步就是使用上一步训练好的生成器g,然后再训练出一个f,让该f能够输入一张图x,得到一个潜在编码y,且这个y就能够作为g的输入,并能很好地重构出输入的图x
5 Related Work
我们的LIA模型与用对抗性学习解决VAEs的推理问题的工作以及为GANs设计编码器的工作有关。GAN与VAE的整合可以追溯到VAE/GAN (Larsen et al, 2016)和隐式自编码器(Makhzani et al, 2015; Makhani, 2018)。这些方法遇到端到端训练的困难,因为梯度在经过深层复杂架构的潜在空间后容易变得不稳定(Bowman et al, 2015; Kingma et al, 2016)。此外,还有一个有趣的尝试,以对抗的方式训练VAE (Ulyanov et al, 2017; Heljakka et al, 2018) 。这些方法面对的是执行推断和比较真/假分布的编码器角色之间的权衡。这很难调节。因此,我们更倾向于向原始GAN的框架中添加一个必不可少的鉴别器。
LIA的相关工作即将 VAE 与 反向自回归流(Kingma et al, 2016) 和 基于潜在流的VAE方法(即VAEs带有使用归一化流(Su and Wu, 2018; Xiao et al, 2019)条件化的潜在变量)相结合的模型。这三种模型都需要优化归一化流的对数似然,这与LIA有本质的不同。LIA中的可逆网络仅用于建立耦合z空间与解耦y空间之间的可逆性。对于LIA中涉及的归一化流,不存在概率优化。还有一些替代的尝试,如指定使用归一化流(Grover et al, 2017)的GAN的生成器 或使用部分可逆网络 (Lucas et al, 2019)将图像映射到特征空间。这些方法都存在高维的高复杂度计算问题。Luo et al(2017)的两阶段训练方法存在耦合问题。
值得注意的是,我们这里关注的重建任务与最近的表征学习工作不同,表征学习使用对抗式推理来学习特征进行识别和分类 (Dumoulin et al, 2017; Donahue et al, 2017; Donahue and Simonyan, 2019)。我们的主要目标是了解真实图像的潜在代码,并进一步忠实地从潜在代码中重建真实图像,用于后续任务,如图像编辑。图像编辑的性能完全取决于重建精度,而对抗性推理的工作如 Dumoulin et al (2017); Donahue et al (2017); Donahue and Simonyan (2019) 更喜欢学习对分类任务有利的高级语义特征。这些目标本质上是不同的。
我们意识到一个并行的工作,称为对抗潜在自动编码器(Adversarial Latent Auto-Encoders,ALAE) (Pidhorskyi et al, 2020),提出了一个类似的想法。ALAE和我们的LIA方法有四个关键的区别。
首先,ALAE使用的基于样式的编码器encoder比我们的更加复杂。对于LIA,编码器的架构没有特殊的约束。其次,ALAE的编码器也是用于重构损失的特征提取和鉴别器的主要模块,可以对整个算法进行端到端的训练。然而,LIA可以与任何GAN框架集成,因为它具有更灵活的模块化设计和两阶段训练方案。第三,我们明确地解释和揭示了GAN推理需要在确定性y空间而不是随机z空间中执行的潜在原因。最后,对于LIA, y空间和z空间是完全可逆的,这为相互研究提供了一种方便的方法。我们将在实验部分演示这种可逆性的应用。
6 Experiments
对于实验设置,我们用StyleGAN的生成器实例化LIA的解码器decoder(Karras et al, 2018b)。不同之处在于我们用可逆网络代替了StyleGAN中的映射网络(MLP)。可逆网络的层数为8。该鉴别器的超参数分别为:等式(8)的γ=10,等式(7)的β1=5e-5,等式(12)的β2=0.1。对于式(7)中的感知损失,我们从VGG权重中取其ε = conv4_3。
我们比较的生成模型是VAE和GAN (VAE/GAN)相结合的模型与基于MSE的GAN反演模型(Radford et al, 2016; Berthelot et al, 2017; Lipton and Tripathi, 2017),以及反向学习推理模型(ALI)(Dumoulin et al, 2017)。为了评估可逆网络的必要性,我们还训练了一个编码器和一个带有原始多层感知器的StyleGAN,表现为图3的最后一列。两阶段的训练方案与LIA一样使用。StyleGAN的产生和鉴别器与StyleGAN完全相同。

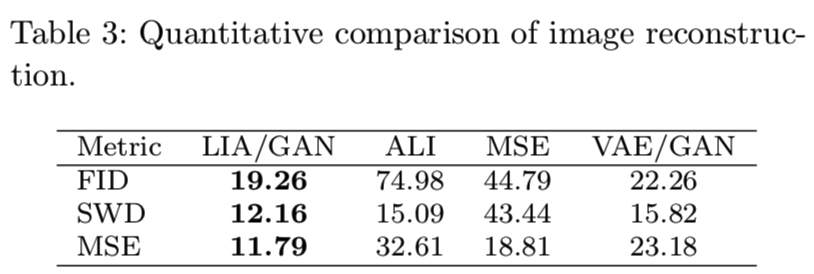
为了定量评估度量,我们使用Fr ́echet inception distance (FID), sliced Wasserstein distance (SWD), and mean square error (MSE)。这三个度量常用于度量GANs 的数字精度(Ulyanov et al, 2017; Karras et al, 2018a; Donahue et al, 2017; Karras et al, 2018b)。我们直接使用ProGAN (Karras et al, 2018a)作者发布的代码。用于z的Gaussian先验维度为512.
6.1 FFHQ Face Database
所有模型首先在StyleGAN的作者创建的Flickr-Faces-HQ (FFHQ)数据库上进行测试,作为基准。FFHQ包含70,000张高质量的人脸图像。我们将前65000个人脸作为训练集,剩下的5000个人脸按照数据集的确切顺序进行重构测试。我们不通过随机抽样来分割数据集,因为感兴趣的读者可以用我们的实验方案精确地复制所有报告的结果。
图3显示了所有模型的重建人脸。很明显,LIA的表现要比其他人好得多。ALI和VAE重建的脸看起来是正确的,但是质量很普通。ALI和VAE的思想是优雅的。他们的表现可能会因新技术而得到改善,如神经结构的逐步生长或基于style结构的成长。基于MSE的方法在人脸正常的情况下,可以得到与LIA质量相当的人脸部分。但当面部的变化变大时,这种方法就失败了。例如,失败来自于长头发、帽子、胡须和大的姿势。有趣的现象是,使用相同的训练策略,只有编码器的StyleGAN不能成功恢复目标人脸,即使它因为StyleGAN生成器,有能力生成高质量的真实人脸。这表明,可逆网络对LIA的工作起着至关重要的作用。表3中的定量结果显示了LIA的一致性优势。
利用LIA进行图像重构,方便了图像的语义编辑。图4是对重建人脸属性的处理结果,图5是对真实人脸的风格混合。


6.2 LSUN Database
为了在差异较大的数据上进一步评价LIA,我们使用了大型LSUN数据库(Yu et al, 2015)中的三个类别,即cat、car和bedroom。对于每个类别,通过排序算法(Zhou et al, 2003)从数据集中的前50万幅图像中选取10万幅图像。将猫和卧室图像分别调整为128×128,汽车图像调整为128×96进行训练。我们采用子集,因为它不会花费太长的训练时间来收敛,而仍然保持数据的复杂性。这些子集将供评价使用。
图6显示了LIA重建的对象忠实地维护了原始对象的语义和外观。例如,猫的胡须被恢复,表明LIA能够恢复非常详细的信息。可以看出,LIA明显提高了重构质量。提高主要来自于LIA的两阶段训练。通过对抗性学习训练的解码器保证了生成的图像的真实感(第一阶段)。通过对感知损失和对抗性损失的确定训练,保证了可以更精确地获得潜在特征向量(第二阶段)。通过将可逆网络分离编码器和解码器的设计,避免了学习编码器时后验概率的优化,使两阶段训练成为可能。图7显示了重建对象上的插值结果。我们可以看到,在变形过程中,物体被平滑地变形,并且保存了逼真的效果。在FFHQ和LSUN数据库上的实验结果验证了可逆网络的对称设计和两阶段训练成功地解决了GAN推理问题。


6.3 Finetuning the Latent Code to a Specific Image
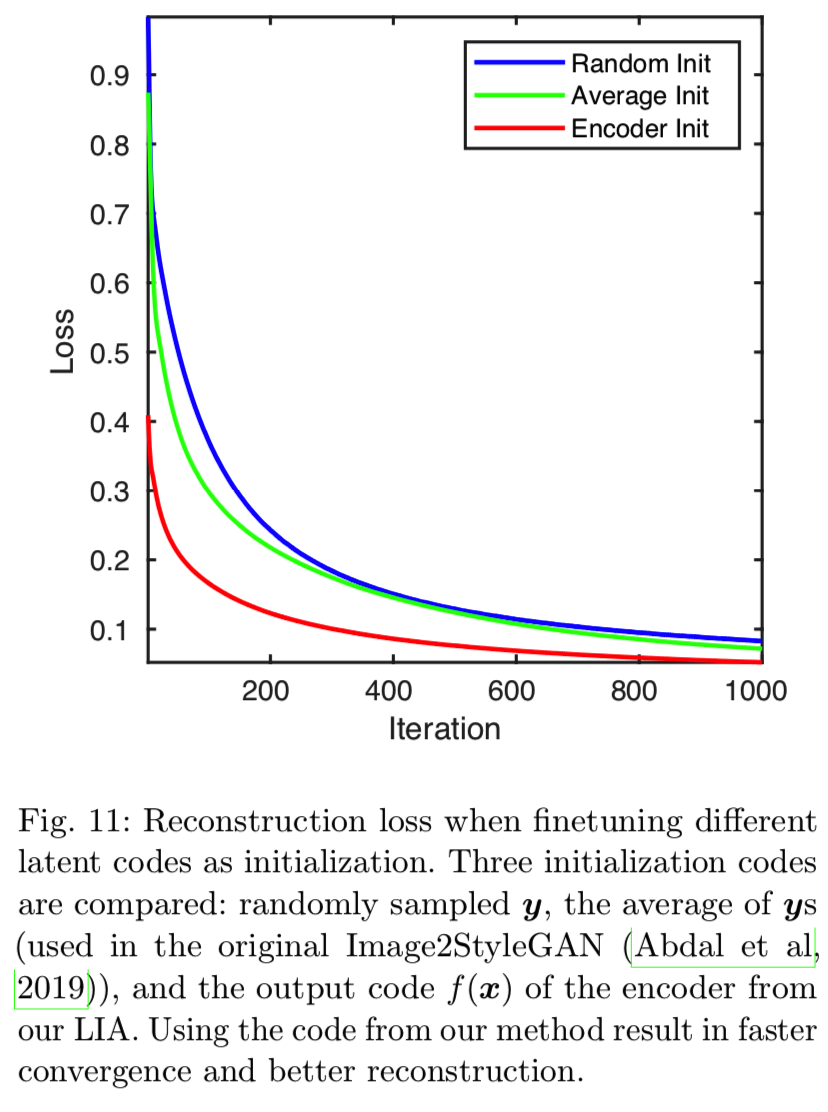
进一步提高重构精度的方法有两种:增加中间隐藏空间的维数和对模型进行微调以适应特定图像。较大的潜在空间可以保存更多的图像语义信息,而对图像进行微调可以恢复物体或场景的特定特征。Image2StyleGAN算法(Abdal et al, 2019)就是这样一个例子,该算法通过优化基于MSE的GAN反演,将不同的ys分配到StyleGAN生成器的不同层。不同的ys跨越一个高维潜在空间。正如第2节中分析的那样,GAN反演严重依赖于y的初始化,即使对于解耦的情况也是如此。原有的Image2StyleGAN方法采用y的平均值作为初始值来改善这一问题。为了说明该算法推理能力的优越性,我们比较了利用GAN反演进行模型微调的三种初始化情况:随机抽样、平均值和LIA编码器encoder的输出。关联优化是基于重构损失的:
![]()
其中,综合网络g已经被训练好了,并且在这里的反演过程中被frozen住,不进行更新。对于我们的方法,我们取y的初始值作为编码的潜在编码y0 = f(x)。
如图8所示,LIA重构的人脸是最好的。例如,Monnalisa右眼附近的发型可以从LIA的潜在代码中正确恢复,而Image2StyleGAN和随机抽样都失败了。图9对比了面部局部部位的详细重建质量。从图11所示的损失可以定量地验证LIA的一致性优势。

6.4 Disentanglement vs. Entanglement for GAN Inversion
为了进一步验证第2节中关于解耦和耦合的分析,我们也在上一节中对耦合z空间进行了实验。采用(13)中相同的GAN反演优化方法。对于z空间,三种算法的初始z0是通过可逆网络由y-to-z映射得到的,即z0 = Φ(y0)。即,三种算法在z空间和y空间的初始化中使用完全相同的初始重构,如图10中的第二行所示。从图10(c)和(d)可以看出,y空间的重构结果明显好于z空间。这三种算法都不能在z空间的正确极小值处收敛。一个有趣的观察是,对于随机初始化,反演算法能够在y空间中获得几乎正确的重构,而在z空间中,它完全不能为DiCaprio(即小李子)的情况生成有意义的脸。这说明变量的耦合会导致算法的收敛性变差。

6.5 Disentanglement Facilitates Optimization
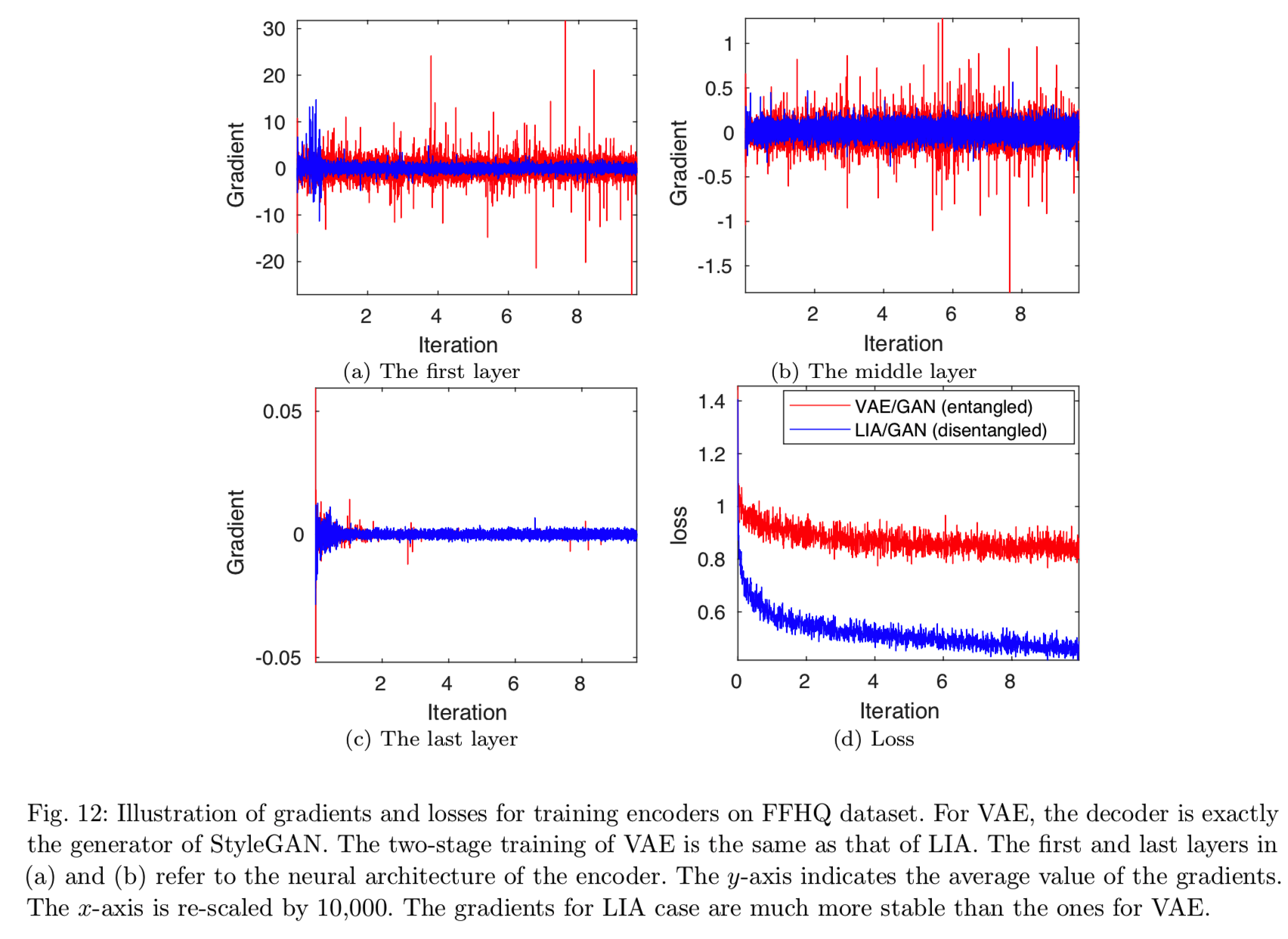
为了进一步揭示LIA中解纠缠的重要性,我们研究了两阶段训练中编码器学习编码器时,在两种不同的解码器情况下编码器的梯度。第一种情况是像VAE一样直接应用kl-散度来优化随机潜空间。编码器和解码器的映射是![]() ,其中
,其中![]() 是StyleGAN的映射网络(MLP) 。这是通过变分推理学习GAN算法编码器的传统方法。第二个是我们的LIA的架构,用于第二阶段的训练,即由于可逆网络的对称设计去除了潜在空间。图12清楚地说明了这两种情况下的梯度差异。用于变分推理的梯度波动率很高,而相关的损失没有得到有效的减少,这意味着训练过程中的梯度是有噪声的,并不总是有信息的。这可能表明,潜在空间中的耦合对通过变分推理训练编码器造成了问题。相反,编码器的梯度对于LIA在不同层之间是相当稳定的,并且损失单调下降,显示了通过可逆网络解耦训练的重要性。
是StyleGAN的映射网络(MLP) 。这是通过变分推理学习GAN算法编码器的传统方法。第二个是我们的LIA的架构,用于第二阶段的训练,即由于可逆网络的对称设计去除了潜在空间。图12清楚地说明了这两种情况下的梯度差异。用于变分推理的梯度波动率很高,而相关的损失没有得到有效的减少,这意味着训练过程中的梯度是有噪声的,并不总是有信息的。这可能表明,潜在空间中的耦合对通过变分推理训练编码器造成了问题。相反,编码器的梯度对于LIA在不同层之间是相当稳定的,并且损失单调下降,显示了通过可逆网络解耦训练的重要性。
7 Conclusion
提出了一种新的生成模型——隐可逆自编码器(Latently Invertible Autoencoder,LIA),该模型可以根据概率先验生成图像样本,同时对给定样本推断出精确的潜在编码。LIA的核心思想是在编码器中对称嵌入一个可逆网络。然后将神经结构作为两个分解模块进行对抗性学习训练。通过两阶段训练的设计,该解码器decoder可以替换为任何GAN发生器,实现高分辨率图像生成。可逆网络的作用是消除任何概率优化和将先验与展开的特征向量连接起来。通过对FFHQ和LSUN数据集进行重构(推理和生成)的实验,验证了该方法的有效性。通过LIA对潜在代码的精确推断,未来的工作将是促进基于GAN的模型的各种应用,例如图像编辑、数据增强、few-shot学习和3D图形。
总结:
其实这个论文的第一阶段其实就是训练得到一个styleGAN,z等价于styleGAN中的z(耦合的),y相当于styleGAN中的w(解耦的);第二阶段其实就是训练一个encoder,能够根据输入得到一个潜在编码y(即styleGAN解耦的w),然后将这个潜在编码最为styleGAN的w输入就能够很好地重构出这张图
它说明了训练一个encoder去得到一个解耦的w直接作为styleGAN的输入去重构图像的效果 是 比训练一个encoder去得到耦合的z,然后将其输入mapping网络中得到解耦的w,再去重构图像的效果是好很多的
所以想要做图像编辑,训练encoder或微调来得到潜在编码时,记得直接训练得到解耦的w编码效果会更好




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】博客园携手 AI 驱动开发工具商 Chat2DB 推出联合终身会员
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步