GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium（FID）- 1 - 论文学习

 

GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium

https://github.com/bioinf-jku/TTUR

 

Abstract

生成式对抗网络(GANs)擅长创建具有复杂模型的真实图像，这些模型是极大似然不可行的。然而，GAN训练的收敛性尚未得到证实。提出了一种用于训练任意GAN损失函数上具有随机梯度下降的GANs的双时间尺度更新规则(TTUR)。TTUR对于判别器和生成器都有单独的学习速率。利用随机*似理论，证明了TTUR在温和假设下收敛于一个*稳的局部纳什均衡。该收敛性延续到流行的Adam优化，为此我们证明了它遵循一个有摩擦的重球的动力学，因此在客观landscape中更倾向于*坦的最小值。为了评估GANs在图像生成中的性能,我们引入“Fréchet Inception Distance”(FID),能比Inception Score更好地捕获到真实图像和生成图像之间的相似度。在实验中，TTUR提高了DCGANs的学习能力，并改进了Wasserstein GANs (WGAN-GP)，使其在CelebA、CIFAR-10、SVHN、LSUN和One Billion Word的基准测试中优于传统的GAN训练。

 

Introduction

生成式对抗网络(GANs)[18]在生成逼真的图像[51、36、27、3、6]和生成文本[23]方面取得了显著的效果。GANs可以学习最大似然或变分*似不可行的复杂生成模型。判别器网络代替了似然，作为生成模型，即生成器的目标。GAN学习是生成器和判别器之间的博弈，生成器从随机变量中构造合成数据，判别器从真实数据中分离合成数据。生成器的目标是构造这样一种数据:判别器无法将它们与真实世界的数据区分开来。因此，判别器试图最小化合成-真实判别错误，而生成器试图最大化这个错误。由于训练GANs是一个博弈，其解是一个纳什均衡，梯度下降可能无法收敛[53,18,20]。由于梯度下降法是一种局部最优方法，因此只能得到局部纳什均衡。如果在参数空间中某一点附*存在一个局部邻域，且该邻域内的生成器和判别器都不能单方面地减少各自的损失，则称该点为局部纳什均衡。

如何描述训练的广义GANs网络的收敛性仍是一个有待解决的问题[19,20]。对于特殊的GAN变体，在一定的假设条件下可以证明其收敛性[39,22,56]。许多收敛证明的前提是局部稳定性[35]，Nagarajan和Kolter[46]给出了GANs的最小最大GAN设置。然而，Nagarajan和Kolter要求他们的证明要么是非常强的和不切实际的假设，要么是对线性判别器的限制。最*的GANs收敛证明对训练样本的期望成立，或者需要无限多的样本条件成立[37,45,40,4]，因此不考虑导致随机梯度的小批量学习的情况[57,25,42,38]。

*年来，人们开始使用随机*似的方法来分析 actor-critic 学习。Prasad等人的[50]表明，如果批评者学习速度比行动者快，则双时间尺度的更新规则可以确保训练达到稳定的局部纳什均衡。用常微分方程(ODE)证明了收敛性，其稳定极限点与*稳局部纳什均衡一致。我们遵循同样的方法。证明了在双时间尺度更新规则(TTUR)训练下，即当判别器和生成器有不同的学习率时，GANs网络收敛于局部纳什均衡。这也导致了更好的实验结果。主要的前提是，判别器收敛到一个局部最小值时，生成器是固定的。如果生成器的变化足够慢，那么判别器仍然收敛，因为生成器的扰动很小。除了确保收敛，性能也可能提高，因为判别器必须首先学习新的模式，然后才转移到生成器。与此相反，一个过于快速的生成器，可以稳定地驱动判别器进入新的区域，而不需要捕获它收集到的信息。在最*的GAN实现中，判别器通常比生成器学得快。一个新的目标减慢了生成器，以防止它在当前的判别器[53]上过度训练。Wasserstein GAN算法对判别器使用的更新步骤比生成器[3]更多。我们比较了TTUR和标准GAN训练。图1显示了一个在CelebA上的原始GAN训练(orig)的随机梯度示例，该示例经常导致振荡；以及TTUR示例。在右边的面板上显示了Zhang等人[61]的一个4节点网络流问题的例子。实际参数与在单时间尺度更新规则中的最优值之间的距离迭代显示：

当误差的上界很小时，迭代会返回到最优解的邻域，而对于较大的误差，迭代可能会发散(参见附录部分A2.3)。

在该论文中我们的贡献是：

• 用于GANs的双时间尺度更新规则
• 证明用TTUR训练的GANs收敛于*稳局部纳什均衡
• Adam被描述为带摩擦重球及其结果为二阶微分方程
• 使用TTUR和Adam训练的GANs收敛于*稳局部纳什均衡
• 介绍了“Fréchet Inception Distance” (FID)去评估GANs，比Inception Score更好

 

Two Time-Scale Update Rule for GANs

判别器为参数为ω的D(.;ω),生成器维参数为Θ的G(.;Θ)。学习是基于判别器损失函数L_D的随机梯度和生成器损失函数L_G的随机梯度。损失函数L_D和L_G可以是如Goodfellow et al. [18]介绍的原始版本，也可以是改善版本[20]或最*提出的损失如Wasserstein GAN[3]。我们的设置没有局限于min-max，适用于所有其他版本，如更通用的判别器的损失函数L_D不需要与生成器的损失函数L_G相关的GANs。梯度和是随机的，因此他们使用mini-batches为m个随机选择的真实样本和m个随机选择的生成样本。如果真实梯度为和，那么就能使用随机变量定义。因此梯度和随机*似于真实梯度。因此，我们用双时间尺度的随机*似算法来分析GANs的收敛性。对于双时间尺度更新规则（TTUR），我们分别设置判别器和生成器更新的学习速率为b(n)和a(n)：

 

有关以下收敛性证明及其假设的更多详细信息，请参见附录A2.1节。为了证明TTUR所学习的GANs的收敛性，我们做了如下假设（实际假设以表示结束，剩下文本只是评论和解释）：

• （A1）梯度h和g是Lipschitz。因此带有 Lipschitz*滑激活函数，如ELUs(=1)[13]的网络履行了假设，带有ReLU的网络没有履行该假设
• （A2）
•  （A3）随机梯度误差是鞅差序列（martingale difference sequences）

其中B1和B2是正的确定的常数1997年Borkar 的原始假设(A3)来自于[7]中的引理2(也见[52])。这一假设在Robbins-Monro设置中得到了实现，其中小批量被随机取样，梯度是有界的。

• （A4）对每个Θ，ODE 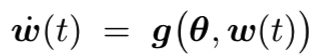在吸引域G_Θ内有局部渐*稳定attractor λ(θ),其中λ是Lipschitz。ODE 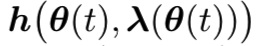在吸引域内有局部渐*稳定attractor θ^*。 对固定生成器参数和生成器。判别器必须收敛到一个最小值；反过来，对该固定的判别器，生成器必须收敛到一个最小值。Borkar 1997需要唯一的全局渐*稳定*衡[9]。在Karmakar和Bhatnagar[28]中，通过假设(A6)和定理2.7将全局attractors的假设放宽为局部attractors。详见附录A2.1.3部分的假设(A6)。在这里，GAN的目标可以作为Lyapunov函数。局部稳定ODE的这些假设可以通过在损失函数中增加一个额外的权值衰减项来保证，该权值衰减项增加了Hessian的特征值。从而避免了二阶导数为零的区域常数判别器的问题。有关进一步讨论，请参见附录A2 (C3)节。
• （A5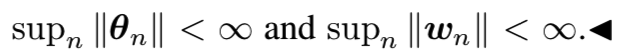）通常由目标函数或权重衰减项保证

 下一个定理已经在Borkar 1997年的开创性论文[9]中得到了证明。

 

 Theorem 1 (Borkar).如果满足假设，更新等式(1)收敛于 (θ^∗, λ(θ^∗)) a.s.

当θ^∗和λ(θ^∗)是满足的局部渐*的稳定attractor时，(θ^∗, λ(θ^∗))是*稳的局部纳什均衡[50]。使用泊松方程证明收敛性的另一种方法可在附录A 2.1.2中找到，该方法用于确保快速更新规则的解。该方法假设在快速更新规则中存在一个线性更新函数，但该函数可以是非线性梯度的线性*似[30,32]。收敛速度见附录A2.2部分，其中A2.2.1部分侧重于线性更新，A2.2.2部分侧重于非线性更新。对于相同的时间尺度，只能证明更新会无限频繁地重新访问解决方案的环境，但是，这个环境可能非常大[61,14]。关于相同的时间尺度的分析的更多细节见附录A2.3节。Borkar证明的主要想法[9]是根据1989年Hirsch[24]使用(T,δ)干扰ODEs(see also Appendix Section C of Bhatnagar, Prasad, & Prashanth 2013 [8])。证明依赖于当缓慢更新规则足够小时(由δ给定) ，最终会有一个时间点允许快速更新规则收敛的事实。对于TTUR的实验，我们的目标是找到这样的学习率使得缓慢更新足够小以允许快速更新收敛。通常，缓慢更新是生成器，快速更新是判别器。我们必须调整这两个学习速率，使生成器不会以不希望的方式影响判别器的学习，并对其产生过多的干扰。然而，即使发生器的学习率比判别器的学习率大，也能保证判别器有小的干扰。由于来自生成器的判别器的干扰与来自判别器的生成器的干扰是不同的，所以学习率不能直接转化为干扰。

 

Adam Follows an HBF ODE and Ensures TTUR Convergence

在我们的实验中，我们的目标是使用Adam随机*似来避免模式崩溃。GANs遭受“模式崩溃”，在这种情况下，大量的概率被映射到少数几个只覆盖小区域的模式上。虽然这些区域代表有意义的样本，但是真实世界数据的多样性丢失了，只生成了很少的原型样本。已经提出了不同的方法来避免模式崩溃[11,43]。我们用Adam随机*似[29]来避免模式崩溃。Adam可以被描述为带有摩擦的重球(Heavy Ball with Friction ，HBF)(见下文)，因为它是过去梯度的*均值。这种*均对应的速度使生成器难以被推到小区域。Adam作为一种典型的HBF方法，它超越了与模式崩溃相对应的局部极小值，并能找到[26]的*坦极小值。图2描述了HBF的动力学，其中球稳定在一个*坦的最小值：

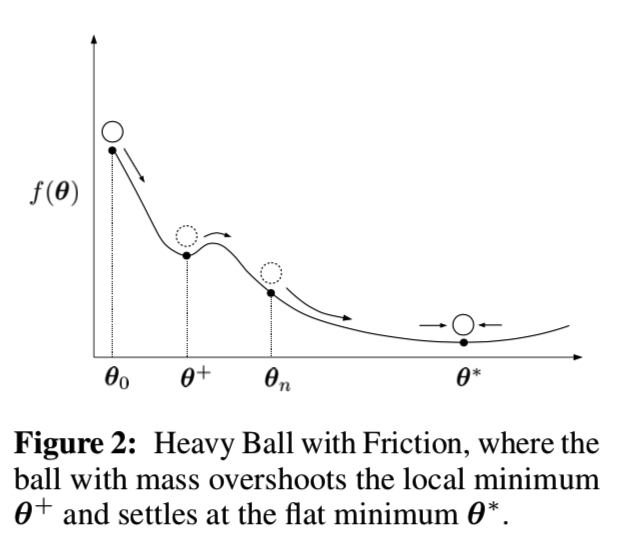
接下来，我们分析了在使用Adam时，使用TTUR训练的GANs是否收敛。更多细节见附录A3部分。

我们概括了Adam在n步时的带有学习率α的更新规则、第一指数*均因子β₁和梯度∇f(θ_n−1)二阶矩的指数*均因子β₂:

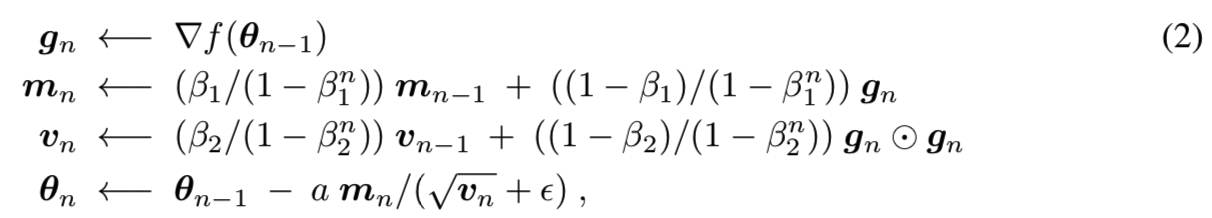
其中下列操作是meant componentwise:内积⊙，*方根√., 和最后一行的除法/。相比学习率α,我们介绍了a(n) =an^−τ，其中τ∈(0,1)的阻尼系数a(n)。Adam有用于*均梯度的参数β₁和用于*均*方梯度的被一个正数α参数化的参数β₂。这些参数可以被认为是为Adam定义了一个内存。为了在下面描述β₁和β₂,我们定义了用于正常数r的指数内存r(n) = r和多项式内存。下一个定理描述了Adam的微分方程,进而可以使用(T,δ)干扰ODEs的想法到TTUR中。因此，用TTUR和Adam学习GANs是收敛的。

 

定理2. 如果Adam带有β₁ = 1−α(n + 1)r(n), β₂ = 1−αa(n + 1)r(n)和∇f作为梯度的下界,以及连续可微的目标f,那么为了稳定的梯度的二阶矩,Adam遵循Heavy Ball with Friction(HBF)的微分方程:

 

证明. Gadat等人推导出了Polyak的Heavy Ball method[49]，即Heavy Ball with Friction(HBF)[17]的离散随机版本:

这些更新规则是Adam[29]的第一次更新规则。HBF可以表示为等式(3)[17]的微分方程。Gadat et al. 表明,等式(4)的更新规则收敛于有着最多二次增长的损失函数f, 声明收敛可被L-Lipschitz [17]的∇f 证明。证明了连续可微的凸函数f的收敛性(Theorem 3 in Goudou & Munier [21])。证明了L-Lipschitz的∇f的收敛性和其下界(Theorem 3.1 in Attouch et al. [5])。Adam用梯度g_n的二阶矩v_n将*均m_n归一化:v_n = E [g_n⊙g_n]。m_n在分量上除以v_n分量的*方根。我们假设g_n的二阶矩是*稳的，即，v = E [g_n⊙g_n]。在这种情况下，归一化可以看作是附加噪声，因为归一化因子随机偏离其均值。在HBF解释中，√v归一化相当于引入引力。我们获得：

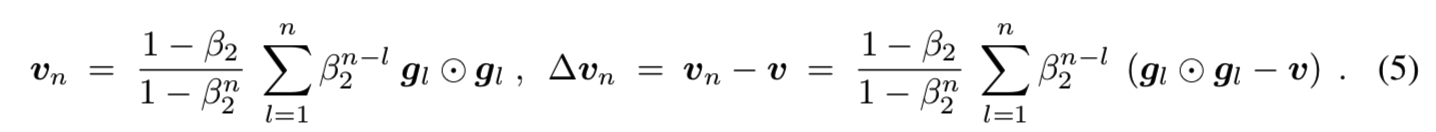
对于稳定二阶矩v和β₂ = 1−αa(n + 1)r(n)，我们有。我们使用componentwise线性*似到Adam的二阶矩归一化，其中所有操作是meant componentwise。如果我们设置 。对于稳定的二阶矩v，随机变量是一个带有边界二阶矩的鞅差序列。因此能在更新规则等式(4)被纳入。该方法在不改变最小值的情况下，将因子1/√v按分量合并到梯度g中。

 

根据Attouch et al. [5] 的energy,即一个Lyapunov函数和自从Adam可以表示为微分方程和Lyapunov函数,(T,δ)扰动ODEs[9,24,10]的思想被带到了Adam。因此，可以通过类似Borkar [9] 中用于梯度稳定二阶矩的双时间尺度的随机*似分析来证明Adam与TTUR的收敛性。

 

在附录中，我们进一步讨论了两种具有附加噪声、基于马尔可夫链的线性更新函数，基于非线性更新函数，以及基于受控马尔可夫过程的更新的双时间尺度的随机*似算法的收敛性。此外，附录还介绍了线性和非线性更新规则的收敛速度，使用类似于Nagarajan和Kolter[46]的局部稳定性分析的技术。最后，我们对等时间尺度更新做了进一步的阐述，研究了鞍点问题和actor-critic学习。

 

简单说来，什么是TTUR：

在优化G 的时候，我们默认是假定我们的 D 的判别能力是比当前的 G 的生成能力要好的，这样 D 才能指导 G 朝更好的方向学习。通常的做法是先更新 D 的参数一次或者多次，然后再更新 G 的参数，TTUR 提出了一个更简单的更新策略，即分别为 D 和 G 设置不同的学习率，让 D 收敛速度更快。即一般将判别器的学习率设置得比生成器的学习率大

 

Experiments

Performance Measure. 在介绍实验之前，我们介绍了一个由GANs学习用于模型的质量度量方法。生成学习的目标是生成与观测数据相匹配的数据。因此，观察真实世界数据p_w(.)的概率与生成模型数据p(.)的概率之间的每一个距离都可以作为生成模型的性能度量。然而，为生成模型定义适当的性能度量是困难的。最著名的测量方法是似然法，它可以通过对重要抽样[59]的退火来估计。然而，似然很大程度上取决于真实数据的噪声假设，并且可能由单个样本[55]决定。其他方法，如密度估计，也有缺点[55]。度量GANs性能的一种良好的方法是“Inception Score”，它与人类的判断[53]相关。生成的样本被输入到在ImageNet上训练的inception模型中。具有有意义的对象的图像应该具有较低的标记(输出)熵，即它们属于较少的对象类。另一方面，图像之间的熵应该很大，即图像之间的方差应该很大。Inception分数的缺点是没有使用真实世界样本的统计数据，也没有与合成样本的统计数据进行比较。接下来，我们将改进Inception Score。对于一个基f(.)，它跨越了p(.)和p_w(.)所在的函数空间，当且仅当是一个不可测集时，等式p(.) = p_w(.)成立。这些期望的等式用于描述矩或累积量的分布，其中f(x)是数据x的多项式。我们通过inception模型的编码层（即图像的分类输出之前的最后池化层）替换x来概括这些多项式，以获得与视觉相关的特征。由于实际原因，我们只考虑前两个多项式，即前两个矩:均值和协方差。高斯分布是给定均值和协方差的最大熵分布，因此我们假设编码单元服从一个多维高斯分布。两个高斯分布的差异(合成和真实图像)被Fréchet距离[16][58]也称为Wasserstein-2距离衡量。我们称从p(.)获得的均值、协方差为(m,C)的高斯分布 和从p_w(.)获得的均值、协方差为(m_w, C_w)的高斯分布之间的Fréchet距离d (.,.)为“Fréchet Inception Distance”(FID),由[15]提供:

 

其中Tr表示矩阵的迹（矩阵对角元之和）

如果FID值越小，则相似程度越高。最好情况即是FID=0，两个图像相同。

FID值越小说明模型效果越好

 

接下来，我们证明了FID与不断增加的干扰和人类的判断是一致的。图3对FID进行了评估，包括高斯噪声、高斯模糊、植入的黑色矩形、漩涡图像、盐和胡椒噪声，以及受到ImageNet图像污染的CelebA数据集：

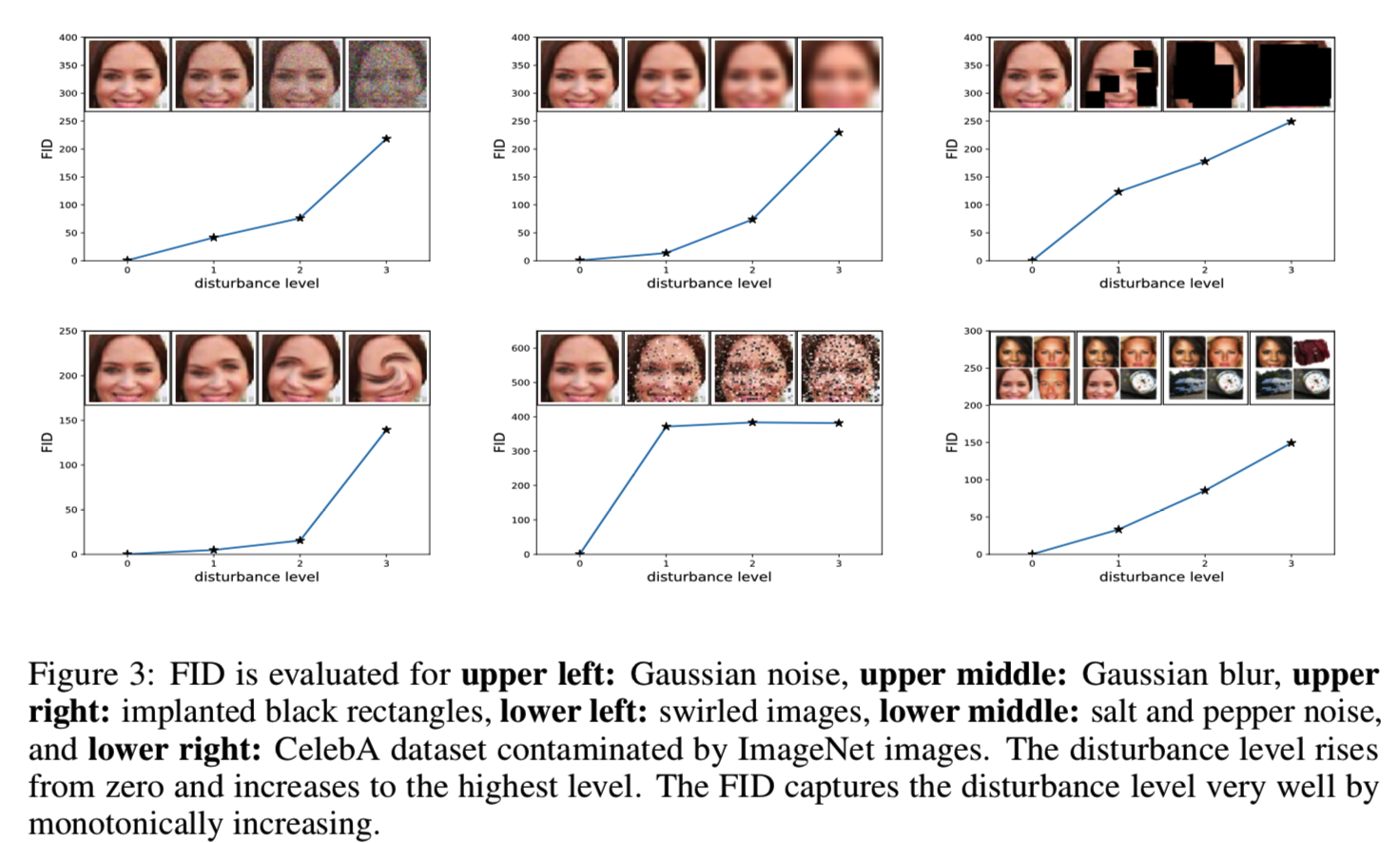
FID很好地捕捉到了扰动水*。在实验中，我们使用FID来评估GANs的性能。要了解更多的细节，以及FID和Inception分数的比较，请参见附录A1部分，我们在这里展示了FID比Inception分数更符合噪音水*。

 

总结FID计算方式：

• 将合成图像输入Inception模型中，取其最后池化层的输出来计算均值和协方差(m,C)
• 同样将真实图像输入Inception模型中，取其最后池化层的输出来计算均值和协方差(m_w, C_w)
• 然后根据上面的式子计算Fréchet距离d (.,.)，就得到了“Fréchet Inception Distance”(FID)的结果

 

Model Selection and Evaluation.  我们将GANs的双时间尺度更新规则(TTUR)与原始的GAN训练进行比较，看看TTUR是否提高了GANs的收敛速度和性能。我们选择Adam随机优化来降低模式崩溃的风险。Adam的优势已经被MNIST实验证实，在那里Adam确实大大减少了我们观察到的模式崩溃的情况。虽然TTUR保证了判别器在学习过程中是收敛的，但是每个实验都必须找到可行的学习速率。我们面临一个权衡，因为学习速率应该足够小(例如对于生成器)，以确保收敛，但同时又应该足够大，以允许快速学习。对于每一个实验，学习率已经被优化为很大，同时仍然确保稳定的训练，这是由减少FID或Jensen-Shannon散度(JSD)表示的。我们进一步确定了当最优模型的FID或Jensen-Shannon散度不再减小时，停止训练的时间点为更新步长。对于某些模型，我们观察到FID在某个时间点发散或开始增加。这种行为的一个例子如图5所示：

 

 

 生成模型的性能通过上面介绍的Fréchet初始距离(FID)评估。对于 One Billion Word 实验，规范化的JSD作为性能度量。为了计算FID，我们在Inception Score[53]的计算之后，通过预训练的inception-v3模型传播来自训练数据集的所有图像，但是，我们使用最后一个池化层作为编码层。对于这一编码层，我们计算了均值m_w和协方差矩阵C_w。因此，我们在真实世界分布下*似Inception编码层给出的函数的第一和第二中心矩。为了*似模型分布的这些矩,我们生成50000张图片,传播到Inception-v3模型,然后计算均值m和协方差矩阵C。为计算效率,我们对每1000个DCGAN mini-batch更新、用于图像实验的每5000个WGAN-GP外层迭代,和用于WGAN-GP语言模型的每100个外层迭代评估FID。对于单时间尺度，遵循原始实现，更新一个由5个判别器mini-batch组成的图像模型和 由10个用于语言模型的判别器mini-batch的WGAN-GP外部迭代。但是对于TTUR，判别器每次迭代只更新一次。我们对每个单一时间尺度(orig)和TTUR学习率重复训练8次，对图像数据集重复训练10次，对语言基准测试重复训练10次。除了*均FID训练进度之外，我们还展示了在每个评估时间步长上所有运行的最小FID和最大FID。有关更多细节、实现和进一步结果，请参见附录A4和A6部分。 

 

Simple Toy Data.  我们首先要演示在一个简单的toy最小/最大问题中单时间尺度的更新规则和TTUR之间的区别，该问题应该找到一个鞍点。如图4（left）的目标函数在(x,y) = (0,0)有一个鞍点，满足假设A4。范数||(x, y)||测量参数向量(x, y)到鞍点的距离。我们通过x的梯度下降和y的梯度上升更新(x, y)，使用额外高斯噪声来模拟随机更新。更新应该收敛于鞍点(x, y) =(0,0)，目标值f(0,0) = 100，范数为0。在图4(右)中，前两行显示单时间尺度更新规则。第一行的大学习率是发散的，有较大的波动。第二行的学习率较小，但收敛速度慢于第三行的TTUR，第三行的x更新速度较慢。第四行中y更新慢的TTUR也收敛，但速度较慢。

 

 

 可见第三行设置x的学习率为0.0001，y的学习率为0.01时效果最好，目标函数f(0,0)很快为100，范数||(x, y)||很快为0.

 

DCGAN on Image Data.  我们在CelebA、CIFAR-10、SVHN和LSUN Bedrooms数据集上为深度卷积GAN (DCGAN)[51]测试了TTUR。图5显示了使用原始学习方法(orig)和TTUR学习时的FID：

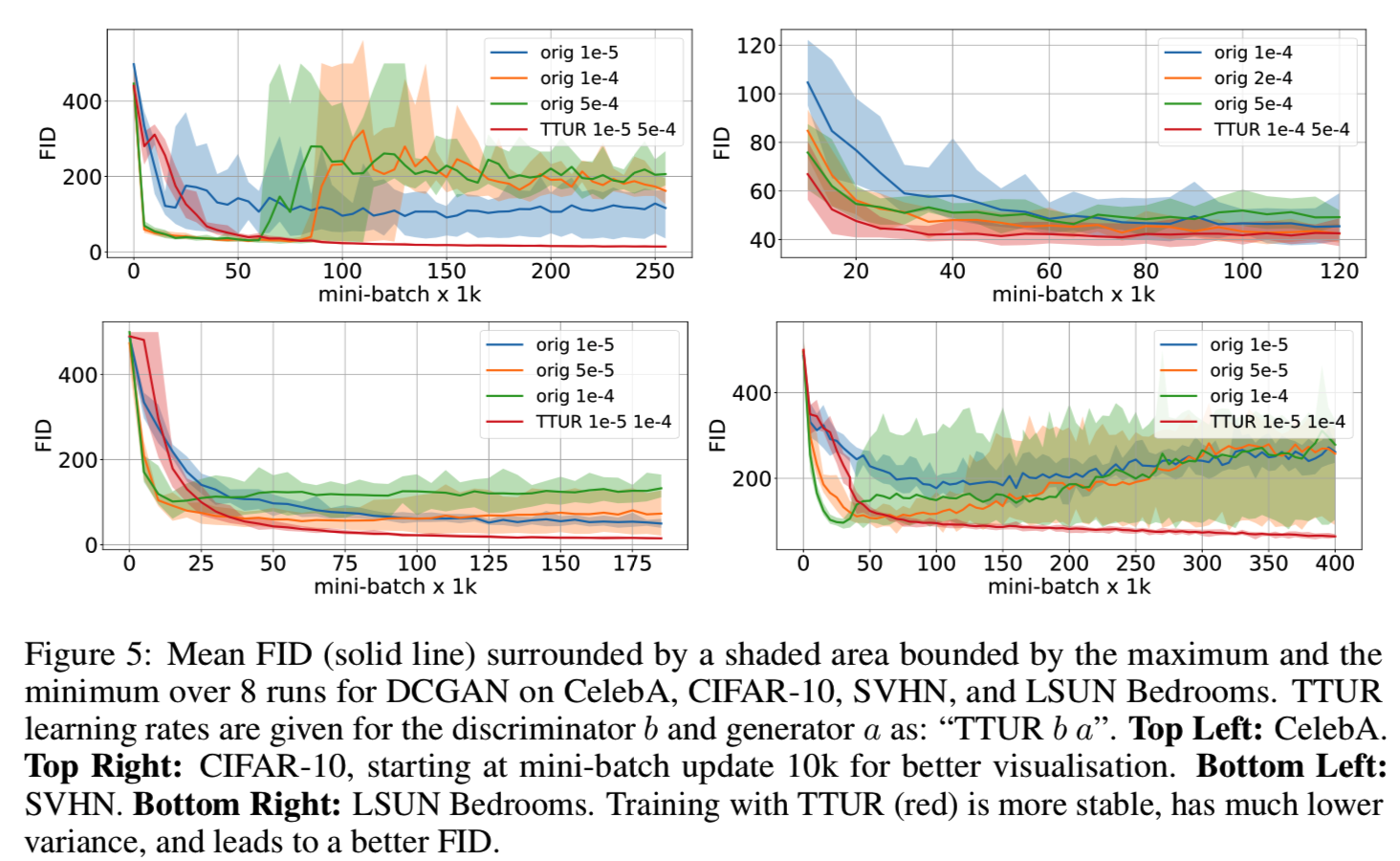
最初的训练方法速度较快，但TTUR最终取得了较好的成绩。DCGAN训练的TTUR的FID值始终低于原来的方法，而CelebA和LSUN Bedrooms的时间尺度都是发散的。对于DCGAN，生成器的学习率大于判别器的学习率，但这与TTUR理论并不矛盾(见附录A5)。在表1中，我们报告了使用TTUR的最佳FID和单时间尺度训练针对优化的更新次数和学习率。TTUR不断超越标准训练，更加稳定。

 

 

 

WGAN-GP on Image Data.  我们使用WGAN-GP图像模型[23]来测试使用CIFAR-10和LSUN Bedrooms数据集的TTUR。与原始代码中判别器每训练五次，生成器更新一次不同，TTUR只更新判别器一次（即判别器更新一次，生成器更新一次），因此我们将训练进度与wall-clock时间保持一致。原始训练的学习率优化为较大的值，但学习稳定。由于TTUR能够稳定学习，因此可以使用更高的判别器学习率。图6显示了使用原始学习方法和TTUR学习时的FID：

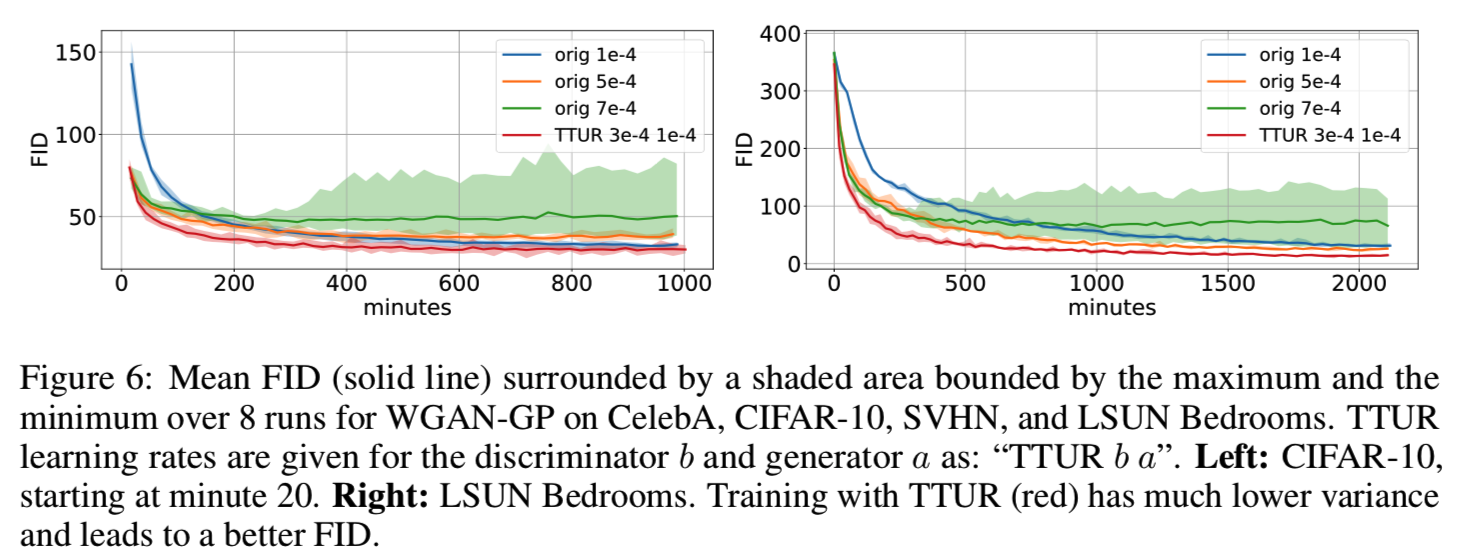
表1显示了带有TTUR的最佳FID，以及单时间尺度训练用于优化的迭代次数和学习率。再次，TTUR达到比单时间尺度训练更低的FIDs。

 

WGAN-GP on Language Data.  最后，用One Billion Word基准[12]对WGAN-GP上的TTUR进行了评价。字符级生成语言模型是一个一维卷积神经网络(CNN)，它将一个潜在向量映射到一个由softmax输出的最大值所给出的32维的one-hot字符向量序列。判别器也是一个应用于32个字符的one-hot向量序列的一维CNN。因为FID标准只适用于图像，所以我们使用Jensen-Shannon-散度(JSD)来测量模型和真实世界分布之间的性能，就像以前使用[23]所做的那样。与原始代码中训练10次更新一次生成器不同，TTUR只更新判别器一次，因此我们将训练进度与壁钟时间保持一致。原始训练的学习率优化为较大的值，但学习稳定。由于TTUR能够稳定学习，因此可以使用更高的判别器学习率。我们在图7中报告了原始训练和TTUR训练10次的归一化*均JSD值：

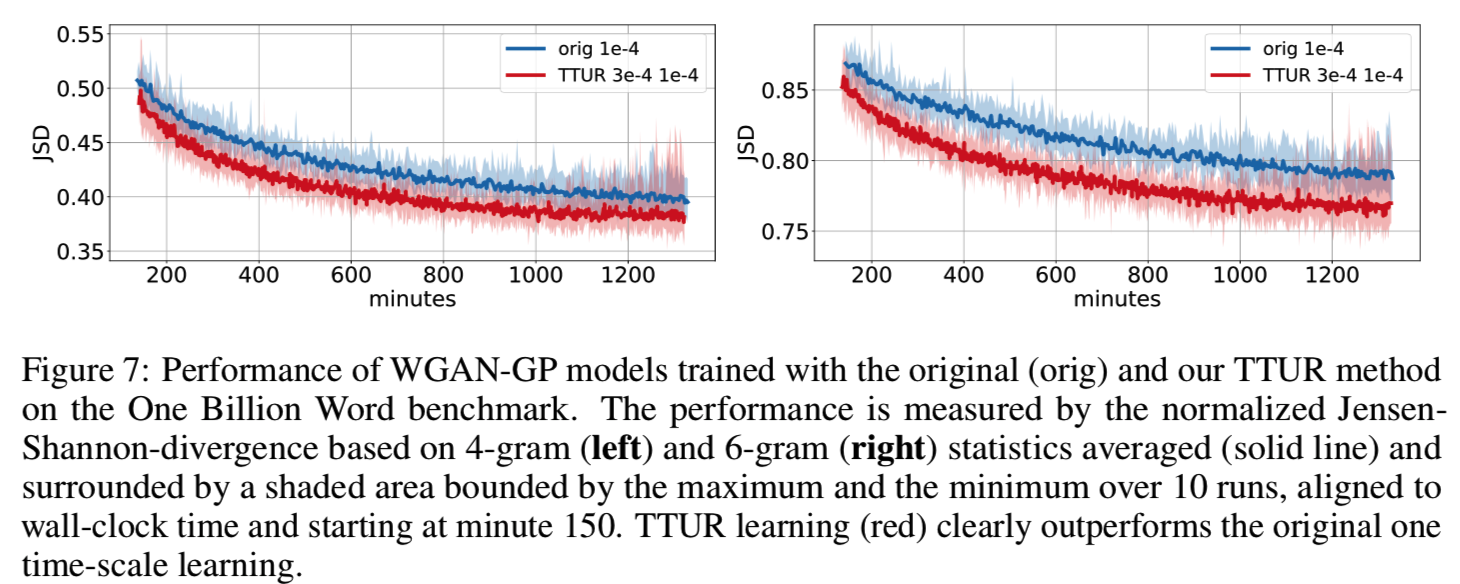
在表1中，我们报告了在最佳时间步长的最佳JSD, TTUR在这两种方法中都优于标准训练。与原始训练相比，TTUR对6-gram统计量的改进表明，TTUR能够学习生成更微妙的伪词，这些伪词更接*真实的单词。

 

 

Conclusion

在学习GANs神经网络时，我们引入了双时间尺度更新规则(TTUR)，并证明了该规则收敛于一个*稳的局部纳什均衡。然后，我们将Adam随机优化描述为一个带有摩擦的重球(HBF)动力学，这表明Adam收敛，Adam倾向于找到*坦的最小值，同时避免了小的局部最小值。二阶微分方程将Adam的学习动力学描述为一个HBF系统。通过该微分方程，可以将用TTUR训练的GANs收敛到一个*稳的局部纳什均衡，推广到Adam。最后,评估GANs,我们引入了“Fréchet Inception Distance”(FID),能比Inception Score更好地捕获到真实图像和生成图像之间的相似度。在实验中，我们在CelebA、CIFAR-10、SVHN、LSUN Bedrooms和One Billion Word的基准上将使用TTUR训练的GANs系统与使用单时间尺度更新规则的传统GANs训练进行了比较。TTUR在所有实验中均优于常规GAN训练。

 

 

附录

A1 Fréchet Inception Distance (FID)

...和Experiment-Performance Measure.中说的一样

接下来，我们证明FID在不断增加的干扰上和人类对CelebA数据集的判断是一致的。我们计算了所有的CelebA图像的(m_w, C_w)；而对于计算(m, C)，我们使用了50,000个随机选择的样本。我们考虑如下图像X的干扰（下面就是将怎么增加干扰项的）:

 

 

我们比较了Inception Score[53]和FID。m个样本和K个类的Inception Score是：

 

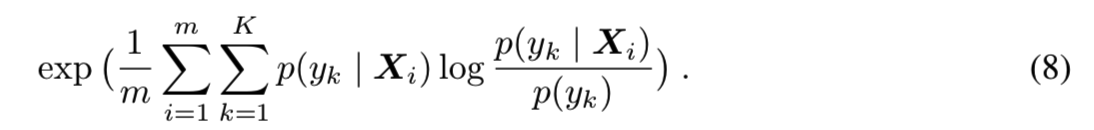
FID是一个距离，而Inception Score是一个分数。为了比较FID和Inception Score，我们将Inception Score转换为一个距离，我们称之为“Inception Distance”(IND)。这种到距离的转换是可能的，因为Inception Score有一个最大的值。对于0概率，设置值。可以得到log项的边界为：

 

 

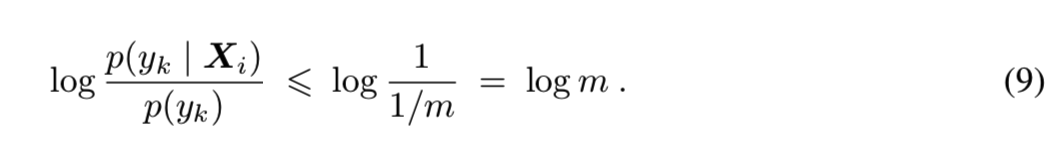
使用该边界，得到Inception Score的最大边界：

 

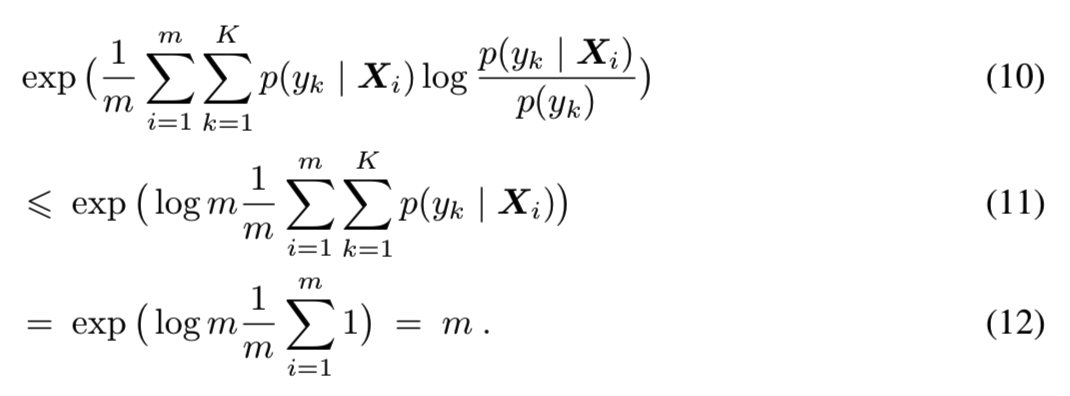
该上界是紧的,当m<=K能得到该上界，其中的每个样本来自不同的类，样本正确分类的概率为1。IND被计算为“IND = m - Inception Score”，因此对于ImageNet的一个完美子集m < K个样本，其中每个样本来自不同的类，IND为0。因此，随着扰动水*的增大，两种距离均应增大。在图A8中，我们给出了每种扰动的评估。扰动水*越大，FID和IND值越大：

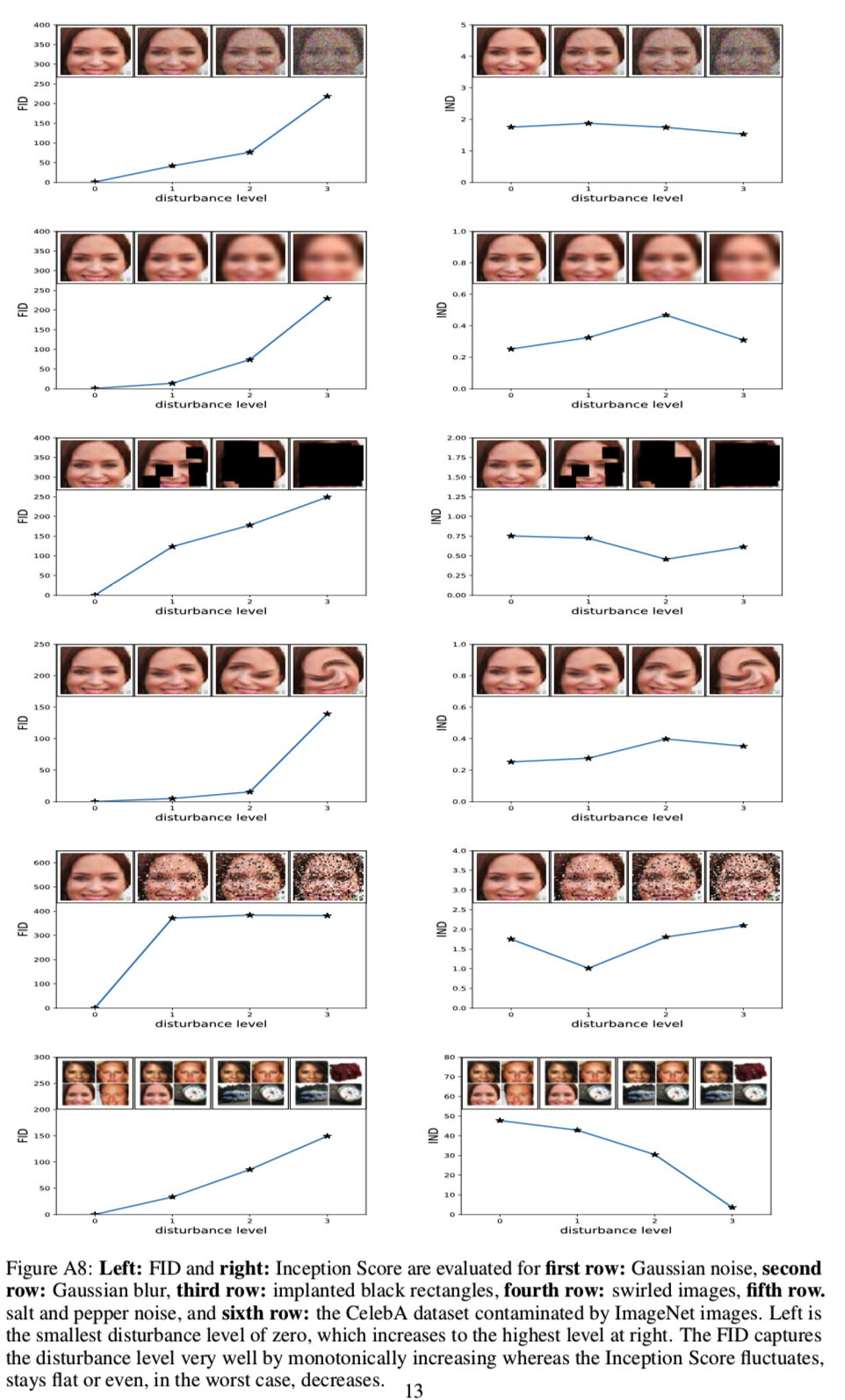
在图A9、A10、A11和A11中，我们展示了DCGAN在CelebA上使用FIDs 500、300、133、100、45、13进行训练生成的图像示例，以及使用WGAN-GP在CelebA上实现的FID 3。 

 

 

 

 

 

 

 

 

 

 

 

A2 Two Time-Scale Stochastic Approximation Algorithms

随机*似算法是一种迭代过程，它在只提供函数值或其导数的噪声观测的情况下，求出函数的根或驻点(最小、最大、鞍点)。双时间尺度随机*似算法是两种步长不同的耦合迭代。为了证明这些相互交织的迭代的收敛性，我们假设其中一个步长比另一个小得多。较慢的迭代(步长较小的迭代)被认为足够慢，从而允许快的迭代收敛，同时其又被较慢的迭代所困扰。慢速的扰动应该足够小，以保证快速的收敛。

在时间步长n>=0,迭代映射快速变量和慢速变量到他们的新值：

 

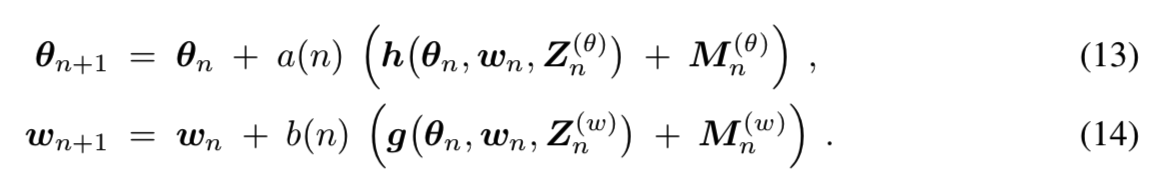
 迭代使用：

 

 

A2.1 Convergence of Two Time-Scale Stochastic Approximation Algorithms

A2.1.1 Additive Noise

第一个结果来自Borkar 1997年的[9]，它在Konda和Borkar 1999年的[31]中得到了推广。Borkar认为迭代为:

 

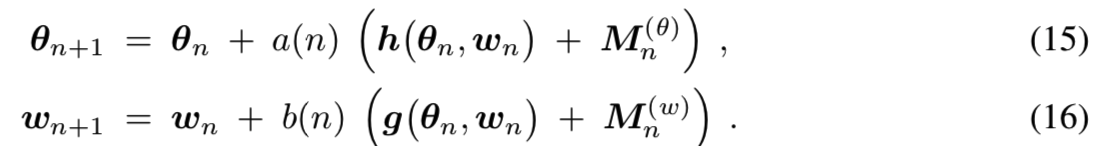
Assumptions. 有以下假设：

（A1）更新函数的假设：函数是Lipschitz

（A2）学习率的假设：

 

 

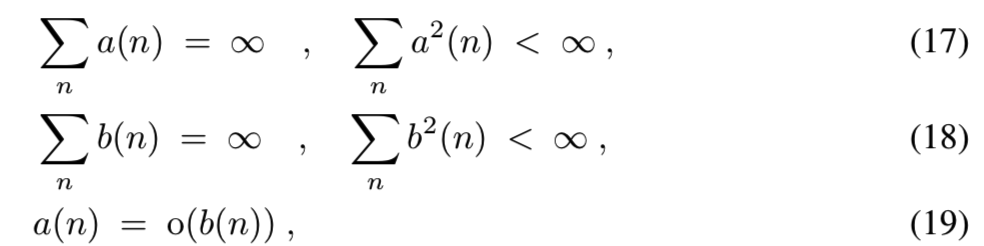
 （A3）噪音的假设：为增加σ-field：

 

 （A4）快速迭代解决方案存在的假设：对于每个：

 

（A5）缓慢迭代解决方案存在的假设：ODE

 

 （A6）边界迭代的假设：

 

 

收敛性定理(Convergence Theorem). 下一个定理来自Borkar 1997[9]。

定理3(Borkar). 如果假设满足,那么迭代等式(15)和等式(16)，将收敛于(θ∗,λ(θ)∗) a.s.

Comments

 （C1）

 

 

（C2）对于最常见的随机梯度情况——即小批量(mini-batch)学习，假设(A3)成立。

 

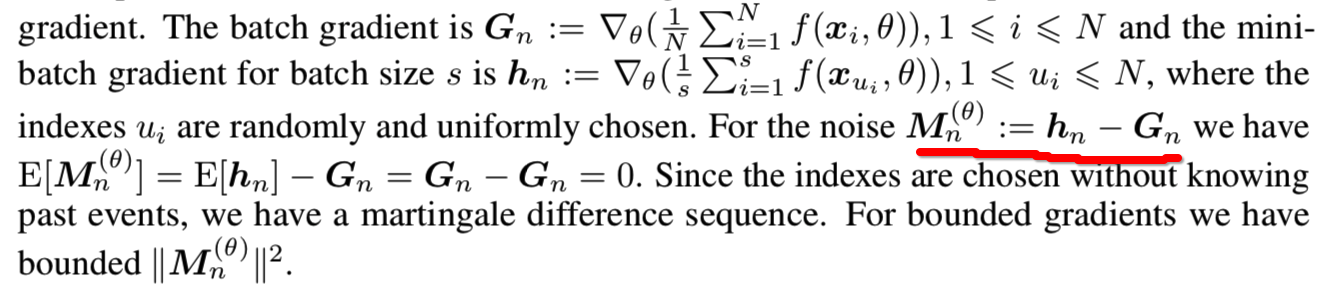
 （C3）我们用两种方法处理了带有权值衰减的假设(A4):(I)权值衰减避免了带有区域常数的判别器的问题，因此，没有一个局部稳定的生成器。如果生成器是完美的，那么判别器就是0.5。对于带模式崩溃的生成器，(i)在没有生成器实例的区域中判别器为1，(ii)在只有生成器实例的区域中判别器为0，(iii)等于带有生成器实例的区域与真实世界实例的局部比率。由于判别器是局部恒定的，所以生成器的梯度为零，不能进行改进。此外，判别器不能改善，因为对给定的生成器，它有最小的误差。然而，如果没有重量衰减，纳什均衡就不稳定，因为二阶导数也是零。(II)重量衰减避免了生成器被无界权值驱动到无穷大。例如，一个线性判别器可以为每一个有界区域外的生成器提供一个梯度。

(C4) 根据Hirsch 1989[24]，用于定理证明的主要结果依赖于ODE的扰动。
(C5) Konda和Borkar 1999[31]将收敛证明推广到分布式异步更新规则。
(C6) Tadic 放松的假设显示收敛[54]。特别地，噪声假设([54]中的假设A2)不必是鞅差序列，而且比[9]中的更一般。在另一个结果中，如果保证了其他的假设[54]，那么有界迭代的假设就没有必要了。最后,Tadic考虑了非附加噪声[54]的例子。Tadic不提供其结果的证明。我们甚至不能在Tadic的其他出版物中找到这样的证明。

 

不弄了太多了！！！！