LBP(Local Binary Pattern,局部二值模式)学习
参考http://blog.csdn.net/xidianzhimeng/article/details/19634573
https://wenku.baidu.com/view/d03494a687c24028905fc34b.html
LBP指局部二值模式,英文全称:Local Binary Pattern,是一种用来描述图像局部特征的算子,LBP特征具有灰度不变性和旋转不变性等显著优点
LBP是一种图像纹理特征提取算法,是一种局部特征,是照片分类和人脸检索研究中采用较多的特征提取算法之一。在图像物体识别领域,常用的特征描述子包括:HOG、SIFT、SURT、Wavelet、Gabor、DCT等,具体选择哪种算子需要根据目标对象决定。人脸识别中,LBP和Gabor是效果较好的两组特征。gabor效果比LBP效果鲁棒,但是LBP运算速度快,编译在嵌入式等平台运行。一般如果条件允许,二者会进行结合,包括定义结合特征(比如LGBP,LGXP等),特征级融合和决策级融合。
特征提取是希望将资料中重要的资讯提取出来,去除杂讯的影响,以提升分类的准确率。不同的特征提取方法有不同的效果,LBP的特性是较能排除光照变化且运算速度快。LBP的核心观念是计算每个像素和周围像素间”相对”的关系。通常光照对图中的物件带来的影响是全局的,也就是说照片中的物体的明暗程度,都往同一个方向改变,可能是变亮或变暗,只是改变的幅度会因为距离光源的远近而有所不同。所以基本上局部相邻(Local)的像素间,受光照影响后数值也许会改变,但是相对大小不会改变。
1.原始LBP
LBP特征是根据相邻的像素点与中间相邻点相比的大小确定值为1或0,即如果相邻像素的值大于或等于中间像素的值,则值为1;如果小于则值为1.然后对每个像素点的领域信息进行整合,变为领域个位的数的编码。然后对一个块中所有像素的编码进行直方图的统计,得到LBP特征
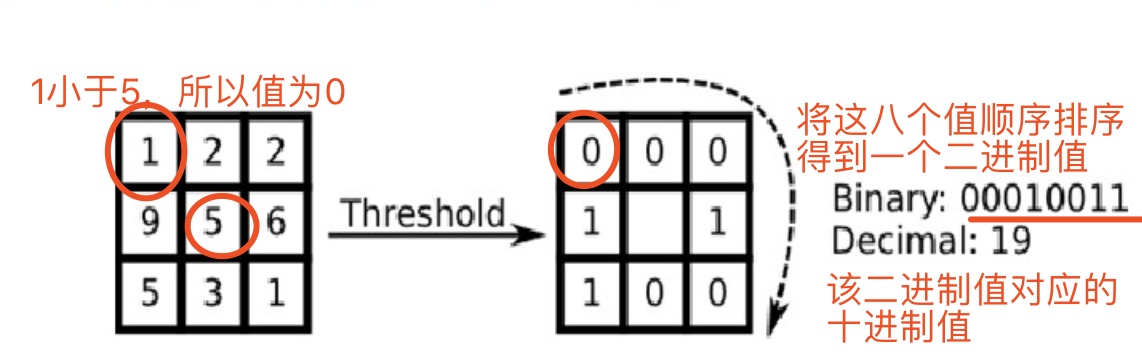
注意:对于邻域像素顺序的规定并没有明确,默认为水平方向左侧为起始点,逆时针旋转
其公式定义为:

s(x)函数就是计算相邻位置像素与中间位置像素的差值,大于或等于中间值,即x为正数或0时返回1;否则为0。
p即该中间像素依据的邻近像素的个数,如上面的例子p为8,左上角的值对应的十进制值的计算为0*2(p-1) = 0*2(8-1) = 0,其下面位置的值为1*20 = 1,最后各个位置计算得到值LBP(xc,yc) = 19,即这个中心点(xc,yc)的LBP值
总结:这个方法可以很好地捕捉到图像中的细节,但是固定的近邻区域对于尺寸变化的编码失效。为了适应不同尺度的纹理特征,将3*3的固定领域扩展到了任意领域,并用圆形代替正方形
2.圆形LBP
改进后的LBP算子允许在半径为R的圆形领域有多个像素点
LBPpR表示在半径为R的圆内有p个像素点
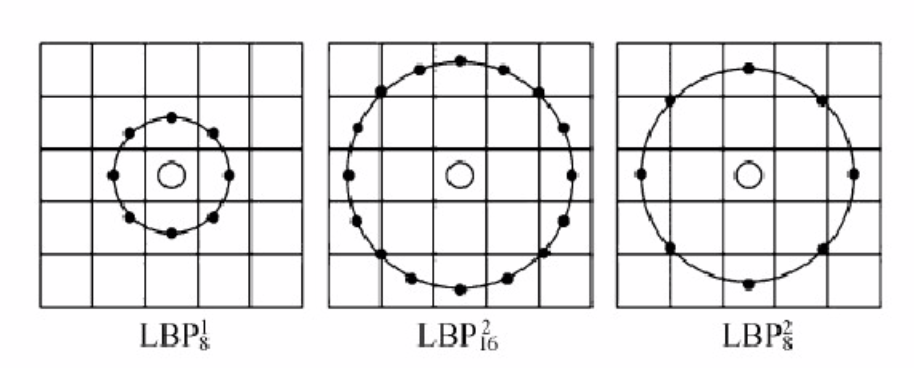
在上面的图像中,第一幅图像的圆半径为1,采样的点为8个;第二幅图像的圆半径为2,采样的点为16个;第三副图像的圆半径为2,采样的点为8个
一般来说,当领域采样点个数相同时,半径越小,图像纹理越精细;当半径相同时,领域采样点个数越少,图像亮度越低,区分度变差。如半径都是3的区域,分别划分为4个和8个采样点,4个采样点只有24种灰度值,区分度肯定没有28种灰度值的好
这样子采样点的坐标计算如下:

当近邻点不在图像的坐标上时,其对应的像素值使用双线性插值算法计算,可见最邻近插值算法和双线性插值算法——图像缩放
3.旋转不变性
此时的LBP特征是灰度不变的,但是不是旋转不变的。同一幅图像,进行旋转后,其特征将会有很大的差别,因为像素位置发生了变化。
实现旋转不变形的方法:不断旋转圆形领域得到所有可能的初始定义的LBP值,然后取其中的最小值作为该领域的值
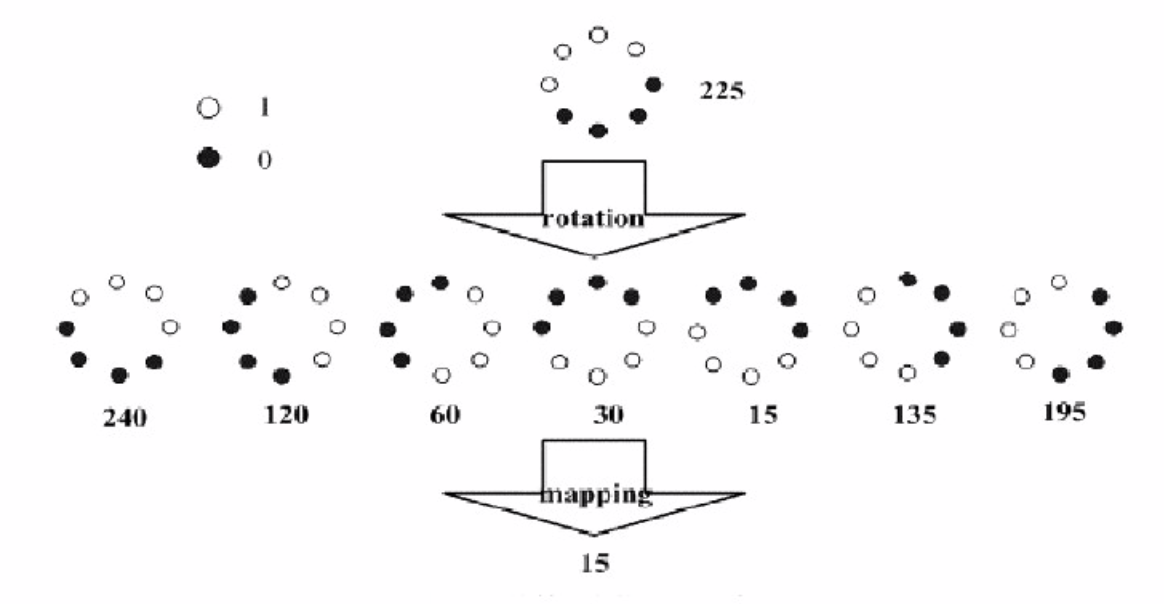
即上图的例子中对应的LBP特征都是00001111,对应的十进制为15
4.等价模式(uniform pattern)
一个LBP算子可以产生不同的二进制模式,对于LBPpR将会产生2p种模式。比如3*3领域内有8个点,则有28种模式;7*7领域内则有236种模式
如此多的二值模式对于信息的提取、识别都是不利的。如果使用这样的LBP模式的统计直方图表示图像的信息,过多的模式种类将使得数据量多大,且直方图过于稀疏
解决办法: 对LBP算子的模式种类进行降维
Ojala认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变

因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)
另一种说法是说其实00000111也算是两次跳变,因为这是个圆形模式,理解即可
通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的2P种减少为 P*( P-1)+2种,其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。

当然,最后还要加上一种混合模式,所以最后的公式为P*( P-1)+2+1 = P*( P-1)+3,所以对于3×3邻域内8个采样点来说,最终的模式数量为59种
通过LBP特征的定义,可见LBP特征对光照变化是鲁棒的,效果如图:

5.LBPH
LBPH,Local Binary Patterns Histograms,即LBP特征的统计直方图,LBPH将LBP特征与图像的空间信息结合在一起。
计算该统计直方图的步骤如下:
- 计算图像的LBP特征图像,即上面的所说的计算方式,为每个坐标计算其的LBP(xc,yc)值
- 然后将整个LBP特征图像进行分块,Opencv中默认将LBP特征图像分成8行8列64块区域
- 然后分别计算每块区域的特征图像的直方图,即统计该区域中所有像素点的LBP(xc,yc)值(该值有[0,2p-1]的2p种情况,p为采样点个数)的分布情况,假设该区域中有3个点的LBP(xc,yc)值为20,则统计该LBP(xc,yc)值=20对应的分布值为3。这样最后一个区域就能够得到一个(1*2p)大小的特征向量,即直方图分布情况。最后将所有区域的直方图结果,即特征向量进行归一化
- 最后将所有区域的特征向量按分块的空间顺序一次排列成一行,形成LBP特征向量,大小为1*(2p*64),这个特征向量就能够用来表示一张图像了
当采样点数p为8时,如果使用的是原始模式的LBP,对应的LBP(xc,yc)值个数为28 = 256,则最后得到的LBP特征向量的维度为256*64 = 16384维;如果使用的是等价模式,则最后的特征向量的维度为59*64=3776维。可以看出,使用等价模式特征,其特征向量的维度大大减少,这意味着使用机器学习方法进行学习的时间将大大减少,而性能上没有受到很大影响
最后可以使用卡方来计算两个图像对应的两个直方图的差异:




