人脸识别和检测中loss学习 - 9 - ADDITIVE MARGIN SOFTMAX FOR FACE VERIFICATION- 1 - 论文学习

 

该方法通过减法的方式将边际margin参数m引入softmax中，cosθ - m

原始的softmax loss函数为：

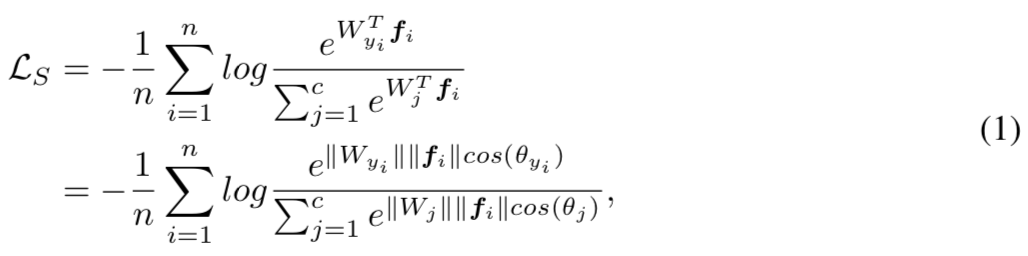
f表示的是最后一个全连接层的输出(fi表示的是第i个样本)，Wj表示的是最后全连接层的第j列。W_yi^Tf_i被叫做target logit

在A-softmax损失函数中，则是会对权重向量进行归一化，即||W_i|| = 1,并将target logit从 ||f_i||cos(θ_yi) 改成 ||f_i||ψ(θ_yi)：

m通常是一个比1大的数，λ则是一个用来控制分类边界多难推进的超参数，从1000退到一个小的值使得每个类的角度空间变得越来越紧凑（即类内距离）（annealing策略，退火策略）

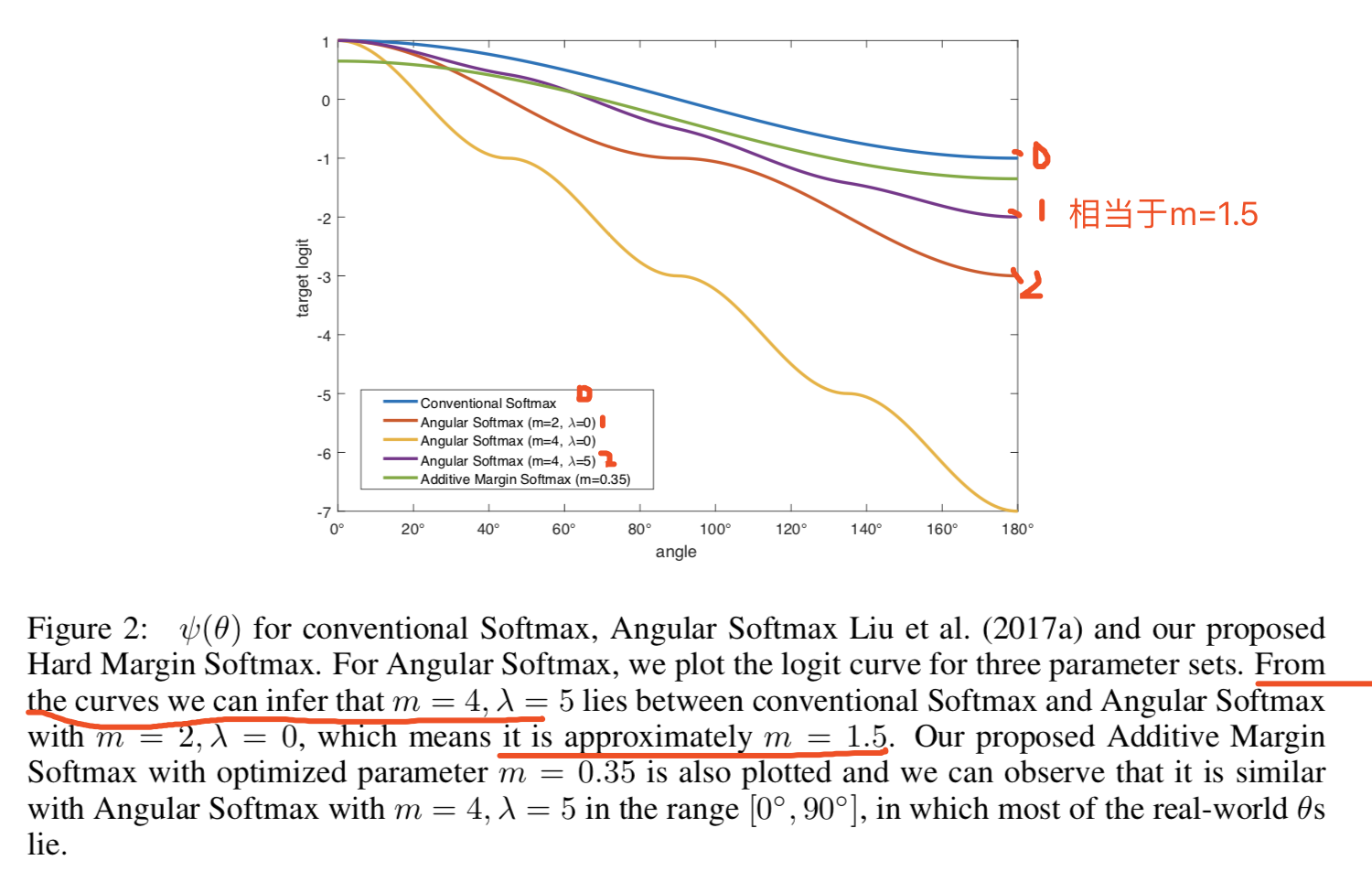
实验中一般设置λ的最小值为5，且m=4；等价于λ=0，m=1.5，如图2所示：

 

 

ADDITIVE MARGIN SOFTMAX

在我们的方法中定义：

其与A-Softmax中定的m的效果类似，可以达到减小对应标签项的概率，增大损失的效果，因此对同一类的聚合更有帮助

对权重和特征都进行归一化，添加一个归一化层在全连接层后面：

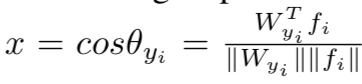
 所以前向传播只用计算：

 然后根据NormFace中的概念使用一个超参数s来scale这个cosine值，最后损失函数为：

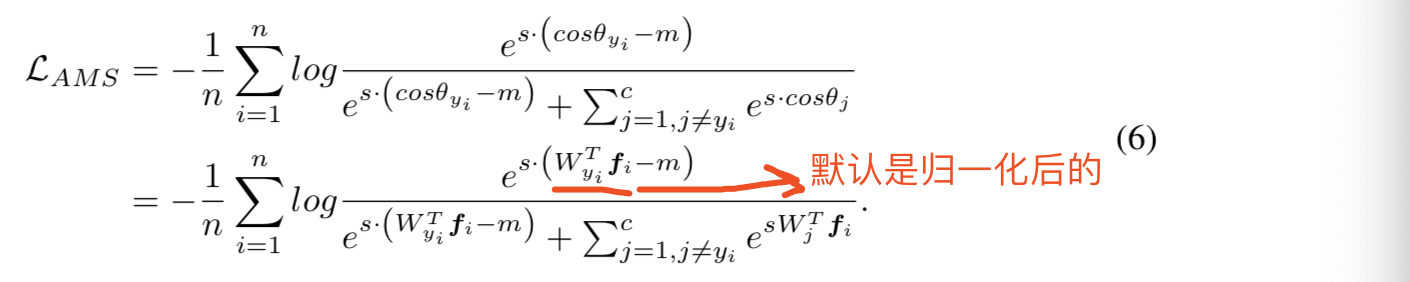
当我们将margin（即m参数）引入损失函数后，我们发现如果让s参数是可学习的，s将不会增加，且网络拟合得很慢。因此打算将s固定在一个足够大的值，即30，用来加速和固定优化器

 

λ的微调是比较困难的，在该margin策略中，我们发现我们不再需要该退火策略。而且即使我们固定了超参数m，网络也能够很灵活地拟合

 

 

3.2.1 GEOMETRIC INTERPRETATION

如图3所示：

 特征是2维的。传统的softmax loss的决策边界为P₀，有，角度边际和余弦边际是等价的

 

 对于我们的AM-softmax，边界变为边际区域而不是单一向量。对于类1的新边界P1，我们有，其中

 如果我们进一步假设所有的类有着相同的类间方差且P₂是类2的边界，可以得到

因此，也就是第一类的余弦值在边缘区域两边的差值。

 

 

3.2.2 ANGULAR MARGIN OR COSINE MARGIN

 在SphereFace中，边际m是与θ相乘的，即cos(mθ), 所以角度边际是通过乘法的方式与损失合并的。我们提出的损失的边际是通过附加的方式与损失合并的,即cosθ - m 。这是两者最大的区别

还值得一提的是，除了强制边际的方法不同，这两种边际公式的基值也不同。一个是θ，另一个是cosθ。虽然cosine边际（cosθ）通常有着到角度边际（θ）的一对一映射，但是因为cosine函数的非线形诱导，在优化他们的时候还是有一些不同的

我们是否使用cosine边际主要取决于最后的损失函数优化使用的相似度度量方法（或距离）

很明显，我们更改后的softmax loss优化的是cosine相似度，而不是角度。如果你使用的是传统的softmax loss方法，这可能不是一个问题，因为这两种形式的决策边界是相同的 （cosθ₁ = cosθ₂ => θ₁ = θ₂）。但是当我们想要推进这个边界的时候，我们将会面临一个问题，即这两个相似度（距离）有着不同的密度。cosine值在角度在接近0或π的时候更密集。

之所以选择cosθ-m而不是cos（θ-m），是因为如果我们想要优化一个角度，在W^Tf这个内积值获得之后将需要一个arccos操作。它的计算开销可能会更大

一般来说，角边际（SphereFace）在概念上比余弦边际（本论文方法）好，但考虑到比较成本，余弦边际更有吸引力，因为它可以用更少的努力实现相同的目标。

 

 

 

3.2.3 FEATURE NORMALIZATION

 

相比SphereFace，本方法添加了特征归一化，为什么？

原因于图像质量相关，从论文（L2-constrained Softmax Loss for Discriminative Face Verification）中图1可见：

 

 

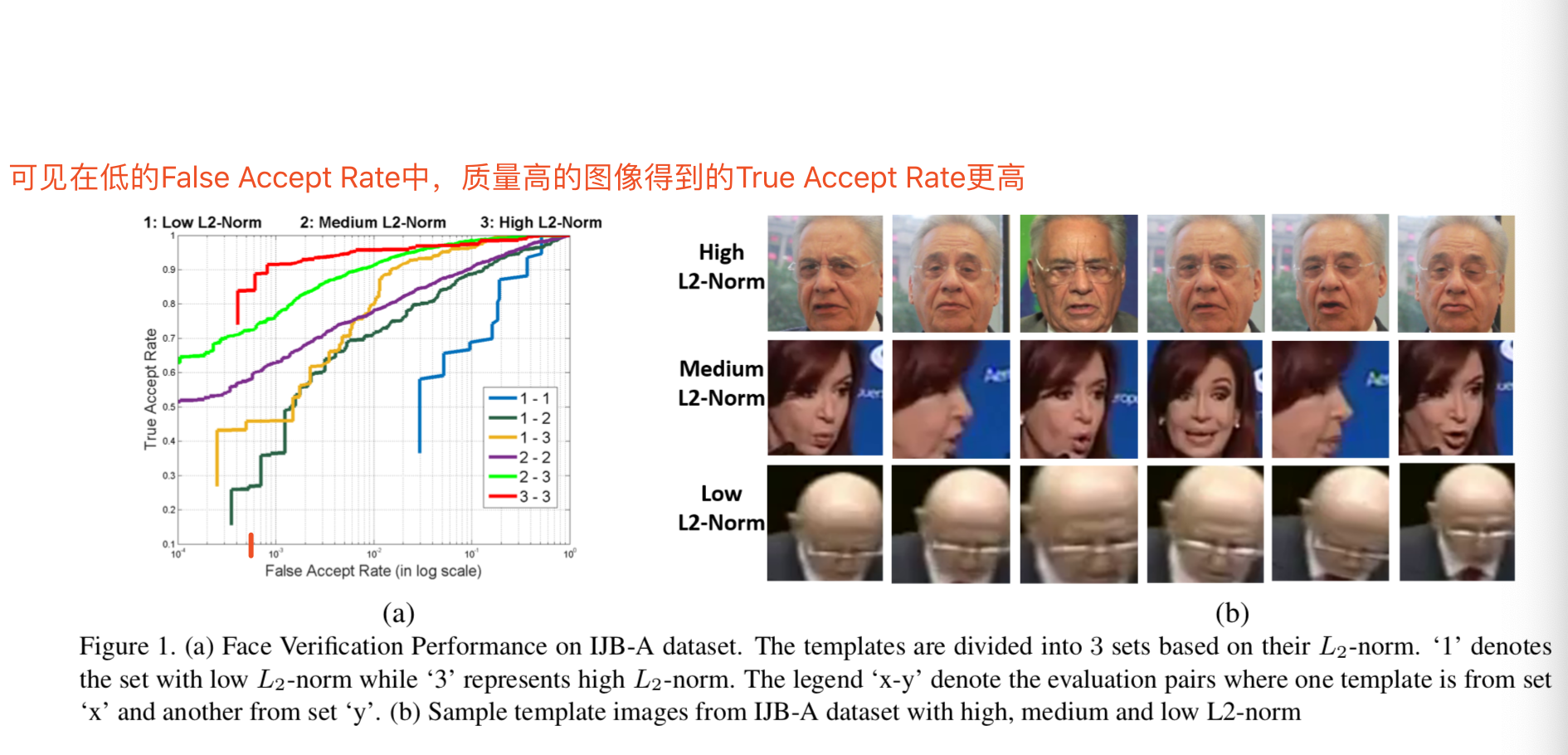
 特征范数||x||₂与图像的质量密切相关。注意后向传播有如下的属性：

 

 

可见在经过归一化之后，对比于有着大的范数的特征，有着小的范数的特征将会得到更大的梯度

 

 

 

 这样经过归一化后，后向传播时网络将会更关注低质量的图片（即有着低范数的图片），这样的效果和我们做困难样本挖掘的效果是相同的，能够使网络训练得更好

因此可知特征归一化比较适合图像质量比较差的任务

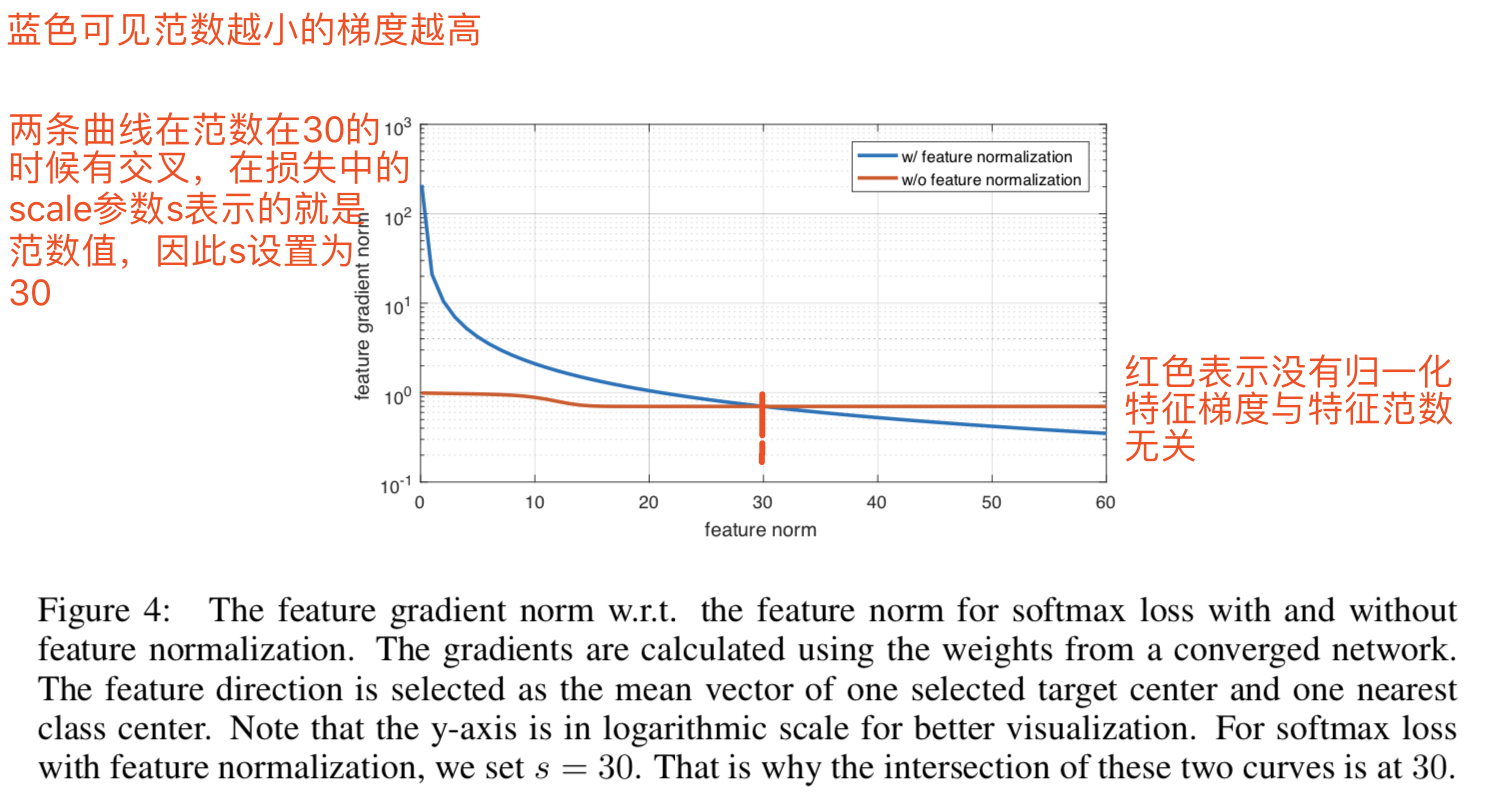
从图4可知当特征范数特别小的时候，梯度可能特别大。这可能会潜在增加梯度爆炸的风险，虽然我们可能很难遇见很多有着很小范数的样本

也许某些特征-梯度范数曲线位于图4中两条曲线之间的权重调整策略可能会有更好的效果。这是一个值得今后研究的有趣课题。

 

 

3.2.4 FEATURE DISTRIBUTION VISUALIZATION

在同样的结构上使用不同的损失函数，输出3维的特征。对于获得的3维特征，归一化并将他们绘制在三维空间的超球体上，如图5:

 

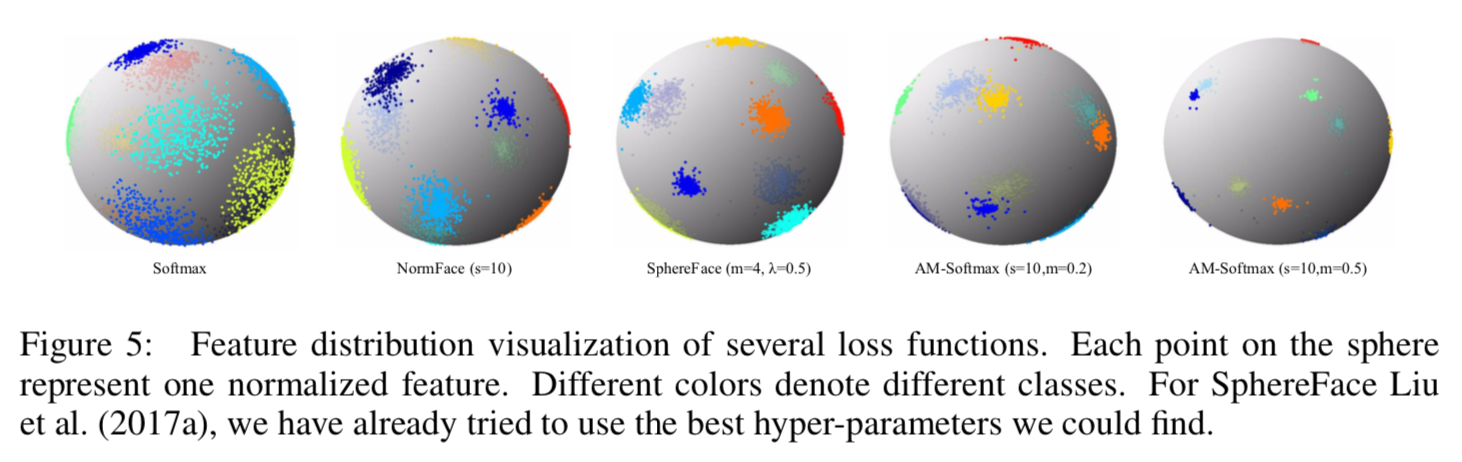
 可见我们参数设置为s=10、m=0.2的AM-softmax的效果和SphereFace的效果相似。我们的损失能够通过设置更大的m来进一步缩小类间方差。与A-softmax相比，有着恰当的scaling因子s的AM-softmax也更易于收敛。该可视化特征很好地说明了AM-softmax能够给特征带来更大的边际属性，而不需要过多的超参数

 

4.3 EFFECT OF HYPER-PARAMETER m

在我们的损失函数中有两个超参数，一个是scale参数s，另一个是margin参数m。scale参数s在之前的工作中都经过了足够的讨论，认为设置为一个足够大的值即可，20到30之间。因此我们的损失函数的主要超参数是margin参数m。当m=0.25到3时，性能显著增强，当m=0.35到4时效果最好

• 不使用特征归一化，在高质量图片集（LFW）上结果更好
• 使用特征归一化，在具有很多低质量的图片集（MegaFace）上结果更好。

图6绘制了两个曲线，可见当rank和false positive rate很低的时候，我们的损失函数的性能都比其他的损失函数好：