NormFace: L2 Hypersphere Embedding for Face Verification - 1 - 论文学习
To sum up, the Cosine Loss[17], vMFMM[21] and our proposed loss functions optimize both features and weights, while the L2-softmax[24] normalizes the features only and the SphereFace[35] normalizes the weights only.
We reduced the number of the feature dimension to 2 and plot 10,000 2-dimensional features from the training set on a plane in Figure 2. From the figure, we find that f2 can be much closer to f1 than to f3 if we use Euclidean distance as the metric. Hence directly using the features for comparison may lead to bad performance.
同时发现对比欧式距离或内积操作,特征向量的角度可能是一个好的度量。当然,以前很多工作都使用过该方法
对于softmax loss来说最常用的相似度度量还是没有归一化特征的内积,该度量使用在训练和测试时有gap
假说1:

公式2的意思是i取[1,n]个类别进行计算,得到最后最大值的索引为i,则说明这个特征向量f对应的图像的类别为i,所以下面的不等式才会成立:
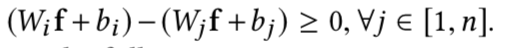
当i == j时该不等式等号成立
假说证明:

这个命题意味着,softmax损失总是鼓励分离良好的特性具有更大的量级。这是为什么softmax的特征分布总是呈发射状的原因
但是如图2所示,我们可能并不需要这个特性:
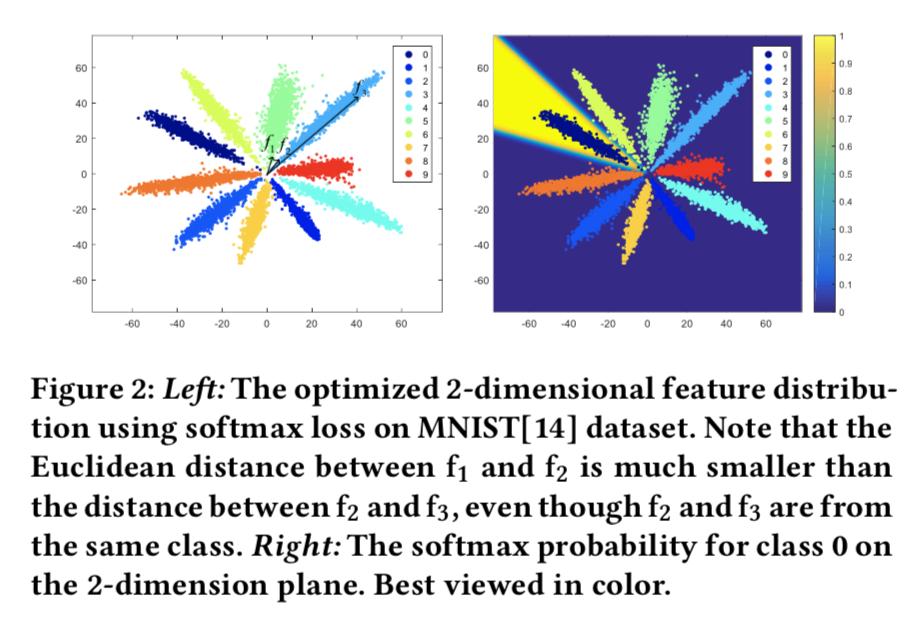
同类f2和f3的距离大于不同类f1和f2的距离
通过归一化可以减轻这个特性的影响。因此我们通常会使用两个特征向量之间的cosine值用来测量两个样本的相似度
但是假说1在内积操作后添加偏置bias的情况下不成立。实际上,两个类的权重向量可以相同,这样模型将仍能够通过bias来做决策。我们在MNIST实验中发现了这样的例子,他们的分散点如图3所示:
我们可以从上面的两张图发现一些类的点都集中在0点周围。这时候进行归一化,来自这些类的点将会分散在一个单位圆中,与其他类香覆盖。可见特征归一化江破坏特定类的区分能力。因此在分类任务中,我们通常在softmax loss前将bias项去掉
首先定义二范数为:

然后归一化层为:
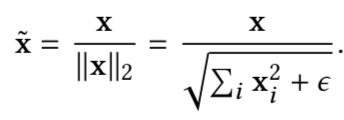
这里的x可以是特征向量f,也可以是权重矩阵Wi中的一列
然后损失函数对归一化层的求导如下:

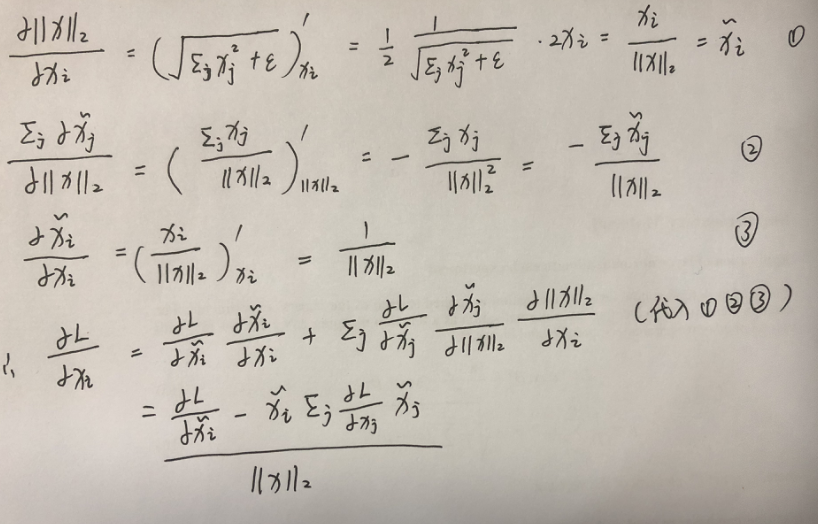
论文中的证明:

Softmax的目标是尽可能最大化正确分类的概率,它会忽略掉一些比较难分辨的图片,也就是低质量的图片,而优先拟合高质量的图片。但是我们有时更希望训练的是一个困难样本,这样训练出来的网络才会更好
一般高质量图像提取出来的特征范数||x||2大,低质量图像提取出来的特征范数||x||2小,因此根据上面的式子可知范数较小的特征会获得更大的梯度,这样网络可能就会花更多的精力去训练质量不好的数据,这样网络的效果会更好,所以进行特征归一化
因此把特征强行归一化其实就相当于会使得低范数的图片变得高范数的图片,增加更多的网络注意力
- 不使用特征归一化,在高质量图片集(LFW)上结果更好
- 使用特征归一化,在具有很多低质量的图片集(MegaFace)上结果更好。
向量x和损失对x求导的值是正交的,所以:
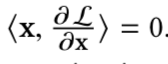
论文中的证明:

从图4的左图可知||x||2总是在增加:

所以为了阻止x的范数||x||2增加到无穷,向量x需要权重衰减项
有了上面的归一化层,我们就能够优化我们的cosine相似度量了:
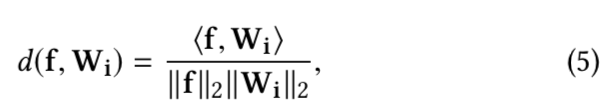
f表示的是特征向量,Wi表示的是在softmax loss层前的内积层权重矩阵的第i 列
但是在归一化之后,网络没能成功收敛。在很多次迭代后损失只降了一点,且收敛到了一个很大的值。之后损失就不降了
这可能是因为归一化后d(f,Wi)的范围为[-1,1],然后没使用归一化前,即使用内积层和softmax loss的值在(-20,20)和(-80,80)
因为该值范围过小的原因,可能回导致概率![]() 不能很好地接近1,即使是在样本分离良好的情况下。yi是f的真正标签值
不能很好地接近1,即使是在样本分离良好的情况下。yi是f的真正标签值
f和其标签对应类的权值向量Wf的内积为1,而与其他类的权值向量内积都是-1,表示差别很大,然后带入上面的概率公式得到:
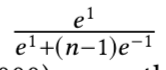
在极端情况下,这个值是很小的。当n=10时其值为0.45;但当n=1000时值为0.007,即当需要分类的数量越大,其离概率1这个值越远,即使数据是很好分类的。即使是在其他类的样本都在单位超球面的另一侧(表示其他类和这个类的差别是很大的),这种情况下得到的概率值离1也很遥远
因为softmax loss函数求导结果公式为 1-Pyi,因为此时的Pyi总是远远小于1,所以即使是在有着分类良好的样本的情况下,求得的偏导结果(梯度)总是很大,使得网络不能收敛
为了更好地理解这个问题,我们将给出一个边界证明在最好的情况下softmax loss有多小
假说2(Softmax Loss Bound After Normalization):
假设每个类都有着相同的样本数;且每个样本都是好分离的,即每个样本的特征和他们对应类的权重是相同的,所以Wi == f。这样如果我们归一化特征和权重的每一列,将得到一个项(下式的花体L),这样softmax loss将有一个下界:
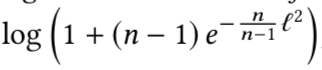
n表示类别的数量
证明:


这个界限意味着,如果我们只是将特征和权重标准化到1,即使不应用正则化,softmax的损失也会被限制在训练集上的一个非常高的值
为了对这个界有一个直观的认识,我们还在图5画出了作为范数花体L的函数的这个界的曲线:

获得了这个边界后,收敛的问题就很清楚了
解决办法就是将特征和权重列归一化到一个更大的值范数花体L而不是1,这样softmax loss就能够继续往下降了。我们通过直接添加一个scale 层在cosine层后面来学习。该scale层就只有一个可学习参数:
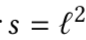
根据图5我们可能回固定它到一个足够大的值,对于不同的类数量,设置为20到30之间的值
但是我们更希望它是一个能够通过后向传播自动学习的值
因此最后带有cosine距离的softmax loss将被定义为:
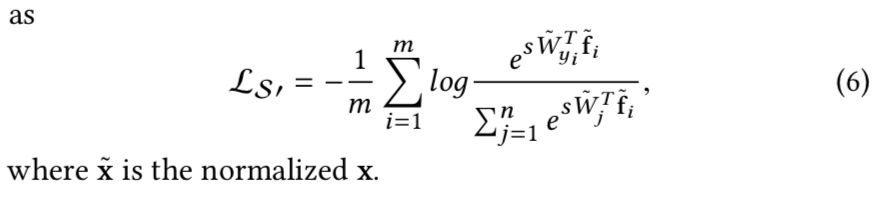
Metric Learning度量学习
深度度量学习通常喜欢使用成对或三个样本作为输入,然后输出他们之间的距离。在度量学习中归一化是一个常用策略,对于其损失函数没有导致什么问题。
但是度量学习比分类难训练,因为它的输入对很大,对于成对数据来说可能是O(N2),对于三对数据来说可能是O(N3),N为训练样本数。需要采样和困难样本挖掘算法,时间花费大且棘手。相反分类中的输入数据是O(N)的
因此我们打算重构度量学习损失函数去做分类任务,同时保持他们与归一化特征的兼容性
因为归一化后softmax loss可以被看作归一化的欧式距离:
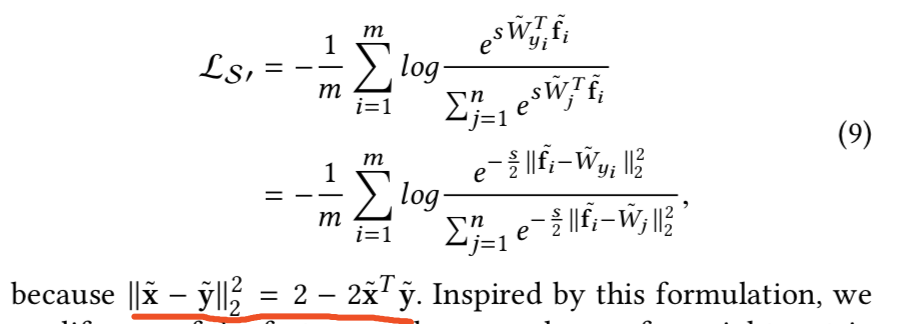
agent策略
即将某类特征与另一类特征之间的距离计算改成某类特征和另一类特征的总结Wj的距离计算,这样在训练的时候就不用进行成对数据或成三对数据的配对了
1)contrastive loss:
从:
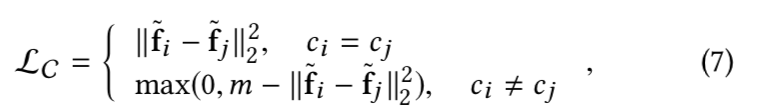
变成C-contrastive:

这里的m参数就是设置的margin值,表示当该特征和该W~j不是一类时,他们之间的距离最好是大于m这个边际值的,这样它在损失中就不会起作用,因为为0,不会被优化;如果小于他就会对损失其作用
2)triplet loss:
从:

变成C-triplet:
![]()
这里的m值也是表示边际值margin,即表示当i、j为一类,i、k不为一类时,不为一类的距离应该比为一类的距离大m,这样就不会被优化,表示此时类之间分离良好
这些改后的损失函数是用来做分类的
为什么能够Wj能够替代特征fj:
Wj表示的是第j类特征的总结,其在论文中称为agent。如果所有类都能通过边界很好地分离,则Wj就能很好地对应每个类的特征均值,如图6左图所示:

右边的图是比较复杂的情况,就是所有类并不能很好分离,有些样本相互重叠,这样agent将会有所偏移。这样边际特征(即困难样本)将会有更大的梯度,这就使得在更新时他们移动得比容易的样本大
但是这个agent策略也会有缺点。即在重构后,如果我们仍然使用与原始版本相同的边际margin(即式子中的m参数值),一些边际margin特征可能不会得到优化。如图7:
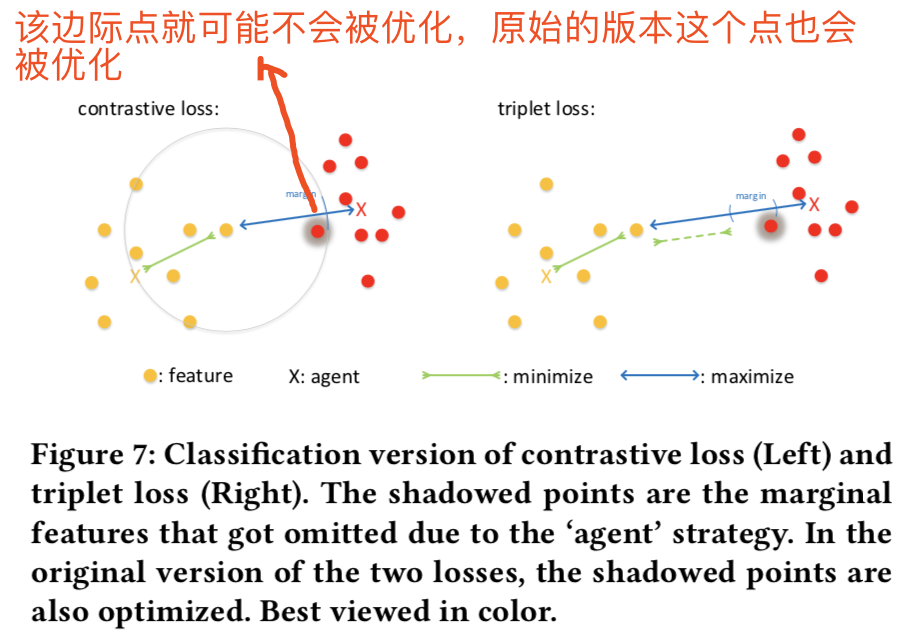
如上图所示的例子,假设黄色的agent为W0,红色的agent为W1。
- 左图:即对于中间的黄点fi,它与非同类W1的距离|| fi - W1 ||2 2(蓝线线)是小于设置的边际值m(margin,即圆圈的直径)的,这样他就会被优化,会训练得越来越接近W0 ; 而灰色的红点fj与非同类的距离|| fj - W0 ||2 2是大于设置的边际值m(margin)的,这样它就不会被优化了。 而原始的版本是和非同类的任意选择的特征点fk对比,所以距离大概率是小于边际值的,所以会被优化
- 右图:即对于中间的黄点fi,它与非同类W1的距离|| fi - W1 ||2 2(蓝线线) 减去 同类W0的距离|| fi - W0 ||2 2(绿线) 的结果是小于设置的边际值m(margin)的,所以会被优化;而灰色的红点是大于边际值的,所以不会被优化
所以我们需要更大的边际margin值使得更多的特征被优化。
数学上,该由agent近似引起的误差由以下命题给出:
假说3:

f0是A类的特征,fj是B类的特征,Wi是B类的特征总结agent。即两类特征的距离 减去 一类特征与另一类特征总结agent的距离的平方结果是有一个上界的,上界为一类的特征与该类特征总结agent的距离
即三角不等式:

论文中证明:

这个边界bound为我们设置边际margin提供了理论指导。我们可以在训练过程中使用移动平均法实时计算它,并将其显示出来,以获得更好的进度感觉。
理论上,该边界bound![]() 通常为0.5到0.6
通常为0.5到0.6
则对于contrastive loss和triplet loss推荐的边际值margin分别为1和0.8
注意,设置边际margin曾经是一项复杂的工作。遵循这些方法,我们不得不暂停训练,每隔几个epoch就寻找一个新margin。但是,在应用了归一化之后,我们不再需要执行这样的搜索算法。通过归一化,特征量的大小scale(即参数s)是固定的,这使得确定margin(即参数m)也成为可能。在这种策略中,我们将不会尝试使用不进行归一化的C-triplet损失或C-contrastive损失来训练模型,因为这很困难。



