Dense 3D Face Decoding over 2500FPS: Joint Texture & Shape Convolutional Mesh Decoders - 1 - 论文学习
Abstract
3D Morphable Models (3DMMs)是一种统计模型，它使用一组线性基和更特殊的主成分分析(PCA)来表示面部纹理和形状的变化。采用3DMMs作为统计先验，通过求解非线性最小二乘优化问题，从图像中重建三维人脸。最近，3DMMs被用作训练非线性映射的生成模型。通过深度卷积神经网络(Deep Convolutional Neural Networks, DCNNs)将图像转换为模型的参数。然而，以上所有的方法要么使用全连接层，要么在参数化的展开UV空间上使用二维卷积，从而得到具有许多参数的大型网络。在本文中，我们提出了第一个非线性3DMMs，通过使用直接网格(direct mesh)卷积学习联合纹理和形状自动编码器。我们演示了如何使用这些自动编码器来训练非常轻的模型，在自然环境下以超过2500帧/秒的速度执行彩色网格解码(Coloured Mesh Decoding，CMD)。
1. Introduction
二十年前，Blanz和Vetter展示了一个非凡的成就[2]。他们证明了从一张图像中重建三维面部几何结构是可能的。这是有可能的，通过解决一个非线性优化问题，其解决空间被一个三维面部形状和纹理的线性统计模型，即所谓的3D Morphable model (3DMM)所限制。基于3DMMs的方法仍然是最先进的三维面部重建技术，即使是从自然环境下捕获的图像[6,4,5]重建。
在过去的两年中，人们就如何利用深度卷积神经网络(DCNNs)从二维人脸图像中获取三维形状和纹理信息进行了大量的工作。第一种方法是训练DCNNs从图像到3DMM[36]的参数的回归，或者使用3DMM合成图像，利用DCNNs[31]形成一个图像到图像的转换问题来估计深度。最新的、更复杂的、基于DCNN的方法使用自监督技术进行训练[17、37、38]，并利用可微的图像形成体系结构和可微渲染器[17]。最近的方法，如[37,38]和[34]使用自监督方法在纹理和形状方面超越了标准的3DMMs方法。特别是，[34]同时使用了3DMMs模型和其他网络结构(称为correctives)，它们可以捕获3DMMs空间之外的信息，以表示形状和纹理。[37,38]中的方法尝试学习直接来自数据的形状和纹理的非线性空间(即，解码器，即所谓的非线性3DMMs)。然而，为了避免训练效果不佳，这些方法在模型预训练前使用了3DMMs配件。
在上述所有方法中，线性或非线性解码器形式的3DMMs，要么使用全连接的节点[36]进行建模，要么(尤其是在纹理空间中)使用未封装的UV空间上的2D卷积进行建模[37,38]。在本文中，我们采取了一个完全不同的方向。出于对几何深度学习(GDL)领域的研究,试图概括DCNNs到非欧几里得域，如图表/manifolds/网格(33,12,21,7,27],我们第一次尝试开发一个使用mesh卷积的非线性3DMMs来描述形状和纹理。除了使用网格卷积更直观地定义非线性3DMMs外，它们的主要优点是由参数数量非常少的网络定义，因此计算复杂度非常小。
综上所述，本文的贡献如下:
- 我们展示了最近用于发现稠密或稀疏对应的技术(例如，densereg[18]，路标定位方法[40])如何可以很容易地扩展到利用网格卷积解码器来估计三维面部几何信息。
- 我们展示了据我们所知第一个使用网格卷积的非线性3DMM。该方法直接在网格域上对形状和纹理进行解码，具有紧凑的模型大小(17MB)和惊人的效率(在CPU上超过2500 FPS)。该解码器不同于最近提出的[27]解码器，该解码器仅对三维形状信息进行解码。
- 我们提出了一种编码器-解码器结构，可以直接从自然环境中的二维面部图像重建纹理和形状。由于提出的彩色网格解码器(CMD)的效率，我们的方法可以估计超过300帧/秒的三维形状(对于整个系统)。
2. Related Work
在接下来的文章中，我们将简要讨论相关的文献主题，如线性和非线性的3DMM表示。
Linear 3D Morphable Models. 在过去的二十年中，用于表示和生成3D人脸的方法主要是主成分分析(PCA)。在许多著作[2,3,29]中都使用PCA建立统计三维形状模型(即， 3D Morphable Models (3DMMs))。最近，主成分分析法被用于构建三维人脸[6]和头[11]的大规模统计模型。将面部特征的变化与表情的变化相分离是表征和生成人脸的重要方法。因此，我们引入了统计混合形状模型，该模型仅表示使用PCA的表情变量[22,9]。原始的3DMM[2]使用PCA模型来描述纹理变化。然而，这对从自然条件下捕获的图像来说是相当有限的描述纹理变化的方法。
Non-linear 3D Morphable Models. 在过去的一年中，人们首次尝试学习非线性的3DMMs[37,38,34]。这些3DMMs可以看作是使用DCNNs的解码器，再加上一个图像编码器。具体来说，[34]方法采用了自监督的方法来学习一个新的具有全连接层的解码器，该解码器将线性3DMM与能够重构任意图像的新结构相结合。类似地，这些方法[37,38]使用全连接层或UV图上的2D卷积来解码形状和纹理。
以上方法均采用全连接层或二维卷积来定义非线性3DMM解码器。然而，这些方法导致了具有大量参数的深度网络，并且没有利用三维面部结构的局部几何特征。因此，能在非欧几里得人脸网格域中直接使用卷积的解码器需要被构造。非欧几里得域上的深度学习领域，也被称为几何深度学习[7]，最近得到了一些普及。第一个作品包括[23]，它提出了所谓的MeshVAE，它使用来自于[39]的卷积运算符和使用了与光谱Chebyshev过滤器[12]类似的体系结构的CoMA[27]以及额外的空间池来生成3D面部网格这三部分来训练一个变分自动编码器(VAE)，。作者证明了在只有8个维度的非常小的维度潜在空间中，CoMA比PCA更能表示面部表情。
在本文中，我们提出了第一个自动编码器，直接使用网格卷积联合纹理和形状表征。提出了一种高效的彩色网格解码器，可用于来自自然环境下的数据的三维人脸重建。
3. Proposed Approach
3.1. Coloured Mesh Auto-Encoder
Mesh Convolution. 我们定义了基于不定向连通图G = (V, ε)的网格自编码器, V∈Rn×6是一组包含连接点形状(如x, y, z)和纹理(如r、g、b)信息的n个顶点,；ε∈{0,1} n×n是编码顶点之间的连接状态的邻接矩阵。
遵循[12，26],非规范化图拉普拉斯算子(Laplacian)被定义为 L = D − ε∈Rn×n ，其中D∈Rn×n是元素为Dii =∑j εij的对角矩阵； 规范化定义为L = In − D1/2εD1/2,其中 In是单位矩阵。拉普拉斯算子L可以通过傅里叶变换U = [u0，…,un−1]∈Rn×n, L = UΛUT，其中Λ =
diag([λ0,...,λn−1)∈Rn×n。图像傅里叶变换的脸表征x∈Rn×6被定义为xˆ= UTx,和它的逆矩阵为x = Uxˆ。
卷积的操作在一个图表可以定义为通过使用递归切比雪夫多项式[12、26]制定一个带有内核gθ的网格过滤器。过滤器gθ可以被参数化为一个截断K阶切比雪夫多项式展开式：
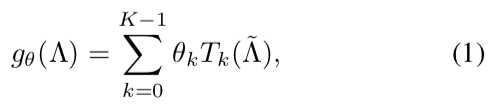
其中θ∈RK是一个切比雪夫系数向量，Tk(Λ̃)∈Rn×n 是k阶切比雪夫多项式在一个按比例缩小的拉普拉斯算子Λ̃= 2Λ/λmax − In上的计算。Tk可以递归计算为Tk(x) = 2xTk−1(x）−Tk−2(x)， T0 = 1, T1 =x。
谱卷积可以定义为：
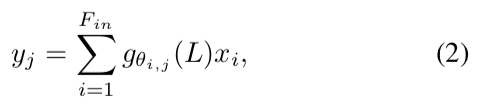
其中x∈Rn×Fin是输入，y∈Rn×Fout是输出。整个过滤操作y = gθ(L) x是非常有效的,只花费了O(K |ε|)大小的操作。
Mesh Down-sampling and Up-sampling. 我们跟随[26]使用二值变换矩阵Qd∈{0,1}n×m对一个顶点为m的网格进行下采样，使用另一个变换矩阵Qu∈Rm×n进行上采样。
Qd是在最小化二次误差[15]的约束下，通过迭代收缩顶点对计算得到的。在下采样时，我们将丢弃的顶点的质心坐标存储在下采样网格中，这样上采样步骤就可以添加具有相同质心位置信息的新顶点。
对于上采样，在向下采样步骤中直接保留的顶点进行卷积变换。在下采样过程中丢弃的顶点将使用记录的重心坐标映射到下采样的网格表面。利用稀疏矩阵乘法对顶点为Vu的上采样网格进行有效预测，即Vu = QuVd。
3.2. Coloured Mesh Decoder in-the-Wild
在自然环境下拟合的非线性3DMM采用无监督/自监督的方式设计。由于我们可以用彩色网格自动编码器来构造连接的形状和纹理基，因此可以把这个问题看作是基和重建3D人脸的最佳系数之间的矩阵乘法。从神经网络的角度来看,这可以被视为一个图像编码器EI(I;θI)被训练回归到3维形状和纹理中,表示为fSA。如图2所示：
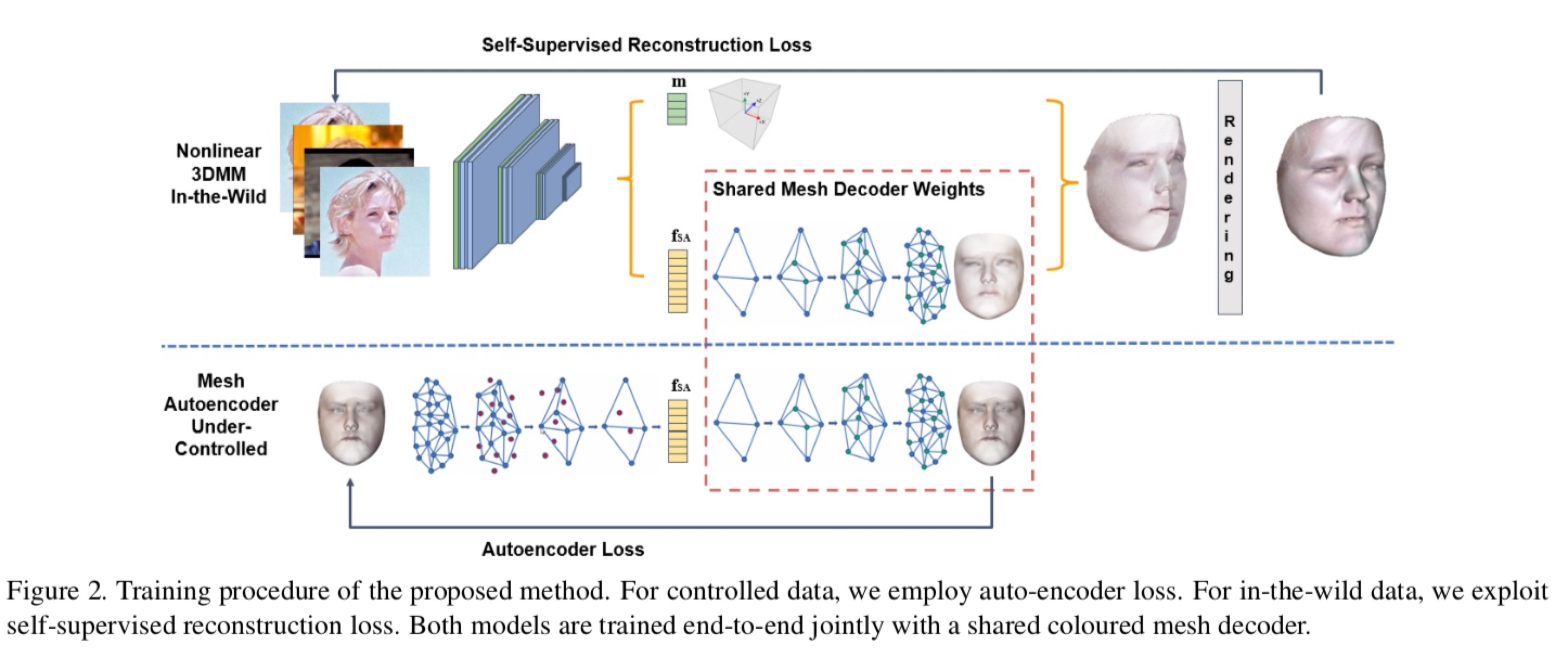
使用二维卷积网络对自然环境下的图像进行编码并接着使用网格解码器D(fSA;θD)解码,解码器D的权重与网格自动编码器中的解码器[10]中共享。然而，联合形状和纹理解码器的输出是一个单位球体内的彩色网格。与线性3DMM[4]一样，相机模型需要将以物体为中心的笛卡尔坐标的三维网格投影到同一个笛卡尔坐标的图像平面中。
Projection Model. 在本研究中，我们使用了一个针孔相机模型，它利用了一个视角转换模型。投影操作的参数可以表示为:
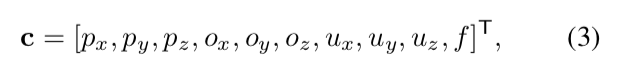
式中，p, o, u分别表示摄像机在直角坐标系中的位置、方向和垂直方向。f是控制透视投影的视场(FOV)。我们还将照明参数与摄像机参数连接起来，作为被图像编码器预测的呈现参数。假设有三个点光源和恒定的环境光，总共有12个参数l用于照明。为了简单,我们表示渲染参数为m = (cT, lT)T是大小为22（c向量10 + I向量12）的向量（图2中encoder的另一个绿色输出）和投影模型函数ˆI = P(D (fSA);m): R3N→R2N。
Differentiable Renderer. 为了使网络是端到端可训练的,我们合并一个可微的渲染器[17]（即上面的函数P）去投射输出网格D (fSA)到图像平面ˆI。L1范数被明智地作为损失函数来计算。渲染器，也称为光栅化器，为图像平面上的每个像素生成质心坐标和相应的三角形IDs。渲染过程包括Phong着色[25]和根据质心坐标插值。此外，相机和照明参数计算在同一框架。整个管道能够进行端到端的训练，通过可微渲染器反向传播损失梯度。
Losses. 我们制定了一个损失函数联合应用于控制下的彩色网格自动编码器和自然环境下的彩色网格解码器，从而实现监督和自监督端到端的训练。其公式如下:
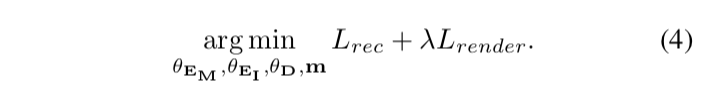
目标函数为：
1）编码-解码器损失：
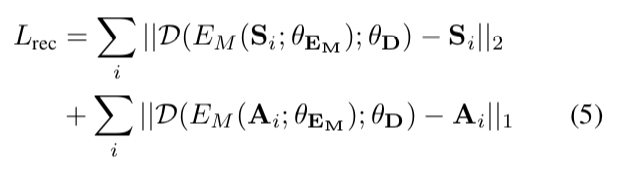
分别对形状S和纹理A应用l2和l1规范，对彩色网格自动编码器进行形状和纹理重构。
2）渲染器的损失：
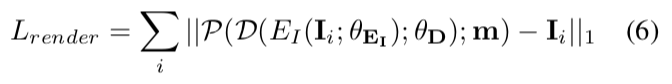
表示当仅对可见的面部像素应用mask时，对自然环境下的图像的像素级重建损失。在训练时我们使用λ= 0.01,然后逐渐增加到1.0。
4. Experimental Results
4.1. Datasets
我们使用控制下的数据(3DMD[13])和自然环境下的数据(300W-LP[40]和CelebA[24])来训练我们的方法。3DMD数据集[13]包含3564个具有不同表情变化的唯一标识的大约21k个原始扫描。300W-LP数据集[40]包含约60k大姿态面部数据，这些数据是通过[40]的profiling方法综合生成的。CelebA数据集[24]是一个大型的人脸属性数据集，拥有超过200k的名人图像，覆盖了大量的姿态变化和背景杂音。每个训练图像被裁剪到有着68个面部定位点的索引的边界框中，带有随机扰动来模拟粗糙的人脸检测器。
我们在AFLW2000-3D [40]， 300VW[30]和CelebA testset[24]上进行了大量的定性实验。我们还与之前在FaceWare-house[8]和Florence[1]上的工作进行了定量比较，在这两个平台上可以获得精确的三维网格进行评估。FaceWare-house是一个由Kinect RGBD摄像头收集的三维面部表情数据库。包含了来自不同种族、年龄在7岁到80岁之间的150名候选人。Florence是一个三维人脸数据集，包含53个目标，他们的真实三维网格从结构光扫描系统获得。
4.2. Implementation Details
Network Architecture. 我们的架构由4个子模块组成，如图2所示，分别命名为Image Encoder[37,38]、Colour Mesh Encoder[26]、一个共享的Colour Mesh Decoder[26]和可微渲染模块[17]。图像编码器部分采用形状为112×112×3的输入图像，然后是10个卷积层。它将输入图像的维数减少到7×7×256，并应用全连接层构造一个256×1维的嵌入空间。每个卷积层后面都有一个批处理规范化层和ReLU激活层。所有卷积层的核大小为3，对任意下采样卷积层的步长为2。彩色网格解码器的嵌入尺寸为256×1，解码为28431×6的彩色网格(3个形状和3个纹理通道)。编码器/解码器由4个几何卷积滤波器[26]组成，每个滤波器后面都有一个向下/向上采样层，该层将顶点数减少/增加4倍。每个图卷积层后面都有一个ReLU激活函数，与图像编码器中的激活函数类似。
Training Details. (1)控制下的彩色网格自动编码器和(2)自然条件下的彩色网格解码器是端到端联合训练的，尽管它们使用不同的数据源。这两个模型都使用Adam优化器进行了训练，初始学习率为1e-4。每个epoch的学习率衰减率为0.98。我们训练了200个epoch的模型。我们用随机翻转、随机旋转、随机缩放和随机剪切的方法使训练图像从136×136的输入变为112×112的大小。
4.3. Ablation Study on Coloured Mesh Auto- Encoder
Reconstruction Capacity. 我们比较线性和非线性3DMMs在表示不同嵌入维度的真实三维扫描的能力，以强调我们的彩色网格解码器的紧凑性。这里，我们使用来自3DMD数据集的10%的3D面部扫描作为测试集。
如图3顶部所示：
我们比较了线性和非线性模型重建结果的视觉质量。为了量化形状建模的结果，我们使用了归一化平均误差(NME)，它是根据眼距归一化的真实形状和重建形状之间的每个顶点的平均误差。对于纹理建模的评估，我们使用了基于真实和重建纹理之间的像素平均绝对误差(MAE)。
如表1所示：
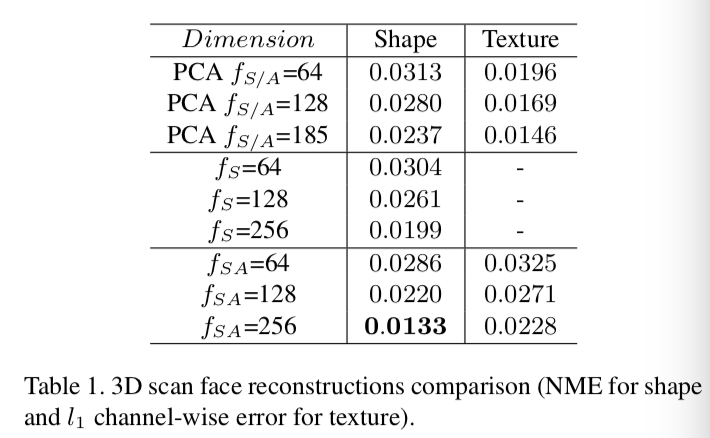
我们的非线性形状模型的形状重构误差明显小于线性模型。此外，该联合非线性模型显著地降低了重建误差，表明整合纹理信息有助于约束顶点的变形。对于纹理重建的比较，由于我们的模型内插了顶点之间缺失的纹理信息，所以纹理的重建误差会略高一些，而线性模型具有完整的纹理信息。
Attribute Embedding. 为了更好地理解彩色网格解码器中嵌入的不同人脸，我们研究了语义属性嵌入。对于一个给定的属性，例如smile，我们将带有该属性
的人脸数据(形状和纹理)输入到我们的彩色网格编码器中，得到嵌入参数
，它代表了该属性在低维嵌入空间中的相应分布。以均值参数fSA为输入训练彩色网格解码器,我们可以重建带有该属性的平均形状和纹理属性。在对嵌入参数进行主成分分析的基础上，可以方便地使用一个变量(主成分)来改变属性。图3显示了一些从潜在空间中采样纹理的三维形状。在这里，我们可以观察到，我们的非线性彩色网格解码器的能力是优秀的建模表情，照明，甚至是带有一个紧密的嵌入尺寸(fSA = 256)的胡子。
4.4. Coloured Mesh Decoder Applied In-the-wild
4.4.1 3D Face Alignment
由于我们的方法可以同时对形状和纹理进行建模，因此我们将其应用于自然环境下的三维形态拟合，并测试了稀疏三维人脸对齐的性能。我们将我们的模型与最新的最先进的方法进行比较，例如在AFLW2000-3D[40]数据集上使用3DDFA[40]、N-3DMM[37]和PRNet[14]。其精度由归一化平均误差(NME)来评估，这是由三个姿态子集[40]的边界框大小归一化的定位点误差的平均值。
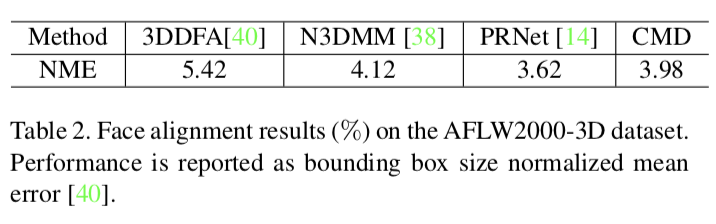
3DDFA[40]是一个级联的CNNs，它迭代地在多个步骤中改进它的估计。N-3DMM[38]利用2D深度卷积神经网络在UV位置和纹理映射上构建非线性3DMM，并以弱监督方式拟合无约束的2D自然环境下的人脸图像。本方法采用彩色网格解码器构建非线性三维模型。我们的模型不仅具有更好的性能，而且具有更紧凑的模型大小和更有效的运行时间。PRNet[38]采用了一个编码-解码神经网络来直接还原UV位置图。由于网络的复杂性，该方法的性能略低于PRNet。
在图4中：
我们给出了一些示例性的对齐结果，这些结果展示了在极端姿态、夸张表情、重遮挡和可变光照下成功的稀疏三维人脸对齐结果。我们还发现稠密形状(顶点)的预测在自然环境下也是非常可靠的，这意味着对于任何类型的面部定位点配置，如果对应我们的形状配置的定位点是给定的，我们的方法都能够给出准确的定位结果。
4.4.2 3D Face Reconstruction
我们首先定性地比较我们的方法与五种最新的最先进的3D面部重建方法:(1)以监督的方式学习3DMM拟合网络(Sela et al .[31]), (2) 一个命名为MoFA的以一种无监督的方式学习的3DMM拟合网络(Tewari et al .[35]),(3)一个命名为VRN的直接体积CNN回归方法(Jackson et al。[19]), (4)一个命名为PRNet的以直接UV位置映射回归的方法(Feng et al .[14]),(5)一个命名为N-3DMM的以弱监督方式学习的非线性3DMM拟合网络(Tran et al。[38])。由于PRNet和N-3DMM都使用了UV位置映射上的2D卷积网络来学习形状模型，因此我们将PRNet和N-3DMM视为与我们的方法最接近的基线。
Comparison to Sela et al. [31]。它们的基本图像到图像的网络是根据线性模型生成的合成数据进行训练的。由于合成图像和真实图像之间的区域间隙，在自然环境中测试时，网络输出在一些被遮挡的区域趋于不稳定(图5)，这将导致后续步骤的失败：
相比之下，我们的彩色网格解码器是在真实世界的无约束数据集上以端到端的自监督的方式进行训练的，因此我们的模型在处理自然环境上的变化方面是健壮的。此外，Sela等人的[31]方法需要一个缓慢的脱机非刚性注册步骤(∼180秒)来从预测深度映射获得无孔重构。然而，提出的彩色网格解码器可以运行非常快。此外，我们的方法是对Sela等人的[31]的精细细节重建模块的补充。使用Shape from Shading(SFS)[20]来完善我们的拟合结果，可以导致更好的结果与细节。
Comparison to MoFA [35]. Tewari等人提出的单眼三维人脸重建方法MoFA采用了一种无监督的方式在自然环境下学习3DMM拟合。然而，它们的重构空间仍然局限于线性基。因此，当处理非常具有挑战性的纹理时，他们的重建将发生非自然的表面变形情况，如图6所示的胡子：
与此相反，我们的方法使用一个非线性的彩色网格解码器来共同重建形状和纹理。因此，我们的方法可以实现高质量的重建结果，甚至是在毛状纹理方面。
Comparison to VRN [19]. 我们还将我们的方法与Jackson等人提出的直接体积回归方法进行了比较。VRN通过带有跳跃连接(即Hourglass结构)的编码-解码器网络直接回归三维形状体，以避免显式使用线性3DMM先验。这种策略可能有助于网络探索比线性模型更大的解决方案空间。然而，这种方法丢弃了人脸网格与回归目标之间的对应关系，使得回归目标的尺寸非常大。图7显示了VRN和我们的方法的三维面部重建的可视化比较：
一般来说，VRN可以很好地处理自然环境下的纹理变化。然而，由于体积形状的表征，表面不光滑，不能保留细节。相比之下，我们的方法直接对顶点的形状和纹理建模，因此模型尺寸更紧凑，输出结果更平滑。
除了与目前最先进的三维人脸重建方法进行定性比较外，我们还对FaceWarehouse数据集[8]和Florence数据集[1]进行了定量比较，以展示我们提出的彩色网格解码器的优越性。
FaceWarehouse. 按照[35,38]中的相同设置，我们还定量地将我们的方法与之前在FaceWarehouse数据集[8]中的9个主题上的工作进行了比较。可视化和定量比较如图8所示：
我们取得了与Garrido等人[16]和N-3DMM[38]相当的结果，同时也超过了其他所有的回归方法[36,28,35]。如图8右侧所示，我们可以很容易地从这三个样本的着色顶点推断出它们的表达式。
Florence. 根据[19,14]中的相同设置，我们还对我们的方法与Florence数据集[1]上的最新方法(例如VRN[19]和PRNet[14])进行了定量比较。从真实点云计算人脸边界框，裁剪人脸图像作为网络输入。在如[19,14]对每个主题配置的不同的姿态:倾斜旋转-15◦、20◦和25◦和在-80◦和80◦之间进行原始旋转。我们只选择了公共面区域来比较性能。为了进行评估，我们首先使用Iterative Closest Points(ICP)算法来找出模型输出与真实点云之间对应的最近邻点，然后计算由三维坐标眼间距归一化的均方误差(MSE)。
从图9(a)可以看出，我们的方法得到了能与PRNet比较的结果：
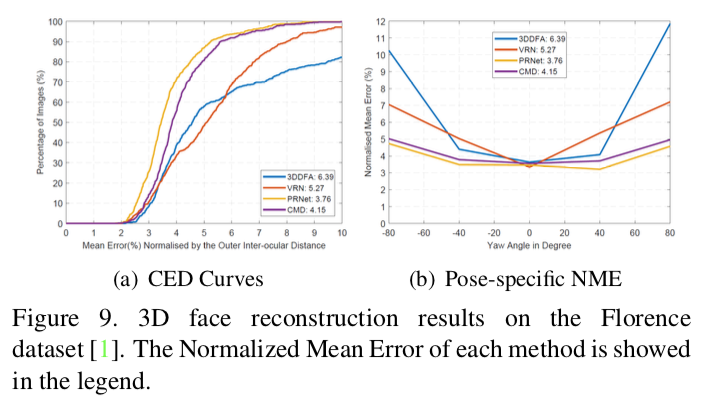
为了更好地评估我们的方法在不同姿态下的重建性能，我们计算了不同偏航角下的NME。如图9(b)所示，所有的方法在近正面视图下都获得了良好的性能。然而，随着偏航角的增加，3DDFA和VRN不能保持较低的误差。我们的方法在姿势变化下的性能相对稳定，与PRNet在侧面视图下的性能相当。
4.5. Running Time and Model Size Comparisons
在表3中：
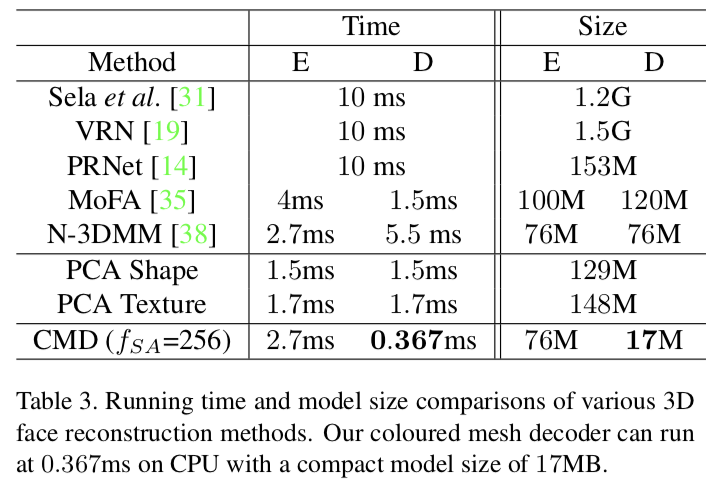
我们比较了多种三维重建方法的运行时间和模型大小。由于有些方法没有公开[31,35,38]，我们只提供了一个大概的估计。Sela等人的[31]、VRN[19]和PRNet[14]都使用了运行时间类似的编码器-解码器网络。然而，Sela等人的[31]需要昂贵的非刚性注册步骤和细化模块。
我们的方法得到一个与N-3DMM[38]和MoFA[35]可比的编码器运行时间。然而，对于形状和纹理，N-3DMM[38]需要通过两个CNNs解码特征。MoFA[35]直接使用线性基，对于28K点解码步骤为约1.5ms的单乘法。相比之下，提出的彩色网格解码器只需要一个高效的网格卷积网络。在CPU (Intel i9-7900X@3.30GHz)上，我们的方法可以在0.367 ms (2500FPS)内完成彩色网格解码，比使用线性形状基更快。我们的非线性彩色网格解码器(17M)的模型大小几乎是MoFA中使用的线性形状基(120MB)的七分之一。最重要的是，上述实验证明我们的非线性网格解码器的容量远远高于线性基。
5. Conclusions
提出了一种基于网格卷积的非线性3DMM方法。我们的方法直接在网格域上解码形状和纹理，具有紧凑的模型大小(17MB)和非常低的计算复杂度(CPU上超过2500 FPS)。在网格解码器的基础上，我们提出了一种图像编码器和一种彩色网格解码器结构，可以直接从自然环境上的二维人脸图像中重建纹理和形状。大量的定性可视化和定量重建结果证实了该方法的有效性。
