Class-Balanced Loss Based on Effective Number of Samples - 1 - 论文学习
https://arxiv.org/pdf/1901.05555.pdf
skewed 倾斜的，歪斜的 heuristic 启发式的 interpolated插值 focal 焦点的 complementary 互补的 coverage 覆盖 tamable 可驯服的 intrinsic 内在的，本质的
Abstract
随着大规模、真实世界数据集的迅速增加，长尾数据分布问题的解决变得至关重要（即少数类占了大部分数据，而大多数类的代表性不足)。现有的解决方案通常采用类重新平衡策略，例如根据每个类的观察数量重新采样和重新加权。在这项工作中，我们认为，随着样本数量的增加，新添加的数据点的额外好处将减少。我们引入了一个新的理论框架来测量数据重叠，方法是将每个样本与一个小的邻近区域联系起来，而不是单个点。有效的样本被定义为样品的体积,可以通过一个简单的公式计算(1−βn) /(1−β),其中n是样本的数量和β∈(0,1)是一个hyperparameter。我们设计了一个权重调整方案，利用每个类的有效样本数来重新平衡损失，从而产生一个类平衡损失。对人工诱导的长尾CIFAR数据集和包括ImageNet和iNaturalist在内的大规模数据集进行了综合实验。我们的结果显示，当使用提议的类平衡损失训练时，网络能够在长尾数据集上获得显著的性能增益。
1. Introduction
深度卷积神经网络(CNNs)最近在视觉识别方面的成功[25,36,37,16]在很大程度上归功于大规模的、现实世界的带注释数据集[7,27,48,40]的可用性。与常用的视觉识别的数据集(例如,CIFAR[24,39],ImageNet ILSVRC 2012[7, 33]和CUB-200 Birds[42]),表现出大致均匀分布的类标签,现实世界的数据集[21]都有着倾斜的分布,有着一条长尾:意思是几个主导类占据大多数例子,而大多数其他的类只有着相对较少的例子。对这些数据进行训练的CNNs在弱表示类中表现较差[19,15,41,4]。
最近的一些研究旨在缓解长尾训练数据的挑战[3,31,17,41,43,12,47,44]。一般来说，有两种策略:重新抽样和成本敏感的重新加权。在重新抽样中，通过对次要类进行过度抽样(添加重复数据)或对主要类进行欠抽样(删除数据)，或两者同时进行，可以直接调整示例的数量。在成本敏感的权重调整中，我们通过将相对较高的成本分配给来自较小类的示例来影响损失函数。在使用CNNs进行深度特征表示学习的情况下，重新采样可能会引入大量的重复样本，从而降低了训练速度；模型在过度采样时容易出现过拟合，或者在欠采样时可能丢弃对特征学习很重要的有价值的样例。由于在CNN训练中使用重采样的这些缺点，本文的工作重点是重新加权的方法，即如何设计一个更好的类平衡损失。
典型地，一个类平衡损失分配样本权值与类频率成反比。这种简单的启发式方法已被广泛采用[17,43]。然而，最近针对大规模、真实世界、长尾数据集的训练工作[30,28]表明，在使用这种策略时，性能很差。相反，他们使用一种“平滑”版本的权值，这种权值根据经验设置为与类频率的平方根成反比。这些观察提出了一个有趣的问题:我们如何设计一个适用于不同数据集数组的更好的类平衡损失?
我们打算从样本容量的角度来回答这个问题。如图1所示：
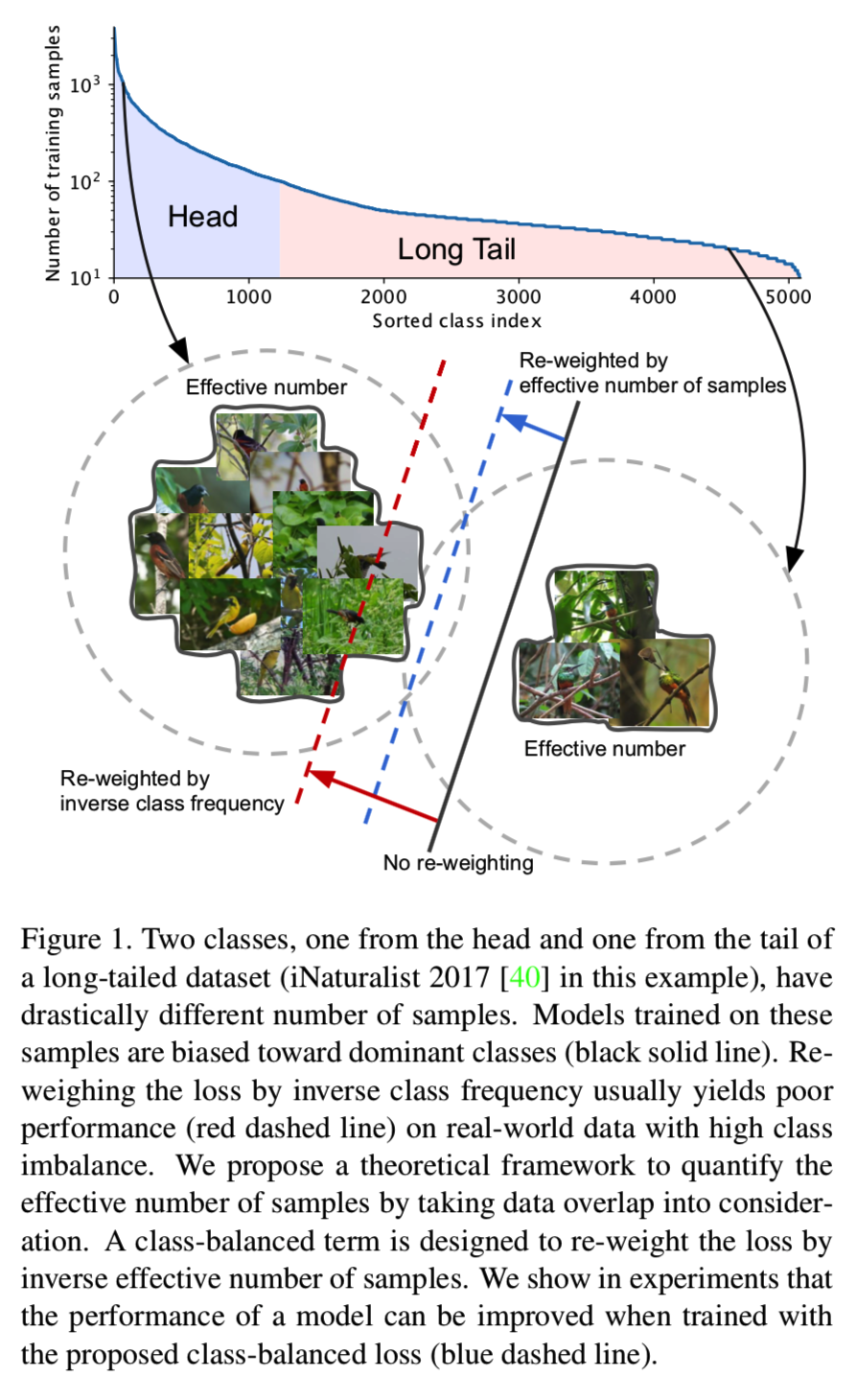
我们考虑训练一个模型来区分来自长尾数据集的主类和次类。由于数据的高度不平衡，直接训练模型或通过反样本数来重新加权损失都不能得到令人满意的结果。直观地说，数据越多越好。然而，由于数据之间存在信息重叠，随着样本数量的增加，模型从数据中提取的边际效益也随之减少。基于此，我们提出了一种新的理论框架来描述数据重叠，并在模型和损失不可知的情况下计算样本的有效数量。在损失函数中加入一个与有效样本数成反比的类平衡权重项。大量的实验结果表明，这个类平衡项显著地提高了长尾数据集上训练CNNs的常用损失函数的性能。
我们的主要贡献如下:(1)我们提供了一个理论框架来研究样本的有效数量，并展示了如何设计一个类平衡项来处理长尾训练数据。(2)我们证明，在现有的常用损失函数(包括softmax cross-entropy, sigmoid cross-entropy和focal loss)中加入所提出的类平衡项可以显著地改善性能。此外，我们证明了我们的类平衡损失可以作为视觉识别的一个通用损失，在ILSVRC 2012上表现优于常用的softmax cross-entropy。我们相信，我们对样本有效数量和类平衡损失的量化研究可以为长尾类分布领域的研究人员提供有用的指导。
2. Related Work
以往对长尾不平衡数据的研究主要分为两种情况:重新采样[35,12,4,50](包括过采样和欠采样)和成本敏感学习[38,49,17,22,34]。
Re-Sampling。过度采样增加了小类的重复采样，这可能导致模型过度拟合。为了解决这个问题，可以从相邻的样本[5]中插入新的样本，或者对较小的类进行合成[14,50]。然而，由于新样本中存在噪声，模型仍然容易出错。有人认为，即使欠抽样会带来删除重要样本的风险，欠抽样仍比过度抽样更可取。
Cost-Sensitive Learning。成本敏感学习可以追溯到统计学中的一个经典方法，称为重要性抽样[20]，在这个方法中，为了匹配给定的数据分布，为样本分配权重。Elkan等人研究了在二分类的情况下，如何分配权重来调整决策边界以匹配给定的目标。对于不平衡的数据集，通常采用逆类频率[17,43]加权或逆类频率的平方根的平滑版本[30,28]。作为基于理论框架的平滑加权的推广，我们关注(a)如何量化样本的有效数量和(b)使用它来重新加权损失。另一项重要的工作是研究样本在损失方面的难度，并将更高的权重分配给hard示例[11,29,8,26]。小类的样本比大类的样本损失更大，因为小类学习的特征通常更差。然而，样本难度与样本数量之间并没有直接的联系。给hard示例分配更高的权重的一个副作用是会关注有害的样本(例如，有噪声的数据或错误标记的数据)[23,32]。在我们的工作中，我们没有对样本的难度和数据分布做任何假设。在实验中利用类平衡项对focal loss[26]进行了改进，证明了该方法与基于样本难度的重加权方法是互补的。
值得一提的是，之前的工作也探索了处理数据不平衡的其他方法，包括将大类学到的知识转移到小类[3,31,43,6,44]，并通过度量学习设计更好的训练目标[17,47,45]。
Covering and Effective Sample Size。我们的理论框架是受到随机覆盖问题[18]的启发，其中的目标是覆盖一个由一系列的i.i.d.随机小集合组成的大的集合。我们通过作出合理的假设来简化第3节中的问题。注意，本文提出的有效样本量与统计中有效样本量的概念不同。有效样本容量用于计算样本相关时的方差。
3. Effective Number of Samples
我们将数据抽样过程表示为随机覆盖的简化版本。关键的思想是将每个样本与一个小的邻近区域联系起来，而不是单个点。给出了计算有效样本数的理论框架和公式。
3.1. Data Sampling as Random Covering
给定一个类，表示该类特征空间中所有可能数据的集合为S。我们假设S的体积为N，且N≥1。表示每个数据是单位体积为1且可能与其他数据重叠的S的子集。将数据抽样过程考虑为一个随机覆盖问题，其中每个数据(子集)从S中随机抽样以覆盖整个S集。抽样的数据越多，S的覆盖越好。采样数据的期望总容量随着数据数量的增加而增加，并以N为界。因此,我们定义:
Definition 1(Effective Number有效数字N)。有效样本数N是样本的期望体积。
样本期望体积的计算是一个非常困难的问题，它取决于样本的形状和特征空间[18]的维数。为了使问题易于处理，我们通过不考虑部分重叠的情况来简化问题。也就是说，我们假设一个新采样的数据只能以两种方式与之前采样的数据交互:要么完全在之前采样的数据集合内部，概率为p，要么完全在外部，概率为1−p，如图2所示。随着采样数据点数量的增加，概率p也会增大。
（即对于一个类的数据有一批有效样本N（有效样本即数据完全不同的，如经过数据增强得到的k张数据只能算一个有效样本），这时候取一个样本，如果与已经采样的数据(灰色)部分有重叠的概率为p，完全不重叠的概率为1-p）
在深入研究数学公式之前，我们将讨论有效样本数量的定义与实际可视数据之间的关系。我们的想法是通过使用更多的类数据点来获取边际收益递减。由于真实世界数据之间的内在相似性，随着样本数量的增加，新添加的样本极有可能是现有样本的近似副本。此外，CNNs通过大量数据增强进行训练，对输入数据进行简单的转换，如随机剪切、重新缩放和水平翻转。在这种情况下，所有的增强样本也被认为与原始示例相同（即增强样本判断为与之前采样的数据重叠的样本，所以完全不同的样本才能算一个有效样本）。据推测，数据增强越强，N（即有效样本数）就越小。样本的小邻域是一种通过数据增强来捕获所有近重复项和实例的方法。对于一个类，N可以看作是唯一原型（即完全不一样的样本）的数量。
3.2. Mathematical Formulation
表示样本的有效数量(期望体积)为En，其中n∈Z>0为样本数量。
Proposition 1(Effective Number有效数字N)。即定义En =(1−βn) /(1−β), β= (N−1) / N。
证明：
我们用归纳法来证明这个命题。
很明显E1 = 1，因为没有重叠。所以E1 =(1−β1)/(1−β)= 1。
现在，让我们考虑一个一般的情况，我们已经抽样n - 1个例子，并即将抽样第n个例子。现在，先前采样的数据的期望体积为En−1，而新采样的数据点与先前采样的数据点重叠的概率为p = En−1/N。因此，第n个样本采样后的期望体积为:
假设En−1 = (1 − βn−1)/(1 − β)保持，那么：
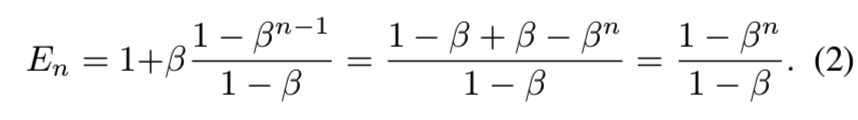
上述命题证明样本的有效数量是n的一个指数函数。超参数β∈(0,1)控制En随着n增长的速度（即抽样的n数量增长，对应能有的有效样本N的数量也跟着增长，β是一个设置的参数，一般设置为[0.9, 1)）
有效数字En的另一种解释是:
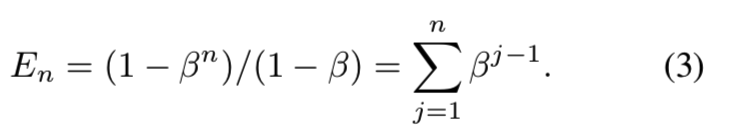
这意味着第j个样本贡献值βj−1到有效数字中。类中所有可能数据的总体积N可以计算为:
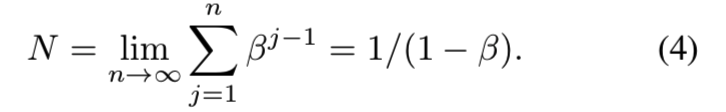
这是符合我们一开始定义的β命题（即β= (N−1) / N）。
推论 Implication1(渐近性质)。如果β= 0 (即N = 1)，则En = 1。如果β→1 (即N→∞)，则En→n。
证明：
如果β= 0,那么En = (1−0n) /(1−0) = 1
如果β→1,设f(β)= 1−βn 和 g(β)= 1−β。取极限得 limβ→1 f(β) = limβ→1 g(β)= 0, 求导g'(β)=−1̸ = 0,
那么取极限 limβ→1 f′(β)/ g′(β) = limβ→1 (−nβn−1) / (−1) = n 存在, 那么使用L’Hoˆpital法则得：
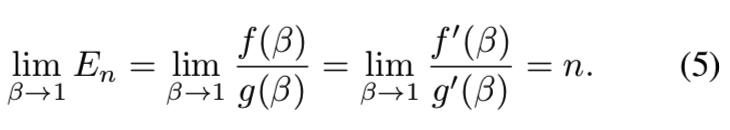
En的渐近性质表明，当N较大时，样本的有效数量与样本的数量n相同。在这种情况下，我们认为唯一原型的数量N较大，因此没有数据重叠，每个样本都是唯一的。（因此当我们有这足够多的训练数据n时，我们就能够认为其的样本有效数量值N=n）
在另一个极端，如果N = 1，这意味着我们相信存在一个单一的原型，所以这个类中的所有数据都可以通过这个原型通过数据增强、转换等来表示。
4. Class-Balanced Loss
上面确定好了样本有效数量N后，接下来就要看怎么将其使用在损失函数中
通过引入一个与样本有效数量成反比的权重因子，设计了类平衡损失来解决从不平衡数据中进行训练的问题。类平衡损失项可应用于大范围的深度网络和损失函数。
对于带有标签labels y∈{1,2，…C}的输入样本x, 其中C是类的总数，假设模型的估计类概率（即模型的输出结果）为 p = [p1, p2,…, pC]⊤, 其中pi∈[0,1]∀i, 我们表示损失函数为 L(p, y)。
假设类i的样本数量为ni,在方程2的基础上, 对于该类i的有效样本数为 Eni =(1−βini) /(1−βi), 其中βi = (Ni−1) /Ni。
如果没有每个类的数据的进一步信息，就很难从经验上为所有类找到一组好的超参数Ni。因此,在实践中,我们假设Ni只是基于数据集的,且对于一个数据集中的所有类来说 Ni= N,βi =β= (N−1) / N。
为了平衡损失,我们引入一个权重因子αi，即与类i的有效样本数量成反比: αi∝1 /Eni。为了在应用αi时使总损失大约在同一规模,我们将归一化αi，使：
为了简单起见,我们使用符号1 /Eni来表示我们的论文的归一化权重因子。
正式地说，对于来自包含ni个样本第i类中采样得到的样本，我们建议增加一个加权
因子(1−β)/(1−βni)到损失函数中,其中超参数β∈(0,1)，其实这个加权因子就是上面的符号1 /Eni。
所以类平衡孙书 (CB)损失可以写成:
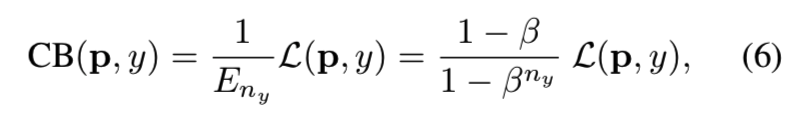
其中ny表示在真实类y中的样本数量。我们在图3可见在不同β的的ny函数中的类平衡损失项：
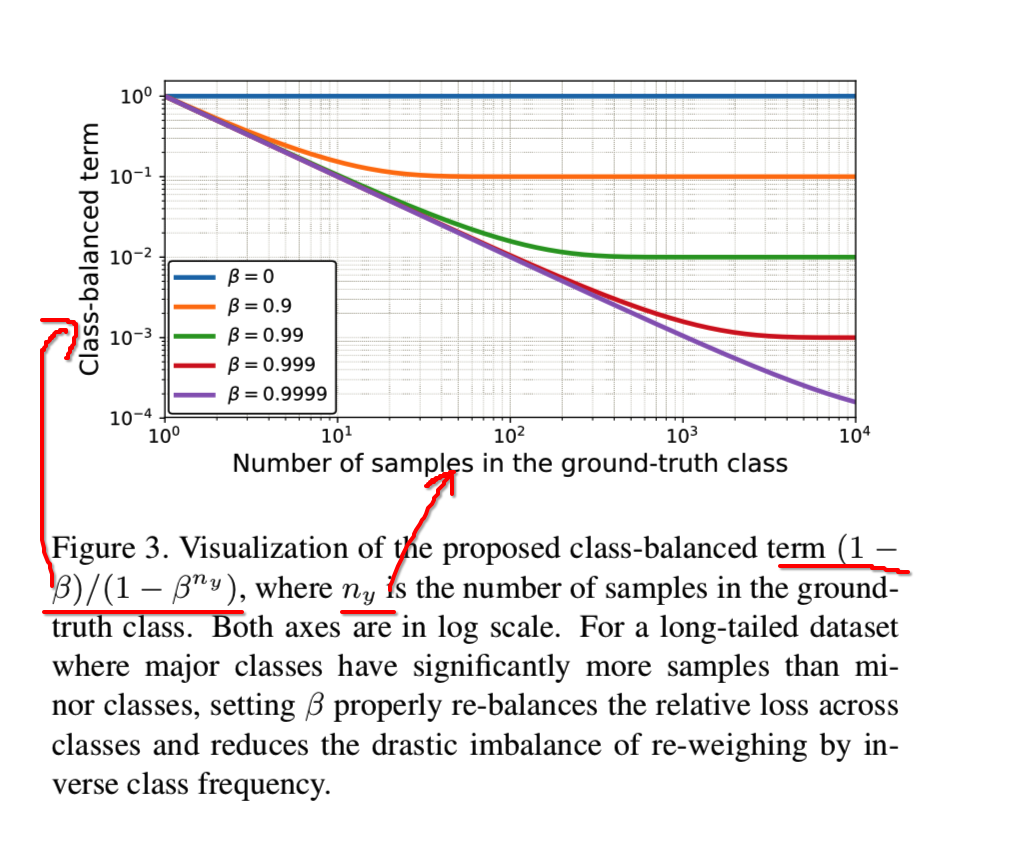
注意,β= 0对应无重新加权 和 β→1对应使用逆类频率进行重新加权。
提出的有效样本数的新概念使我们能够使用一个超参数β顺利调整完全无重新加权和使用逆类频率进行重新加权之间的类平衡项。
提出的类平衡项(1−β)/(1−βny)与模型和损失无关的, 在某种意义上,与损失函数L和预测得到的类概率p是相对独立的。
为了证明该类平衡损失项是通用的,我们将展示如何应用该类平衡损失项到三个常用的损失函数:softmax cross-entropy loss, sigmoid cross-entropy loss和focal loss中。
4.1. Class-Balanced Softmax Cross-Entropy Loss
假设所有类的模型预测输出（即logits）是z=[z1,z2，…，zC]⊤, 其中C为类的总数。softmax函数认为每个类相互排斥，并在所有类上计算概率分布为 
，其中∀i∈{1,2,...,C}。
给定一个类别label为y的样本，该样本的softmax cross-entropy(CE)损失为:
假设类y有ny个训练样本，则类平衡(CB)softmax cross-entropy损失为：
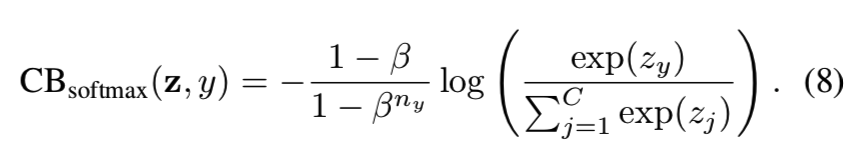
4.2. Class-Balanced Sigmoid Cross-Entropy Loss
与softmax不同的是，sigmoid函数计算的类概率假设每个类是独立的，而不是互斥的。在使用sigmoid函数时，我们将多类视觉识别看作是多个二进制分类任务，其中网络的每个输出节点执行一个vs所有的分类来预测目标类相对于其他类的概率。
与softmax相比，sigmoid对于真实世界的数据集可能有两个优点:(1)sigmoid不假定类之间的互斥性，这与真实世界的数据很好地一致，其中一些类可能彼此非常相似，特别是在大量细粒度类的情况下。(2)由于每个类都被认为是独立的，并且有自己的预测器，所以sigmoid将单标签分类与多标签预测相结合。这是一个很好的属性，因为真实世界的数据通常有多个语义标签。
为简单起见，我们使用与softmax cross-entropy相同的符号，将zit定义为:
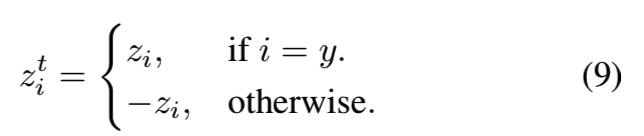
则sigmoid cross-entropy (CE)损失被写成：
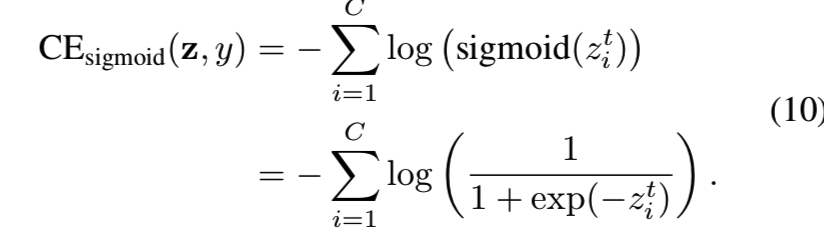
那么类平衡(CB)的sigmoid cross-entropy 损失为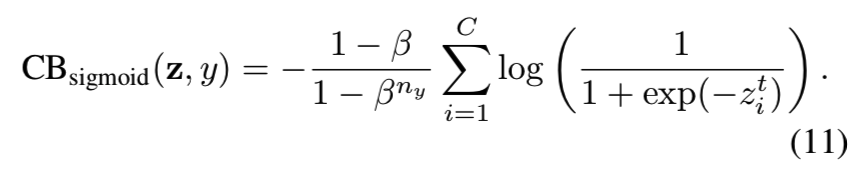
4.3. Class-Balanced Focal Loss
最近提出的focal looss(FL)[26]在sigmoid cross-entropy损失的基础上增加了一个调制因子，以减少分类良好的样本的相对损失，并将重点放在困难样本上。令pit = sigmoid(zit) = 1/(1 + exp(−zit))，focal loss可表示为:
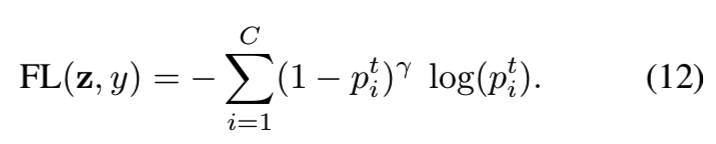
类平衡(CB)的focal loss为：
最初的focal loss是α-balanced变体。类平衡的focal loss是一样是α-balanced损失，其中αt =(1−β)/(1−βny)。因此,类平衡项可以被视为一个在有效的样本数量的概念基础，明确地在focal loss中设置αt的方式。
其实上面三个损失的CB版本就是在原来的式子中增加了一个特定的权重weight
实现可见Class-Balanced Loss Based on Effective Number of Samples - 2 - 代码学习
