Gate Decorator: Global Filter Pruning Method for Accelerating Deep Convolutional Neural Networks - 模型压缩 - 1 - 论文学习
Abstract
过滤器(filter)剪枝是卷积神经网络加速和压缩的最有效方法之一。在这项工作中,我们提出了一种叫做Gate Decorator的全局过滤器剪枝算法,它通过将一个普通的CNN模块的输出乘以通道缩放因子(即gate,代码中为g)来对其进行转换。当比例因子设置为0时,相当于删除相应的过滤器。我们使用泰勒展开来估计由于将比例因子设置为零而导致的损失函数的变化,并使用泰勒展开来估计全局过滤器的重要性排序。然后我们通过移除那些不重要的过滤器来修剪网络。在修剪之后,我们将所有的比例因子合并到原始的模块中,因此没有引入特殊的运算或结构。此外,我们提出了一个迭代剪枝框架称为Tick-Tock,以提高剪枝精度。大量的实验证明了我们方法的有效性。例如,我们在ResNet-56上实现了最先进的剪枝比例,减少了70%的Flops,但没有显著的准确性损失。对于ImageNet上的ResNet-50,我们的修剪模型减少40%的FLOPs,比基线模型多出0.31%的top-1精度。使用多种数据集,包括CIFAR-10、CIFAR-100、CUB-200、ImageNet ILSVRC-12和PASCAL VOC 2011。
1 Introduction
近年来,我们见证了CNNs在许多计算机视觉任务上的显著成就[40,48,37,51,24]。在强大的现代gpu的支持下,CNN模型可以被设计得更大、更复杂以获得更好的性能。然而,大量的计算和存储消耗阻碍了将最先进的模型部署到资源受限的设备上,如移动电话或物联网设备。约束主要来自于[28]的三个方面:1)模型大小。2)运行时内存。3)计算操作次数。以广泛使用的VGG-16[39]模型为例。该模型有多达1.38亿个参数,消耗超过500MB的存储空间。为了推断出一个224×224分辨率的图像,模型需要160多亿个浮点运算(FLOPs)和93MB额外的运行时内存来存储中间输出,这对于低端设备来说是一个沉重的负担。因此,网络压缩和加速方法引起了人们极大的兴趣。
最近关于模型压缩和加速的研究可分为四类:1)量化[34,55,54]。2)快速卷积[2,41]。3)低秩近似[7,8,50]。4)滤波剪枝[1,30,15,25,28,33,56,52]。在这些方法中,滤波器剪枝(又称通道剪枝)因其显著的优点而受到广泛的关注。首先,滤波器剪枝是一种通用的技术,可以应用于各种类型的CNN模型。其次,过滤器修剪不会改变模型的设计理念,这使得它很容易与其他压缩和加速技术相结合。此外,修剪后的网络不需要专门的硬件或软件来获得加速。
神经修剪最早是由Optimal Brain Damage(OBD)提出的[23,10],其中LeCun等人发现,一些神经元可以被删除,但不会造成明显的准确性损失。对于CNNs,我们在过滤层对网络进行剪枝,因此我们将这种技术称为过滤剪枝(如图1)。
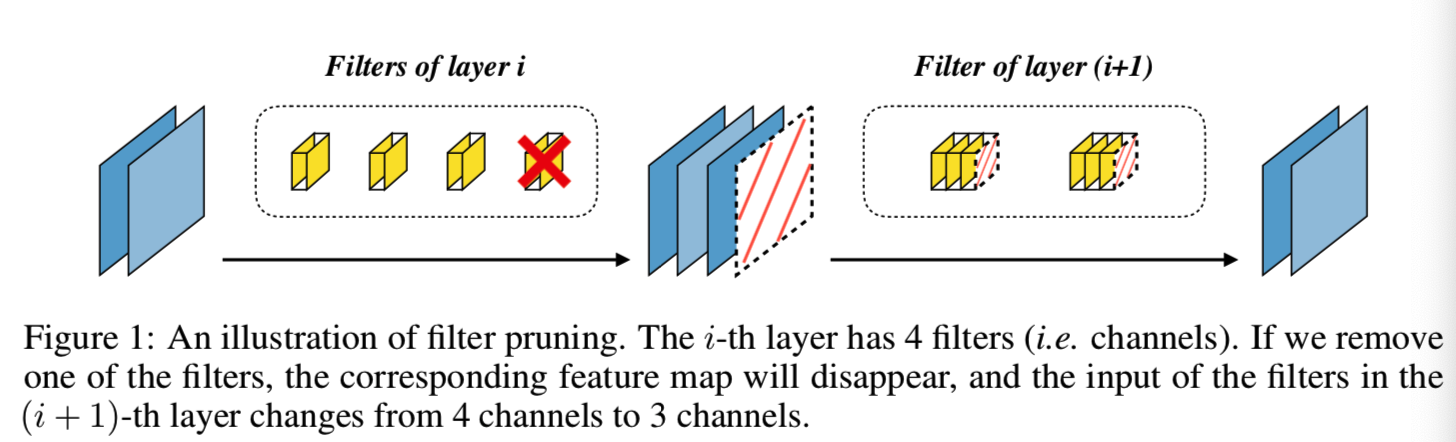
关于过滤器剪枝的研究可以分为两类:1)逐层剪枝[30,15,56]。2)全局修剪[25,28,33,52]。逐层剪枝的方法是每次去除特定层中的滤波器,直到满足一定的条件,然后最小化下一层的特征重构误差。但是一层一层的剪枝过滤器是非常耗时的,特别是对于深度网络。此外,每一层都需要设置一个预定义的剪枝比例,这消除了神经结构搜索中过滤器剪枝算法的能力,我们将在4.3节中讨论。另一方面,全局剪枝方法删除不重要的过滤器,不管它们是哪一层。全局过滤器剪枝的优点是我们不需要为每一层设置剪枝比例。在给定整体剪枝目标的情况下,该算法将揭示所找到的最优网络结构。全局剪枝方法的关键是解决全局滤波器重要性排序问题(GFIR,global filter importance ranking problem )。
在本文中,我们提出了一种新的全局滤波器剪枝方法,它包括两个部分:第一部分是用来解决GFIR问题的Gate Decorator算法。第二个是Tick-Tock剪枝框架,以提高剪枝精度。特别地,我们展示了如何将Gate Decorator应用于Batch Normalization[19],并调用修改后的模块Gate Batch Normalization(GBN)。应该注意的是,由Gate Decorator转换的模块是为了满足修剪的临时目的而设计的。给定一个预先训练的模型,我们将BN模块转换为GBN,然后进行修剪。当修剪结束时,我们将GBN变回普通BN。这样,就不需要引入特殊的操作或结构。大量的实验证明了该方法的有效性。我们在ResNet-56[11]上实现了最先进的剪枝比例,减少了70%的Flops,但没有显著的准确性损失。在ImageNet[4]上,我们减少了40%的ResNet-50[11]的Flops,同时增加了0.31%的top-1准确率。我们的贡献可以总结如下:
我们提出了一个全局的过滤器剪枝管道,它由两部分组成:一部分是用来解决GFIR问题的Gate Decorator算法,另一部分是用来提高剪枝精度的Tick-Tock剪枝框架。此外,我们还提出了group剪枝技术来解决在使用ResNet[11]这样的有shortcut结构的网络进行网络剪枝时遇到的约束剪枝(Constraint Pruning )问题。
(b)实验结果表明,我们的方法优于最先进的方法。我们也广泛地研究了GBN算法和Tick-Tock框架的性质。进一步证明了全局过滤剪枝方法可以看作是一种任务驱动的网络结构搜索算法。
2 Related work
Filter Pruning 。滤波器剪枝是一种很有前途的加速CNNs的解决方案。许多鼓舞人心的作品通过评估它们的重要性来消除这些过滤器。提出了卷积核[25]的大小、零激活函数(APoZ)[17]的平均百分比等启发式度量指标(Heuristic metric)。Luo等人[30]和He等人[15]使用Lasso回归来选择使下一层特征重构误差最小的滤波器。另一方面,Yu等人[52]优化了最终响应层的重构误差,并传播了每个滤波器的重要性评分。Molchanov等人使用泰勒展开来评估滤波器对最终损失函数的影响。另一类作品在一定的限制下训练网络,消除一些过滤器或在其中发现冗余。Zhuang等人通过应用额外的识别感知损耗对预训练模型进行微调,并保留有助于识别能力的滤波器,获得了良好的结果。然而,识别感知损失是为分类任务设计的,这限制了它的使用范围。Liu等人[28]和Ye等人[49]对每个滤波器应用尺度因子,对训练中的损耗增加稀疏约束。Ding等人提出了一种新的优化方法,通过训练使多个滤波器达到相同的值,然后安全地去除冗余滤波器。这些方法需要从头开始训练模型,这对于大型数据集来说非常耗时。
Other Methods 。量化方法通过减少不同参数值的数量来压缩网络。将32位浮点参数量化为二进制或三进制(ternary)。但这些激进的定量策略通常伴随着准确性的丧失。[55, 54]表明,当使用适度的量化策略时,量化网络甚至可以超越全精度网络。近年来,提出了新的卷积设计。Chen等人设计了一个即插即用的卷积单元OctConv,该单元根据混合特征图的频率进行因式分解。实验结果表明,OctConv可以在减少计算量的同时提高模型的精度。低秩分解方法[7,8,5]用多个低秩矩阵近似网络权值。加速网络的另一个热门研究方向是探索网络体系结构的设计。许多计算效率架构[16,36,53,32]被提出用于移动设备。这些网络是由人类专家设计的。为了结合计算机的优势,自动神经结构搜索(NAS)近年来受到了广泛的关注。许多研究已经被提出,包括基于强化学习的[57],基于梯度的[47,27],基于进化的[35]方法。值得注意的是,我们提出的Gate Decorator算法与本小节中描述的方法是正交的(orthogonal)。也就是说,Gate Decorator可以与这些方法相结合,以实现更高的压缩和加速率。
3 Method
在本节中,我们首先介绍Gate Decorator (GD)来解决GFIR问题。并展示如何将GD应用于Batch Normalization[19]。然后,我们提出了一个迭代剪枝框架称为Tick-Tock,以更好的剪枝精度。最后,我们介绍了组剪枝技术来解决在使用shortcuts(即resnet网络等)进行网络剪枝时遇到的约束剪枝问题。
3.1 Problem Definition and Gate Decorator
形式上,令L(X, Y;θ)表示用于训练模型的损失函数,其中X是输入数据,Y是相应的标签,θ是模型的参数。我们用K表示网络中所有过滤器的集合。过滤器修剪是选择一个子集的过滤器k⊂K,从网络删除它们对应的参数θk−。我们注意到左边参数θk+即剪枝后剩下的参数,因此我们有θk+∪θk−=θ。为了最小化损失的增加,我们需要通过解决以下优化问题来仔细选择k:
![]()
其中,||k||0是k的元素数,解决这个问题的一个简单方法就是尝试k的所有可能,选择对损失影响最小的最佳。但它需要计算||k||0次 ∆L =|L(X, Y);θ)−L(X, Y);θk+)| 来完成一次迭代的修剪,这是不可行的深模型,其有着成千上万的过滤器。为了解决这一问题,我们提出了Gate Decorator来有效地评估过滤器的重要性。
假设特征映射z是k滤波器的输出,我们让z乘以一个可训练的比例因子φ∈R和使用zˆ=φz进行进一步的计算。当gate φ为零,它相当于修剪过滤器k。利用泰勒展开式,我们可以大约评估修剪的∆L。首先,为了符号方便,我们在等式(2) 重写∆L, 该式子中的Ω包括X, Y和所有除了φ以外的模型参数。因此LΩ(φ)是一个一元函数w.r.t φ。
![]()
然后使用泰勒公式在等式(3)和(4)中扩展LΩ(0)

连接等式(2)和(4),可以得到:
![]()
R1是拉格朗日余数,我们忽略这一项因为它需要大量的计算。现在,我们可以基于式(5)求解GFIR问题,在反向传播过程中,这个问题很容易计算。每个过滤器ki∈K,我们使用等式(6)计算了Θ(φi),即过滤器的重要性分数,D是训练集:
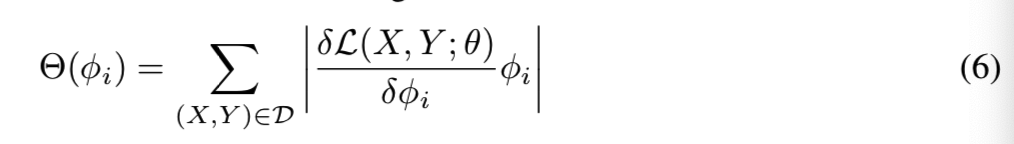
特别地,我们将Gate Decorator应用到Batch Normalization[19]中,并将其用于我们的实验。我们将修改后的模块Gate Batch Normalization称为GBN。我们选择BN模块有两个原因:1)BN层在大多数情况下跟随卷积层。因此,我们可以很容易地找到滤波器和BN层的特征映射之间的对应关系。2)我们可以利用BN中的比例因子γ为φ提供排名线索(有关详细信息,请参阅附录A):

GBN 定义在等式(7)中,φ⃗是φ的向量,c是zin的通道大小:
![]()
此外,对于不使用BN的网络,我们还可以直接将Gate Decorator应用于卷积。Gated卷积的定义见附录B:

3.2 Tick-Tock Pruning Framework
在本节中,我们引入了一个迭代剪枝框架来提高剪枝的准确性,该框架被称为Tick- tock(图2)。
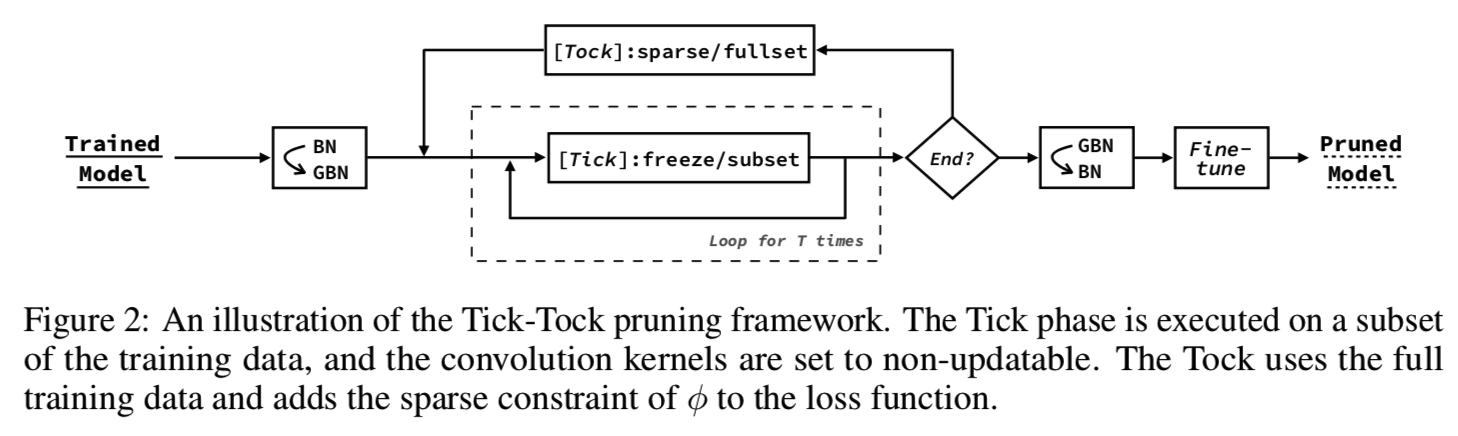
Tick步骤设计用来获得如下的目标:
1)加速剪枝过程
2)计算每个过滤器的重要性得分Θ
3)修复之前修剪造成的内部协变量移位问题[19]
在Tick阶段,每个epoch中我们使用训练数据的一个子集来训练模型,我们只允许gate φ和最后的线性层是可更新的,以避免在小数据集中发生过度拟合。重要性分数Θ根据等式(6)在向后传播中计算。训练后,我们使用重要性得分Θ排序所有的过滤器,并删除部分最不重要的过滤器。
Tick阶段可以重复T次,直到进入Tock阶段。Tock阶段的目的是对网络进行微调,以减少由于删除过滤器而导致的错误积累。除此之外,对φ的稀疏约束将添加到训练期间的损失函数中,这有助于揭示了不重要的过滤器和计算Θ更准确。Tock中使用的损失函数如式(8)所示:
![]()
最后,我们对修剪后的网络进行微调以获得更好的性能。Tock步骤和Fine-tune步骤有两个不同之处:1)Fine-tune通常比Tock训练更多的epochs。2)Fine-tune不向loss函数添加稀疏约束。
3.3 Group Pruning for the Constrained Pruning Problem
ResNet[11]及其变体[18、46、43]包含shortcut连接,它将元素明智地添加到由两个剩余块生成的特征映射上。如果我们单独对每一层的过滤器进行修剪,可能会导致shortcut连接中特征映射的不对齐。
若干解决办法被提出。[25,30]绕过这些麻烦的层,只修剪残差块的内层。[28,15]在每个残差块的第一个卷积层之前插入一个额外的采样器,不修剪最后一个卷积层。然而,避免麻烦层的方法限制了修剪比例。此外,采样器解决方案为网络添加了新的结构,这将引入额外的计算延迟。
为了解决这一问题,我们提出了组剪枝的方法:将由纯shortcut connection 连接的GBNs分配给同一组。纯shortcut connection是侧支上没有卷积层的快捷方式,如图3所示:
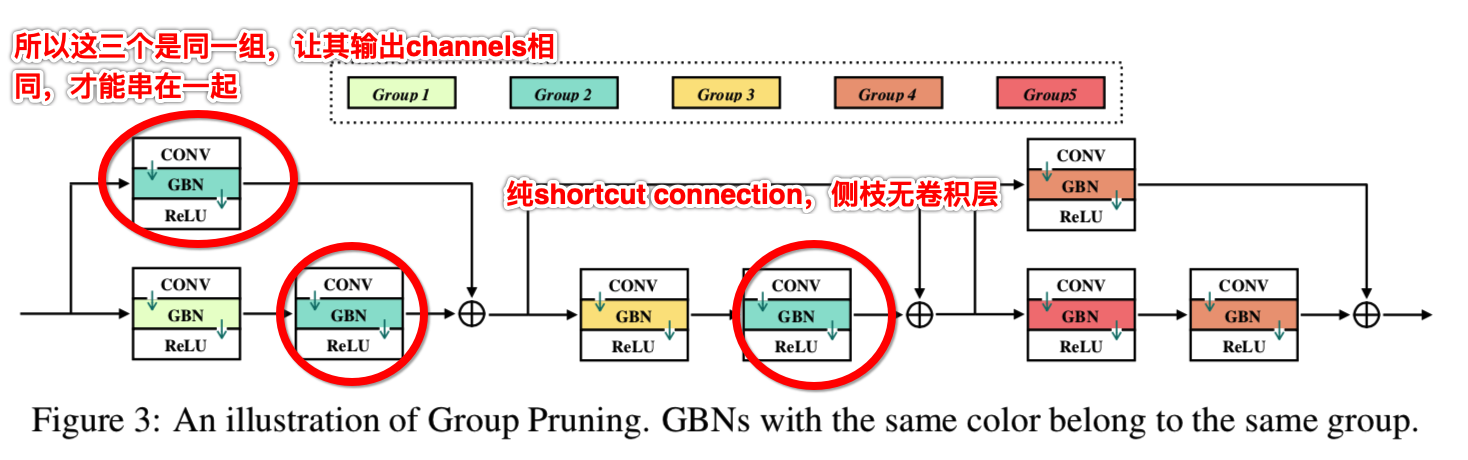
一个组可以被看作是一个虚拟的GBN,它的所有成员共享相同的修剪模式。一个组中过滤器的重要性分数是其成员的总和,如等式(9)所示:

g是在组G中GBN成员之一,在组G中所有成员中排名第j的过滤器的重要性分数定义为Θ(φjG)。
3.4 Compare to the Similar Work.
PCNN[33]也使用泰勒展开来解决GFIR问题。
所提出的Gate Decorator与PCNN在三个方面有所不同:
1)由于没有引入尺度因子,PCNN通过对其特征图中每个元素的一阶泰勒多项式求和来评估滤波器的重要度得分,这会累积估计误差。
2)由于缺少尺度因子,PCNN无法利用稀疏约束。然而,根据我们的实验,稀疏约束对于提高剪枝精度起着重要的作用。
3)跨层的分数标准化对于PCNN是必要的,但对于Gate Decorator则不是。这是因为PCNN使用累加的方法来计算重要度分数,这会导致分数的尺度随特征图的大小而跨层变化。我们放弃了分数标准化,因为我们的评分是全局可比的,而标准化将引入新的估计错误。
4 Experiments
省略
5 Conclusion
在这项工作中,我们提出了三个组件来服务于全局过滤器修剪的目的:
1)Gate Decorator来解决全局过滤器重要性排序(GFIR)问题。
2) Tick-Tock框架,提高修剪精度。
3)group剪枝法解决约束剪枝问题。
我们证明了全局过滤器剪枝方法可以看作是一个任务驱动的网络结构搜索算法。大量的实验表明,该方法优于目前几种最先进的滤波剪枝方法。



