异常检测-基于孤立森林算法Isolation-based Anomaly Detection-1-论文学习
论文http://202.119.32.195/cache/10/03/cs.nju.edu.cn/da2d9bef3c4fd7d2d8c33947231d9708/tkdd11.pdf
1. INTRODUCTION
异常是与正常样例有着不同的数据特性的数据模式。检测异常的能力具有重要的相关性,异常经常在多种应用领域中提供关键和可操作的信息。比如在信用卡交易中能够显示信用卡的使用有欺诈行为;在天文图像中的异常点能够说明发现了新的星星;一个不正常的计算机网络流量模式能够代表(stand for)一个为授权访问。这些应用需要用着高检测精度和快执行效率的异常检测算法。
很多现存的异常检测方法,包括基于分类的方法[Abe et al. 2006; Shi and Horvath 2006]、Replicator神经网络(RNN)[Williams et al. 2002]、one-class SVM[Tax and Duin 2004]和基于聚类的方法[He et al. 2003],都是构造一个正常样例的大概描述,然后认证异常是那些不符合正常描述的样例。这些异常检测方法基本上都是一种算法的“副作用”或副产品,这种算法最初设计的目的不是为了异常检测(例如分类或聚类)。这将会导致两种主要的后果:
- (i)这些方法不能有效地检测异常——结果就是,这些方法经常导致过多的错误警告(即将正常样例认证为异常),或者是检测出来的异常过少;
- (ii)很多现存的方法都限制使用在低维数据和小的数据大小中,这是其最初算法的历史遗留问题。
该论文提出了一个通过隔离样例,不依赖于任何距离和密度措施的检测异常的不同方法。为了达到这个目的,我们推荐的方法利用了两个异常的本质特性:
- i)它们是少量的,仅包含少数样例;
- ii)它们有着和其他正常样例不同的属性值。总之异常是“少且不同的”,这让她们能够很好地被隔离机制检测出来。
无论如何,隔离机制能够被用来隔离样例。我们选择使用称为隔离树(iTee)的二进制数结构,其能够有效地构造来隔离样例。因为隔离的易测性,异常通常更可能被隔离在靠近iTree的根部的地方;然而正常点则更可能被隔离在iTree的深处。这就形成了我们用于检测异常的方法的基础理念。虽然这是一个十分简单的机制,但是我们展示在这篇论文中的是一个集高效和准确性为一体的检测异常的方法。
该推荐方法叫做孤立森林(iForest, Isolation Forest),根据给定的数据集构建一个iTree;异常就是那些在iTrees中有着短的平均路径长度的样本。在该方法中有着两个训练参数和一个评价参数:训练参数是构建的树的数量以及子采样的大小;评估参数是在评估时树的高度限制。我们说明了iForest的检测精度能够在少量树中快速收敛;它仅需要一个小的子采样大小就能够获得一个高效且高检测精度的结果;不同的高度限制用来迎合不同密度的异常集。
除了上面说的使用隔离作为检测异常的方法的主要不同之处外,iForest与现存的基于模型的 (e.g. [Abe et al. 2006; He et al. 2003])、基于link的(e.g. [Ghoting et al. 2004])、基于深度的 (e.g. [Rousseeuw and Leroy 1987])、基于距离的 (e.g. [Knorr and Ng 1998])以及基于密度的(e.g. [Breunig et al. 2000]) 方法有着很大的不同,如下所示:
- 隔离树的特性使得它能够子采样到一定长度,这是现有方法中没有的灵活度(更多的细节将提供在5.5中)
- iForest不使用距离和密度措施来检测异常。这将减少在所有基于距离和密度方法中的大量距离计算损失
- iForest有着线性的时间复杂度,且带有少量的常量和内存需求;它是一种训练时间和空间复杂度恒定的算法。据我们所知,现有方法中性能最好的方法只能获得近似线性的时间和空间复杂度[Angiulli and Fassetti 2009]。
- iForest能够扩展去解决极大数据量和有着大量不相关属性的高维问题(可见5.6部分)
该论文仅关注用于多变量数据异常检测的无监督、无参数方法,且仅关注于连续性数据。我们假设数据集中的所有属性都等价用于异常检测,在该论文中并不解决条件异常问题[Song et al. 2007]
该论文的结构如下:
- 第二部分阐述了使用一个iTree递归地对数据进行分区来实现隔离
- 第三部分比较了隔离、密度和距离方法去理解他们结构化的不同
- 第四部分提供了构造iTrees和iForest的算法。一个基于iTrees的新异常分数概念被提出。使用子采样大小和评估高度限制来处理数据中出现的遮挡和淹没问题(即数据之间过于相似的情况)
- 第五部分经验性地将iForest与4个先进的异常检测方法进行比较;同时分析iForest的检测性能:
- 在不同参数下的性能
- 在聚集异常数量增长情况下的性能(即数据有遮挡情况下)
- 在异常和正常数据点之间的距离减小情况下的性能(即数据有淹没的情况下)
- 当数据是高维时
- 当训练样本中没有异常数据的情况下
- 第六部分调查了相关工作
- 第七部分描述了未来可能需要进行的工作
- 第八部分即总结
从文章 [Liu et al. 2008a]的初始版本进行扩展,我们使用额外的阐述和新的在 3, 4.5, 5.2, 5.3, 5.4, 5.5, 5.7, 6, 7 部分以及A, B, C, D和E附录中找到的材料来丰富了第二部分的内容
2. ISOLATION AND ISOLATION TREES
介绍隔离和隔离树概念
在该论文中,术语“隔离”意味着“从剩下的样例中分离样本”。通常来说,一个基于隔离的方法度量了单个样例的易隔离性;异常即那些有着高易隔离性的样例。为了实现隔离的想法,,我们提出能够自然隔离数据的数据结构。在样例能够被递归分区的随机生成二进制树中,这些树能够为异常生成明显的更短的路径,有两种情况能实现短路径:
- 该区域被异常所占据时,少的异常导致一个更少数量的分区——在树结构中即更短的路径,即因为异常数量很少,这个分区的路径一定很快就结束二分叉;
- 有着可区分的属性值的样本更可能在分区过程中被更早地分离出来
因此,当森林中的每个随机树都为一些独特点共同生成更短的路径长度时,那么这些特殊点就很有可能是异常点
在图1(a)和2(b)中,我们观察到一个正常点xi通常需要进行更多次地分区才能够被隔离出来。与此相反的则是异常点x0则仅仅需要少量的分区就能够被隔离出来
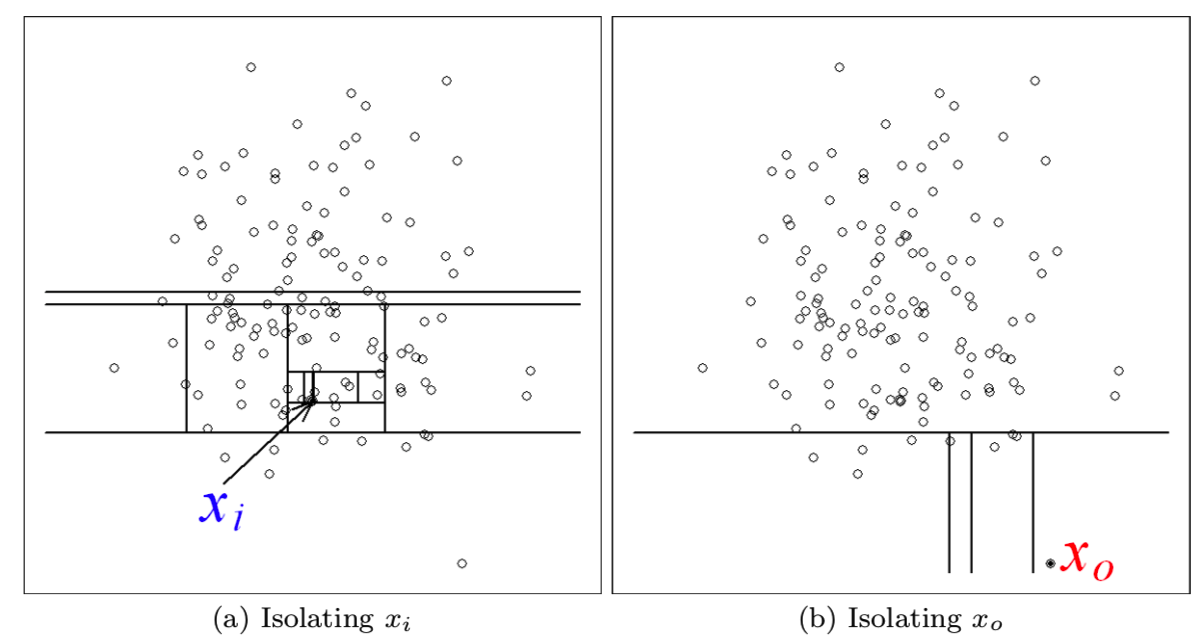
在该例子中,分区是通过随机选择一个属性值,然后随机选择该属性值最大和最小值之间中的一个值作为分割值(split)来生成的。当递归分区能够通过一个树结构来表示时用于隔离一个点需要的分区数量等于从根节点到终端节点的路径长度遍历。在该例子中,xi的路径长度是比x0的路径长度大的。
当每一个分区随机生成后,带着不同分区集的独立树也就生成了。然后平均所有树的路径长度去得到期望的路径长度值。图1(c)显示了x0和xi在树的数量增长的情况下收敛的平均路径长度:
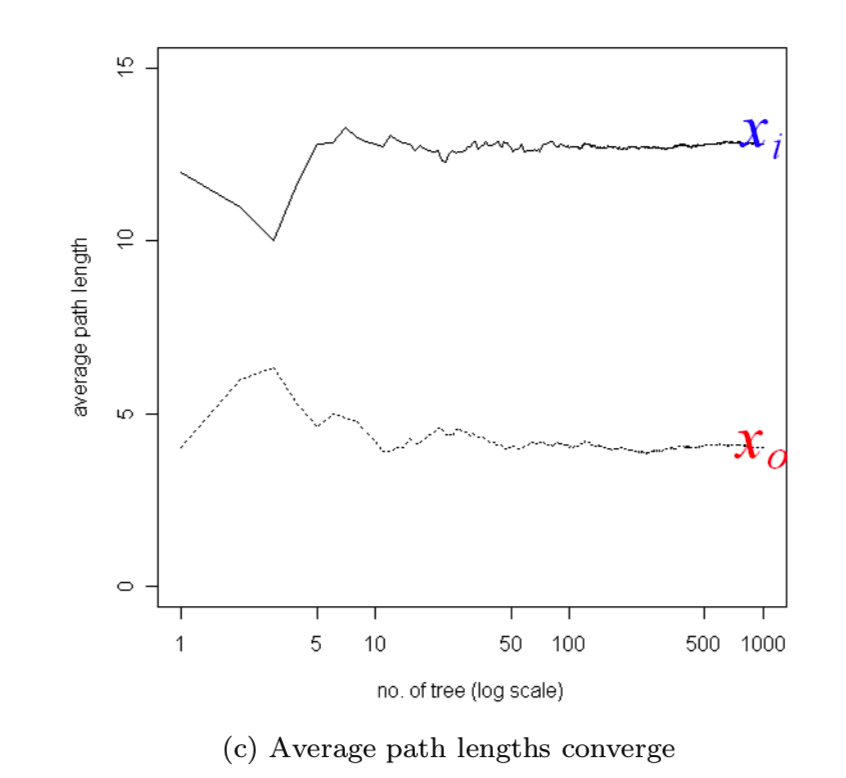
可见当使用1000棵树时,x0和xi的平均路径长度分别收敛到了4.0和12.8。可见异常需要的路径长度是比正常点需要的路径长度要短的。
除了可上面所示的检测分散的外围异常点的情况,iForest也能够检测那种异常被正常数据包围的情况。如图2就阐述了一种正常点形成了一个环形,而异常数据处在这个环形的中间而不是外面的这种情况:
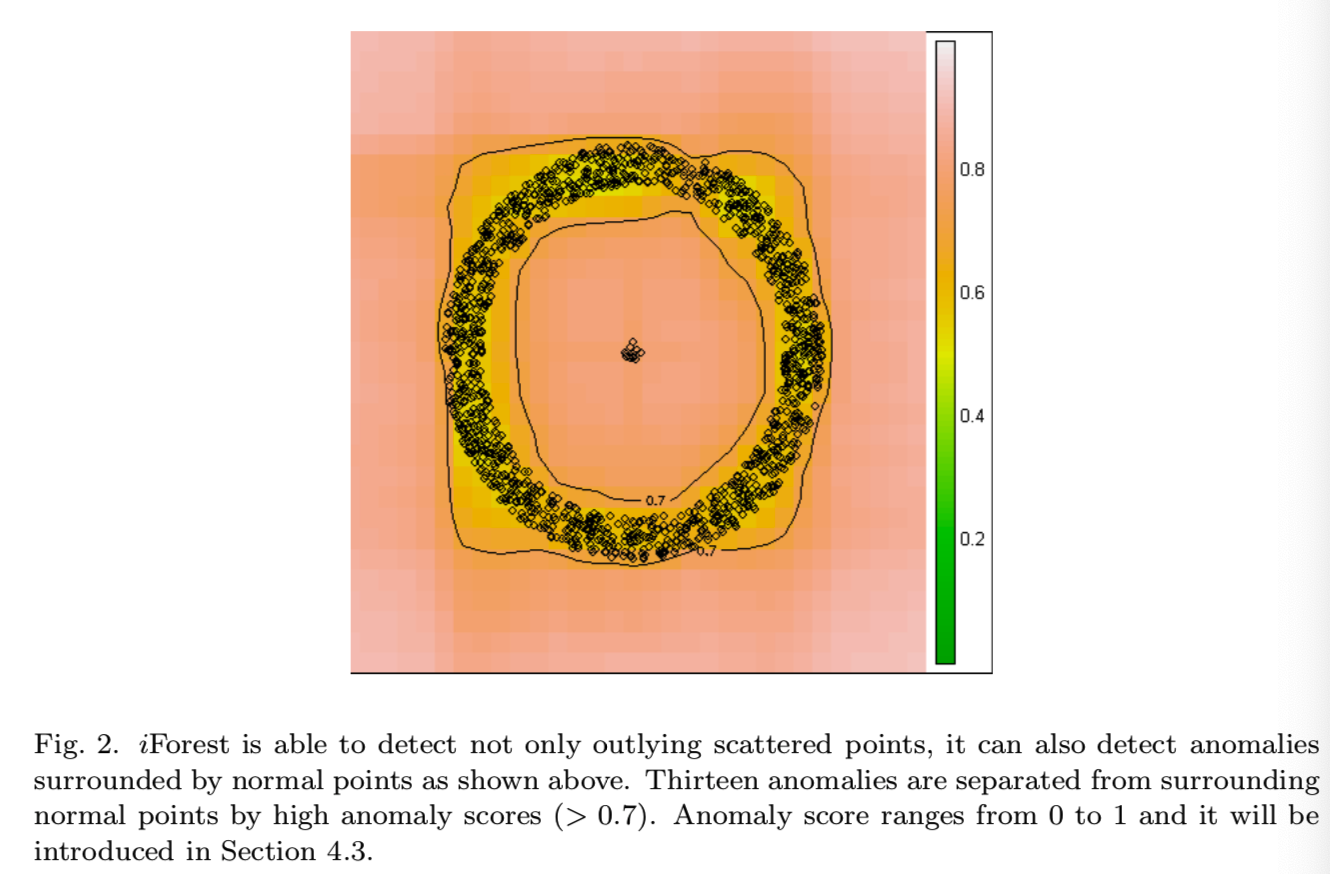
一个带着两条来自iForest的0.7异常分数等高线的异常分数等高线图如上所示,可见异常点的异常分数是高于0.7的(颜色发橘),而正常数据则是低于0.7的(颜色发黄)。异常分数的公式将会在4.3部分说明
Definition : Isolation Tree。定义T为隔离树的节点。T即可能是没有孩子节点的外部点,也可能是带着test的有着两个孩子节点(Tl, Tr)的内部节点。节点T上的test包含一个属性q和该属性的分割值p,比如通过 q<p 测试(test)来决定该数据点是往左Tl 还是往右Tr。
定义X={x1, ... , xn}为给定的d维分布的数据集。有Ψ个样本的采样X'属于X被用来构建一个隔离树(iTree)。我们通过随机选择一个属性q和一个该属性的分割值p来递归地划分X',直到:
- 剩下的节点中只有一个样本,不能再划分
- 或剩下的样本都有相同的值
这两种情况才停下来。iTree是一个恰当的二叉树,树中的每一个节点都要么有0个或两个孩子节点。假设所有样本都是可区分的,在一个iTree完全生成时,每一个样本都被隔离为一个外部节点(即没有孩子节点),在这种情况下外部节点的数量为Ψ,而内部节点的数量为Ψ-1,这样该iTree的节点总数为2Ψ-1;因此需要的内存是有边界的,并且仅是样本数量Ψ的线性增长。对于符号和注释的定义可以参考下面的表1:

异常检测的任务是提供一个能够反射异常程度的排序。使用iTrees,检测异常的方法就是根据它们的平均路径长度来排序数据点;异常数据则是那些排在列表前面的数据点。定义路径长度的方法如下所示:
Definition : Path Length 一个点x的路径长度h(x)是通过从一棵iTree的根节点遍历到一个外部节点经过的边界数量。
我们使用路径长度作为隔离敏感性程度的测量:
- 短的路径长度表示高的隔离敏感性
- 长的路径长度表示低的隔离敏感性
iTree的概率解释可在附录A中找到
3. ISOLATION, DENSITY AND DISTANCE MEASURES
介绍隔离和基于密度、长度方法的差别
在该论文中,我们断言基于路径长度的隔离方法是比基本的密度和长度测量方法更适合用于异常检测任务的。
使用基本的密度测量,其假设是“正常点出现在密集区域,而异常点出现在稀疏区域”。使用基本的距离测量方法,其基本假设是“正常点和其邻居相邻,而异常点则远离其邻居”[Chandola et al. 2009]
但也有违反这些假设的情况,如高密度和短距离并不总是意味着正常样本;同时低密度和长距离也不总是意味着异常样本。当密度和距离在局部上下文中测量时,通常情况下,得到的密度高或距离短的点在整个数据集的全局上下文中可能是异常的。可是在基于路径长度的方法中就不会出现这样的模糊性,我们将会在接下来的三个段落中阐述该内容
在基于密度的异常检测中,异常被定义为在低密度区域中的数据点。密度通常被测量为:
- k近邻的平均距离的倒数
- 给定固定半径中的点的数量
在基于距离的异常检测中,异常被定义为远离其他点的数据点。基于距离的异常分数的两种常用定义方式为:
- kth最近邻的距离
- kth最近邻的平均距离[Tan et al. 2005]
这种密度和距离测量方法的一个缺点在于没有办法去处理带有不同密度区域的数据集。同时,对于这些用来检测密度异常聚类的方法,k必须比最大异常聚类的大小大。这就造成了一个搜索问题:即找到最合适的k值。注意一个大的k值将大幅增加计算
表面上,隔离测量方法的函数和密度、长度测量方法相似,比如隔离将分散的外部点排得比正常点高。可是我们发现基于路径长度的隔离在有着不同分布的数据下有着与密度、长度测量方法不同的表现。在图3中,异常点在左边,而正常聚集点则在右边。路径长度、密度(k-nn)和kthnn距离值被分别点在图3(a)和3(b)中。在密度和距离估计中使用k=10。在图3(a)中密度值显示了异常点有着高密度,而正常聚集点有着低密度:
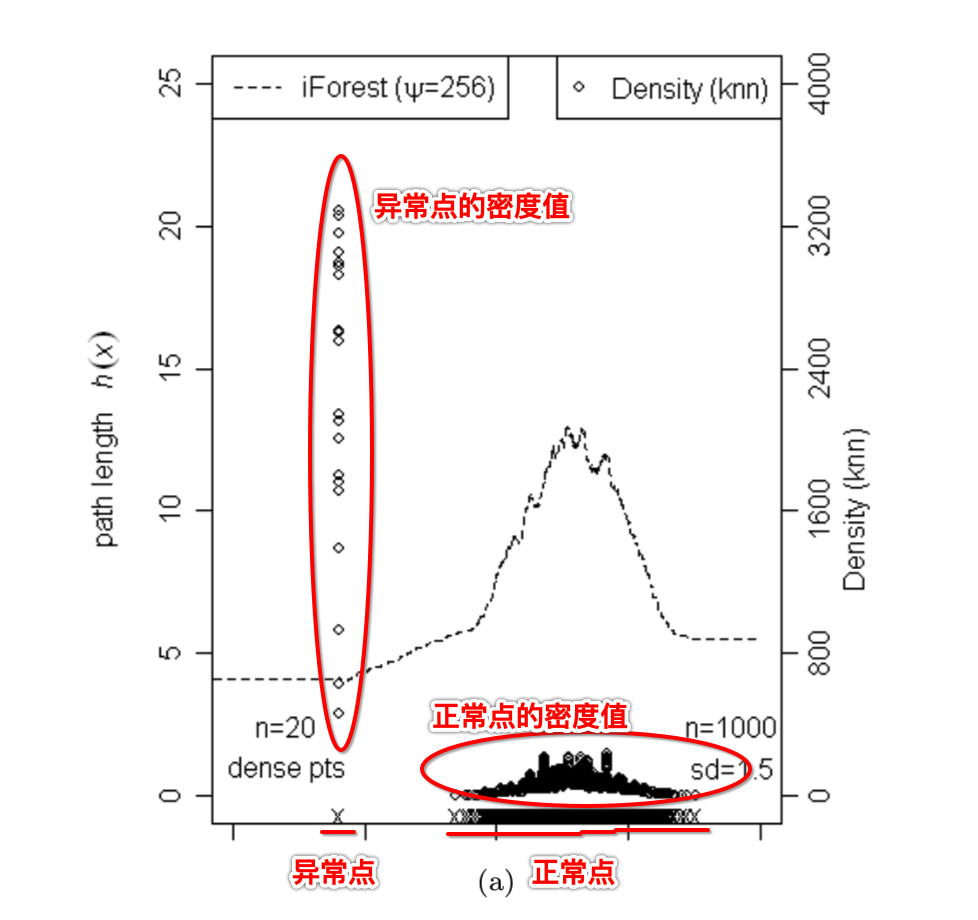
在图3(b)中kthnn距离值显示了异常点有着短距离,而正常聚集点有着相对大一点的距离:
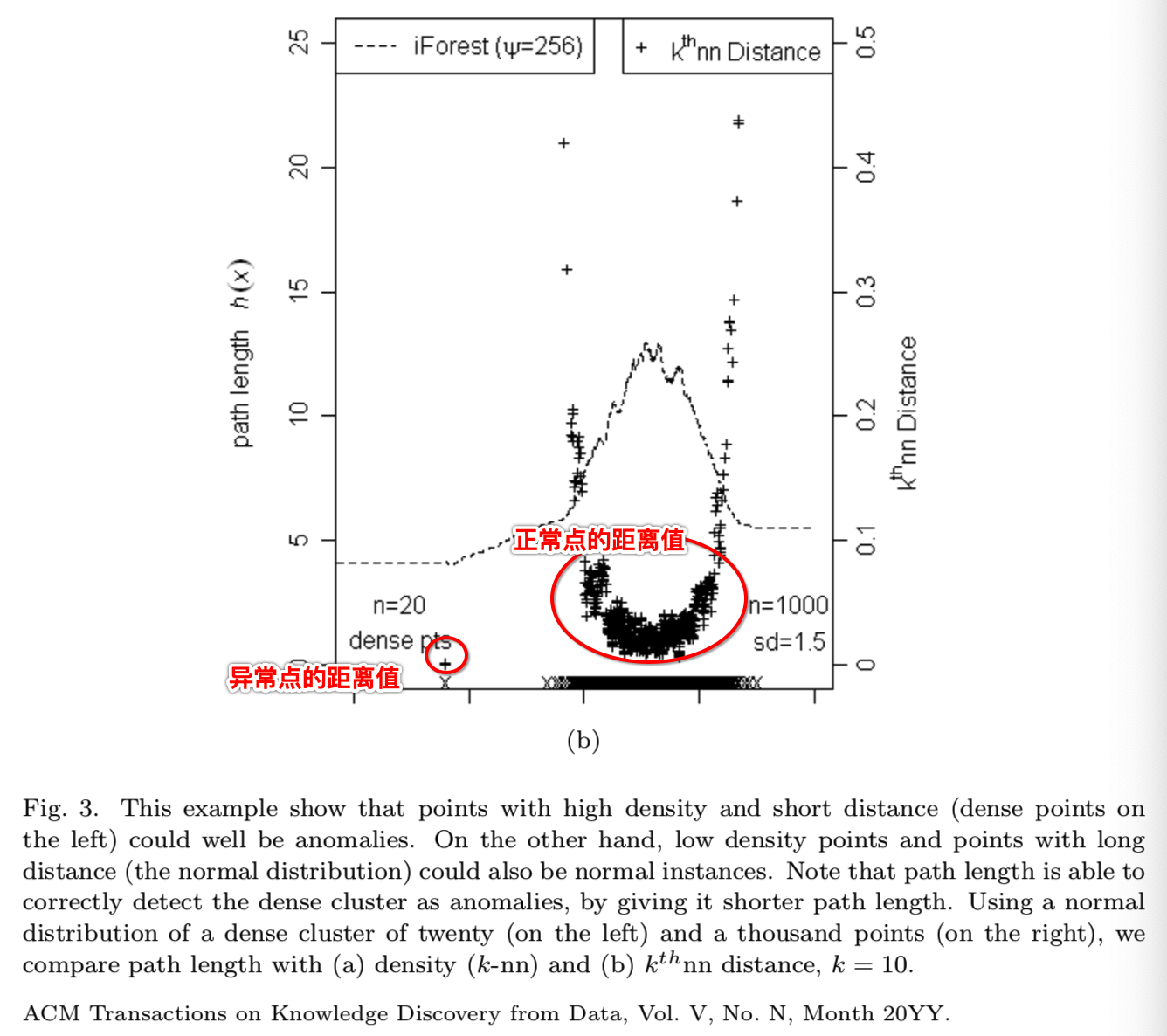
该基于距离和密度的结果与我们的期望是相反的。但是路径距离就能够通过给隔离的密集点更短的路径距离来解决这个问题。主要的原因是路径长度是在自适应的上下文中生成的,每个分区的上下文都是不同的从第一个分区(根节点)有着整个数据集的上下文,到最后一个分区(叶子节点)则有着局部数据点的上下文信息。可是密度(k-nn)和kthnn距离仅关注着k个邻居(局部上下文),并没有将整个数据集的上下文考虑进来
总之,我们对比了这三个用于检测异常的基本方法;即基于隔离、密度和长度的方法。我们发现基于隔离(路径长度)的测量方法能够检测聚集和分散的异常;然而密度和长度方法只能检测分散的异常。有很多用来加强基本密度和长度测量的方法,隔离方法更好是因为在检测聚集和分散的异常时不需要对基础的测量方法进行调整,更简单。
4. ANOMALY DETECTION USING IFOREST
如何使用iForest实现异常检测
在该部分将描述iForest机制的细节以及对异常检测有意义的异常分数公式。同时我们将会解释为什么使用更小的子采样将能够带来更好的隔离模型,同时通过调整评估高度限制来测试检测效果的变化
使用iForest异常检测是一个两个阶段的过程:
- 第一个是训练阶段,使用从给定训练集中子采样的样本集来构建隔离树
- 第二个是评估阶段,传递测试样例到隔离树中来获得每个样本的异常分数
4.1 Training Stage
在训练阶段,通过递归分区一个子样本X'来构建iTrees,直到所有样本都被隔离。训练阶段的细节能够见下面的算法1和2。每一个iTree都是用一个从X中无放回随机选择的X'构造而成
算法1:

- 即先从整个数据集X中采样大小为ψ的子样本X'
- 然后使用该子样本构建隔离树iTree,并将其放入Forest列表中
- 循环进行上面两个步骤,直到生成的iTree的数量满足t
在算法1中可见iForest算法有着两个输入。即子采样集的大小Ψ和树的数量t;该参数的影响将在下面说明:
subsampling size ψ控制训练数据的大小。我们发现当ψ增加到某个期望的大小时,Iforest的检测结果就是可信赖的了,不需要再继续增加,因为继续增加只会增加运行时间和内存大小,并不会提高检测的精确度。如我们假设异常是“少且不同的”,正常数据则是“多且相同的”。在这个假设下,对于iForest来说,一个小的子采样大小就足够用于从正常数据中区分异常了
按经验来说,我们发现将ψ设置在2^8或256大小就足够在一个大的数据范围内实现异常检测了。除非具体说明,我们在实验中都将ψ=256作为默认值。对子采样大小的影响的分析可见5.5部分,其将展示检测性能在默认设置中接近最优值,并在一个大范围的ψ值中不敏感。
Number of trees t控制集合大小。我们发现路径长度通常在t=100时收敛得最好。除非具体说明,我们在实验中都将t=100作为默认值。
在训练过程的最后,树的集合将返回并准备用于评估。最糟糕情况下训练一个iForest的的时间复杂度为O(tψ2),空间复杂度为O(tψ)
算法2:

即算法1中构造树的详细内容:
- 如果X'满足了上面说的不能够继续下分的两种情况,那就说明到了叶子结点,将该集合的大小|X'|作为size值输入exNode生成一个外部结点,返回向上递归
- 否则就进行分割,随机从d维的属性集Q中选择一个属性q,然后随机在该属性的最大、最小值中选取一个分割值p,样本中属性q的值 < p的,就分为左节点Xl;q的值 >= p的,就分为右节点Xr,然后构建一个中间节点inNode,同时继续对生成的左节点Xl和右节点Xr向下递归
- 重复上述的过程直至都没有可再分的样本集X'
4.2 Evaluation Stage

该算法即计算测试样例x在iTree树T上的路径长度:
- 首先先查看此时的节点是否为外部节点或路径长度e是否已经超出了定义的高度限制hlim。如果是外部节点,则说明已经遍历到了x样本属于的分区,返回此时的e即其路径长度;如果e已经大于或等于定义的高度限制hlim,则返回e+c(T.Size)作为该样例x的路径长度
- 否则就查看此时的分割属性T.splitAtt,并赋值给a,如果样本x的该属性值xa小于该分割属性的分割值T.splitValue,则遍历到该内部节点的左子树;如果xa大于该分割属性,则遍历到该内部节点的右子树,然后循环进行这两步操作,直到返回路径长度值
在评估阶段,就想在算法2中实现的一样,单一的路径长度h(x)是通过计算样本x遍历整个iTree,从根节点到外部节点经过的路径e的数量。当遍历到了预先定义好的高度限制hlim时,返回的路径长度 = e + 调整的c(Size) (c(.)定义在下面的式子1中)。该调整用于估计随机子树的平均路径长度,该子树可以使用超过树高限制的Size数据构建。当为集合的每个子树都计算得到了x在这些子树上的路径长度h(x)后,其异常分数就能够计算了。异常分数和调整的c(Size)将在下面进行定义。
该评估阶段最糟糕情况下的时间复杂度为O(ntψ),n为测试数据大小
4.3 Anomaly Score
对于任何的异常检测方法,异常分数都是需要的。从h(x)生成该分数的难度在于iTree的最大可能高度随着Ψ的值一起增长,平均高度随着logΨ的值一起增长 (即对于一个包含Ψ条记录的数据集,其构造的树的高度最小值为log(Ψ),最大值为Ψ-1)。当从不同采样大小的模型中要求可视化或者比较路径长度时,用上述任何一项(即logΨ或Ψ)对h(x)进行归一化要么不是有界的,要么就是不能直接比较。因此为了实现上述的目的,就需要一个归一化的分数

当iTrees有着和二叉搜索树(BST)有着等价的结构时,对外部节点终端进行的平均h(x)的估计就等价于在BST中的不成功搜索。在这里我们借用BST的分析去估计iTree的平均路径长度。对于一个有着Ψ个样本的采样集,[Preiss 1999]论文的10.3.3部分给出了在BST中不成功搜索的平均路径长度计算:
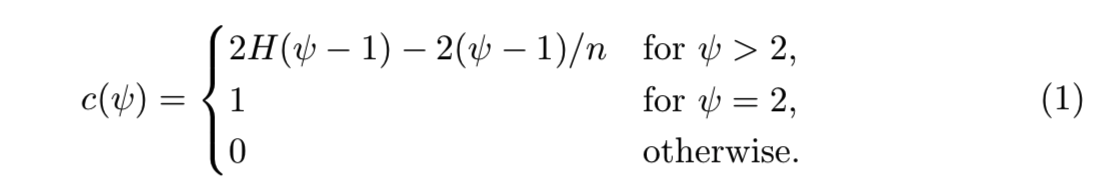
其中H(i)是谐波数( harmonic number),能够通过计算ln(i) + 0.5772156649(欧拉常量)来估计该值。c(Ψ)是给定的Ψ的h(x)的均值,使用它来归一化h(x),因此一个样本x的异常分数定义为:
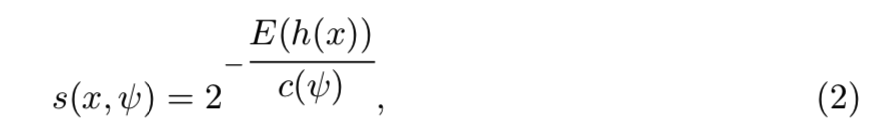
E(h(x))是iTrees集合的h(x)均值。如下条件提供了三种异常分数的特殊值:

即当整个iTrees集合的h(x)均值(即E(h(x)))为0时,则说明该样本x一定是异常点,所以s=1;如果 E(h(x))=Ψ-1,则说明该样本x一定是正常点,所以s=0;如果 E(h(x))=c(Ψ),则说明该样本x并不是很易于区别,所以s=0.5。
图4阐述了E(h(x))和s之间的相关性,s的范围为[0,1], h(x)的范围为[0,Ψ-1]:
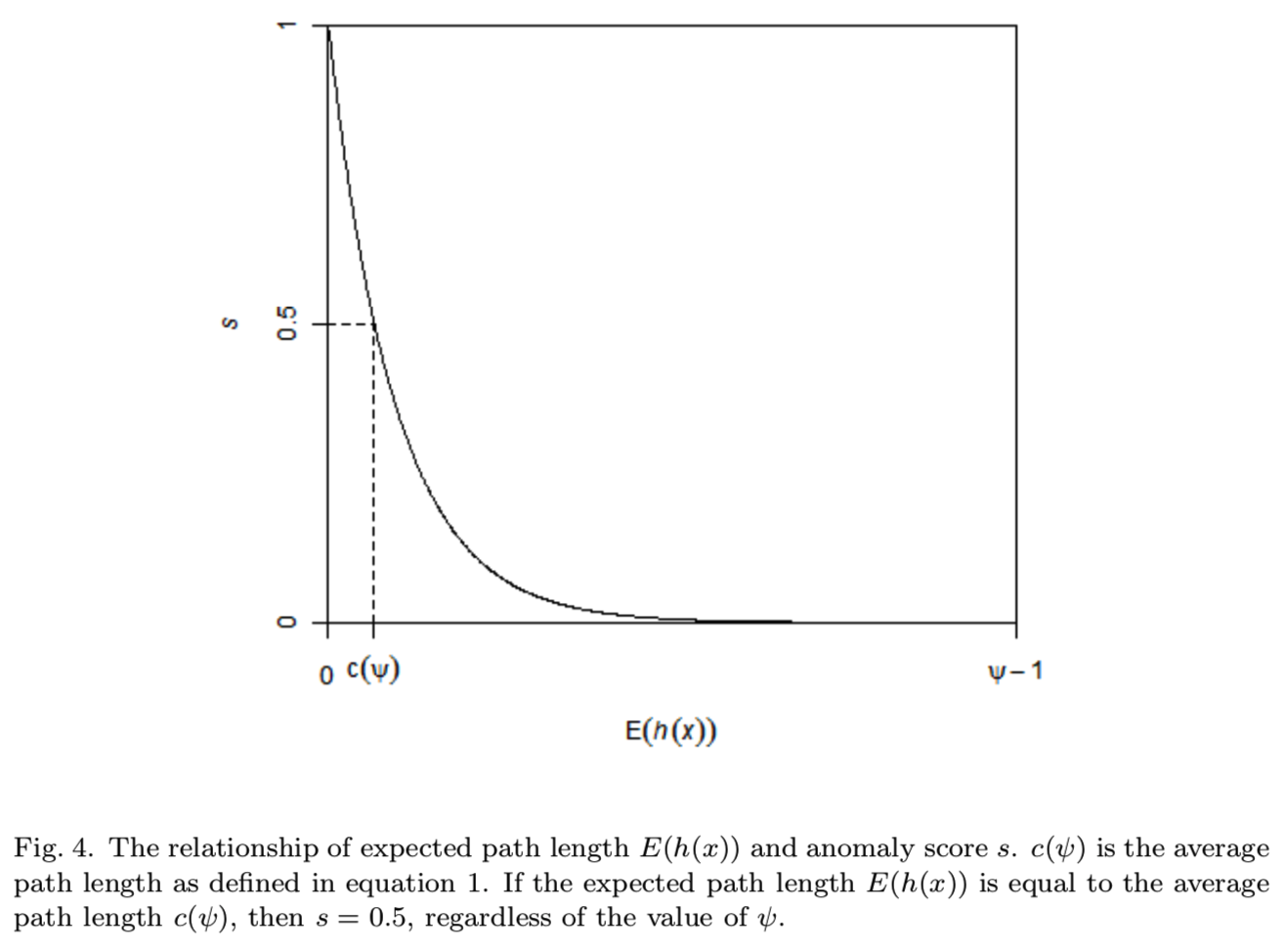
使用异常分数s,我们能够进行以下的判定:
- 如果样本返回的s接近于1,则其一定是异常
- 如果样本返回的s远远小于0.5,则能够认为其为正常样本
- 如果所有的样本返回的s都约等于0.5,则说明整个数据集都没有明显的异常值
通过传递一个格点样本给iForest得到异常分数的等高线,便于对检测结果进行详细分析。图5显示了一个这样的等高线的例子,为了可视化和判别样本空间中的异常:
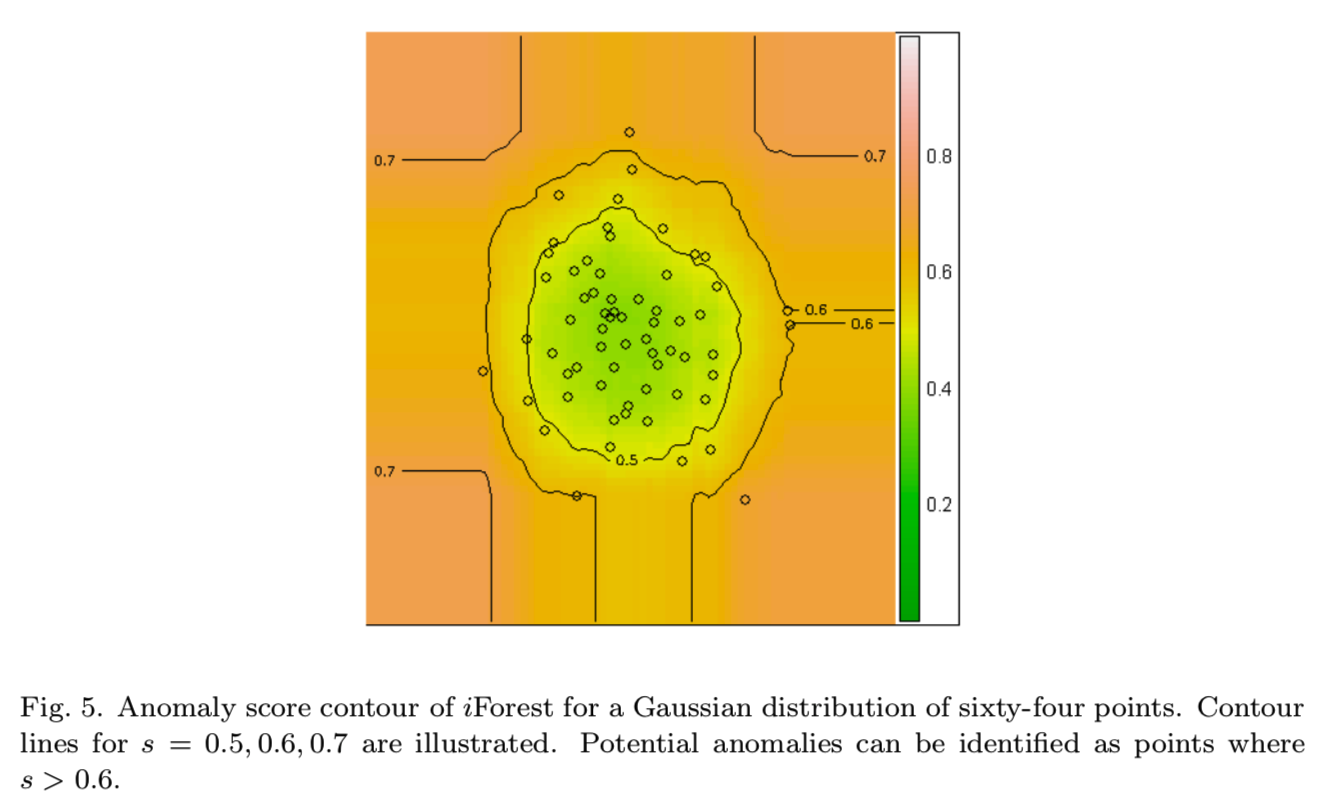
使用等高线能够清楚地识别3个点,当s大于0.6时,就是一个潜在的异常点
4.4 Small Sub-samples Build Better Isolation Models
说明小的子采样大小能够构建更好的隔离模型
淹没和遮挡问题在异常检测[Murphy 1951]中被全面地研究了。
淹没提及的情况为正常数据被错误判定为异常。它出现在正常样本数量增加或正常样本变得分散了的情况下。
另一方面来说,遮挡则是因为存在过多的异常,遮挡了它们自身的存在,让它们无法被判断为异常。它出现在异常聚类变得更大和更密集了。在这种情况下,很多异常检测就会崩溃。注意无论时淹没效应或遮挡效应都是用于异常检测的数据过多导致的。
iForest能够通过使用多个子采样构建模型去减少淹没和遮挡效应。我们发现没有有着小的大小的子采样将能够构建一个比使用来自整个数据集构建的iTree更好的性能。这是因为子采样有着更少被异常点干扰的正常点;这样就使得异常更容易被检测
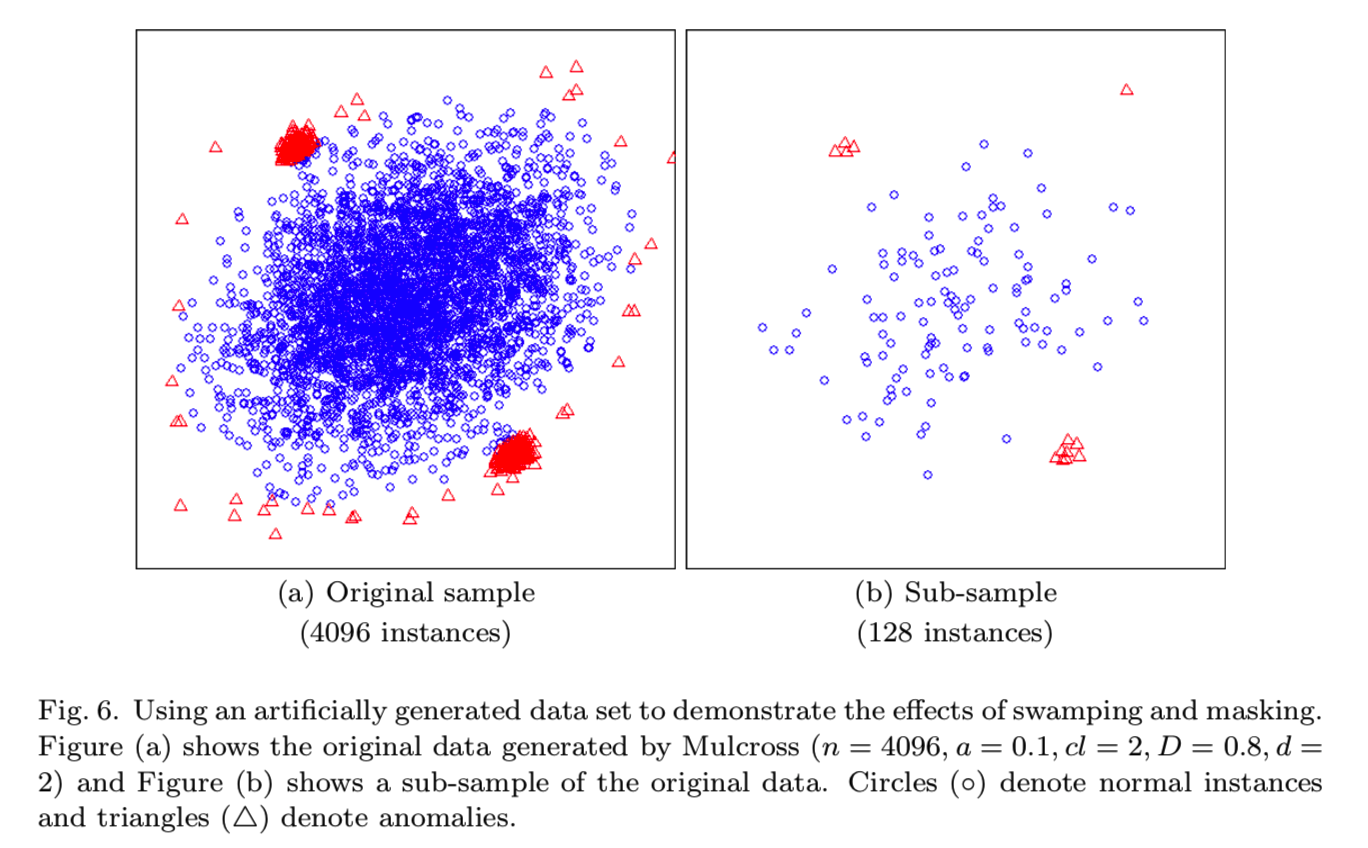
为了阐述子采样是如何减少淹没和遮挡效应的,图6(a)展示了一个通过Mulcross数据生成器生成的 [Rocke and Woodruff 1996],有着4096个样本的数据集。我们故意设置两个相当大且密集并且与正常点的大聚集点很接近的异常聚集点来阐述淹没和遮挡效应。有干扰的正常点分布在异常聚点的周围,该异常聚点比正常聚点还有密集。图6(b)展示了一个来自原始数据的有着128个样本的子采样。可见异常聚集点在子样本中能够很好地被识别出来。那些围绕在两个异常聚集点的“假的”正常样本将会导致淹没效应,这些正常样本将会被清除;在图6(a)中的异常聚集点的数据大小将导致遮挡效应,子采样后将会变小,如在图6(b)中展示的那样。最终的结果是,它们使异常集群更容易分离。
当使用在图6(a)中的整个数据集时,iForest的AUC为0.67。当使用子采样为128或256时,iforest的AUC分别达到0.91和0.83。结果表明,iForest通过显著减少子样本,在处理淹没和遮挡效应方面表现优异。请注意,即使在子采样下,异常仍然比正常点更密集,如图6(b)所示;而且它们仍然能够逃避基于距离和密度的检测方法。在下一小节中,我们将看到iForest如何利用评估高度限制来进一步处理密集的异常集群。
4.5 Adjusting the Granularity of Anomaly Scores
在异常检测中,需要做的一个决定是否一个隔离数据聚集点是不正常的或其周围的数据集是不正常的。在该部分中展示了孤立森林方法能够通过在评估阶段改变树的高度限制来检测这两种情况。注意,在评估阶段调整高度限制并不会改变训练后的模型,也不需要对模型进行重新训练。使用Mulcross数据生成器生成的数据集,在图7中所示,表示两个使用不同高度限制得到的异常分数等高线,即hlim = 1和6。生成的数据具有一个稀疏的集群,比一个小的密集集群(在右上角)大得多。可以注意到,在较高的高度限制,即hlim = 6中,大、小集群周围的散点的异常分数均高于两个集群的核心点。在这种情况下,大集群和小集群周围的散点都被认为是异常:

当hlim = 1时,整个小而密的集群的异常分数较高,被认为是异常。使用较低的高度限制的效果可以描述为降低异常分数的粒度,较高的高度限制提供较高的粒度来检测数据集群周围的分散点。该粒度的改变带来了检测密集异常的优势,详情可见5.3:

在iForest的正常使用中,默认的评估高度限制为最大值,即Ψ-1,因此异常分数有着最高的粒度(即密集的点可能会被检测为正常点)。除了特殊说明,评估树高度将设置为最大值
我们描述了使用iForest进行异常检测的过程——通过隔离实现异常检测,给出了一种基于路径长度的有意义的异常评分公式。我们还分析和解释了为什么iForest使用较小的子采样大小能够产生更好的性能模型,并在评估阶段通过调整树高限制提供了不同级别的检测粒度。
5. EMPIRICAL EVALUATION
本节详细介绍了用于评估iForest的7组实验的结果,并与4个最先进的异常检测器进行了比较。第5.1节给出了本节中使用的数据集。在5.2节中,我们提出了两个用于基准评估的实验。在第一个实验中,我们使用两个已知的统计数据集来验证每个检测器的异常检测能力。实验验证了这些探测器的性能。在第二个实验中,我们使用12个数据集来将iForest与其他检测器进行了比较,这些数据集以前曾用于评估文献中的异常检测器。在5.3节中,第三个实验研究了所有异常探测器在增大异常集群大小的情况下,由于遮挡作用而产生的崩溃特性。研究了不同的评估的高度限制及其对iForest崩溃特性的影响。在5.4节中,第四次实验研究了异常接近法线点(沼泽效应)时,由于沼泽化而引起的击穿特性。在第5.5节中,第五个实验研究了不同的子样本大小对iForest的影响。这些结果为应该使用何种子采样大小及其对检测性能的影响提供了一些见解。我们还证明了当子样本大小和总体大小固定时,训练时间复杂度是恒定的。在第5.6节,第六次实验研究了iForest处理高维数据的能力;我们使用一个简单的单变量测试来减少树构造之前的属性空间。我们的目的是找出这个简单的机制是否能够提高iForest在高维空间的检测性能。在许多情况下,异常数据很难获得;在第5.7节中,第7个实验检验了iForest在只有正常实例可供训练时的性能。
在所有的实验中,都报告了实际CPU时间和Area Under Curve(AUC)。所有数据点的异常值均用于AUC计算。AUC等于异常检测器在异常点分数高于正常点分数时的概率。由于AUC是独立于cutoff点的,所以不管数据集中有多少异常,它都可以测量探测的准确性。在我们实验中的AUC值都是通过在R语言中的一个标准的性能分析包“ROCR” [Sing et al. 2005]进行计算的。用于异常检测的计算AUC的过程将放在附录中。所有的实验都是在Linux集群中以2.3GHz处理单线程作业的方式进行的。
使用在实验中的四个先进的异常检测算法为ORCA、one-class SVM、LOF和Random Forest方法
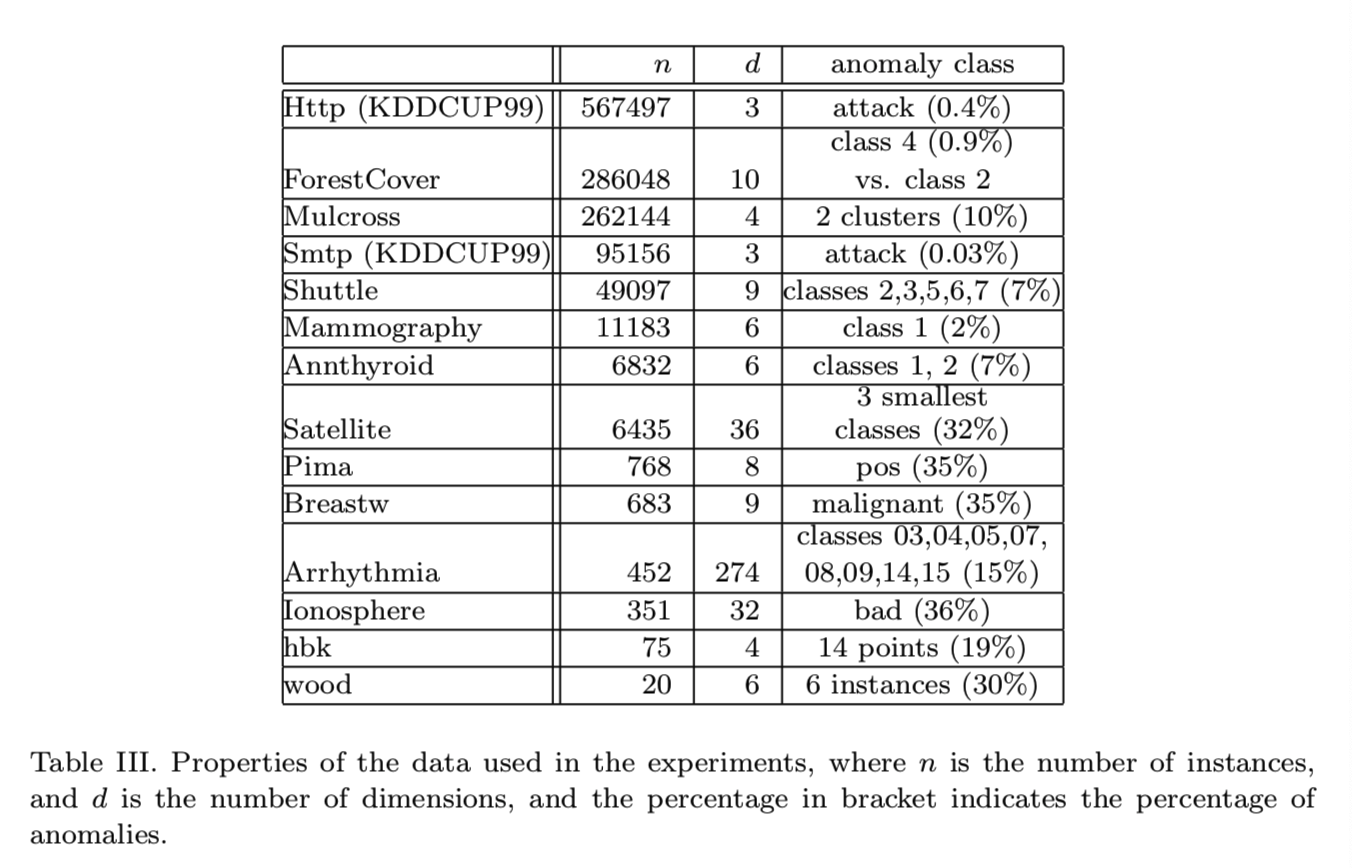
5.1 Data Sets
忽略
5.2 Empirical Comparison of iForest, ORCA, SVM, LOF and Random Forests
本小节由两个实验组成。在第一个实验中,我们使用两个以前使用过的统计数据集hbk和wood (Rousseeuw和Leroy 1987)来检验每个异常检测器的基本行为。在第二个实验中,我们根据AUC和处理时间来评估每个检测器的性能。
Statistical data sets.我们的第一个统计数据集是hbk数据集,它包含75个实例,其中14个是异常。异常由两个小的集群组成,其中一个集群比另一个集群更分散。图8显示了来自5个异常检测器的前20个异常,以及由原来的4个属性建立的由前两个主要成分画成的图。结果表明,iForest和RF是仅有的两个将所有异常排在首位的探测器:
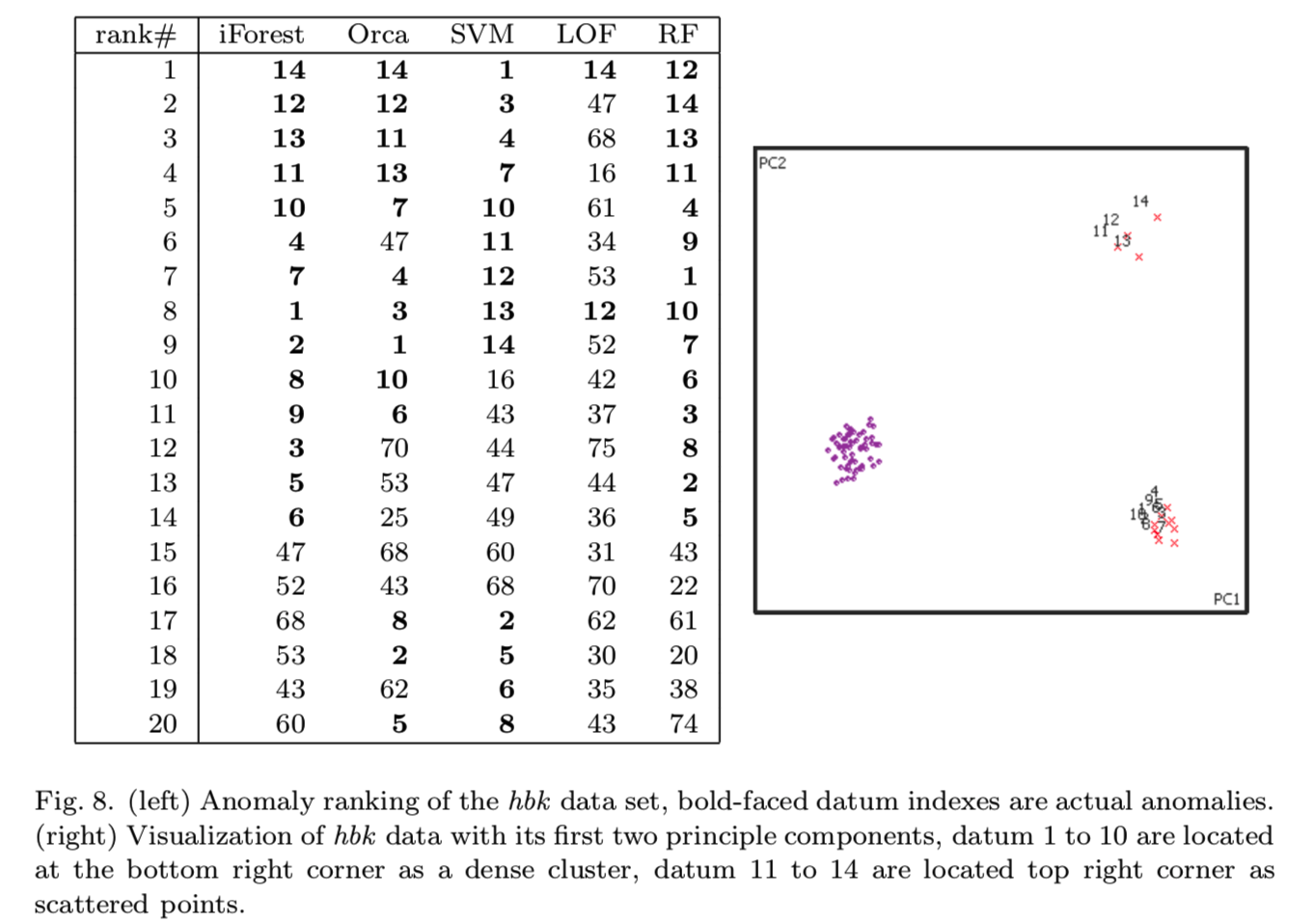
我们的第二个统计数据集是wood数据集,它由20个实例组成,其中6个是异常。异常都在一个较小的集群中。图9显示了所有异常检测器排列的前10个实例,以及由原始6维属性中的两个主要成分画成的二维图。ORCA和LOF正确地识别了所有四个异常,而iForest错误地排列了一个实例,RF在这个数据集中表现很差:
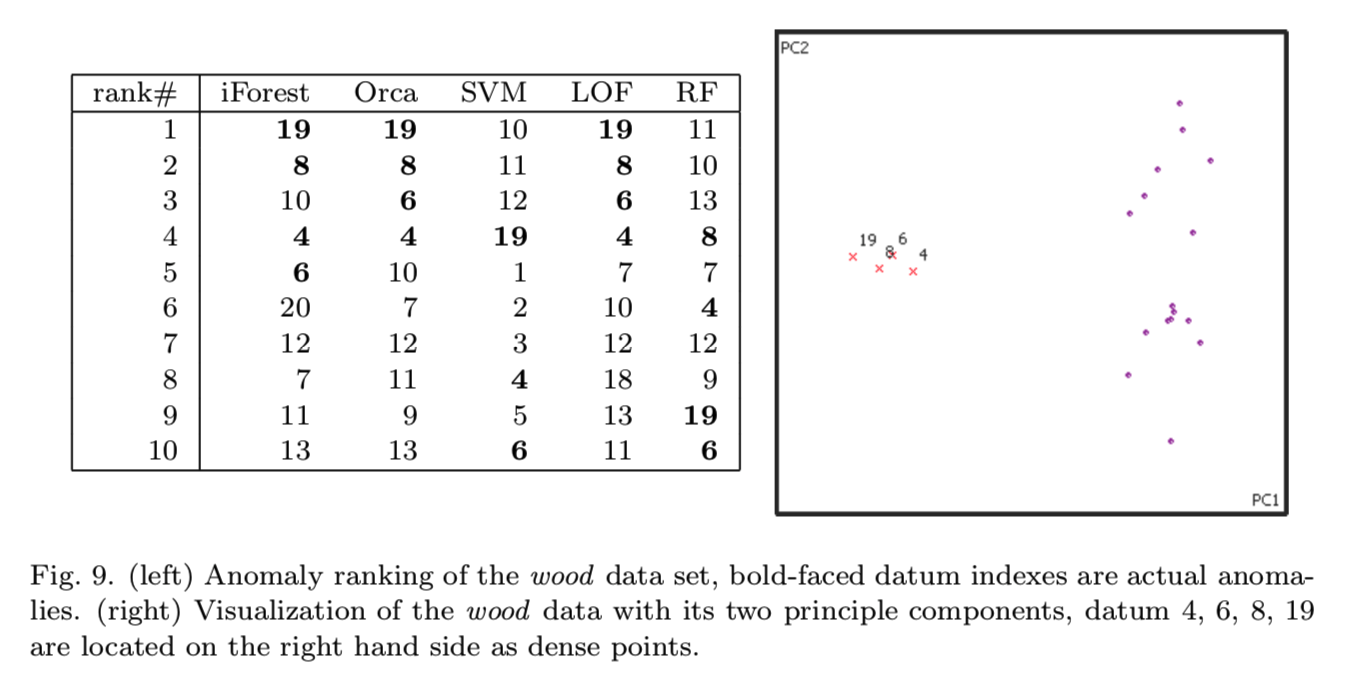
总的来说,iForest是唯一一个在这两个统计数据集中表现同样出色的异常检测器。
Performance Evaluation.第二个实验的目的是比较iForest与ORCA、LOF、SVM、RF的AUC和处理时间。
表IV报告了AUC分数和所有方法的实际运行时间。从表中可以看出,iForest在AUC和处理时间上都优于其他所有方法。特别是,对于大于1000个点的数据集,iForest是最快和最准确的。唯一的例外是表IV(a)所示的ForestCover数据集,其中SVM的AUC略好于iForest(AUC相差0.03)。
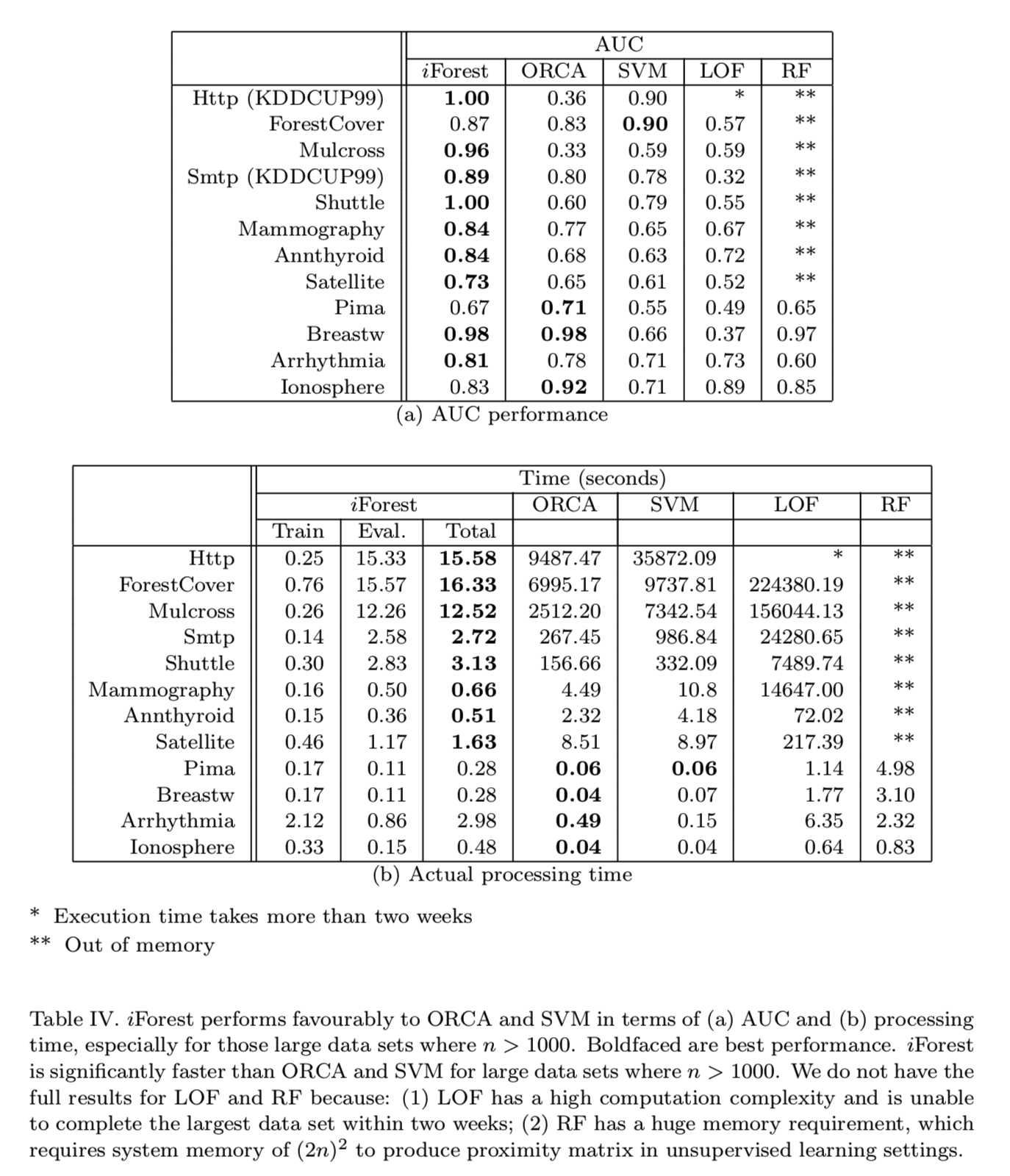
注意,iForest、ORCA、SVM和LOF之间的执行时间差异很大,尤其是在大数据集上;这是因为iForest不需要像ORCA和LOF那样计算成对距离,也不需要像SVM那样进行核优化。注意,LOF的运行时间较长,RF的内存要求较高;它们无法在大型数据集上运行。
在AUC方面,iForest在12个数据集中有9个对ORCA比较有利,SVM在12个数据集中有11个,LOF在8个数据集中有7个,RF在4个数据集中有4个。在处理时间上,iForest在大于1000点的数据集上优于ORCA和SVM,在所有数据集上iForest都优于LOF和RF。
iForest的性能是稳定在一个广泛的t值(即树的数量)间。使用两个有着最大的维数的数据集,图10显示了AUC收敛在一个小t上。完整的结果可在附录b 查看。因为增加t也会增加处理时间,AUC的早期收敛表明如果将t调到一个数据集,iForest的执行时间可以进一步降低:

对于Http和Mulcross数据集,由于异常集群的大小很大,而且与正常实例相比异常集群具有相同或更高的密度(即遮挡效应),在这些数据集上ORCA报告的结果比随机猜测的结果差。我们还使用了更高的k值(其中k = 150)对这些数据集进行了ORCA实验,但是检测性能相似。这突显出一个在ORCA数据集中有问题的假设和其他类似的基于k-nn的方法:他们只能检测到大小小于k的低密度异常集群数据的。增加k可能会解决这个问题,但由于处理时间的增加,这是一个不实际的高容量设置,需要找到一个合适的k。
5.3 Breakdown Analysis with data-size-increasing Anomaly Clusters (Masking Effect)
在本小节中,我们将结合iForest通过设置不同的评估高度限制来改变检测行为的能力来研究其崩溃特性。为了便于比较,我们还研究了本节开始介绍的四种异常探测器的崩溃特性。
利用Mulcross数据生成器生成4096个带有不同污染(contamination)程度的异常和不同异常聚类数量的正常实例,检验了所有检测器的检测精度(AUC)。AUC通常随着污染水平的增加而下降——AUC下降的速度表明异常探测器在这种情况下崩溃的速度有多快。污染水平在a = 0.02和a = 0.5之间。
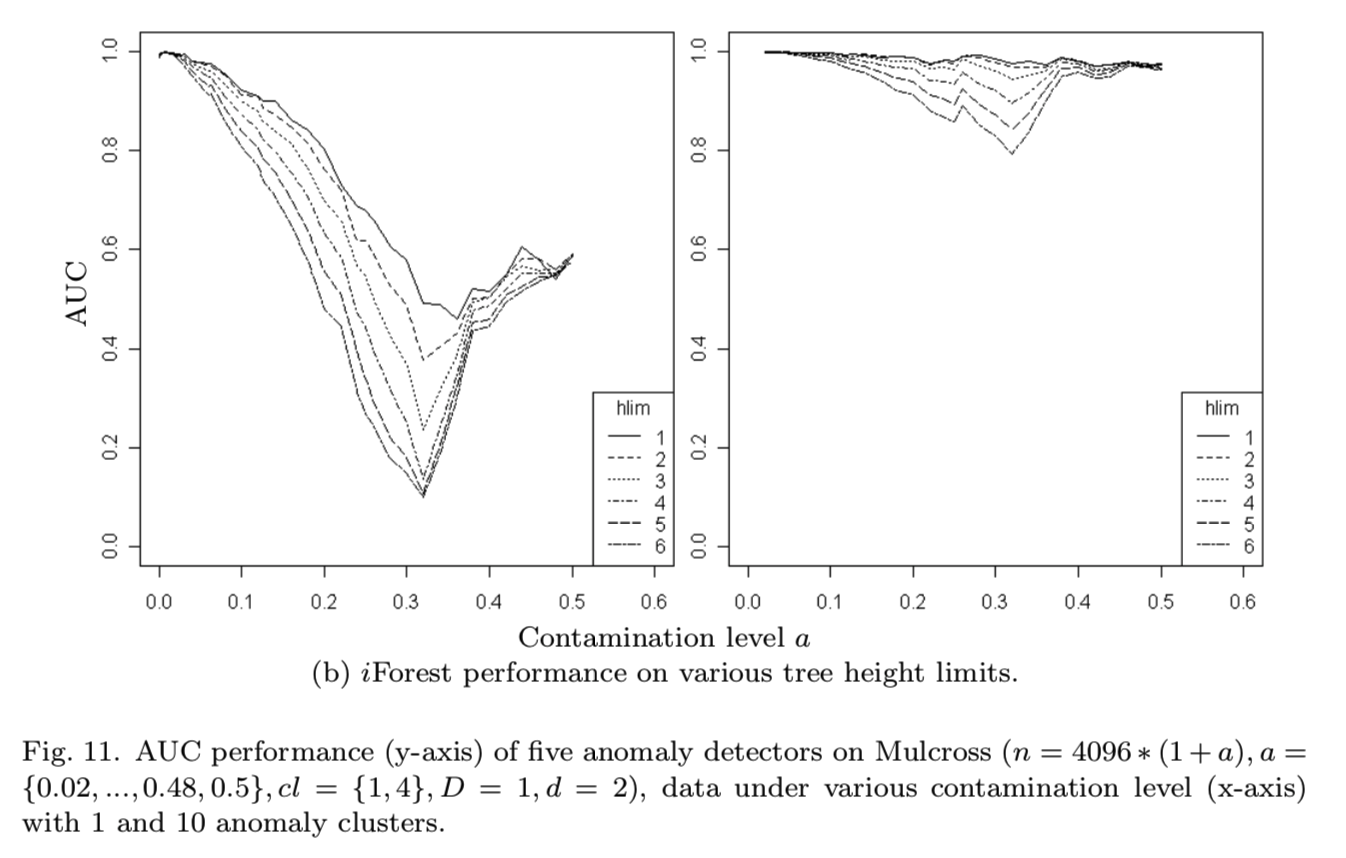
在图11(a)中,所有其他四个异常检测器在整个污染范围内的检测性能都明显低于iForest,尽管随着污染水平的增加,有些检测器的检测性能要优于其他检测器。密集异常集群对其他异常探测器的误导作用大于iforest,其中大部分在污染水平达到a = 0.1之前就崩溃了,检测性能很差;iForest更加健壮,随着污染水平的增加,它的崩溃更加缓慢。注意,有十个异常集群的问题要比只有一个异常集群的问题容易。这是因为相同数量的异常现在被分成十个簇,而不是集中在同一污染水平的一个集群上。iForest几乎保持了对整个污染范围的检测性能。但是,这对其他四个探测器的影响很小,异常集群的高体积和高密度仍然是一个难题。
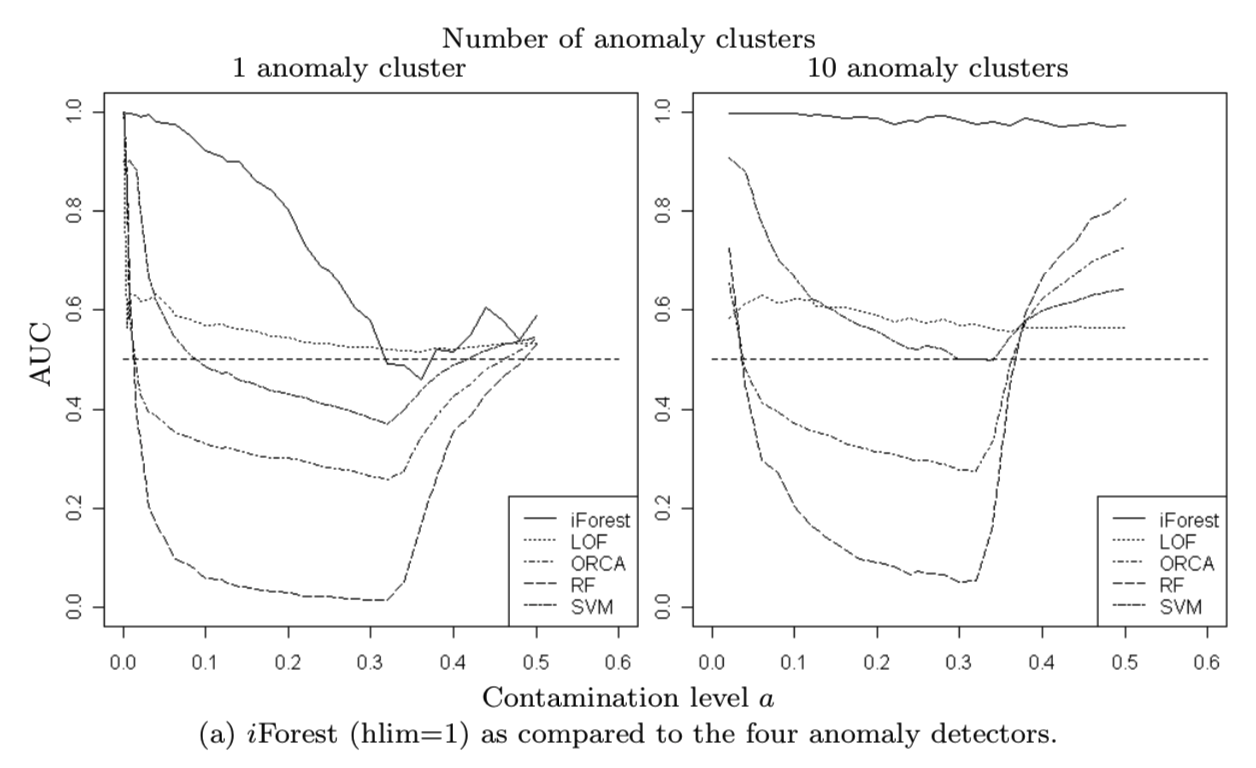
对于iForest,在图11(b)中,我们发现设置较低的评估高度限制对于处理密集的异常集群是有效的。iForest使用hlim = 1获得最佳性能。这是因为iForest使用最粗粒度来检测聚集异常。
5.4 Breakdown Analysis with Local Anomalies (Swamping Effect)
当异常与正常情况太接近时,由于异常的接近性,异常检测器就会崩溃。为了检验不同探测器对局部异常的鲁棒性,我们在两个不同密度的正常集群的背景下,生成离正常集群不同距离的异常。
我们使用距离因子= l/r,其中l为异常集群与正常集群中心之间的距离,r为正常集群的半径。当距离因子为1时,异常集群正好位于密度较大的正常集群的边缘。在本次评估中,LOF和ORCA取k = 15,使得k大于最大异常集群的大小。随机森林和支持向量机在此分析中表现不佳。为了清晰起见,本分析只显示了前三个检测器。
如图12(a)所示,当异常分散时,iForest的性能与LOF相似,其次是ORCA。当异常聚集在一起时,如图12(c)和(d)所示,iForest的性能明显优于LOF和ORCA。图12(b)和(d)显示了距离因子= 1.5的两种场景。iForest在集群异常中的突出表现归功于隔离的使用,它涵盖了整个数据集的上下文以及局部的上下文。当聚类异常接近正常聚类时,很难检测到异常,比如当它们与邻居相距不远,而且它们的相对密度与其他地点相似时。然而,这些聚集异常在整个数据集的上下文中仍然是可区分的,这就是为什么iForest能够很好地检测聚集异常:
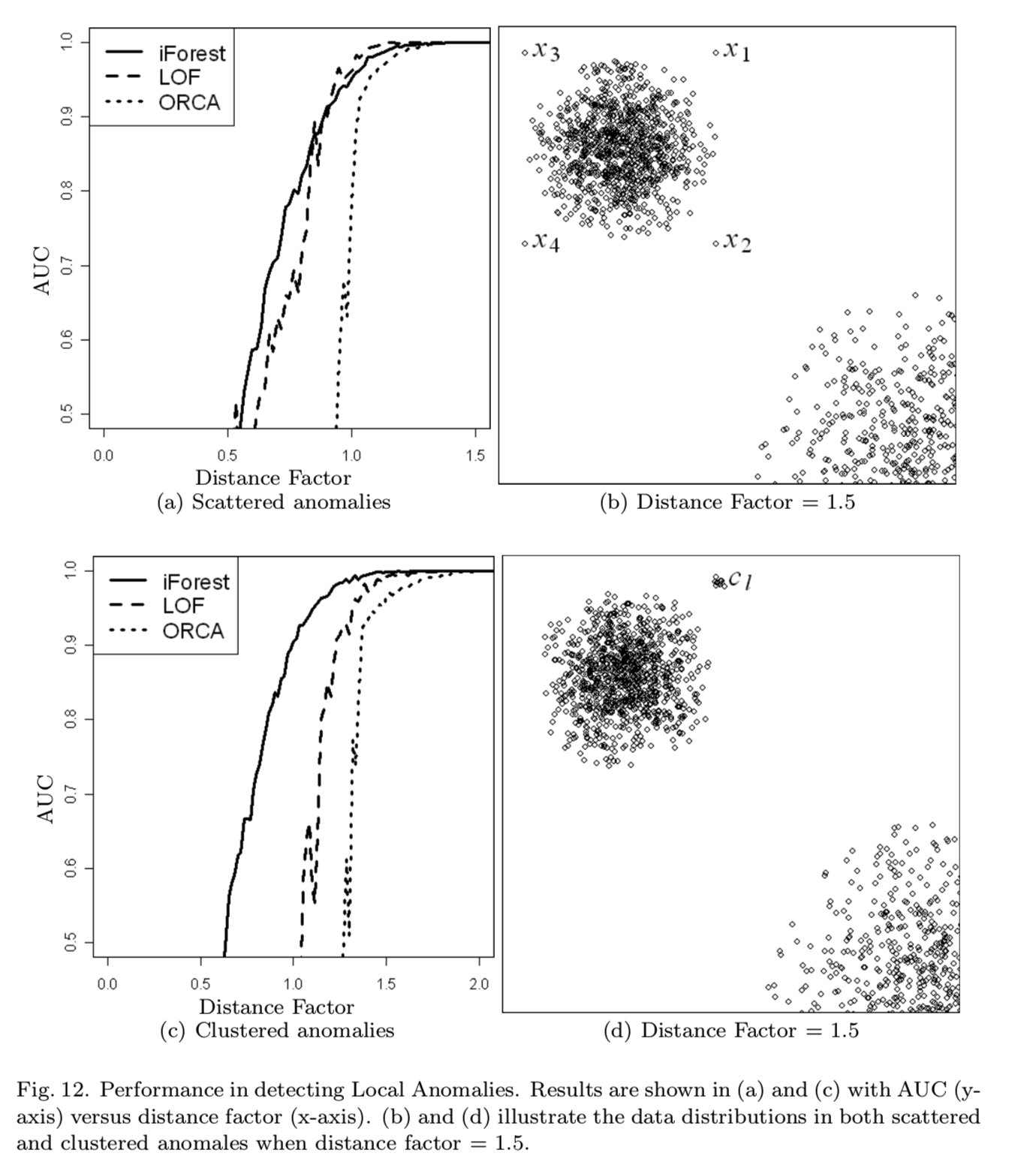
5.5 Analysis on the effect of subsampling
下面的实验根据内存需求和训练时间调查iForest的效率,子采样大小ψ相关。此外,我们还研究了在有限的数据供应下,探测器的性能如何。在这个实验中我们在范围ψ= 2,4,8,16,……,65536中调整子采样大小。
两个例子的研究结果如图13所示,我们观察到的iForest的AUC很快收敛在一个小ψ上。在ψ= 128时,Http的AUC接近最优;当ψ= 512时则是ForestCover,他们只有一小部分原始数据(Http为0.00045和ForestCover为0.0018),这使得iForest在使用小ψ时更高效。对于较大的ψ, AUC的变化很小:分别为±0.0014和±0.023。还要注意,当ψ从4增加到8192时处理时间增加非常缓慢。iForest在这个范围内保持了临近最优的检测性能。结果表明,该算法的检测性能主要来自于基于树的算法,而非子采样。ψ的增加在ψ> 64之后对Mulcross生成的数据有不利影响。这是由于密性异常集群的遮挡效应导致的。如4.4节所述,遮挡效应可以通过减少iForest中的子采样来解决。简而言之,高检测性能是iForest的特点和使用一个小ψ将导致较低的处理时间,以及进一步提高ψ是不必要的。所有数据集的完整结果见附录C。
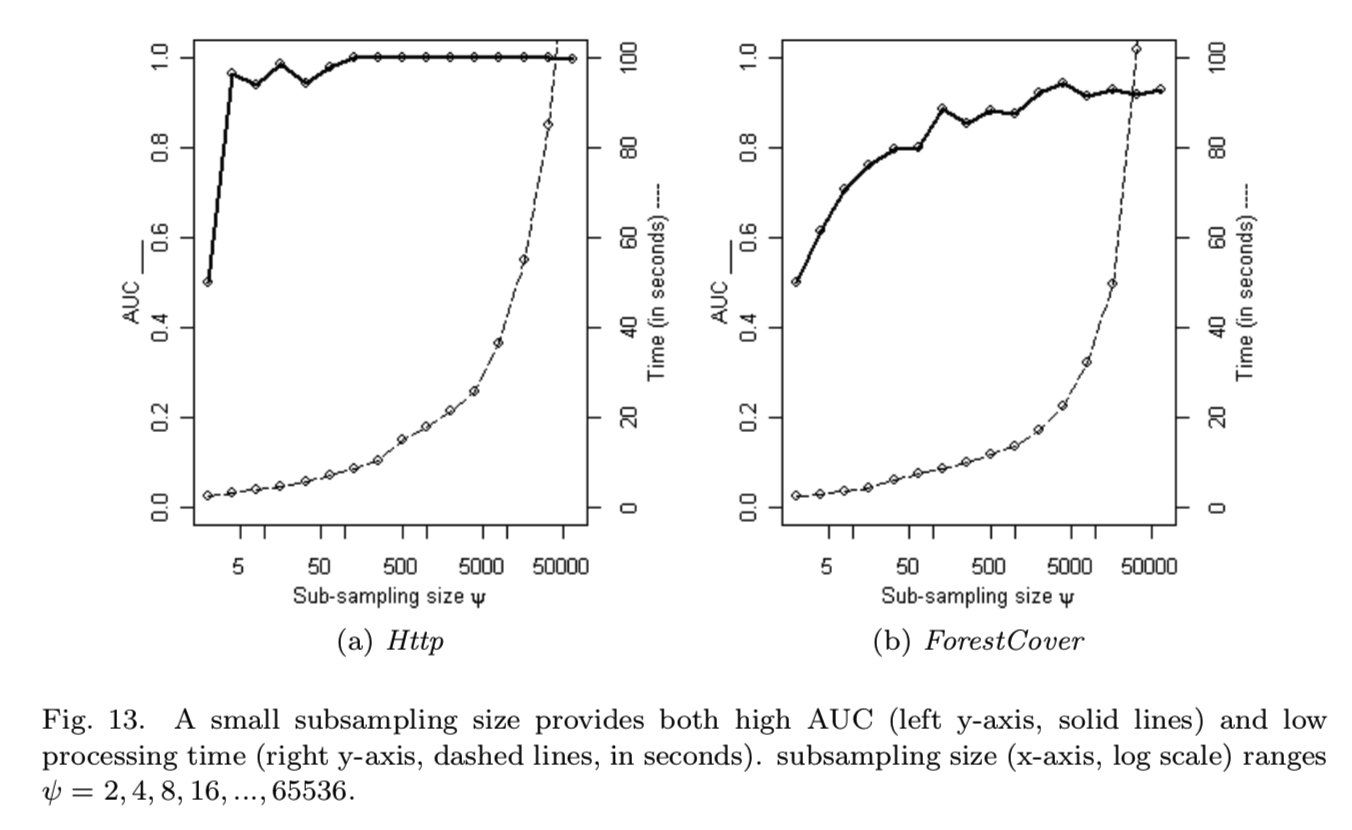
使用较小的子样本大小意味着可以轻松地以最小的内存占用来托管在线异常检测系统。使用ψ= 256,节点的最大数量是511。设节点的内存需求为b字节,t为树的个数。因此,检测异常的工作模型估计小于511tb字节,这在现代计算设备中是微不足道的。需要注意的是,使用固定数量的树和子采样大小,内存需求是恒定的。
至于训练时间,当我们在不同大小的Mulcross生成的数据中使用一个常数ψ= 256,iForest的训练时间在数据大小双倍增长时仅增长不到一半的大小,如表V所示:
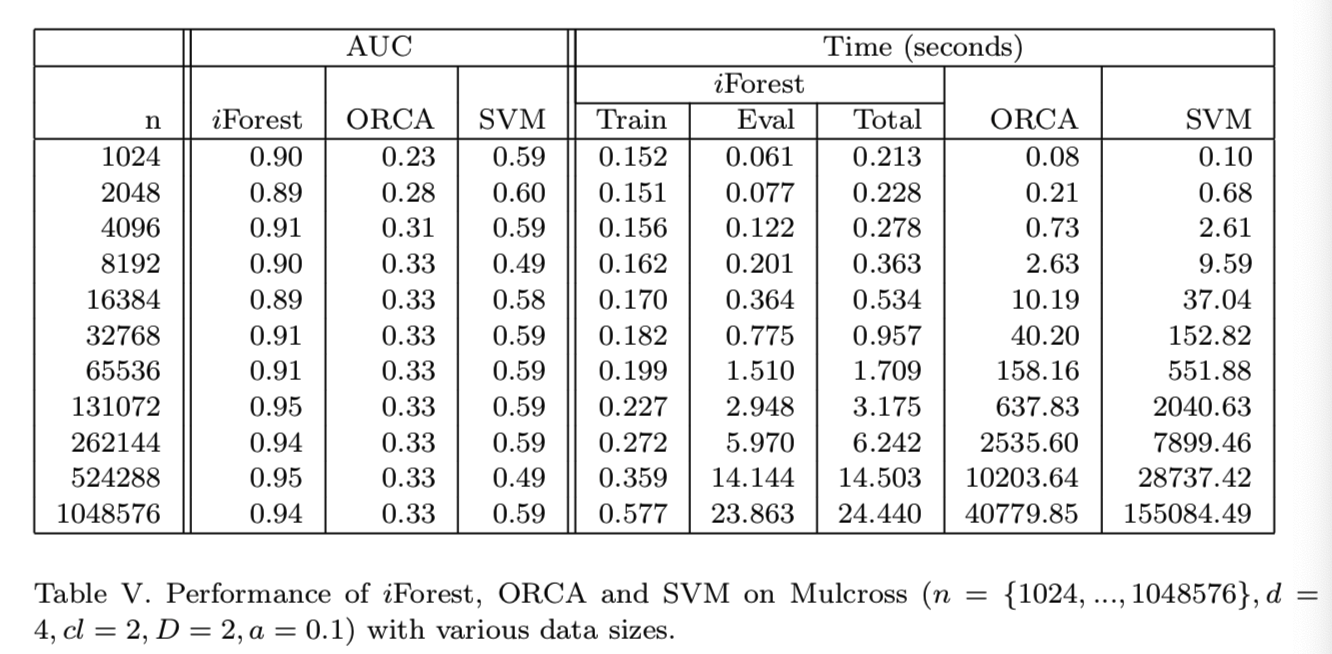
不考虑在加载训练数据到内存的操作和子采样过程,时间,构造t = 100棵树的时间是恒定的,大约0.04秒。只有当数据量非常大时,iForest的总处理时间才会以与数据量相同的速度增长;否则它就是次线性的。相比之下,ORCA和SVM的执行时间在数据翻番时都是数据大小的4倍左右。
当数据量较大时有很大的不同,如100万个数据点时,iForest从ORCA中提取的数据量不足ORCA的1 / 1500,从SVM中提取的数据量不足SVM的1 / 6000;而且检测精度也提高了很多。注意,使用较小的数据量并不能提高ORCA和SVM的检测结果。使用常数ψ和t时,构建iForest的运行时间和内存需求基本上是恒定的,无论训练数据的大小是多少。
此外,我们还根据AUC和处理时间研究了子采样在不同异常检测器的效果。每个实例的邻域从一个子样本到另一个子样本都发生了显著的变化;这可能会影响基于k近邻(k-nn)算法的性能。随着子样本中数据大小的减小,我们可以预期处理时间会减少。在下面的段落中,我们将演示使用两个数据集进行子采样的效果。
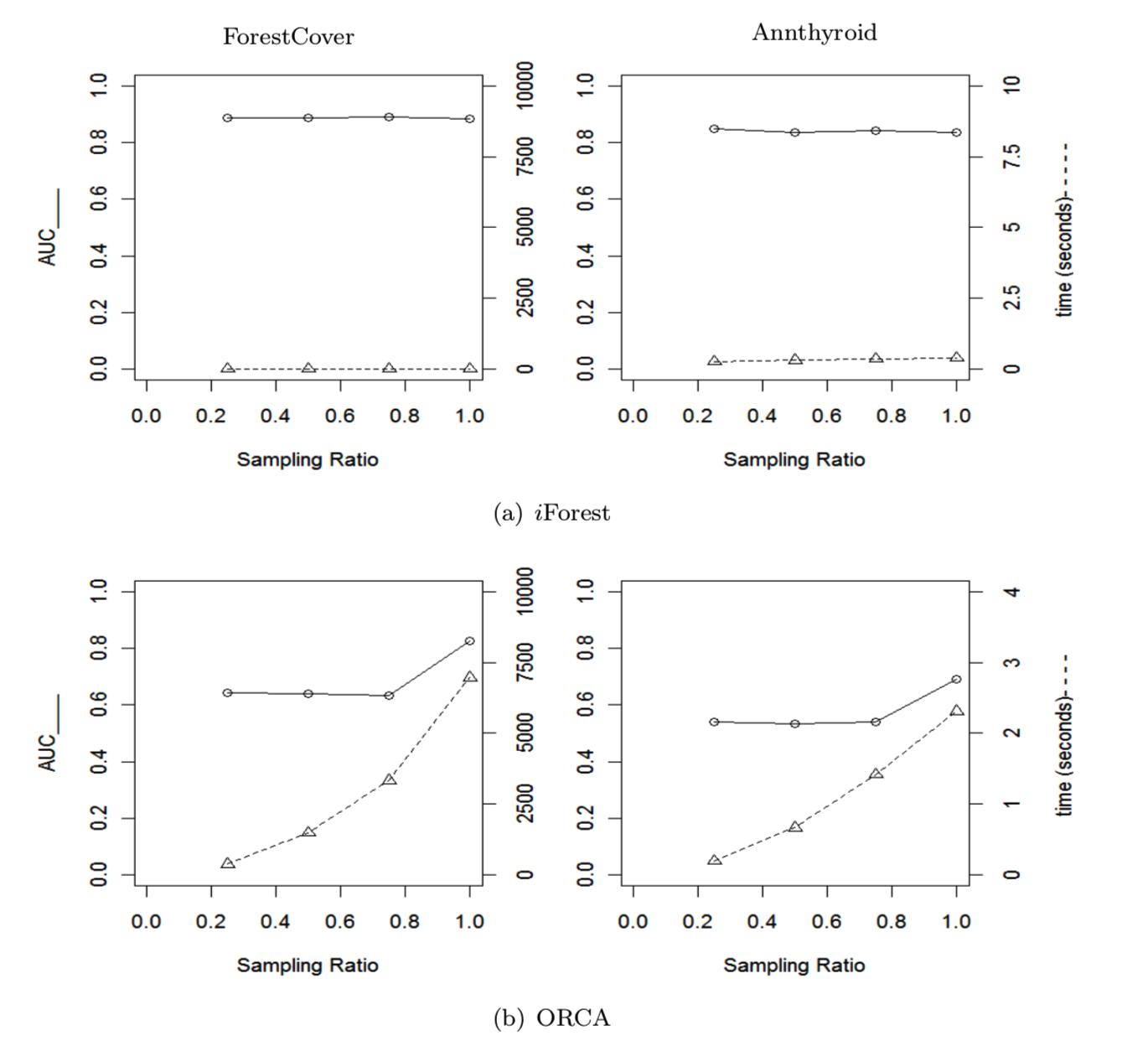
在图14中,三个检测器(a) iForest、(b) ORCA和(c) SVM)在原始数据集不同子采样大小下的性能分别以四种采样比(0.25、0.5、0.75和1.0)展示。我们观察到iForest和SVM在不同比例下的测试性能是稳定的(即上面那条线是直的)。然而,当采样率从1降低到0.75时,ORCA的检测性能会下降。ORCA中显示的检测性能类似于分类模型中常见的学习曲线,训练数据的减少通常会导致分类性能下降。与[Wu and Jermaine 2006]展示相同。由于SVM为正常点构造了一个边界,因此能够构造一个小样本的正常点边界;因此,SVM在采样率为0.25时达到了最佳的检测性能。然而,它的最佳表现并不是具有竞争性的,就像在Annthyroid数据中。
在处理时间方面(即下面那条线),ORCA和SVM的处理时间随着子采样大小的增加呈超线性增长,而iForest在ForestCover数据集上呈线性增长,在Annthyroid数据呈亚线性增长。上述结果表明,iForest适合于大数据集,因为它在处理时间上有线性或次线性的增长,并且在不同数据大小下具有稳定的检测性能。注意,iForest的时间复杂度是(对于训练和评估)是O (tψ(ψ+ n))。对于大型的数据集,其中n≫ψ,时间复杂度由n决定。

5.6 High Dimensional Data
异常检测的一个重要挑战是处理高维数据。对于基于距离或基于密度的方法,每个点在高维空间中都是同样稀疏的,呈现距离是无用的度量(注意,许多基于密度的方法使用距离来估计密度)。没有任何帮助,iForest也遭受同样的“维度诅咒”。但是,使用一个简单的属性选择器,我们将看到是否可以改进iForest处理高维数据的能力。
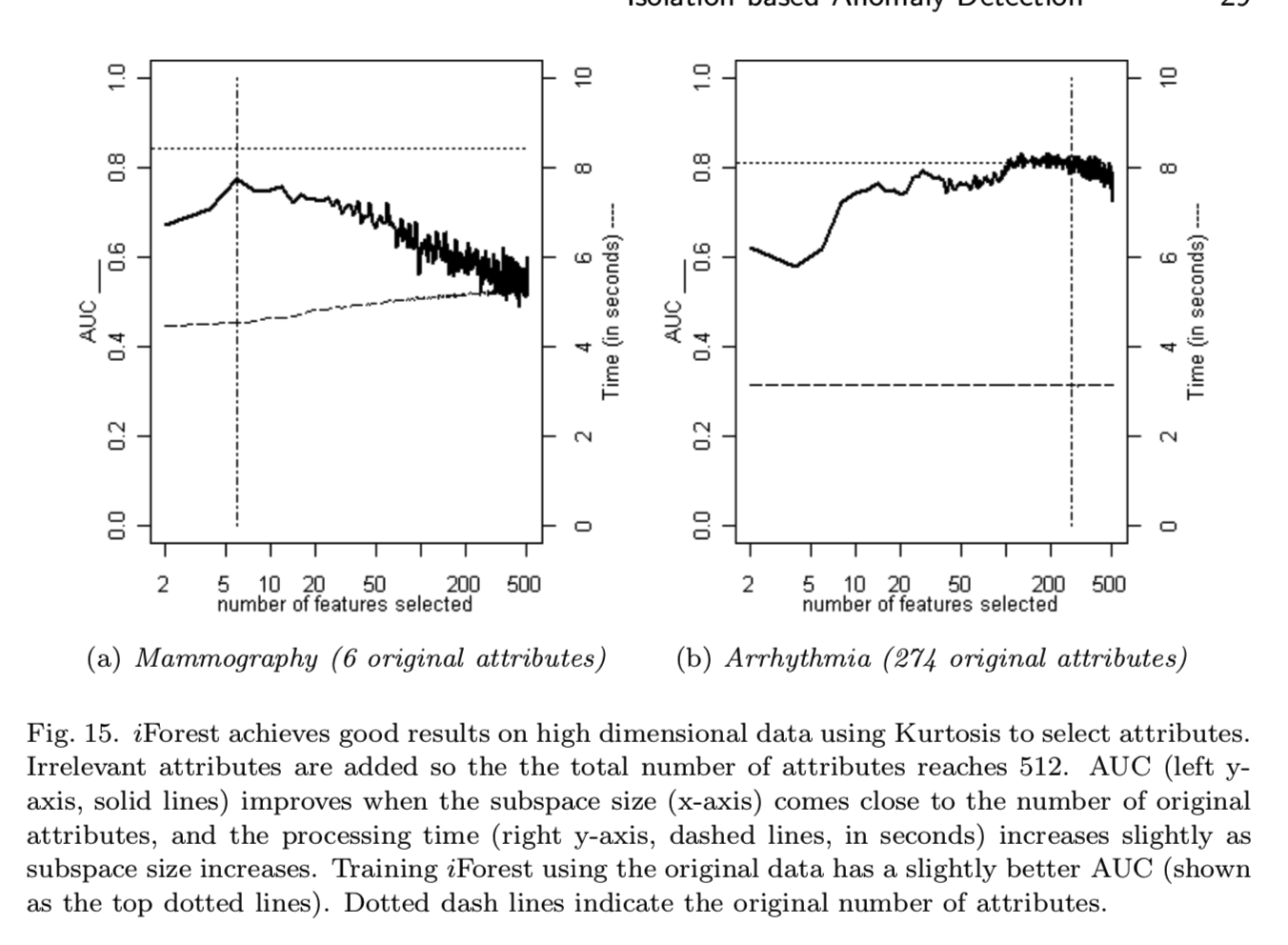
在本实验中,我们研究了一个高维数据的特殊情况,其中数据集具有大量不相关的属性。结果表明,iForest在处理时间上具有明显的优势。我们使用表III中介绍的前13个数据集模拟这些高维数据集。对于每个数据集,都添加值在0到1之间的均匀分布随机属性。因此,每个数据集中共有512个属性。我们使用一个简单的统计测试,Kurtosis[Joanes and Gill 1998],在构建每个iTree之前,从子采样中选择一个属性子空间。Kurtosis度量的是单变量分布的“峰度”。Kurtosis对异常的存在很敏感,是一种很好的异常检测属性选择器。当Kurtosis为每个属性提供了一个排序后,根据这个排序选择一个子空间的属性来构造每棵树。结果表明,当子空间大小接近原始属性个数时,检测性能得到了提高。我们还可以从其他属性选择器中进行选择,例如,Grubb的测试。然而,在本节中,我们只关注展示iForest在降低异常检测任务的维数方面使用属性选择器的能力。
如图15所示,a)在子空间大小的整个范围内,iForest在Mammography和Arrhythmia数据中的处理时间均小于10秒;b)当子空间大小等于原始属性个数时,AUC达到峰值。完整的结果见附录D。
当在这两个高维数据集上使用ORCA时,它报告AUC接近0.5,处理时间超过100秒。这表明这些高维数据集是具有挑战性的,然而,iForest能够通过一个简单的Kurtosis测试在小的子采样中而不是整个数据集上提高检测的性能。很可能有其他方法可以应用类似的属性约简技术来在高维数据提高检测精度,但是他们需要对整个数据集进行测试。iForest的另一个优点是即使在高维数据中处理时间也很短。
5.7 Training Using Normal Instances Only
“当训练集只包含正常实例时,iForest是否能工作?”为了回答这个问题,我们从训练样本中去除异常,并用异常和正常样本来评估训练后的模型。我们在表VI中报告了平均AUC。结果表明,异常的包含对检测性能没有影响,或者影响很小。
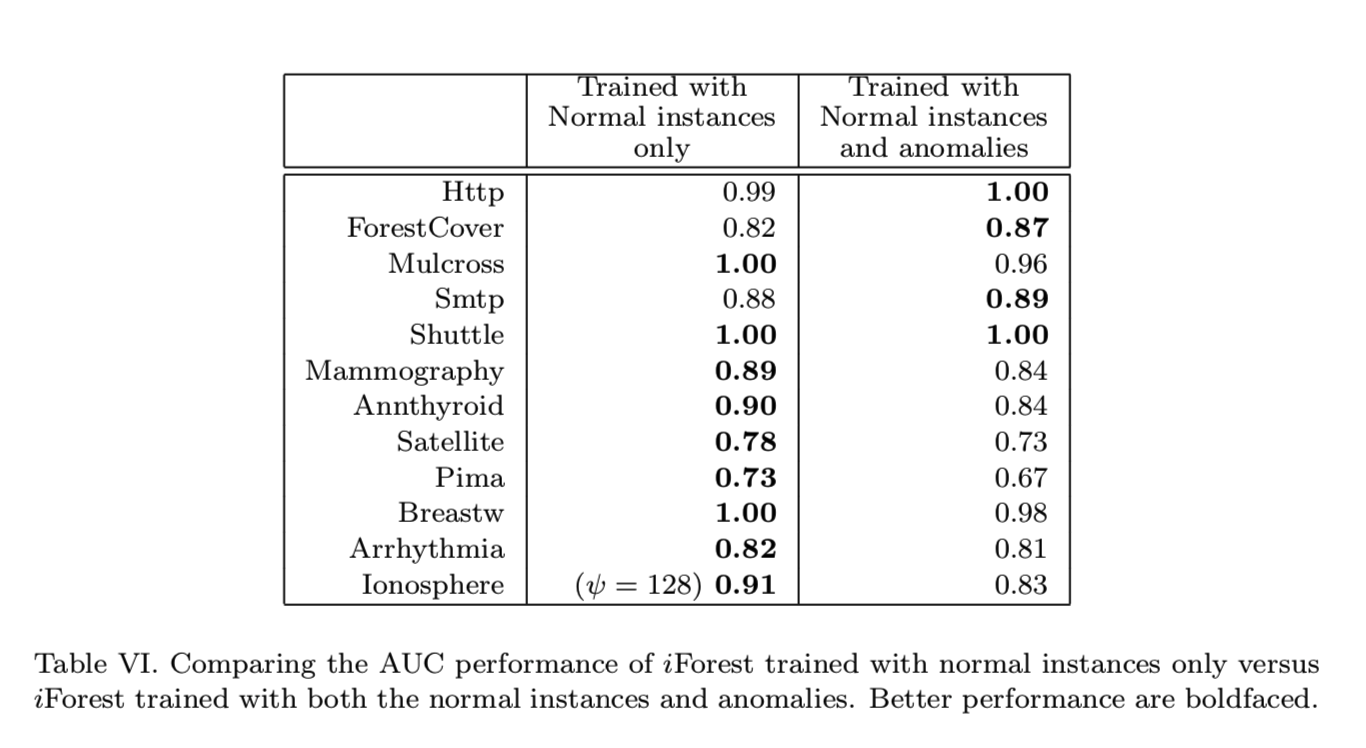
iForest在训练集中没有异常时仍然能够检测异常的原因是iForest描述了如附录A中所示的数据分布,其中高路径长度值对应于数据点的存在。因此,异常的存在与iForest的检测性能无关——在使用iForest时无需担心这一点。
8. CONCLUSIONS
本文提出了第一种隔离方法iForest,并在异常检测领域做出了三个关键贡献。首先,我们介绍了利用隔离作为一种比常用的基本距离和密度测量更高效和有效的异常检测手段。我们展示了隔离的概念,当在树结构中实现时,充分利用了异常的“少数和不同的”特性,与正常点相比,这些特性将异常隔离在离根节点更近的位置。这允许使用路径长度构造样本空间的概要。
其次,iForest是一种有着低线性时间复杂度、内存需求小的算法。无论数据集有多大,它都使用固定大小的小子采样和少量的树来构建一个性能良好的模型。它在训练过程中具有恒定的时间和空间复杂性。
第三,我们与四种最先进的异常探测器的经验对比表明,iForest在以下方面具有优势:
- 运行时间、检测精度和内存需求,特别是在大数据集,
- 与i)遮挡和淹没效应相关的鲁棒性,和ii)聚集异常能力
- 处理具有不相关属性的高维数据的能力。
我们还表明iForest能够:
- 在训练数据中有无异常情况下都能进行训练
- 提供不同粒度级别的检测结果,无需重新训练



