Example of DenseCRF with non-RGB data
本笔记本通过一个示例说明如何在非rgb数据上使用DenseCRFs。同时,它将解释基本概念并通过一个示例进行演示,因此即使您正在处理RGB数据,它也可能是有用的,不过也请查看PyDenseCRF's README !
在jupyter notebook上运行https://github.com/lucasb-eyer/pydensecrf/tree/master/examples/Non RGB Example.ipynb
Basic setup
先导入:
import pydensecrf.densecrf as dcrf
from pydensecrf.utils import unary_from_softmax, create_pairwise_bilateral
设置画图风格:
import numpy as np import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['image.interpolation'] = 'nearest' #设置插入风格 plt.rcParams['image.cmap'] = 'gray' #设置颜色风格
Unary Potential一元势
一元势由每个像素的类概率组成。这可以来自任何类型的模型,如随机森林或深度神经网络的softmax。
1)Create unary potential
补充:scipy.stats.multivariate_normal的使用
1.得到x,y的取值
from scipy.stats import multivariate_normal H, W, NLABELS = 400, 512, 2 # This creates a gaussian blob... a = np.mgrid[0:H, 0:W] #(2,400,512) #得到x,y的取值 a,a.shape
返回:
(array([[[ 0, 0, 0, ..., 0, 0, 0], [ 1, 1, 1, ..., 1, 1, 1], [ 2, 2, 2, ..., 2, 2, 2], ..., [397, 397, 397, ..., 397, 397, 397], [398, 398, 398, ..., 398, 398, 398], [399, 399, 399, ..., 399, 399, 399]], [[ 0, 1, 2, ..., 509, 510, 511], [ 0, 1, 2, ..., 509, 510, 511], [ 0, 1, 2, ..., 509, 510, 511], ..., [ 0, 1, 2, ..., 509, 510, 511], [ 0, 1, 2, ..., 509, 510, 511], [ 0, 1, 2, ..., 509, 510, 511]]]), (2, 400, 512))
2.得到点(x,y)的值
pos = np.stack(a, axis=2) #得到(x,y)点的值 pos,pos.shape
返回:
(array([[[ 0, 0], [ 0, 1], [ 0, 2], ..., [ 0, 509], [ 0, 510], [ 0, 511]], [[ 1, 0], [ 1, 1], [ 1, 2], ..., [ 1, 509], [ 1, 510], [ 1, 511]], [[ 2, 0], [ 2, 1], [ 2, 2], ..., [ 2, 509], [ 2, 510], [ 2, 511]], ..., [[397, 0], [397, 1], [397, 2], ..., [397, 509], [397, 510], [397, 511]], [[398, 0], [398, 1], [398, 2], ..., [398, 509], [398, 510], [398, 511]], [[399, 0], [399, 1], [399, 2], ..., [399, 509], [399, 510], [399, 511]]]), (400, 512, 2))
3.得到概率值:
#mean=[200, 256], cov=12800,12800的单位乘作为协方差矩阵 rv = multivariate_normal([H//2, W//2], (H//4)*(W//4)) probs = rv.pdf(pos) probs,probs.shape
返回:
(array([[2.01479637e-07, 2.05541767e-07, 2.09669414e-07, ..., 2.13863243e-07, 2.09669414e-07, 2.05541767e-07], [2.04644486e-07, 2.08770423e-07, 2.12962908e-07, ..., 2.17222613e-07, 2.12962908e-07, 2.08770423e-07], [2.07842810e-07, 2.12033230e-07, 2.16291237e-07, ..., 2.20617517e-07, 2.16291237e-07, 2.12033230e-07], ..., [2.11074628e-07, 2.15330207e-07, 2.19654423e-07, ..., 2.24047973e-07, 2.19654423e-07, 2.15330207e-07], [2.07842810e-07, 2.12033230e-07, 2.16291237e-07, ..., 2.20617517e-07, 2.16291237e-07, 2.12033230e-07], [2.04644486e-07, 2.08770423e-07, 2.12962908e-07, ..., 2.17222613e-07, 2.12962908e-07, 2.08770423e-07]]), (400, 512))
4.将概率值进行处理集中到[0.4,0.6]区间中
先将值集中到[0,1]区间中
# ...which we project into the range [0.4, 0.6] probs = (probs-probs.min()) / (probs.max()-probs.min()) probs, probs.shape
返回:
(array([[0. , 0.00033208, 0.00066951, ..., 0.00101235, 0.00066951, 0.00033208], [0.00025872, 0.00059602, 0.00093875, ..., 0.00128698, 0.00093875, 0.00059602], [0.00052019, 0.00086275, 0.00121084, ..., 0.00156451, 0.00121084, 0.00086275], ..., [0.00078439, 0.00113228, 0.00148578, ..., 0.00184495, 0.00148578, 0.00113228], [0.00052019, 0.00086275, 0.00121084, ..., 0.00156451, 0.00121084, 0.00086275], [0.00025872, 0.00059602, 0.00093875, ..., 0.00128698, 0.00093875, 0.00059602]]), (400, 512))
再将其集中到[0.4,0.6]区间中,0.5 + 0.2 * (probs-0.5)等价于0.4+0.2*probs,而此时的probs为[0,1]区间中的值:
probs = 0.5 + 0.2 * (probs-0.5) #此时probs.shape为(400, 512) probs, probs.shape #将最终的概率结果的值集中在[0.4, 0.6]区间中
返回:
(array([[0.4 , 0.40006642, 0.4001339 , ..., 0.40020247, 0.4001339 , 0.40006642], [0.40005174, 0.4001192 , 0.40018775, ..., 0.4002574 , 0.40018775, 0.4001192 ], [0.40010404, 0.40017255, 0.40024217, ..., 0.4003129 , 0.40024217, 0.40017255], ..., [0.40015688, 0.40022646, 0.40029716, ..., 0.40036899, 0.40029716, 0.40022646], [0.40010404, 0.40017255, 0.40024217, ..., 0.4003129 , 0.40024217, 0.40017255], [0.40005174, 0.4001192 , 0.40018775, ..., 0.4002574 , 0.40018775, 0.4001192 ]]), (400, 512))
5.一份数据已经准备好了,要复制生成一个效果相反的数据:
# 第一个维度需要等于类的数量,这里设置两个类,为2 # 让我们有一个"foreground"和一个"background"类 #因此,复制高斯blob,但倒置它去创建与“background”类的概率是相反的“foreground”类。 #np.tile(a,(m,n)):即是把a数组里面的元素复制n次放进一个数组c中,然后再把数组c复制m次放进一个数组b中 #np.tile(a,(2,3)) #将a数组重复3次形成2行的数组 #np.newaxis为多维数组增加一个轴 #probs[np.newaxis,:,:].shape为(1, 400, 512) probs = np.tile(probs[np.newaxis,:,:],(2,1,1))#此时probs.shape为(2, 400, 512) probs[1,:,:] = 1 - probs[0,:,:] #得到相反的值
probs,probs.shape
返回:
(array([[[0.4 , 0.40006642, 0.4001339 , ..., 0.40020247, 0.4001339 , 0.40006642], [0.40005174, 0.4001192 , 0.40018775, ..., 0.4002574 , 0.40018775, 0.4001192 ], [0.40010404, 0.40017255, 0.40024217, ..., 0.4003129 , 0.40024217, 0.40017255], ..., [0.40015688, 0.40022646, 0.40029716, ..., 0.40036899, 0.40029716, 0.40022646], [0.40010404, 0.40017255, 0.40024217, ..., 0.4003129 , 0.40024217, 0.40017255], [0.40005174, 0.4001192 , 0.40018775, ..., 0.4002574 , 0.40018775, 0.4001192 ]], [[0.6 , 0.59993358, 0.5998661 , ..., 0.59979753, 0.5998661 , 0.59993358], [0.59994826, 0.5998808 , 0.59981225, ..., 0.5997426 , 0.59981225, 0.5998808 ], [0.59989596, 0.59982745, 0.59975783, ..., 0.5996871 , 0.59975783, 0.59982745], ..., [0.59984312, 0.59977354, 0.59970284, ..., 0.59963101, 0.59970284, 0.59977354], [0.59989596, 0.59982745, 0.59975783, ..., 0.5996871 , 0.59975783, 0.59982745], [0.59994826, 0.5998808 , 0.59981225, ..., 0.5997426 , 0.59981225, 0.5998808 ]]]), (2, 400, 512))
6.最终的代码为:
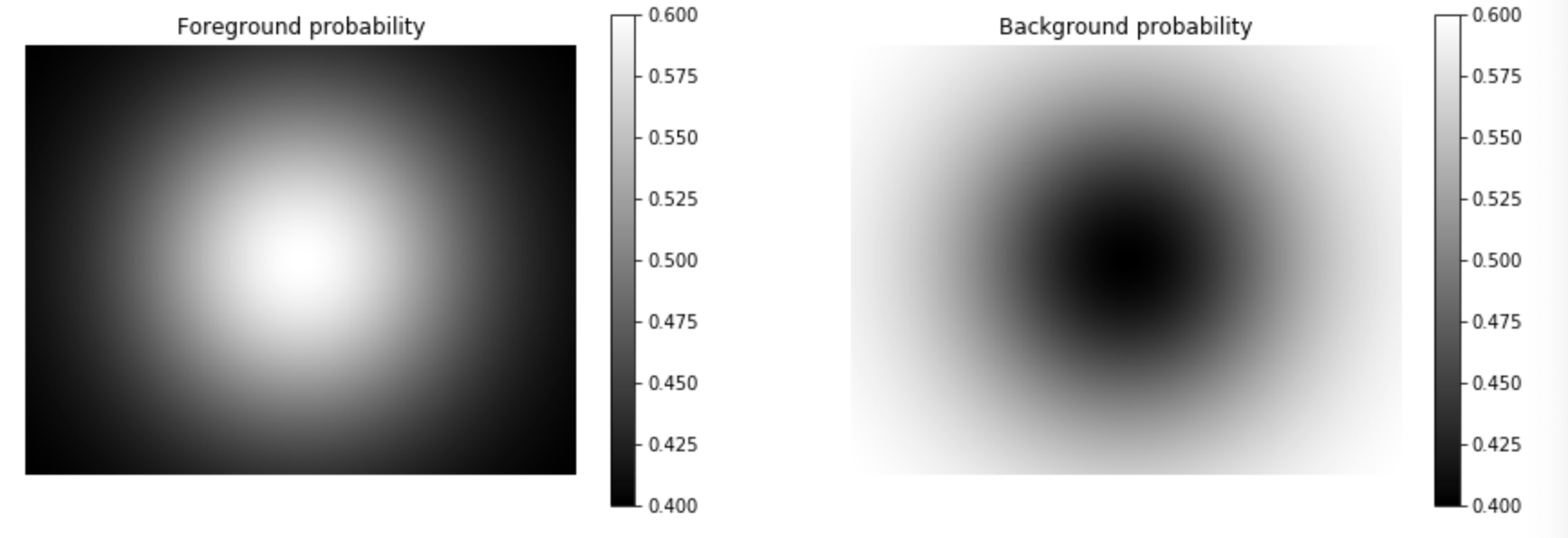
from scipy.stats import multivariate_normal H, W, NLABELS = 400, 512, 2 # This creates a gaussian blob... pos = np.stack(np.mgrid[0:H, 0:W], axis=2) rv = multivariate_normal([H//2, W//2], (H//4)*(W//4)) probs = rv.pdf(pos) # ...which we project into the range [0.4, 0.6] probs = (probs-probs.min()) / (probs.max()-probs.min()) probs = 0.5 + 0.2 * (probs-0.5) #此时probs.shape为(400, 512) # 第一个维度需要等于类的数量 # 让我们有一个"foreground"和一个"background"类 #因此,复制高斯blob,但倒置它去创建与“background”类的概率是相反的“foreground”类。 #np.tile(a,(m,n)):即是把a数组里面的元素复制n次放进一个数组c中,然后再把数组c复制m次放进一个数组b中 #np.tile(a,(2,3)) #将a数组重复3次形成2行的数组 #np.newaxis为多维数组增加一个轴 #probs[np.newaxis,:,:].shape为(1, 400, 512) probs = np.tile(probs[np.newaxis,:,:],(2,1,1))#此时probs.shape为(2, 400, 512) probs[1,:,:] = 1 - probs[0,:,:] #得到相反的值 # Let's have a look: plt.figure(figsize=(15,5)) plt.subplot(1,2,1); plt.imshow(probs[0,:,:]); plt.title('Foreground probability'); plt.axis('off'); plt.colorbar(); plt.subplot(1,2,2); plt.imshow(probs[1,:,:]); plt.title('Background probability'); plt.axis('off'); plt.colorbar();
返回:
2)Run inference with unary potential 使用一元势运行推理
我们已经可以运行一个只有一元势的DenseCRF。这不是一个好主意,但我们可以做到:
1.unary_from_softmax函数的作用
将softmax类概率转换为一元势(每个节点的NLL)。
即我们之前先对图片使用训练好的网络预测得到最终经过softmax函数得到的分类结果,这里需要将这个结果转成一元势
参数
- sm: numpy.array ,第一个维度是类的softmax的输出,其他所有维度都是flattend。这意味着“sm.shape[0] == n_classes”。
- scale: float,softmax输出的确定性(默认为None),需要值在(0,1]。如果不为None,则softmax输出被缩放到从[0,scale]概率的范围。
- clip: float,将概率裁剪到的最小值。这是因为一元函数是概率的负对数,而log(0) = inf,所以我们需要把0概率裁剪成正的值。
在这里因为scale=None,clip=None,所以这个函数的作用其实只进行了下面的操作:
-np.log(sm).reshape([num_cls, -1]).astype(np.float32)
对值取负对数,并将结果变为(2, 204800)大小,进行了flatten操作,将图片压扁了:
# Inference without pair-wise terms #设置固定的一元势 from pydensecrf.utils import unary_from_softmax U = unary_from_softmax(probs) # note: num classes is first dim,类别在第一维 U,U.shape
返回:
(array([[0.91629076, 0.9161247 , 0.915956 , ..., 0.91564745, 0.9158215 , 0.9159928 ], [0.51082563, 0.5109363 , 0.5110488 , ..., 0.5112547 , 0.5111386 , 0.5110243 ]], dtype=float32), (2, 204800))
此时的值就是一元势了
d = dcrf.DenseCRF2D(W, H, NLABELS) d.setUnaryEnergy(U) # Run inference for 10 iterations,10次迭代 Q_unary = d.inference(10) # Q现在是近似后验,我们可以用argmax得到一个MAP估计值。 #np.argmax得到Q_unary列方向上的最大值的索引 map_soln_unary = np.argmax(Q_unary, axis=0)#此时形式为(204800,)
map_soln_unary,map_soln_unary.shape
返回:
(array([1, 1, 1, ..., 1, 1, 1]), (204800,))
# 不幸的是,DenseCRF把所有东西都压扁了,所以把它恢复到图片形式。 map_soln_unary = map_soln_unary.reshape((H,W)) #重新变为(400, 512)) map_soln_unary,map_soln_unary.shape
返回:
(array([[1, 1, 1, ..., 1, 1, 1], [1, 1, 1, ..., 1, 1, 1], [1, 1, 1, ..., 1, 1, 1], ..., [1, 1, 1, ..., 1, 1, 1], [1, 1, 1, ..., 1, 1, 1], [1, 1, 1, ..., 1, 1, 1]]), (400, 512))
总的代码为:
# Inference without pair-wise terms U = unary_from_softmax(probs) # note: num classes is first dim d = dcrf.DenseCRF2D(W, H, NLABELS) d.setUnaryEnergy(U) # Run inference for 10 iterations,10次迭代 Q_unary = d.inference(10) # Q现在是近似后验,我们可以用argmax得到一个MAP估计值。 #np.argmax得到Q_unary列方向上的最大值的索引 map_soln_unary = np.argmax(Q_unary, axis=0)#此时形式为(204800,) # 不幸的是,DenseCRF把所有东西都压扁了,所以把它恢复到图片形式。 map_soln_unary = map_soln_unary.reshape((H,W))#重新变为(400, 512)) # And let's have a look. plt.imshow(map_soln_unary); plt.axis('off'); plt.title('MAP Solution without pairwise terms');
返回:

因为设置了颜色为gray,实际结果为:

Pairwise terms二元
DenseCRFs的全部意义在于使用某种形式的内容来平滑预测。这是通过“成对”术语来实现的,“成对”术语编码元素之间的关系。
1)Add (non-RGB) pairwise term
例如,在图像处理中,一个流行的成对关系是“双边”(bilateral)关系,它大致表示颜色相似或位置相似的像素可能属于同一个类。
NCHAN=1 #通道为1,non-RGB #创造简单的双边图象。 #注意,我们将通道维度放在最后,但我们也可以将它作为第一个维度,只要将chdim参数进一步更改为0。 img = np.zeros((H,W,NCHAN), np.uint8) img[H//3:2*H//3,W//4:3*W//4,:] = 1 #使得[133:266,128:384,:]内的值为1,下面画为白色 plt.imshow(img[:,:,0]); plt.title('Bilateral image'); plt.axis('off'); plt.colorbar();
返回:

2.create_pairwise_bilateral函数的作用
创造成对双边势的Util函数。这适用于所有的图像尺寸。对于2D情况,与“densecrf2 . addpairwisebilateral”函数效果相同。
参数:
- sdims: list or tuple,每个维度的比例因子。这在DenseCRF2D.addPairwiseBilateral中称为“sxy”。
- schan: list or tuple,图像中每个通道的比例因子。这在DenseCRF2D.addPairwiseBilateral中称为“srgb”。
- img: numpy.array,输入的图像
- chdim: int, 可选。这指定了通道维度在图像中的位置。例如,' chdim=2 '用于大小为(240,300,3)的RGB图像,说明其通道3值放在维度2上(维度从0开始)。如果图像没有通道尺寸(例如只有一个通道),则使用' chdim=-1 '。
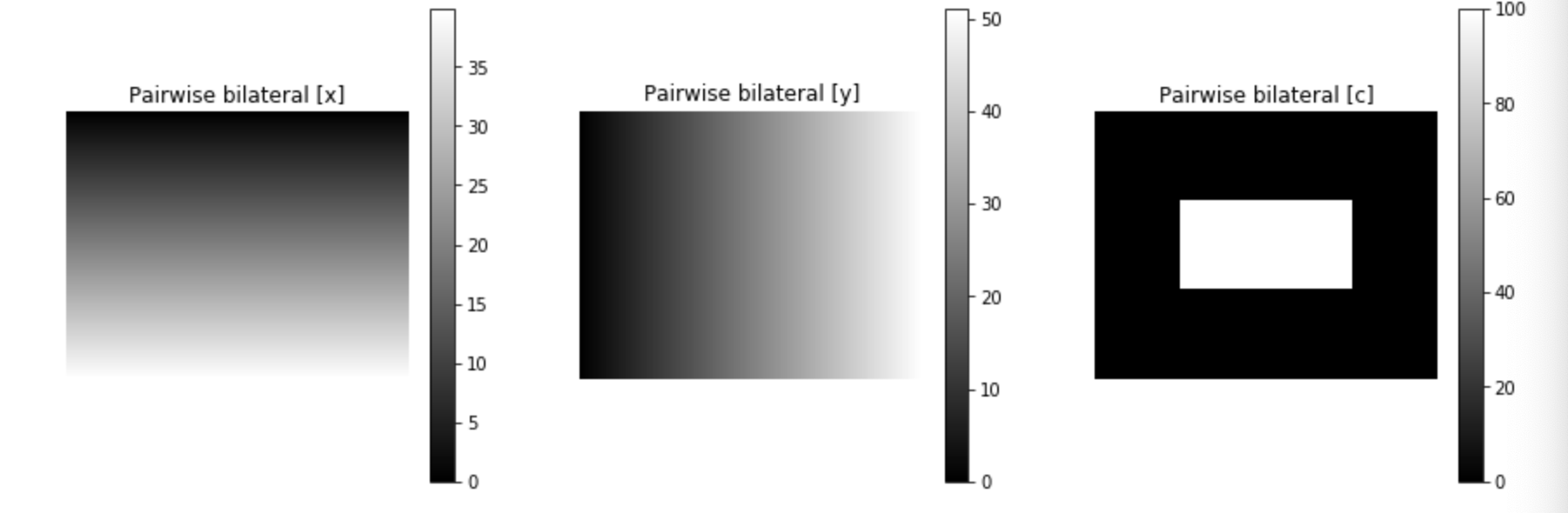
#从上图中创建成对的双边术语。 #这两个' s{dims,chan} '参数是模型超参数,分别定义了位置的强度和图像内容的双边参数。 #将通道为1的图变为了通道为3的图 pairwise_energy = create_pairwise_bilateral(sdims=(10,10), schan=(0.01,), img=img, chdim=2) #其shape为(3, 204800) #pairwise_energy现在包含的维度和DenseCRF的特性一样多,在本例中是3:(x,y,channel1) img_en = pairwise_energy.reshape((-1, H, W)) # Reshape just for plotting,为了画图 #下面将三个通道对应的图画出来 plt.figure(figsize=(15,5)) plt.subplot(1,3,1); plt.imshow(img_en[0]); plt.title('Pairwise bilateral [x]'); plt.axis('off'); plt.colorbar(); plt.subplot(1,3,2); plt.imshow(img_en[1]); plt.title('Pairwise bilateral [y]'); plt.axis('off'); plt.colorbar(); plt.subplot(1,3,3); plt.imshow(img_en[2]); plt.title('Pairwise bilateral [c]'); plt.axis('off'); plt.colorbar();
返回:
2)Run inference of complete DenseCRF
现在我们可以创建一个包含一元势和成对势的dense CRF ,并对其进行推理以得到最终结果。
d = dcrf.DenseCRF2D(W, H, NLABELS) d.setUnaryEnergy(U) #设置一元势 #添加二元势 d.addPairwiseEnergy(pairwise_energy, compat=10) # `compat` is the "strength" of this potential. #这一次,让我们自己分步骤进行推理,这样我们就可以查看中间解,并监视KL-divergence,它表明我们收敛得有多好。 #PyDenseCRF还要求我们跟踪计算所需的两个临时缓冲区,tmp1, tmp2。 Q, tmp1, tmp2 = d.startInference() for _ in range(5): #迭代5次后,查看结果 d.stepInference(Q, tmp1, tmp2) kl1 = d.klDivergence(Q) / (H*W) map_soln1 = np.argmax(Q, axis=0).reshape((H,W)) for _ in range(20): d.stepInference(Q, tmp1, tmp2) kl2 = d.klDivergence(Q) / (H*W) map_soln2 = np.argmax(Q, axis=0).reshape((H,W)) for _ in range(50): d.stepInference(Q, tmp1, tmp2) kl3 = d.klDivergence(Q) / (H*W) map_soln3 = np.argmax(Q, axis=0).reshape((H,W)) img_en = pairwise_energy.reshape((-1, H, W)) # Reshape just for plotting plt.figure(figsize=(15,5)) plt.subplot(1,3,1); plt.imshow(map_soln1); plt.title('MAP Solution with DenseCRF\n(5 steps, KL={:.2f})'.format(kl1)); plt.axis('off'); plt.subplot(1,3,2); plt.imshow(map_soln2); plt.title('MAP Solution with DenseCRF\n(20 steps, KL={:.2f})'.format(kl2)); plt.axis('off'); plt.subplot(1,3,3); plt.imshow(map_soln3); plt.title('MAP Solution with DenseCRF\n(50 steps, KL={:.2f})'.format(kl3)); plt.axis('off');
返回:

这个不太好看出效果,下面:

可见50次迭代后效果很好





