FIR滤波原理及verilog设计

FIR（Finite Impulse Response）Filter：有限冲激响应滤波器，又称为非递归线性滤波器。

FIR滤波器的冲击响应是一个值为滤波器抽头系数的采样序列，其脉冲响应由有限个采样值构成。长度（抽头数）为N+1、阶数为N的FIR系统的转移函数。

FIR滤波器是如何滤波的？

信号通过一个FIR滤波器其实就是信号与FIR滤波器的系数进行卷积（即移位相乘再累加）的过程。但是很多书上却喜欢用很复杂的文字和公式来描述这个本来很简单的概念，唯恐读者感受不到他们的书的高大上！
简单信号模型
低频信号：即在时域上变化慢的信号，如1 1 1 1 2 2 2 2，还有直流信号1 1 1 1 1 1 1
高频信号：即在时域上变化快的信号，如1 2 1 2 1 2 1 2
简单的滤波器模型
低通滤波器：1 1
高通滤波器：1 -1

用滤波器模型对高频或者低频信号进行卷积可以很明显的看出来滤波器对高低频信号的过滤。数字滤波器是在时间序列中工作的，接受一个离散的，有限长度的自序列，产生一个输出序列。

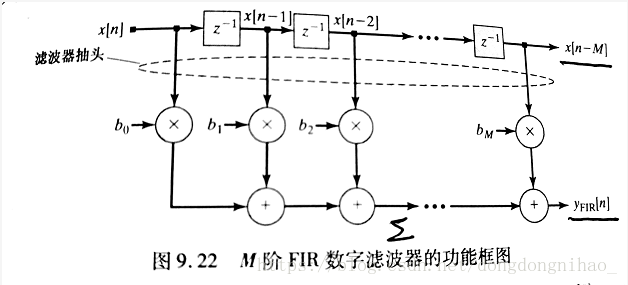
FIR滤波器可以用下图所示的z域功能模块图来描述，其中有z^-1的方框都代表了有一个时钟周期延时的寄存器单元，一个M阶的FIR滤波器有M+1个抽头，通过移位寄存器用每个时钟边沿n（时间下标）处的数据流采样值乘以抽头系数，并将他们加起来形成输出y fir{n}。

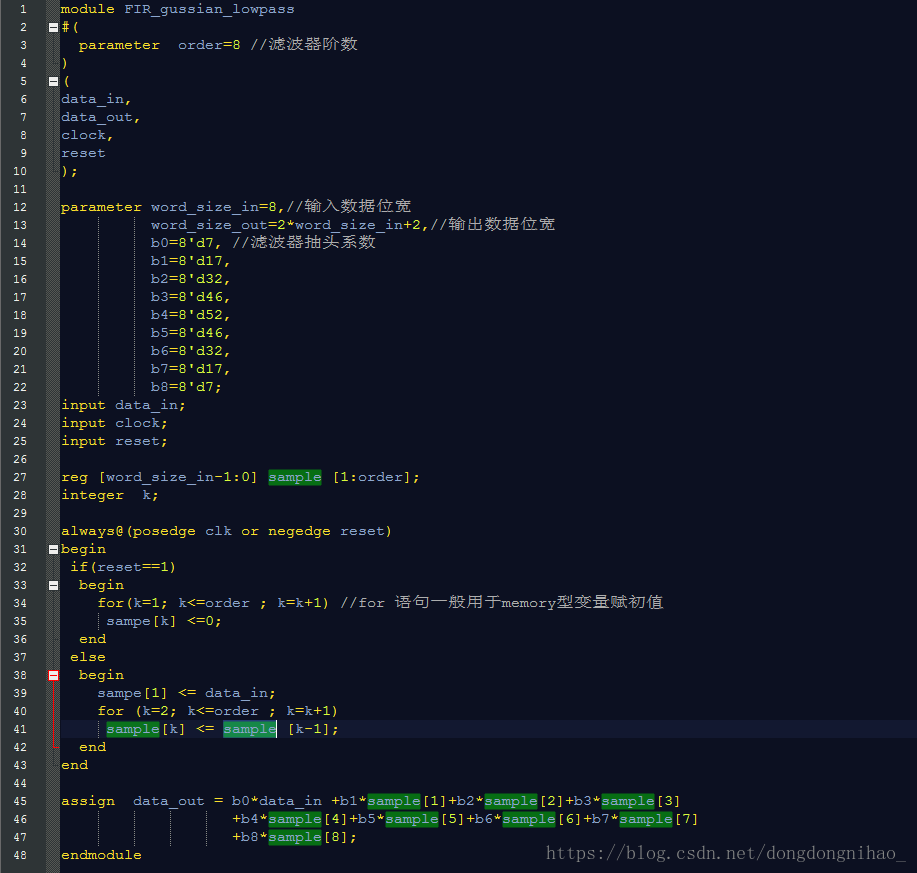
这个功能框图的verilog描述如下：

生成滤波器抽头系数可以使用matlab辅助生成，具体请参考：https://blog.csdn.net/qq_27745395/article/details/76509614

代码中为高斯低通滤波器系数