循环神经网络模型
整理并翻译自吴恩达深度学习系列视频：序列模型第一周，有所详略。
Recurrent Neural Network
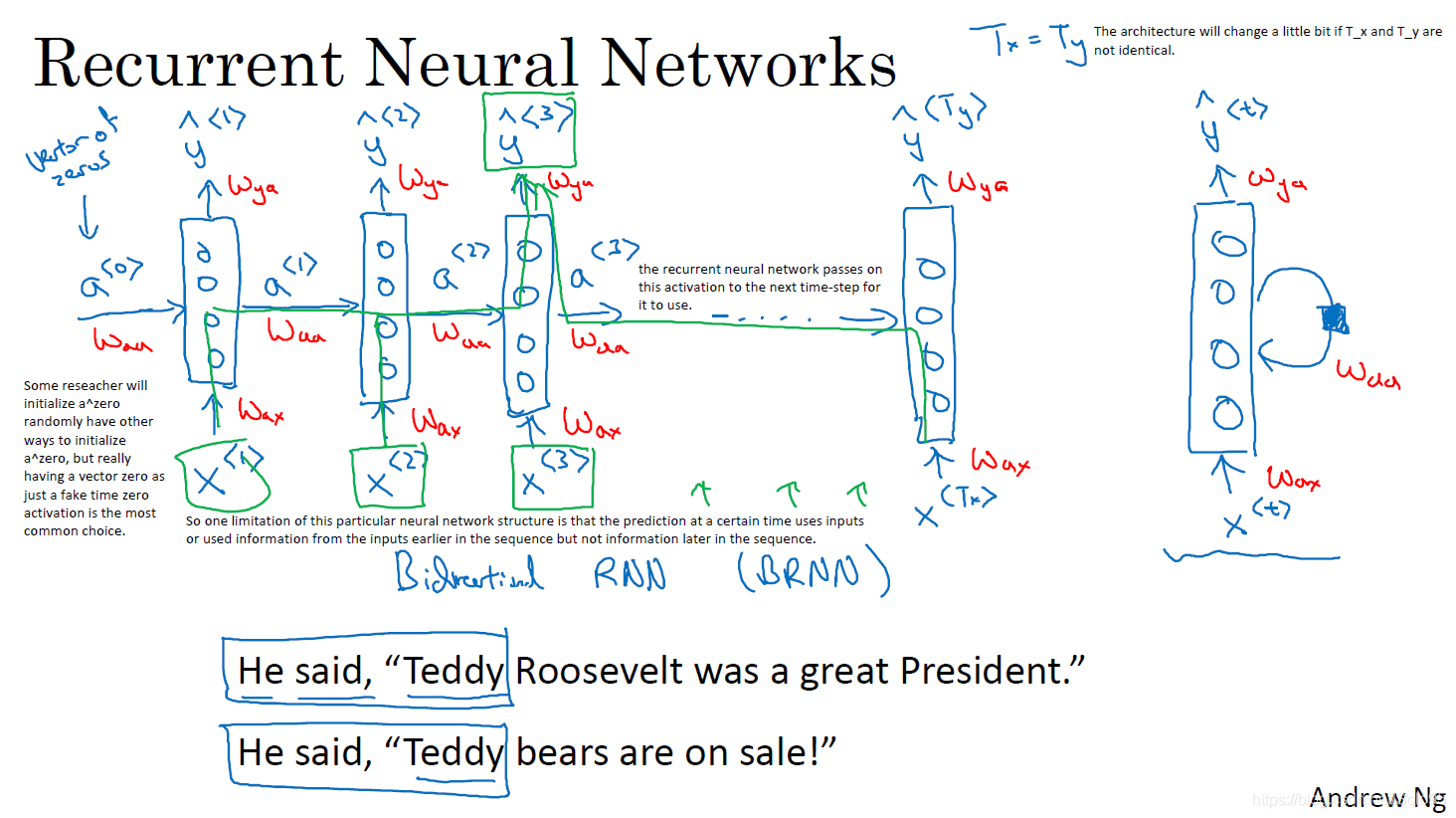一个标准的循环神经网络如图所示，在网络的每一个时间步
t
t
t，它接受前一层的激活函数值
a
<
t
−
1
>
a^{<t-1>}
a<t−1>和输入
x
<
t
>
x^{<t>}
x<t>， 使用权值矩阵使用
W
a
a
W_{aa}
Waa和
W
a
x
W_{ax}
Wax计算
a
<
t
>
a^{<t>}
a<t>，使用结果
a
<
t
>
a^{<t>}
a<t>和权值矩阵
W
y
a
W_{ya}
Wya计算
y
^
<
t
>
\hat{y}^{<t>}
y^<t>，计算方法如第二小节。
Forward Propagation
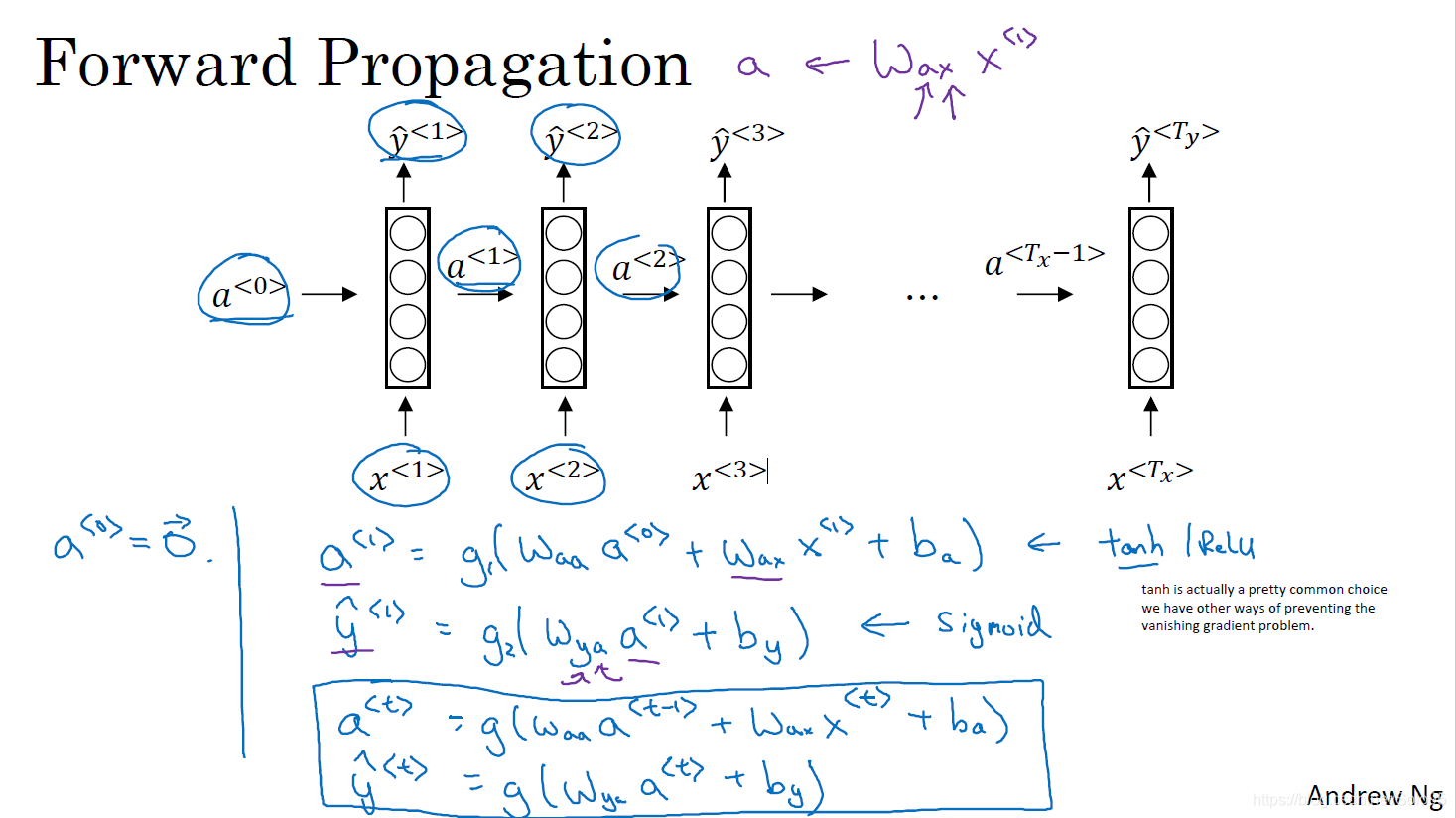
可总结为以下：
a
<
t
>
=
g
1
(
W
a
a
a
<
t
−
1
>
+
W
a
x
x
<
t
>
+
b
a
)
a^{<t>}=g_1(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)
a<t>=g1(Waaa<t−1>+Waxx<t>+ba)
y
^
<
t
>
=
g
2
(
W
y
a
a
<
t
>
+
b
y
)
\hat{y}^{<t>}=g_2(W_{ya}a^{<t>}+b_y)
y^<t>=g2(Wyaa<t>+by)
g
1
g_1
g1可以使用
t
a
n
h
tanh
tanh、
R
e
L
u
ReLu
ReLu，
g
2
g_2
g2可以使用
s
i
g
m
o
i
d
sigmoid
sigmoid。
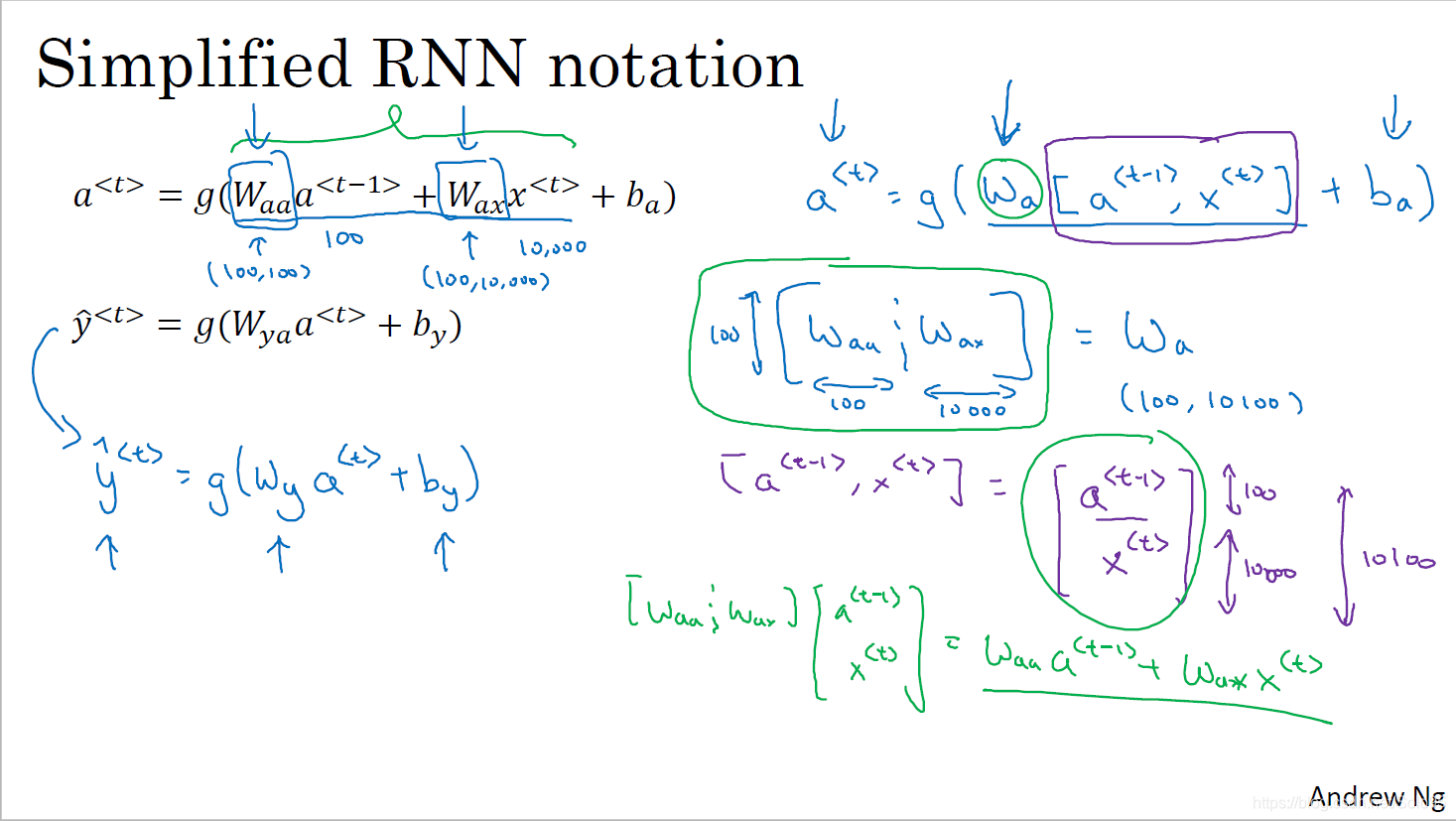
上图右边是向量化版本的实现，它将两个参数矩阵横向堆砌成
[
W
a
a
∣
W
a
x
]
[W_{aa}|W_{ax}]
[Waa∣Wax]构成
W
a
W_a
Wa，将两个输入纵向堆砌成
[
a
<
t
−
1
>
x
<
t
>
]
[\frac{a^{<t-1>}}{x^{<t>}}]
[x<t>a<t−1>](横线表示分隔符不是除法)。
Backward Propagation
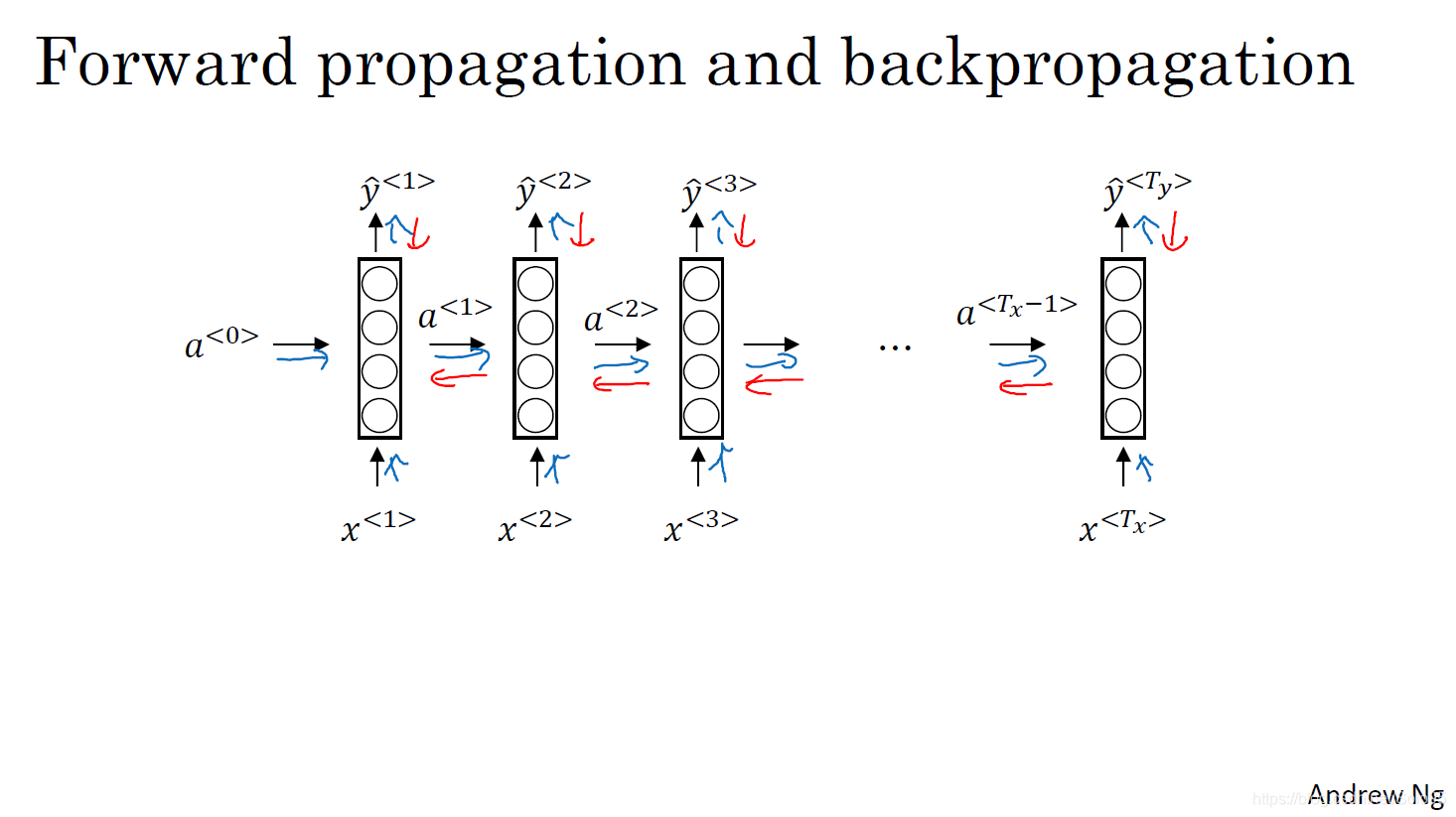
循环神经网络的反向传播同其他网络一致，按反方向计算导数，编程时框架会自动帮我们处理反向传播，但了解其基本原理也是有助益的。
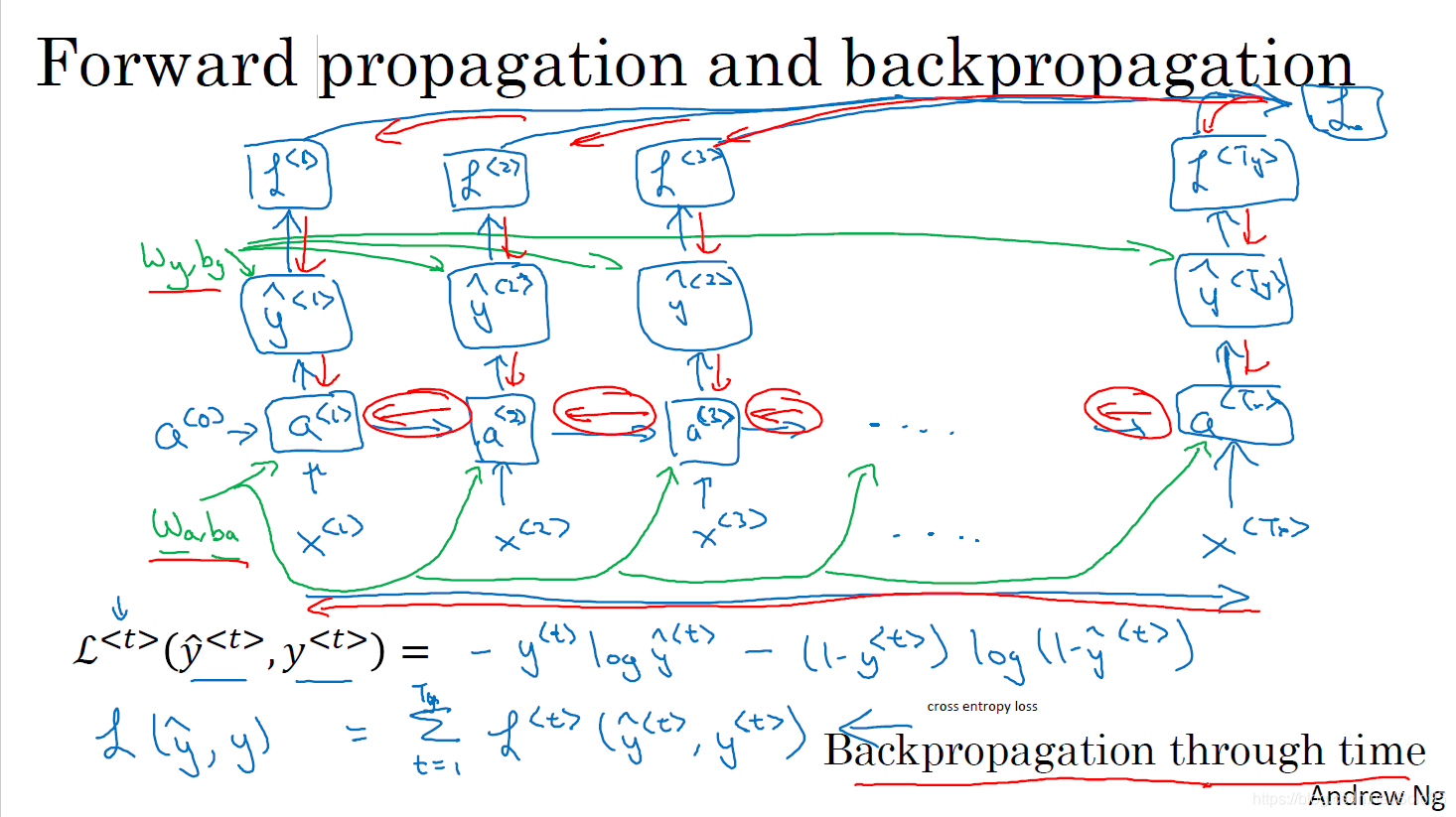
如上图所示，需注意，每一个横向上的参数矩阵是共享的，
W
y
、
b
y
W_y、b_y
Wy、by用于每次计算
y
<
t
>
^
\hat{y^{<t>}}
y<t>^，
W
a
、
b
a
W_a、b_a
Wa、ba也用于每次计算
x
<
t
>
x^{<t>}
x<t>。
其损失函数使用的是交叉熵(cross entropy loss)。
L
<
t
>
(
y
^
<
t
>
,
y
<
t
>
)
=
−
y
<
t
>
l
o
g
y
^
<
t
>
−
(
1
−
y
<
t
>
)
l
o
g
(
1
−
y
^
<
t
>
)
)
\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})=-y^{<t>}log\hat{y}^{<t>}-(1-y^{<t>})log(1-\hat{y}^{<t>}))
L<t>(y^<t>,y<t>)=−y<t>logy^<t>−(1−y<t>)log(1−y^<t>))
L
(
y
^
<
t
>
,
y
)
=
∑
t
=
1
T
L
<
t
>
(
y
^
<
t
>
,
y
<
t
>
)
\mathcal{L}(\hat{y}^{<t>},y)=\sum_{t=1}^{T}\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})
L(y^<t>,y)=t=1∑TL<t>(y^<t>,y<t>)
其他种类的RNN
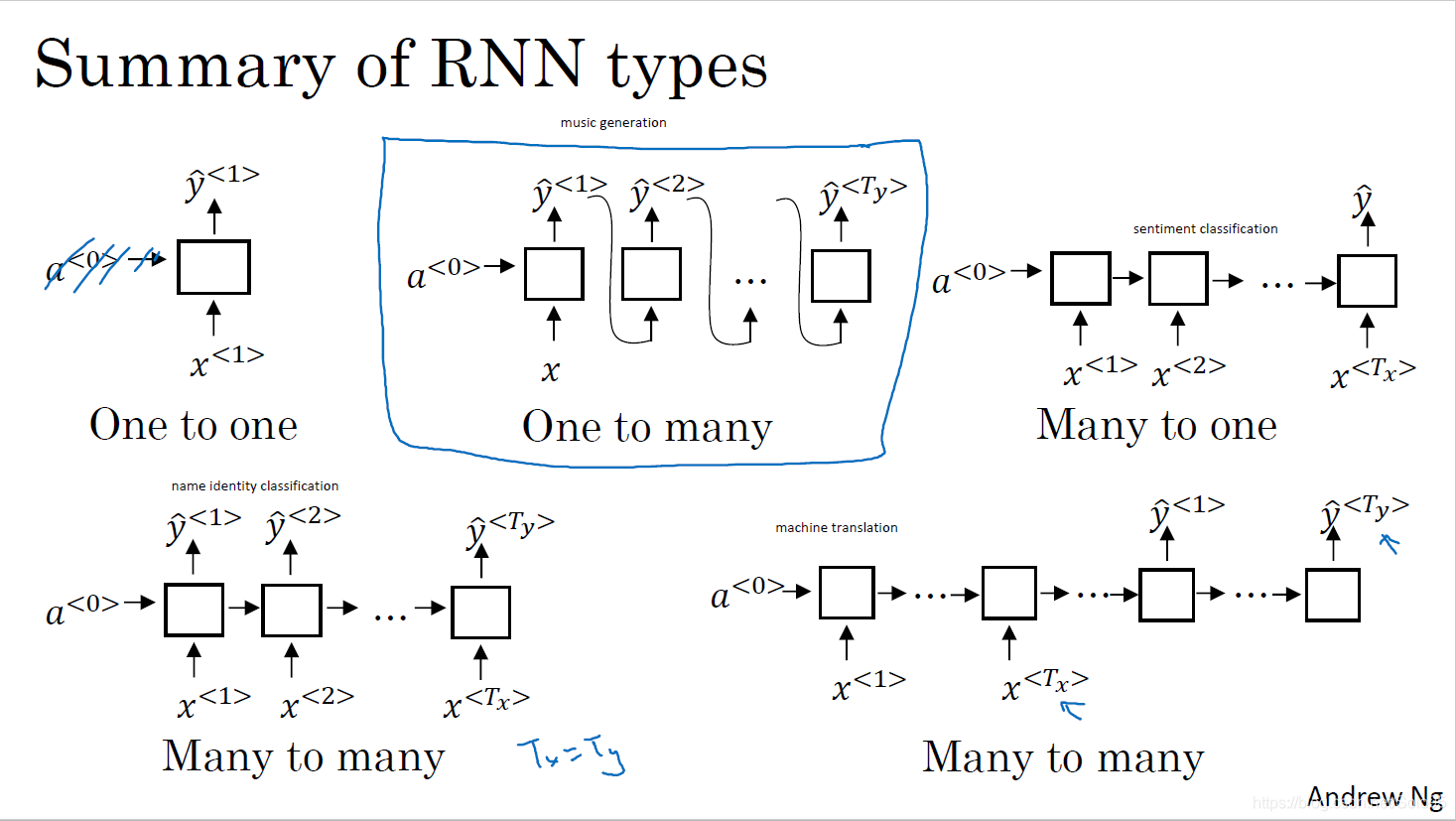
根据输入和输出的对应关系，RNN有图示几种结构，即一对一、一对多、多对一、多堆多。
