Gated Recurrent Unit(GRU)
整理并翻译自吴恩达深度学习系列视频:序列模型第一周,有所详略。
Gated Recurrent Unit(GRU)
Gated Recurrent Unit(GRU), which is a modification to the RNN hidden layer that makes it much better at capturing long range connections and helps a lot with the vanishing gradient problem.
Vanishing gradients AND Exploding gradients with RNNs
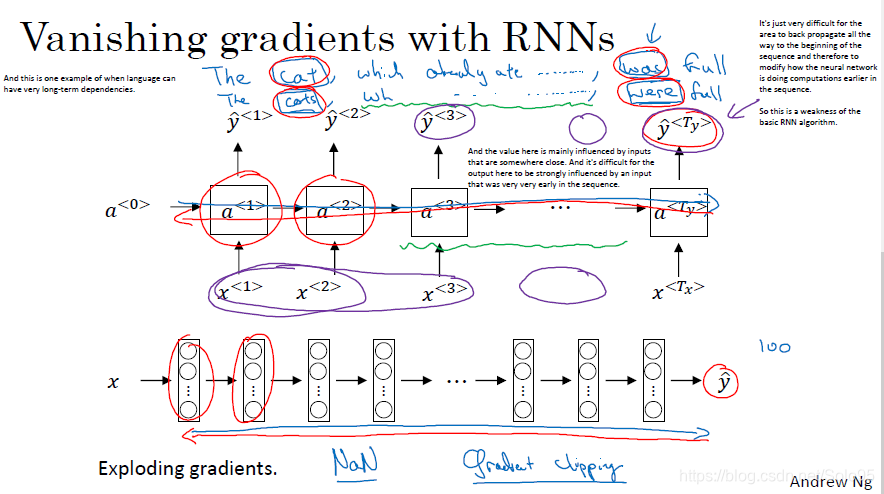
标准的RNN结构面临着2个很严重的问题。一是梯度消失和梯度爆炸;二是计算某个
y
^
<
t
>
\hat{y}^{<t>}
y^<t>时,只用到了前面的输入,尤其是是靠近
y
^
<
t
>
\hat{y}^{<t>}
y^<t>的输入,非常靠前的输入和后面的输入对结果产生的影响微乎其微。
第一个问题非常好理解,与CNN相同,当网络很深时,反向传播就很难从后向前对网络的前几层在计算序列上产生影响,越往前计算出的导数越小直至0,这是很直观的梯度消失问题。偶尔也会遇到梯度爆炸的问题,即计算出的导数越来越大。这是基本RNN结构的缺点。
第二个问题,在判断"Cat eat a lot of things,…, which was full."和"Cats eat a lot of things,…,which were full."两个句子的which后面到底应该跟单数还是复数形式时,显然需要考虑到第一个单词是cat还是cats,但是由于输出which后的单词时,普通的RNN结构很难保留第一个单词产生的影响在此时发挥作用,因此引入了GRU单元或LTSM单元来解决这个问题。
在对"He said, “Teddy bears are on sale!” "和"He said, “Teddy Roosevelt was a great President!”"做命名实体判别时,需要知道Teddy后一个单词是什么,普通的RNN结构显然没有这种能力,因此引入了双向循环网络解决这一问题。
这篇文章仅介绍GRU,LTSM和双向神经网络参见:
Long Short term memory unit(LSTM)
GRU unit
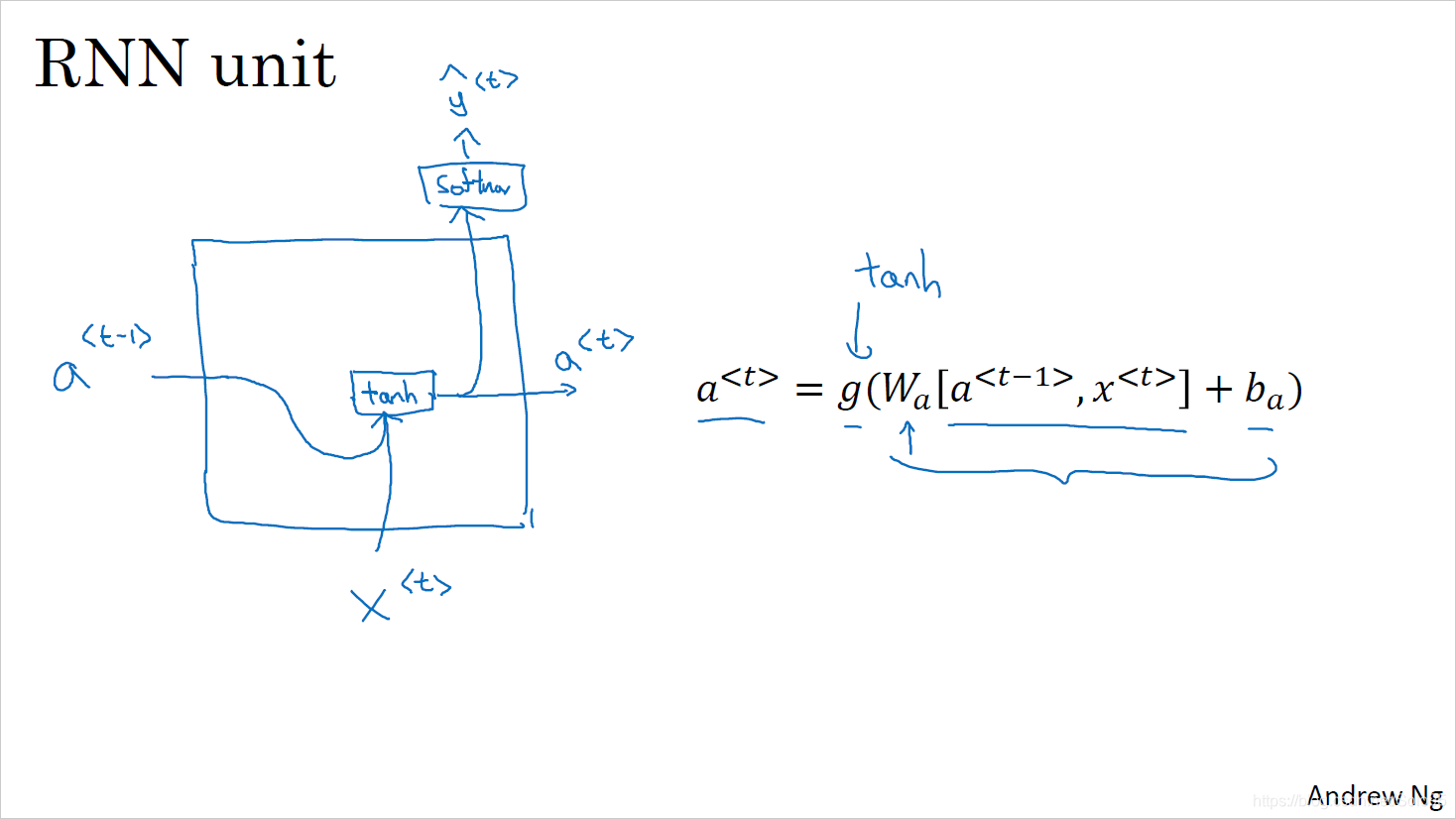
普通的RNN unit如上图所示,一个简化了的GRU unit如下图所示:
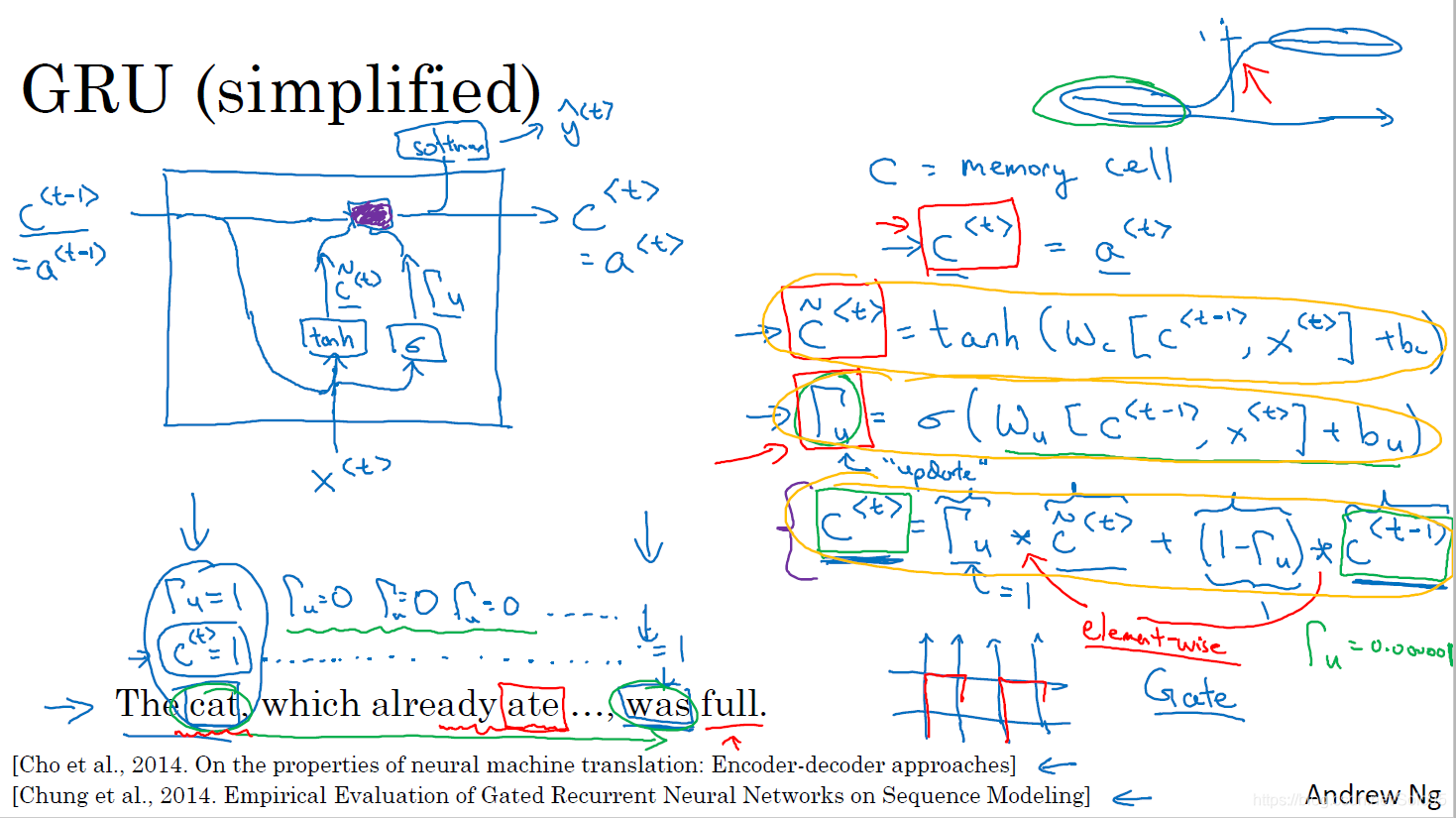
GRU里首先引入了一个新的变量C作为memory cell使用,即保留一些前面的层中的某些有价值的信息。
GRU里的Gated是指我们引入了门控,即使用 Γ u \Gamma_u Γu来决定我们是否使用当前层计算出的 C ~ < t > \tilde{C}^{<t>} C~<t>来更新C。
C < t > = a < t > C^{<t>}=a^{<t>} C<t>=a<t>
C
~
<
t
>
=
t
a
n
h
(
W
c
[
C
<
t
−
1
>
,
x
<
t
>
]
+
b
c
)
\tilde{C}^{<t>}=tanh(W_c[C^{<t-1>}, x^{<t>}]+b_c)
C~<t>=tanh(Wc[C<t−1>,x<t>]+bc)
Γ
u
=
σ
(
W
u
[
C
<
t
−
1
>
,
x
<
t
>
]
+
b
u
)
\Gamma_u=\sigma(W_u[C^{<t-1>}, x^{<t>}]+b_u)
Γu=σ(Wu[C<t−1>,x<t>]+bu)
C
<
t
>
=
Γ
u
∗
C
~
<
t
>
+
(
1
−
Γ
u
)
∗
C
<
t
−
1
>
C{<t>}=\Gamma_u*\tilde{C}^{<t>}+(1-\Gamma_u)*C^{<t-1>}
C<t>=Γu∗C~<t>+(1−Γu)∗C<t−1>
门控值
Γ
u
=
1
\Gamma_u=1
Γu=1时,用的是新的值
C
~
\tilde{C}
C~;门控值
Γ
u
=
0
\Gamma_u=0
Γu=0时,用的是前一层的值
C
<
t
−
1
>
C^{<t-1>}
C<t−1>
完整的GRU计算公式如下:

C
~
<
t
>
=
t
a
n
h
(
Γ
r
∗
W
c
[
C
<
t
−
1
>
,
x
<
t
>
]
+
b
c
)
\tilde{C}^{<t>}=tanh(\Gamma_r*W_c[C^{<t-1>}, x^{<t>}]+b_c)
C~<t>=tanh(Γr∗Wc[C<t−1>,x<t>]+bc)
Γ
u
=
σ
(
W
u
[
C
<
t
−
1
>
,
x
<
t
>
]
+
b
u
)
\Gamma_u=\sigma(W_u[C^{<t-1>}, x^{<t>}]+b_u)
Γu=σ(Wu[C<t−1>,x<t>]+bu)
Γ
r
=
σ
(
W
r
[
C
<
t
−
1
>
,
x
<
t
>
]
+
b
r
)
\Gamma_r=\sigma(W_r[C^{<t-1>}, x^{<t>}]+b_r)
Γr=σ(Wr[C<t−1>,x<t>]+br)
C
<
t
>
=
Γ
u
C
~
<
t
>
+
(
1
−
Γ
u
)
C
<
t
−
1
>
C{<t>}=\Gamma_u\tilde{C}^{<t>}+(1-\Gamma_u)C^{<t-1>}
C<t>=ΓuC~<t>+(1−Γu)C<t−1>
注意,这里引入了第二个门控值 Γ r \Gamma_r Γr来衡量 C ~ < t > \tilde{C}^{<t>} C~<t>和 C < t − 1 > {C}^{<t-1>} C<t−1>之间的相关程度,计算该值使用了与 Γ u \Gamma_u Γu不同的参数矩阵。除此之外,在计算 C ~ < t > \tilde{C}^{<t>} C~<t>也使用了 Γ r \Gamma_r Γr。




