从Markov Process到Markov Decision Process
Recall: Markov Property
information state: sufficient statistic of history
State
s
t
s_t
st is Markov if and only if:
p
(
s
t
+
1
∣
s
t
,
a
t
)
=
p
(
s
t
+
1
∣
h
t
,
a
t
)
p(s_{t+1}|s_t,a_t)=p(s_{t+1}|h_t,a_t)
p(st+1∣st,at)=p(st+1∣ht,at)
Future is independent of past given present
Markov Process or Markov Chain
无记忆性随机过程
- 具有马尔科夫性质的随机状态的序列
马尔科夫过程(Markov Process)的定义:
- S是一个(有限)的状态集(s ∈ S \in S ∈S)
- P是动态/变迁模型,它指定了 p ( s t + 1 = s ′ ∣ s t = s ) p(s_{t+1}=s'|s_t=s) p(st+1=s′∣st=s)
注意:没有奖励(reward),也没有动作(actions)
如果状态数(N)是有限的,可以把P表示成一个矩阵:

Markov Reward Process (MRP)
马尔科夫奖励过程 = 马尔科夫过程 + 奖励
马尔科夫奖励过程(MRP)的定义:
- S是一个状态的有限集(s ∈ \in ∈ S)
- P是动态/变迁模型,它指定了 P ( s t + 1 = s ′ ∣ s t = s ) P(s_{t+1}=s'|s_t=s) P(st+1=s′∣st=s)
- R是一个奖励函数 R ( s t = s ) = E [ r t ∣ s t = s ] R(s_t=s)=\mathbb{E}[r_t|s_t=s] R(st=s)=E[rt∣st=s]
- 折扣因子 γ ∈ [ 0 , 1 ] \gamma \in[0,1] γ∈[0,1]
注意:没有动作
如果状态数(N)有限,R可以被表示成一个向量。
Return & Value Function
窗口(horizon)的定义:
- 每一轮(episode)的时间步数目
- 可以是有限的
- 也被称作有限马尔科夫奖励过程
返回(return)的定义:
- 从t开始长达整个窗口的打折奖励总和:
G t = r t + γ r t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+\gamma r_{t+1}+\gamma^2r_{t+2}+\gamma^3r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+γ3rt+3+...
状态奖励方程(State Value Function foe a MRP)的定义:
- 从状态s开始的返回的期望
V ( s ) = E [ G t ∣ s t = s ] = E [ r t + γ r t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . ∣ s t = s ] V(s) = \mathbb{E}[G_t|s_t=s]=\mathbb{E}[r_t+\gamma r_{t+1}+\gamma^2r_{t+2}+\gamma^3r_{t+3}+...|s_t=s] V(s)=E[Gt∣st=s]=E[rt+γrt+1+γ2rt+2+γ3rt+3+...∣st=s]
如果过程是确定的,那么返回和奖励是相等的;大部分情况下过程是随机的,它们会是不同的。
Discount Factor
折扣因子一方面是由于被启发创造的,另一方面也是为了数学上的方便。
- 数学上的方便(避免无限的返回(函数)和价值(函数))
- 人类通常是以折扣因子小于1的方式行动的
- γ = 0 \gamma=0 γ=0仅关心即时奖励
- γ = 1 \gamma=1 γ=1未来奖励将等于即时奖励
- 如果一轮(episode)的长度一直是有限的,可以使用 γ = 1 \gamma=1 γ=1
Computing the Value of a Markov Reward Process
- 可以通过仿真(simulation)来估计
实验平均接近真实期望值的准确度大致在 1 n \frac{1}{\sqrt{n}} n1,n代表仿真次数。 - 对返回取平均
- 专注不等式(Concentration inequalities)限定专注于期望值的速度
- 不需要对马尔科夫结构做出假设
但是上述过程没有利用任何world是马尔科夫的这个事实。为了得到更好的估计有额外的结构。
- 马尔科夫性质产生额外的结构。
(the future is independent of past given present) - MRP的价值函数满足
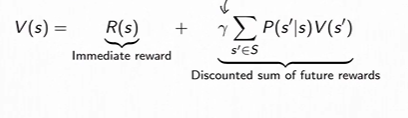
矩阵形式

然后就可以以解析方式求解:
V
=
R
+
γ
P
V
V=R+\gamma PV
V=R+γPV
V
−
γ
P
V
=
R
V-\gamma PV = R
V−γPV=R
(
I
−
γ
P
)
V
=
R
(I - \gamma P) V = R
(I−γP)V=R
V
=
(
I
−
γ
P
)
−
1
R
V = (I -\gamma P)^{-1} R
V=(I−γP)−1R
直接求解的算法复杂度是 O ( n 3 ) O(n^3) O(n3)
矩阵P必须是定义良好即能求逆的。在以上过程中,我们假定是固定的horizon,价值函数是固定的,所以状态的下一个状态可以指向自己,self-loop是允许存在的。
一定可以求逆吗?
因为P是马尔科夫矩阵(随机矩阵),那么它的特征值将总是小于等于1,如果折扣因子小于1,那么 I − γ P I-\gamma P I−γP总是可逆的(证明略,感兴趣的朋友可以去查一下,博主数学不是很好。)。
Iterative Algorithm for Computing Value of a MRP
另一种求解方法是动态规划:
Initializa V 0 ( s ) = 0 V_0(s) = 0 V0(s)=0 for all s
For k = 1 until convergence
For all s in S
V k ( s ) = R ( s ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V k − 1 ( s ′ ) V_k(s) = R(s) + \gamma \sum_{s^{'} \in S}P(s^{'}|s)V_{k-1}(s^{'}) Vk(s)=R(s)+γs′∈S∑P(s′∣s)Vk−1(s′)
计算复杂度:
O
(
∣
s
∣
2
)
O(|s|^2)
O(∣s∣2) for each iteration (|S| = N)
收敛的条件通常使用范数来衡量,即
∣
V
k
−
V
k
−
1
∣
<
ϵ
|V_k - V_{k-1}| < \epsilon
∣Vk−Vk−1∣<ϵ
这种计算方式的优势在于每次迭代平方复杂度,并且还有一些稍后会提及的引入actions之后的增益。
总结起来,计算MRP的价值有三种方法:
- 模拟仿真(Simulation)
- 解析求解(Analytic solve, requires us a step, a finite set of states)
- 动态规划(DP)
Markov Decision Proces(MDP)
MDP = MRP + actions.
MDP的定义,MDP是一个五元组(quintuple)(S,A,P,R, γ \gamma γ):
- S 是一个有限的马尔科夫状态集 s ∈ S s \in S s∈S
- A 是一个有限的动作集 a ∈ A a \in A a∈A
- P 是针对每一个动作的动态/迁移模型,它指定了 P ( s t + 1 = s ′ ∣ s t = s , a t = a ) P(s_{t+1}=s' | s_t = s, a_t = a) P(st+1=s′∣st=s,at=a)
- R是一个奖励函数(回报函数)
R ( s t = s , a t = a ) = E [ r t ∣ s t − s , a t = a ] R(s_t = s, a_t = a) = \mathbb{E}[r_t|s_t - s, a_t = a] R(st=s,at=a)=E[rt∣st−s,at=a] - 折扣因子 γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]
MDP Policies
- 策略(Policy)指定了在每一个状态采取什么动作
- 可以是确定性的也可以是随机的
- 更一般性,把策略考虑成一种条件分布
-给定一个状态,指定一个动作上的分布 - Policy: π ( a ∣ s ) = P ( a t = a ∣ s t = s ) \pi(a|s) = P(a_t = a | s_t = s) π(a∣s)=P(at=a∣st=s)
MDP + Policy
MDP + Policy可以指定一个Markov Reward Process,因为Policy里指定了每个状态的动作,MDP就坍缩成了MRP。
更确切的讲,它们指定的是
M
R
P
(
S
,
R
π
,
P
π
,
γ
)
MRP(S, R^\pi, P^\pi, \gamma)
MRP(S,Rπ,Pπ,γ):
R
π
=
∑
a
∈
A
π
(
a
∣
s
)
R
(
s
,
a
)
R^\pi=\sum_{a \in A}\pi(a|s)R(s,a)
Rπ=∑a∈Aπ(a∣s)R(s,a)
P
π
(
s
′
∣
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
P
(
s
′
∣
s
,
a
)
P^\pi(s'|s) = \sum_{a \in A}\pi(a|s)P(s'|s,a)
Pπ(s′∣s)=∑a∈Aπ(a∣s)P(s′∣s,a)
这隐含着,只要你有确定的策略,我们可以使用前述的所有用来计算MRP的价值的相同方法,通过使用定义一个 R π R^\pi Rπ和 P π P^\pi Pπ,来计算MDP的一个策略的价值。
MDP Policy Evaluation, Iterative Algorithm
Initialize V 0 ( s ) = 0 V_0(s) = 0 V0(s)=0 for all s
For k = 1 until convergence
For all s in S
V k π ( s ) = r ( s , π ( s ) ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , π ( s ) ) V k − 1 π ( s ′ ) V_k^\pi(s) = r(s,\pi(s)) + \gamma\sum_{s' \in S}p(s'|s,\pi(s))V_{k-1}^\pi(s') Vkπ(s)=r(s,π(s))+γ∑s′∈Sp(s′∣s,π(s))Vk−1π(s′)
对于一个特定的策略来说,这是一个Bellman backup。
在RL文献中,上面等式的右边被称作"Bellman backup"。状态或状态 - 动作对的Bellman backup是Bellman方程的右侧:即时奖励加下一个值,这是一个迭代的过程,因此叫backup。
仔细对比一下,跟前面所述MRT计算价值是一样的,只不过因为有固定的策略,所以我们使用策略来索引奖励。即为了学习一个特定策略的价值,我们通过总是采取策略所指定的动作来初始化价值函数。
练习 计算一步迭代

V
k
+
1
(
s
6
)
=
r
(
s
6
)
+
γ
∗
(
0.5
∗
0
+
0.5
∗
10
)
V_{k+1}(s_6)=r(s_6)+\gamma*(0.5*0+0.5*10)
Vk+1(s6)=r(s6)+γ∗(0.5∗0+0.5∗10)
V
k
+
1
(
s
6
)
=
0.5
∗
(
0.5
∗
10
)
=
2.5
V_{k+1}(s_6)=0.5*(0.5*10)=2.5
Vk+1(s6)=0.5∗(0.5∗10)=2.5
这个真的很简单,单纯的代公式,只要前面所述内容你都记住了,就直接能理解。




