Monte Carlo(MC) Policy Evaluation 蒙特·卡罗尔策略评估
这篇博文是另一篇博文Model-Free Policy Evaluation 无模型策略评估的一个小节,因为 蒙特·卡罗尔策略评估本身就是一种无模型策略评估方法,原博文有对无模型策略评估方法的详细概述。
简单而言, 蒙特·卡罗尔策略评估是依靠在给定策略下使智能体运行多个轮次并采样对回报取平均值近似期望来更新对价值的估计,根据大数定理,采样的轮次越多,估计值越接近真实值。
相关基础概念

- 如果我们不知道动态模型P/或奖励模型R呢?
- 新内容:在没有模型的条件下进行策略价值评估
- 给定数据/或与环境交互的能力
- 足够计算策略 π \pi π的合理估计
Monte Carlo(MC) Policy Evaluation
蒙特·卡罗尔策略评估
- G t = r t + γ r t + 1 + γ 2 r t + 2 + r 3 γ r t + 3 + . . . G_t = r_t+\gamma r_{t+1}+\gamma^2r_{t+2}+r^3\gamma r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+r3γrt+3+... in MDP M under policy π \pi π
-
V
π
(
s
)
=
E
T
∼
π
[
G
t
∣
s
t
=
s
]
V^\pi(s)=\mathbb{E}_{\Tau \sim \pi}[G_t|s_t=s]
Vπ(s)=ET∼π[Gt∣st=s]
- 遵循策略 π \pi π产生的迹(trajectories) T \Tau T(希腊字母tau)上的期望
迹(trajectories)想表达的是执行路径的意思,其实也可以翻译成路径,但形式化领域惯用迹这种说法。
-
简单的理解思路:价值 = 回报的平均(Value = mean return)
-
如果所有的迹都是有限的,那么我们在迹的集合中采样并计算平均回报
-
不需要MDP的动态模型/回报模型
-
不需要bootstrapping
-
不需要假设状态是马尔科夫的
-
只能被应用于周期化(可以重复进行多次的意思)的MDPs
- 在一个完整的一轮(episode)中取平均
- 需要每一轮都能终止
Monte Carlo(MC) Policy Evaluation
- 目标:在策略
π
\pi
π下给定的所有轮次下估计
V
π
V^\pi
Vπ
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s_1,a_1,r_1,s_2,a_2,r_2,... s1,a1,r1,s2,a2,r2,...其中的动作都是在策略 π \pi π中采样得到的。
- G t = r t + γ r t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+\gamma r_{t+1}+\gamma^2r_{t+2}+\gamma^3r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+γ3rt+3+... in MDP M under policy π \pi π
- V π ( s ) = E π [ G t ∣ s t = s ] V^\pi(s) = \mathbb{E}_\pi[G_t|s_t=s] Vπ(s)=Eπ[Gt∣st=s]
- MC计算实验平均回报
- 通常是通过一个递增的风格实现的
- 在每一轮之后,更新 V π V^\pi Vπ的估计
First-Visit Monte Carlo(MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0\ \forall s \in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,\Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+\gamma r_{i, t+1} + \gamma^2r_{i, t+2}+...+\gamma^{\Tau_i-1}r_{i,\tau_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For each state s visited in episode i
- For first time t that state s is visited in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Increment total return G ( s ) = G ( s ) + G i , t G(s)=G(s)+G_{i,t} G(s)=G(s)+Gi,t
- Update estimate V π ( s ) = G ( s ) / N ( s ) V_\pi(s) = G(s)/N(s) Vπ(s)=G(s)/N(s)
- For first time t that state s is visited in episode i
Bias, Variance and MSE
深度学习的概率基础,这里复习一下,因为要衡量估计的好坏,不懂的话参见深度学习那本花书。
- 考虑一个被 θ \theta θ参数化的统计模型,它决定了在观测数据上的概率分布 P ( x ∣ θ ) P(x|\theta) P(x∣θ)
- 考虑一个统计
θ
^
\hat{\theta}
θ^,它提供了
θ
\theta
θ的一个估计并且它是观测数据x上的一个函数
- 比如。对于一个未知方差的高斯分布,独立同分布(iid,independently identically distribution) 数据点的平均值是对高斯分布平均的一个估计
- 定义:估计
θ
^
\hat{\theta}
θ^的bias是:
B i a s θ ( θ ^ ) = E x ∣ θ [ θ ^ ] − θ Bias_\theta(\hat{\theta})=\mathbb{E}_{x|\theta}[\hat{\theta}]-\theta Biasθ(θ^)=Ex∣θ[θ^]−θ - 定义:估计
θ
^
\hat{\theta}
θ^的Variance是:
V a r ( θ ^ ) = E x ∣ θ [ ( θ ^ − E [ θ ^ ] ) 2 ] Var(\hat{\theta})=\mathbb{E}_{x|\theta}[(\hat{\theta}-\mathbb{E}[\hat{\theta}])^2] Var(θ^)=Ex∣θ[(θ^−E[θ^])2] - 定义:估计
θ
^
\hat{\theta}
θ^的均方误差(MSE)是:
M S E ( θ ^ ) = V a r ( θ ^ ) + B i a s ( θ ^ ) 2 MSE(\hat{\theta})=Var(\hat{\theta})+Bias(\hat{\theta})^2 MSE(θ^)=Var(θ^)+Bias(θ^)2
M S E ( θ ^ ) = E x ∣ θ [ ( ^ θ ) − θ ] 2 MSE(\hat{\theta})=\mathbb{E}_{x|\theta}[\hat(\theta)-\theta]^2 MSE(θ^)=Ex∣θ[(^θ)−θ]2 (按MSE的定义,博主补充的公式)
有了补充的知识后,在回头看上面的算法:

它有如下性质:
- V π V^\pi Vπ估计器是真实期望 E π [ G t ∣ s t = s ] \mathbb{E}_\pi[G_t|s_t=s] Eπ[Gt∣st=s]的一个无偏估计器
- 根据大数定理,当 N ( s ) → ∞ N(s)\rightarrow \infty N(s)→∞时, V π ( s ) → E π [ G t ∣ s t = t ] V^\pi(s)\rightarrow \mathbb{E}_\pi[G_t|s_t=t] Vπ(s)→Eπ[Gt∣st=t]
Concentration inqualities通常用于Variance。通常我们不知道确切的Bias,除非知道ground truth值。实践中有很多方法得到bias的估计:比较不同形式的参数模型、structural risk maximization。
Every-Visit Monte Carlo (MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0\ \forall s \in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,\Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+\gamma r_{i, t+1} + \gamma^2r_{i, t+2}+...+\gamma^{\Tau_i-1}r_{i,\tau_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For each state s visited in episode i
- For every time t that state s is visited in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Increment total return G ( s ) = G ( s ) + G i , t G(s) = G(s) + G_{i,t} G(s)=G(s)+Gi,t
- Update estimate V π ( s ) = G ( s ) / N ( s ) V^\pi(s)=G(s)/N(s) Vπ(s)=G(s)/N(s)
- For every time t that state s is visited in episode i
它有如下性质:
- V π V^\pi Vπevery-visit MC估计器是真实期望 E π [ G t ∣ s t = s ] \mathbb{E}_\pi[G_t|s_t=s] Eπ[Gt∣st=s]的一个无偏估计器
- 但是一致性估计器(比如上面的First-Visit)通常会有更好的MSE误差
Incremental Carlo(MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0\ \forall s \in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,\Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+\gamma r_{i, t+1} + \gamma^2r_{i, t+2}+...+\gamma^{\Tau_i-1}r_{i,\tau_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For state s visited at time step t in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Update estimate
V π ( s ) = V π ( s ) N ( s ) − 1 N ( s ) + G i , t N ( s ) = V π ( s ) + 1 N ( s ) ( G i , t − V π ( s ) ) V^\pi(s)=V^\pi(s)\frac{N(s)-1}{N(s)}+\frac{G_{i,t}}{N(s)}= V^\pi(s)+\frac{1}{N(s)}(G_{i,t}-V^\pi(s)) Vπ(s)=Vπ(s)N(s)N(s)−1+N(s)Gi,t=Vπ(s)+N(s)1(Gi,t−Vπ(s))
注意比较前面以及上面以及下面算法的区别,没有了every-visit,变成了时间步t,即更新条件在不断改变,除此之外也在不断改变Update estimate的内容。
Incremental Carlo(MC) On Policy Evaluation Algorithm, Running Mean
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0\ \forall s \in S
G(s)=0 ∀s∈S
Loop
-
Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,\Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
-
Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+\gamma r_{i, t+1} + \gamma^2r_{i, t+2}+...+\gamma^{\Tau_i-1}r_{i,\tau_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
-
For state s visited at time step t in episode i
- For state s is visited at time step t in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Update estimate
V π ( s ) = V π ( s ) + α ( G i , t − V π ( s ) ) V^\pi(s)=V^\pi(s)+\alpha(G_{i,t}-V^\pi(s)) Vπ(s)=Vπ(s)+α(Gi,t−Vπ(s))
- For state s is visited at time step t in episode i
-
α = 1 N ( s ) \alpha=\frac{1}{N(s)} α=N(s)1时,和every-visit MC算法等同
-
α > 1 N ( s ) \alpha>\frac{1}{N(s)} α>N(s)1时,算法会忘掉旧数据,在non-stationary(非固定)领域非常有用
举一个例子,新闻推荐系统中,新闻是在不断变化着的,因此大家通常会重新训练以应对非固定过程(non-stationary)。
例题


Q1: V s 1 = V s 2 = V s 3 V_{s_1} = V_{s_2} = V_{s_3} Vs1=Vs2=Vs3, V s 4 = V s 5 = V s 6 = V s 7 = 0 V_{s_4}=V_{s_5}=V_{s_6}=V_{s_7}=0 Vs4=Vs5=Vs6=Vs7=0
为什么只有在 s 1 s_1 s1有回报1,其余都没有回报,但价值却是1呢。因为算法在整个轮次结束,最后一次更新V,这时候 G = 1 G=1 G=1,只有 s 1 s_1 s1、 s 2 s_2 s2、 s 3 s_3 s3三个状态被访问过,又因为使用的是First-Vist算法,所以,它们count都是1,那么 1 1 = 1 \frac{1}{1}=1 11=1
Q2: V s 2 = 1 V_{s_2}=1 Vs2=1
为什么,因为现在是Every-Visit,所以 s 2 s_2 s2的count是2,所以 2 2 = 1 \frac{2}{2}=1 22=1。
MC Policy Evaluation 图片概括描述
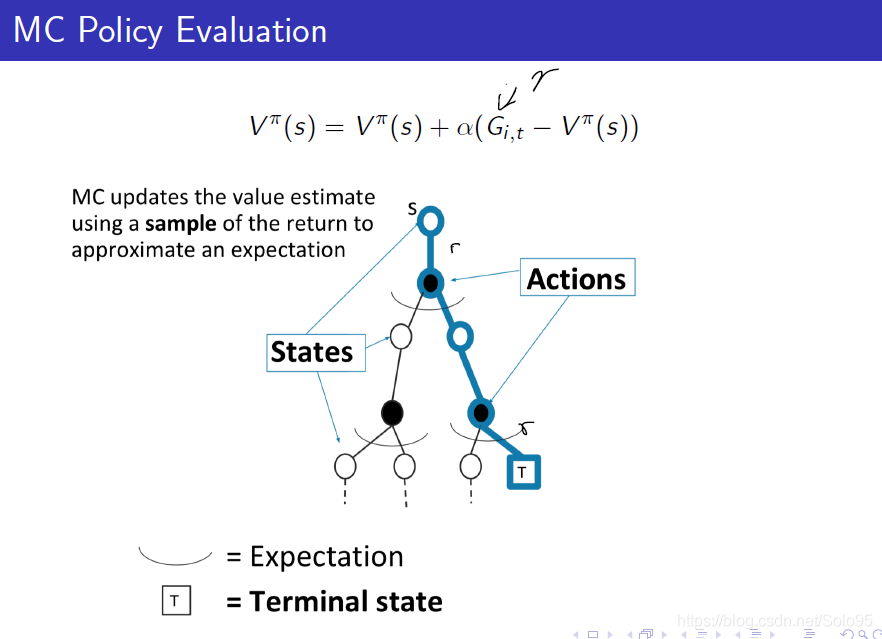
MC通过在整个迹上取近似平均(期望)来更新价值估计。
Monte Carlo (MC) Policy Evaluation Key Limitations
- 通常是个高方差估计器
- 降低这些方差需要大量数据
- 要求必须是可重复情景
- 一个轮次在该轮次的数据用于更新价值函数前该伦次必须能结束
Monte Carlo (MC) Policy Evaluation Summary
- 目标:在给定由于遵循策略
π
\pi
π而产生的所有轮次的条件下估计
V
π
(
s
)
V^\pi(s)
Vπ(s)
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s_1,a_1,r_1,s_2,a_2,r_2,... s1,a1,r1,s2,a2,r2,...其中动作a在策略 π \pi π下采样而来
- MDP M在遵循策略 π \pi π G t = r t + γ t t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+\gamma t_{t+1}+\gamma^2r_{t+2}+\gamma^3r_{t+3}+... Gt=rt+γtt+1+γ2rt+2+γ3rt+3+...
- V π ( s ) = E π [ G t ∣ s t = s ] V^\pi(s)=\mathbb{E}_\pi[G_t|s_t=s] Vπ(s)=Eπ[Gt∣st=s]
- 简单理解:依靠实验平均来估计期望(给定从我们所关心策略中采样得到的所有轮次)或者重新加权平均(Importance Sampling,即重要性采样)
- 更新价值估计是依靠使用一次回报的采样对期望进行近似
- 不使用bootstrapping
- 在某些假设(通常是温和假设)下收敛到真实值




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步