Monte Carlo Off Policy Evaluation
前面的一篇博文Monte Carlo(MC) Policy Evaluation 蒙特·卡罗尔策略评估 介绍的是On-Policy的策略评估。简而言之，On-Policy就是说做评估的时候就是在目标策略本身上做的评估，而Off-Policy指的是在别的策略上对目标策略做评估。
MC Off-Policy Evaluation
- 在某些领域(例如图示)尝试采取动作观察结果代价很大或者风险很高
- 因此我们希望能够根据以前的关于策略决策的旧数据和已有与之相关的结果来评估一个替代策略可能的价值
Monte Carlo(MC) Off Policy Evaluation
- 目标：在给定由行为策略
π
2
\pi_2
π2产生的轮次(episodes)下，评估策略
π
1
\pi_1
π1的价值
V
π
(
s
)
V^\pi(s)
Vπ(s)
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . . s_1,a_1,r_1,s_2,a_2,r_2,.... s1,a1,r1,s2,a2,r2,....其中的action是由 π 2 \pi_2 π2采样而来
- MDP模型M在策略 π \pi π下产生的收益为 G t = r t + γ r t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . . G_t=r_t+\gamma r_{t+1} + \gamma^2r_{t+2}+\gamma^3r_{t+3}+.... Gt=rt+γrt+1+γ2rt+2+γ3rt+3+....
- 价值函数为 V π ( s ) = E π [ G t ∣ s t = s ] V^\pi(s)=\mathbb{E}_\pi[G_t|s_t = s] Vπ(s)=Eπ[Gt∣st=s]
- 有不同的策略，记为策略 π 2 \pi_2 π2的数据
- 如果 π 2 \pi_2 π2是随机的，那么通常可以使用它来评估一个不同的策略的价值(这是通常情况下遵循的一般原则)
- 再次强调，不需要有模型，也不必要求状态必须是马尔科夫的。
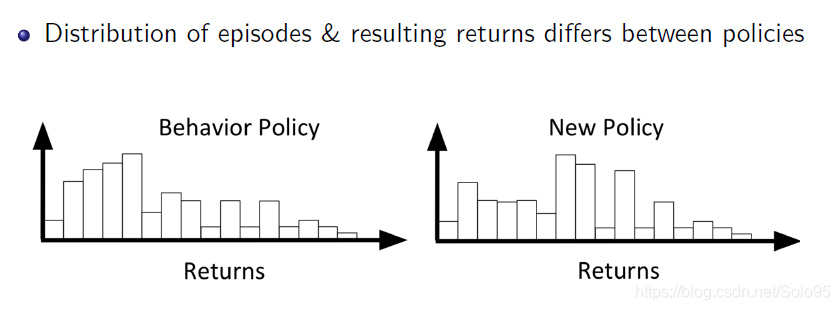
如图，该方法可能面临着已有的行为策略和新的行为策略分布相差巨大的缺点，这点需要注意。
