如何理解动态规划

作者：冒泡
链接：https://www.zhihu.com/question/39948290/answer/83942329
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

如果楼主不是为了竞赛刷题，可以先抛开书本上的什么状态转移方程什么的，可以教你一个民科点的思路O(∩_∩)O：
我们面对的是一个求最优解或统计之类的问题，这个问题基于“我们要模拟完成一个大任务”，这个大任务可以分成若干步骤，每个步骤有若干种决策，每个步骤完成后，就到达了一个阶段性状态
比如，你要从A地到Z地，没有直达，所以第一步需要到一个中间地点，比如H或I，第二步再前进，比如到P或Q，最后到达Z，每一步有若干决策，比如第一步你可以决定到H或I的中的某个，大致就是这样一个模型，可以自己画个地图看看
等等，你大概发现问题了，如果第一步到H和I都可以，第二步到P和Q都可以，那我每一步只选最优，不就用贪心得到结果了吗，没错，如果你需要经历的每个阶段状态跟决策无关，那就贪心得到结果好了，理解贪心了吗：）

然而现实情况可能是，你第一步的选择会影响后面的分支，比如你第一步可以选择到H或I，但是到了H后，你只能选择经过P或Q到Z了，而如果到了I，你只能选择R或S到Z，这样一来，即便第一步到H或I你选择了较好的一条路，也不保证最终结果最优，因为比如你选了H，那万一I-R-Z的路要比H开始到Z的路径短了更多，最优路径可能是A-I-R-Z，所以你要把这些路都尝试一遍，才知道哪个最优，理解穷举了么？：）

OK，我们稍微改下题设，假如从I出发不是到R和S，而是到Q或R，会如何

诚然，我们可以用穷举每条路来解决这个问题，需要穷举的路径数和上面的图一样，但是，我们可以有更快的办法，你不用将A-H-Q-Z和A-I-Q-Z两条路单独计算，因为他们有状态交点，结合第一张图的思想，可以敏锐地感觉到，我们只需要计算到每个有共同状态的位置求各阶段的最优，最后每阶段选最优组合贪心组合起来就行，因为各阶段完成的状态点是大家都有的嘛，因此，咱们先计算A-H-Q和A-I-Q，选个最好的，然后跟Q到Z中最好的拼起来，就是最优了，没必要把所有路径都搞一遍（虽然图里面Q到Z直达，但你可以发挥想象力，将其想象成各种分支的一条复杂道路），这样一来就把一个x^(a+b+c+...)的计算次数降低为x^a+x^b+x^c...，其中x代表每次的决策次数（简单点假设每次决策次数都一样），abc代表每个阶段的步骤数
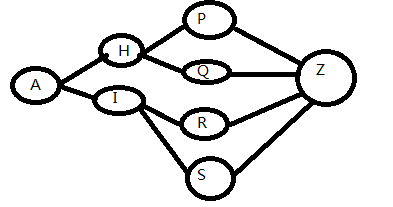
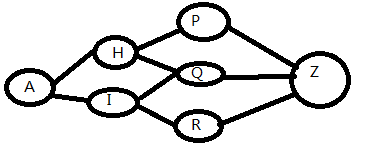
因此，我们可以从A开始，向Z进行BFS，并对BFS中每个点保存最优状态，如果有不同的路径BFS到了同一个点，留最好的一条就行，比如上面这个，你的算法可能先从A-H-Q搜到了Q这个位置，之后从A-I-Q又到了这里，留最好的一条，最后一轮从PQR三个点到Z，就结束了，相对第二章图要少一次运算
如果你理解了，恭喜你已经能有效解决很多需要DP的问题了，同时还学会了解图论的单源最短路径问题呢

 

最后用经典的0-1背包问题做个例子，巩固一下吧，这个任务是，我们从N个物品选若干塞到可以承受最大重量W的包包里面，要价值最大，因此就可以将任务分成N个步骤，每个步骤面对第i号物品，决策有两条：选，还是放弃，这里的状态，就是影响之后步骤决策的因素，在这里，就是“背包的剩余空间”
比如，物品的重量是1,2,3,4,5,6，W=12，从头决策，0表示放弃，1表示选，BFS三次后有八种状态：
000 剩12
001 剩9
……（略）
110 剩9
……（略）
前三次步骤后，001和110到达了同样的状态，都是剩余可装重量9的东西，这样在剩下的决策中，这俩分支走的路都是一样的，跟你之前是选了001还是110没有任何关系（无后效性），因此只要看001价值大，还是110价值大就可以了，8个状态减少为7个，继续BFS下去，每一轮都合并同样状态，完成后，从最后一轮的所有状态中，找到价值最大的就ok了
由于状态最多有W+1个，进行N轮，因此复杂度O(NW)，书上说的状态迁移方程的办法其实跟这个过程很类似，不过对于有些题目，比起BFS+状态合并，状态方程的分析可以做更好的优化，如引入单调队列什么的，但BFS+状态合并可以让你得到一个没有追求极限但是也比较快的解决方案了，结合具体问题有时候更适合，比如根据问题的实际需求，搜索可以限界剪枝减少工作量，我在工作中就用过，替换了同事从wiki抄的DP算法，效率能提升一些

============我是补充的分割线====================

下午由于上班，写得比较仓促，已经有同学指出我的思路其实就是将问题转换为图中求路径，的确是这样的，这个做法虽然很多时候比教科书的状态转移方程做法稍慢，但一招就能覆盖很多问题，比如下面三道：
Problem 81 - Project Euler
Problem 82 - Project Euler
Problem 83 - Project Euler
这三道题都是走矩阵，要求走过的节点的值的和最小，81是只能往右和往下，一眼就是DP，82是可以上下右，可以按列DP，83是上下左右都可以，就用不上DP了，然而用单源最短路径可以通杀
因为我从开始学算法就很懒，总是追求最少的招数解决尽量多的问题，在复杂度达到了也不太会尽量追求更快，所以ACM被虐很惨，刷题请慎用，也请OJ大神们轻拍：）

可能关于“状态是怎么决定的”这个问题上面描述比较简略，就再补充一下，其实就是可能影响下一个步骤决策的因素，都是当前状态，比如上面的01背包，每次的决策是选或不选，但是如果剩余W已经不够了，就只剩下“不选”一条决策可用了，因此用剩余W来做状态
再比如这题：
Problem 191 - Project Euler
抽象后其实是说：一个由L、O、A组成的长度为30的字符串，不能出现连续3个或以上的A，最多出现一个L，有多少个这样的字符串？
很明显需要30步决策，每次决策时候要从3个字母里面选合法的，O任何情况都合法，L在没出现过的情况下合法，A则在现有串最后不是AA时候合法，因此状态就是是否出现过L和最后两个字母中A的分布情况的一个组合，L是否出现有两个值，A的分布有**，A*，*A，AA四种（*代表O或L，不用展开了），所以就是2*4=8种状态啦

最后留个小题，是以前做考官时候经常用的一道面试题，印象中有算法基础的同学六七成都能立即说“用DP”，然而一问状态转移就晕了^_^：
在约定的规则下，以数字数组的形式输入一手斗地主的牌，设计算法计算这手牌最少几把可以出完
注意这里只是用斗地主做个例子，不代表牌数限制为20张，可以看做是一个N个数字根据规则分组的问题，说斗地主是因为之前是做游戏行业的，而且面试时候这样说比较容易降低同学们的紧张度，同时也是一个暗示：大家都知道斗地主靠贪心法是得不到最优出牌顺序的吧，哈。。。